Two-dimensional nonlinear frequency converters A Arie A Bahabad

Two-dimensional nonlinear frequency converters A. Arie, A. Bahabad, Y. Glickman, E. Winebrand, D. Kasimov and G. Rosenman Dept. of Physical Electronics, School of Electrical Engineering Tel-Aviv University, Tel-Aviv, Israel FRISNO 8, Ein Bokek 2005 1

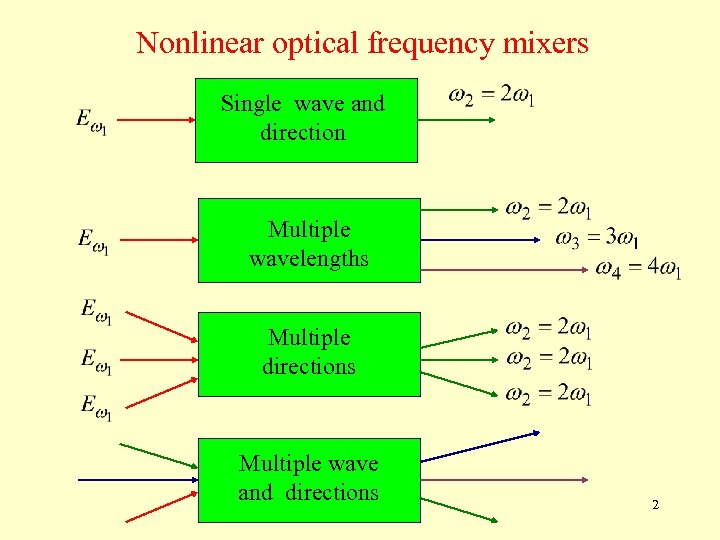
Nonlinear optical frequency mixers Single wave and direction Multiple wavelengths Multiple directions Multiple wave and directions 2

Questions about Nonlinear Mixers 1. How to design them? 1. Single wave and direction: 1 D periodic modulation of c(2). 2. Multiple wave, single direction: 1 D quasi-periodic modulation. 3. Multiple waves and directions: 2 D periodic and quasi-periodic modulation of c(2). Design using Dual Grid Method 2. 2. How to produce them? 3. Domain reversal in ferroelectrics (Li. NBO 3, KTP, RTP) using electric field: 4. Through planar electrodes 5. High voltage atomic force microscope (sub-micron resolution) 6. Electron beam poling 7. 3. What can we do with them? 3

Electric field poling of ferroelectric crystals Technological mature, Commercially available Limited resolution (>4 m), long processing time. M. Yamada et al, Applied Phys. Lett. 62, 435 (1993) G. Rosenman et al, Phys. Rev. Lett. 73, 3650 (1998) 4

High Voltage Atomic Force Microscope Poling Rb. Ti. OPO 4 High Voltage AFM Cantilever Laser DV~15 k. V Ferroelectric Sample Scanner 590 nm Order of magnitude improvement in poling resolution. Main technological problem: writing time (1 week (!) for 1 mm 150 m sample) Y. Rosenwaks, G. Rosenman, TAU Applied Phys. Lett. 82, 103 (2003) Phys. Rev. Lett. 90, 107601 (2003) 5

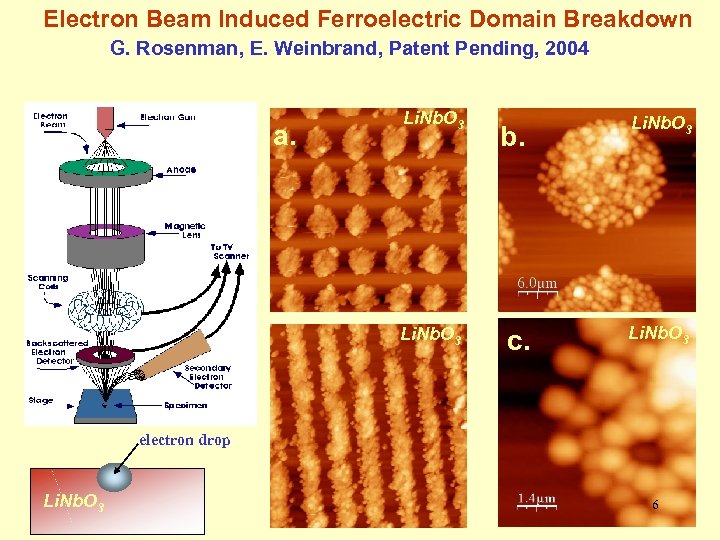
Electron Beam Induced Ferroelectric Domain Breakdown G. Rosenman, E. Weinbrand, Patent Pending, 2004 a. Li. Nb. O 3 b. Li. Nb. O 3 c. Li. Nb. O 3 electron drop Li. Nb. O 3 6

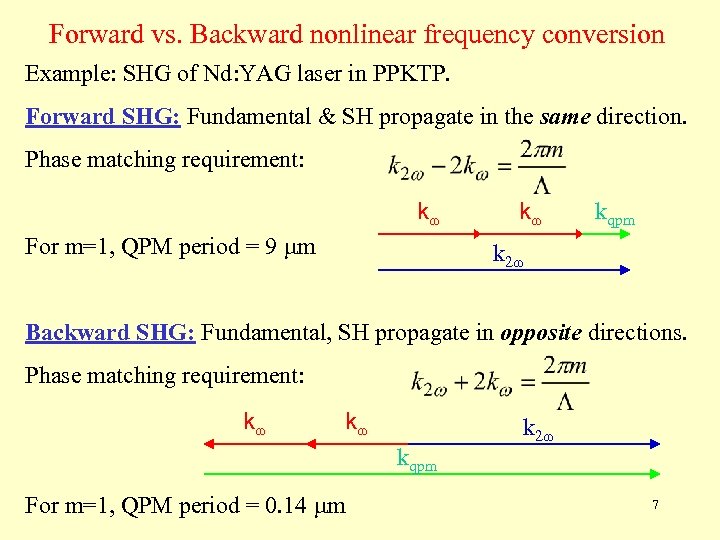
Forward vs. Backward nonlinear frequency conversion Example: SHG of Nd: YAG laser in PPKTP. Forward SHG: Fundamental & SH propagate in the same direction. Phase matching requirement: k For m=1, QPM period = 9 m k kqpm k 2 Backward SHG: Fundamental, SH propagate in opposite directions. Phase matching requirement: k k kqpm For m=1, QPM period = 0. 14 m k 2 7

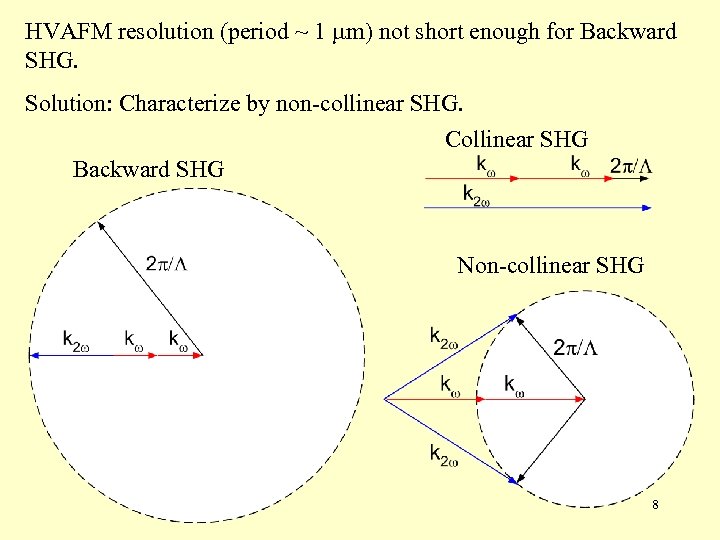
HVAFM resolution (period ~ 1 m) not short enough for Backward SHG. Solution: Characterize by non-collinear SHG. Collinear SHG Backward SHG Non-collinear SHG 8

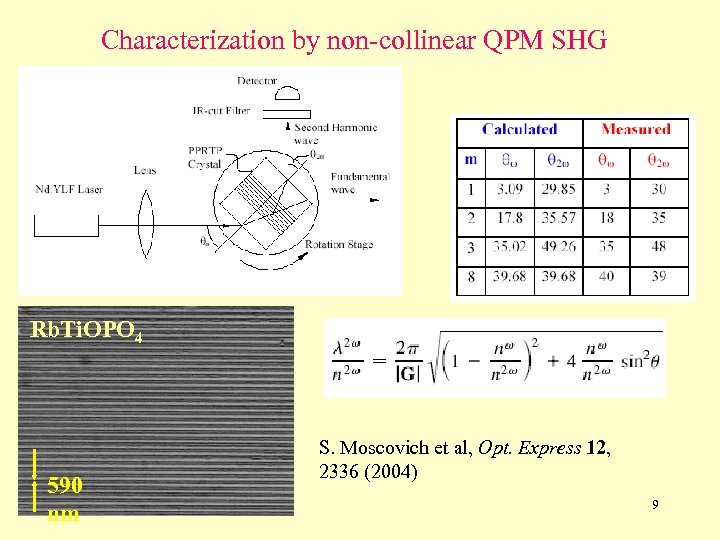
Characterization by non-collinear QPM SHG Rb. Ti. OPO 4 590 nm S. Moscovich et al, Opt. Express 12, 2336 (2004) 9

Multiple-wavelength QPM nonlinear interactions • Examples of multiple interactions using the 2 nd-order nonlinear coefficient, d(z): – Dual wavelength SHG, w 1 2 w 1 , w 2 2 w 2 – Frequency tripling, w 1 3 w 1 [ SHG: w 1 2 w 1 + SFG: w 1 + 2 w 1 3 w 1 ] All optical splitting and all-optical deflection • Aperiodic modulation of the nonlinear coefficient is required in order to obtain high efficiency simultaneously for two different processes. • Suggested solution: quasi-periodic modulation of the nonlinear coefficient. K. Fradkin-Kashi and A. Arie, IEEE J. Quantum Electron. 35, 1649 (1999). 10

Quasi-periodic structures (QPS) • Quasi-periodic patterns found in nature, e. g. quasicrystals and studied by mathematicians (Fibonacci) and crystalographers. • A quasi-periodic structure can support more than one spatial frequency. The Fourier transform of onedimensional QPS has peaks at spatial frequencies: - m, n integers. - Note: Two characteristic frequencies. D. Schetman et al. , Phys. Rev. Lett. 53, 195 (1984). 11

$Quasi-crystals in nature Scanning electron micrographs of single grains of quasicrystals Typical diffraction diagram$

Quasi-crystals in nature Scanning electron micrographs of single grains of quasicrystals Typical diffraction diagram of a quasicrystal, exhibiting 5 -fold or 10 -fold rotational symmetry 12

Quasi-periodic structures (QPS) cont. • Nonlinear optics: building blocks ferroelectric domains with different widths and reversed polarization. • Order of blocks quasi-periodic series {zn}: - E. g. Fibonacci series: 8 LSLSL • Fourier transform has peaks at spatial frequencies: ; - m, n integers; irrational. - Note: Two characteristic frequencies. (average lattice parameter) 13

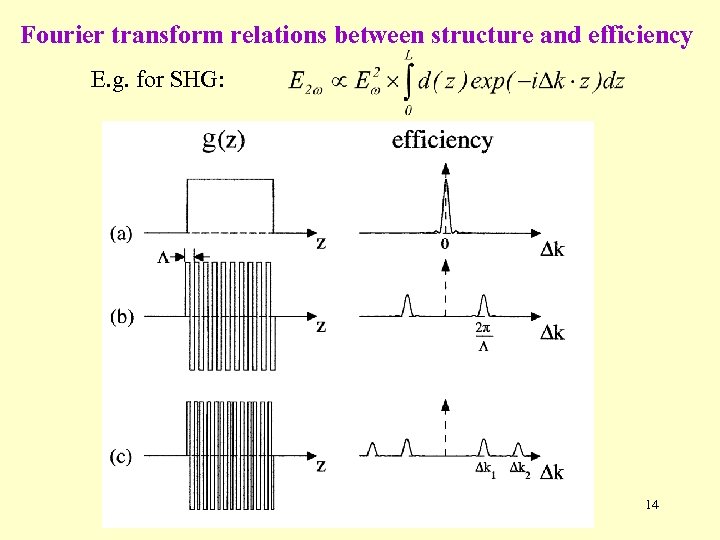
Fourier transform relations between structure and efficiency E. g. for SHG: 14

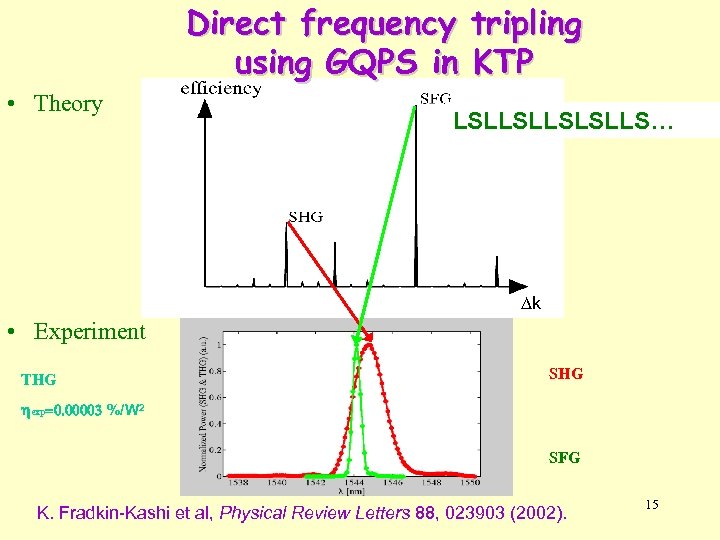
Direct frequency tripling using GQPS in KTP • Theory LSLLSLLS… k • Experiment THG SHG hexp=0. 00003 %/W 2 SFG K. Fradkin-Kashi et al, Physical Review Letters 88, 023903 (2002). 15

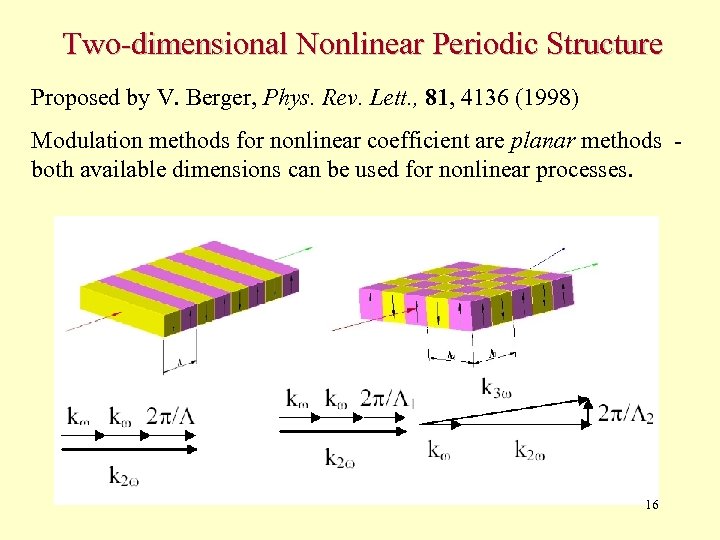
Two-dimensional Nonlinear Periodic Structure Proposed by V. Berger, Phys. Rev. Lett. , 81, 4136 (1998) Modulation methods for nonlinear coefficient are planar methods both available dimensions can be used for nonlinear processes. 16

2 D Periodic Lattices 2 D Real Lattice: A set of points at locations Where m, n are integers, and a 1, a 2 are (primitive) translation vectors. There are 5 Bravais lattices in 2 D Examples: Square lattice: Hexagonal lattice: 2 D Lattice + basis (atoms) => 2 D Lattice + basis (nonlinear domain) => Crystal Nonlinear superlattice 17

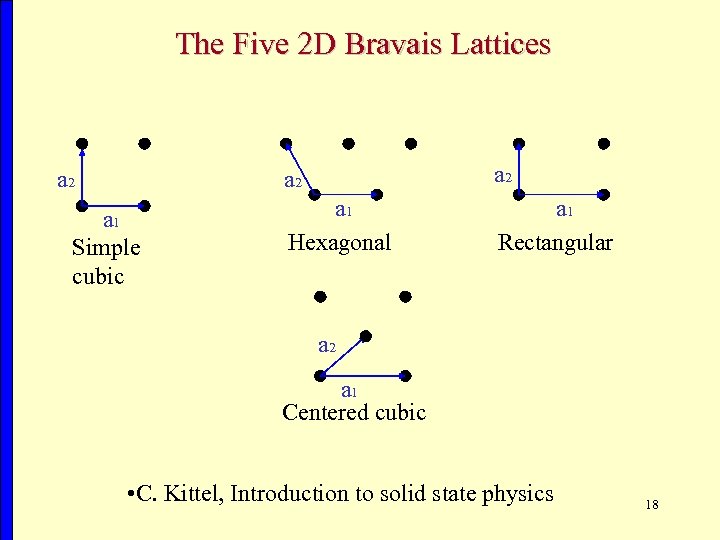
The Five 2 D Bravais Lattices a 2 a 1 Simple cubic a 2 a 1 Hexagonal a 1 Rectangular a 2 a 1 Centered cubic • C. Kittel, Introduction to solid state physics 18

The Reciprocal Lattice Define primitive b 1, b 2, vectors of the Reciprocal Lattice such that The Reciprocal Lattice points are given by In crystals, the Reciprocal Lattice is identical to a scaled version of the diffraction pattern of the crystal. The nonlinear susceptibility can be written as a Fourier series in the Reciprocal Lattice: E. g. , for hexagonal lattice of cylinders (with circle filling factor f), 19

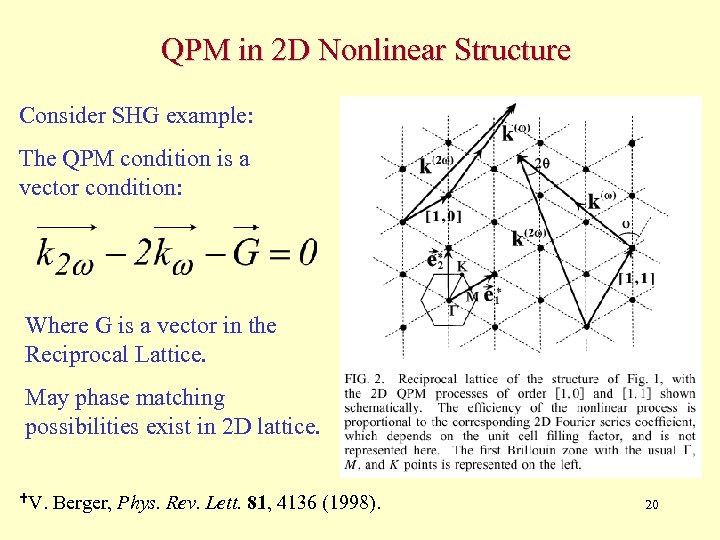
QPM in 2 D Nonlinear Structure Consider SHG example: The QPM condition is a vector condition: Where G is a vector in the Reciprocal Lattice. May phase matching possibilities exist in 2 D lattice. V. Berger, Phys. Rev. Lett. 81, 4136 (1998). 20

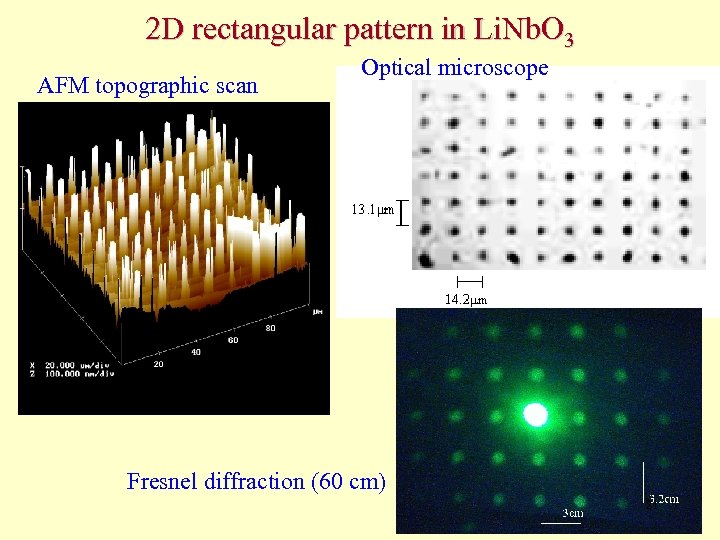
2 D rectangular pattern in Li. Nb. O 3 AFM topographic scan Optical microscope Fresnel diffraction (60 cm) 21

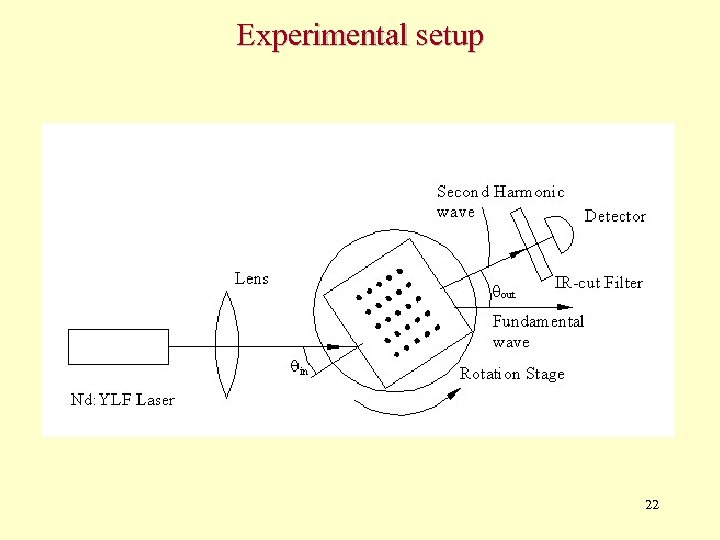
Experimental setup 22

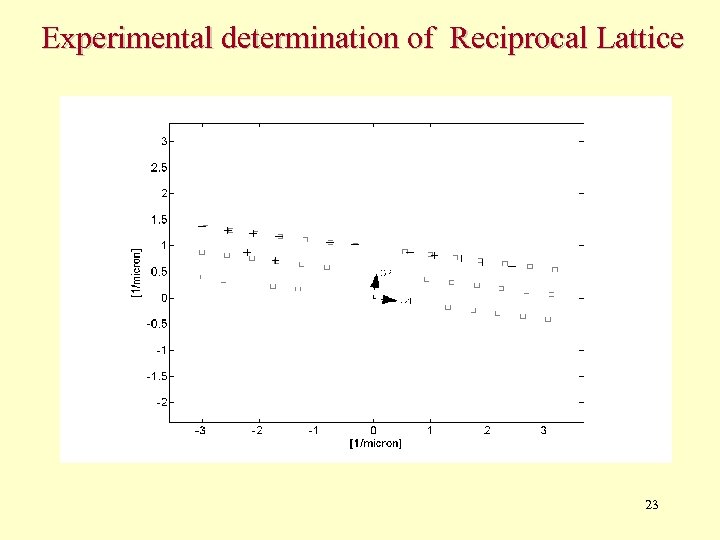
Experimental determination of Reciprocal Lattice 23

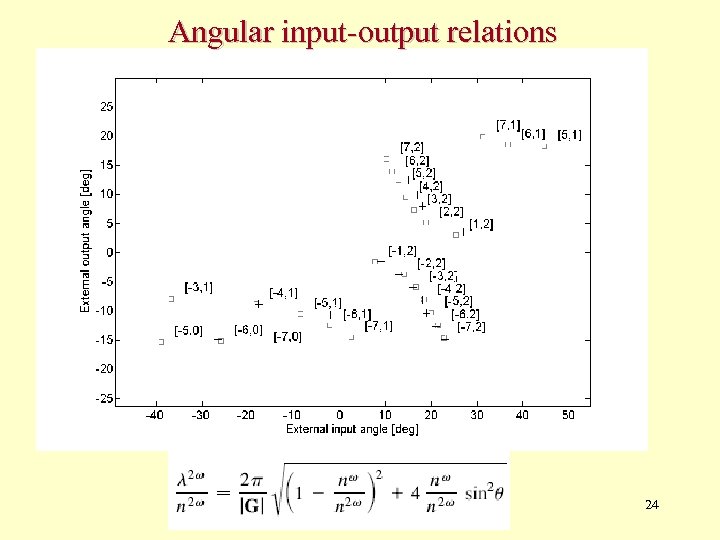
Angular input-output relations 24

2 D QPM structures with annular symmetry An annular structure with period ~ 25 microns ~ 800 micron ~ 1 mm 25

Geometrical considerations Phase matching can occur at all directions. Different processes can be phase matched at different angles. We can calculate the angle of the second harmonic using the law of cosines. 26

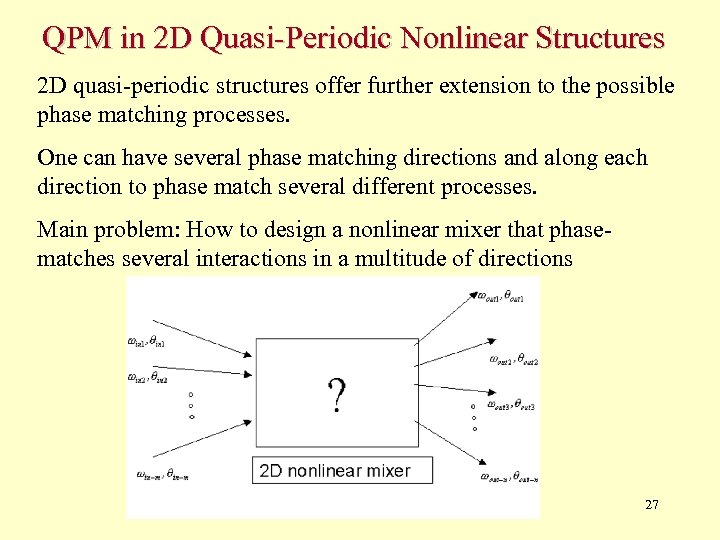
QPM in 2 D Quasi-Periodic Nonlinear Structures 2 D quasi-periodic structures offer further extension to the possible phase matching processes. One can have several phase matching directions and along each direction to phase match several different processes. Main problem: How to design a nonlinear mixer that phasematches several interactions in a multitude of directions 27

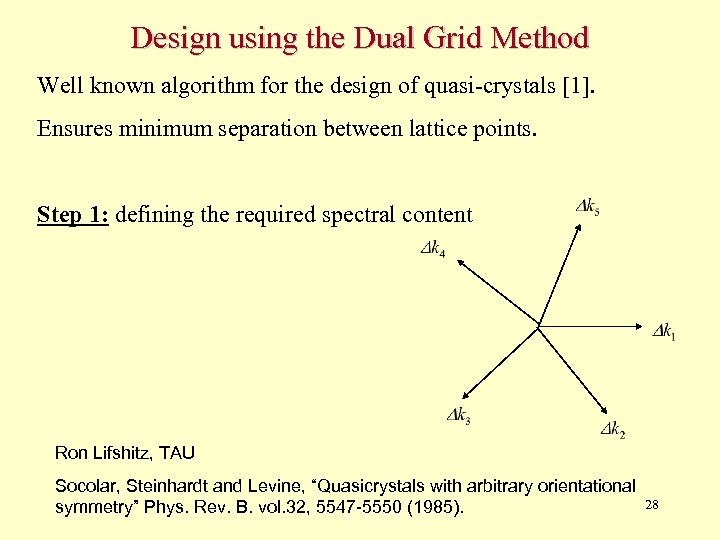
Design using the Dual Grid Method Well known algorithm for the design of quasi-crystals [1]. Ensures minimum separation between lattice points. Step 1: defining the required spectral content Ron Lifshitz, TAU Socolar, Steinhardt and Levine, “Quasicrystals with arbitrary orientational symmetry” Phys. Rev. B. vol. 32, 5547 -5550 (1985). 28

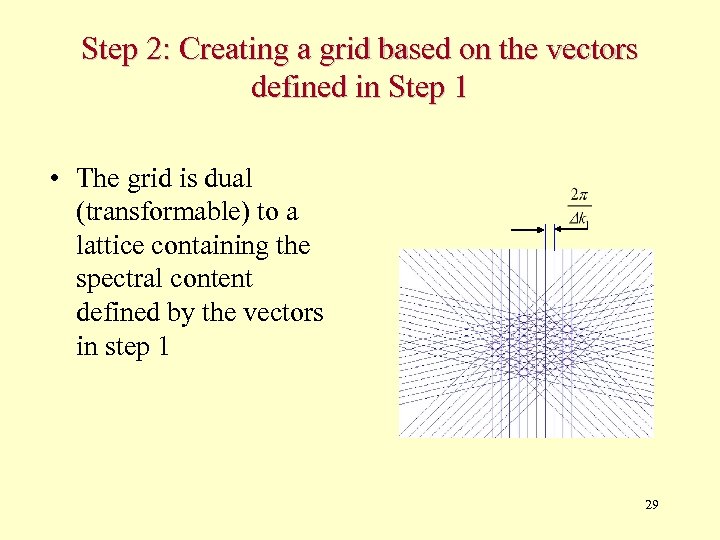
Step 2: Creating a grid based on the vectors defined in Step 1 • The grid is dual (transformable) to a lattice containing the spectral content defined by the vectors in step 1 29

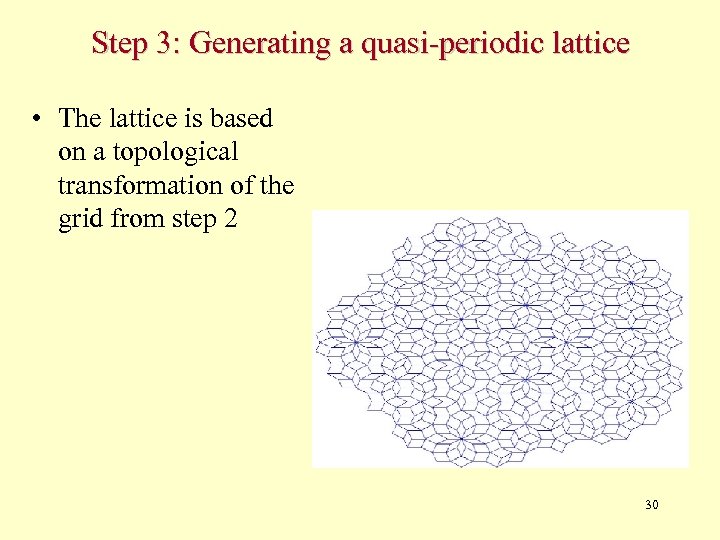
Step 3: Generating a quasi-periodic lattice • The lattice is based on a topological transformation of the grid from step 2 30

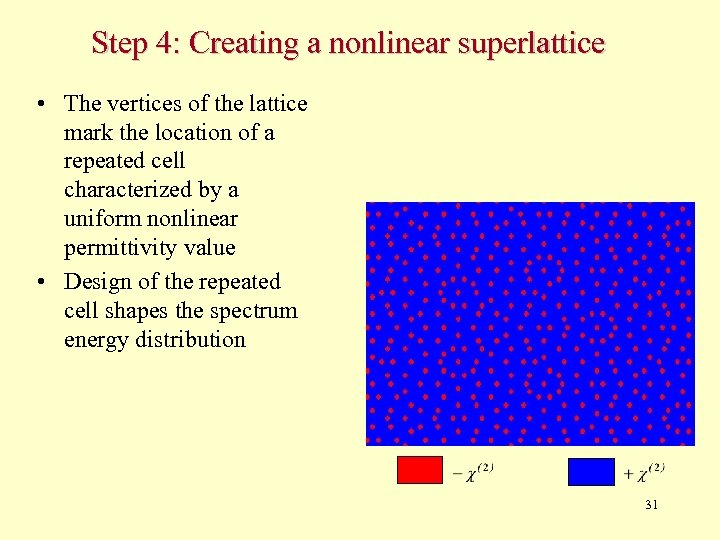
Step 4: Creating a nonlinear superlattice • The vertices of the lattice mark the location of a repeated cell characterized by a uniform nonlinear permittivity value • Design of the repeated cell shapes the spectrum energy distribution 31

How to construct the quasi-crystal? 1. Start with D two-dimensional mismatch vectors 2. Add D-2 components to each of the mismatch vectors 3. One obtains D D-dimensional vectors 4. Find the dual basis , where a is twodimensional and b is D-2 dimensional, such that 5. Put a cell at a subset of the positions given 32

DGM design example in 1 D: Quasi-periodic superlattice • Choosing required spectral content – e. g. two parallel phase-mismatch vectors. 33

Step 2: Creating a 1 D grid • Creating the grid: each vector defines a family of lines in the direction of the vector and with separation inversely proportional to its magnitude 34

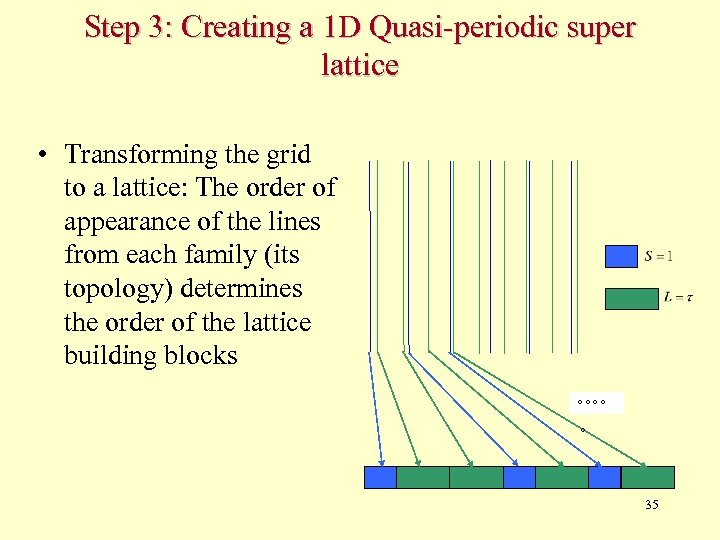
Step 3: Creating a 1 D Quasi-periodic super lattice • Transforming the grid to a lattice: The order of appearance of the lines from each family (its topology) determines the order of the lattice building blocks 35

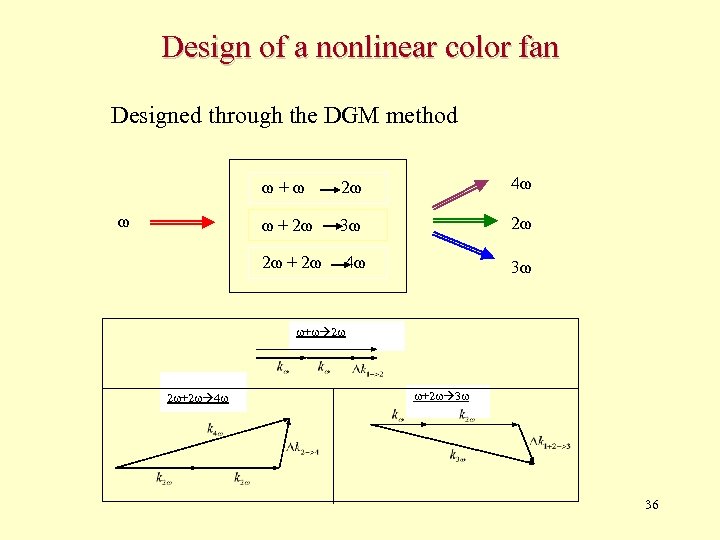
Design of a nonlinear color fan Designed through the DGM method ω+ω 4ω ω + 2ω 3ω 2ω 2ω + 2ω ω 2ω 4ω 3ω + 2 2 +2 4 +2 3 36

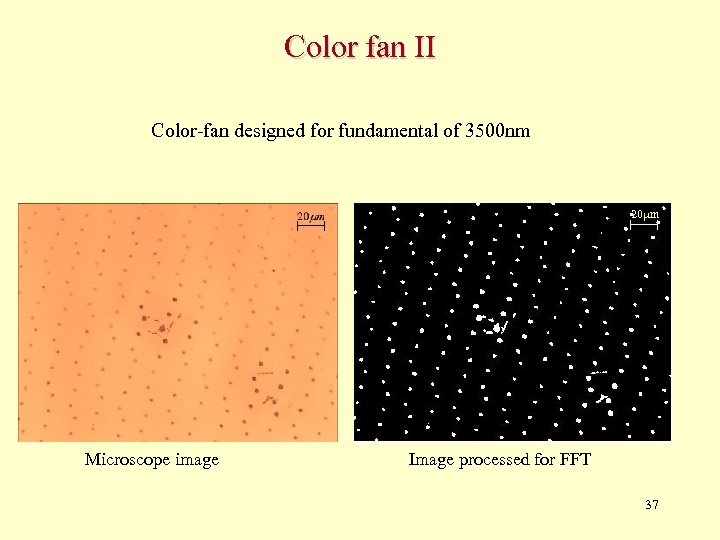
Color fan II Color-fan designed for fundamental of 3500 nm 20 m Microscope image Image processed for FFT 37

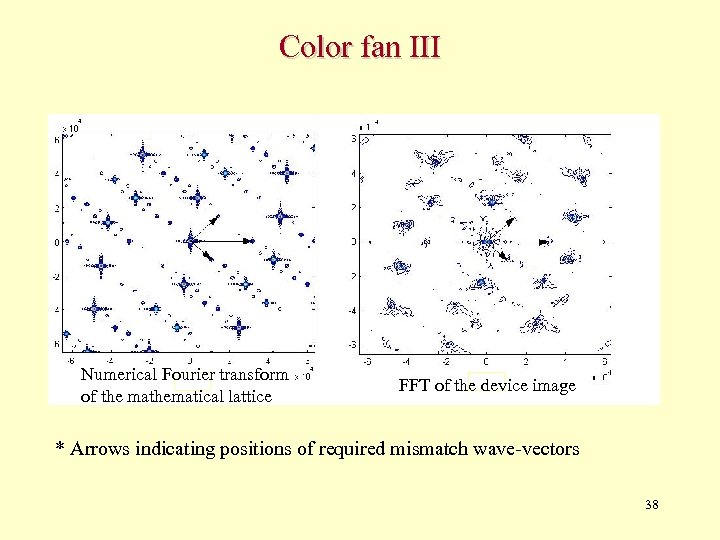
Color fan III Numerical Fourier transform of the mathematical lattice FFT of the device image * Arrows indicating positions of required mismatch wave-vectors 38

$Color fan IV Diffraction Image 39$

Color fan IV Diffraction Image 39

Phase-matching methods and corresponding conditions on wavevector difference 1. J. A. Giordmaine, Phys. Rev. Lett. 8, 19 (1962); P. D. Maker et al. , 8, 21 (1962). 2. J. A. Armstrong et al. , Phys. Rev. 127, 1918 (1962). 3. S. -N. Zhu et al. , Science 278, 843 (1997), K. Fradkin-Kashi and A. Arie, IEEE J. Quantum Electron. 35, 1649 (1999). 4. V. Berger, Phys. Rev. Lett. 81 4136 (1998). 40

Nonlinear devices utilizing multiple phase matching possibilities 1. Ring cavity mixers 2. Multiple harmonic generators 3. Nonlinear prisms and color fans 4. Omni-directional mixers 5. All-optical deflectors and splitters 41

Nonlinear deflection and nonlinear splitting All-optical deflection of wy as a function of pump wz. Step 1: collinear SHG of pump: z+ z =>(2 )z Step 2: noncollinear DFG of SH and cross polarized input signal (2 ) z- y =>noncollinear y at angle q with respect to input beam. All-optical splitting of wy into two directions Step 1: collinear SHG of pump: z+ z =>(2 )z (same as above) Step 2: Simultaneous noncollinear DFG of SH and cross polarized input signal into two different directions S. M. Saltiel and Y. S. Kivshar, Opt. Lett. 27, 921 (2002). 42

All-optical deflection & splitting Saltiel and Kivshar, Opt. Lett. 27, 921 (2002) 43

Summary • New methods for poling ferroelectrics offer improved resolution and larger design flexibility: – Sub-micron resolution using HVAFM poling. Characterized by non-collinear SHG. – Modified E-beam poling. Characterized by 2 D NLO • Design & fabrication of a 1 D quasi-periodic structure for multiple-wavelength nonlinear interactions. –Phase-match any two arbitrarily chosen interactions. –Dual wavelength SHG and frequency tripling demonstrated in KTP. • Multiple-wavelength interactions by 2 D periodic nonlinear structures. – 15 different phase matching options measured in 2 D rectangular pattern. –Annular symmetry device recently realized • Further extension by 2 D quasi-periodic structures –Dual grid method offer a possibility to phase match several interactions in a multitude of directions. • Next steps: experimental realizations, demonstration of devices, finding 44 useful applications.