4b542d582763b043fc2603bb643e9ce7.ppt
- Количество слайдов: 87

Tutorial on Bayesian Networks Jack Breese Daphne Koller Microsoft Research Stanford University breese@microsoft. com koller@cs. stanford. edu First given as a AAAI’ 97 tutorial. 1

Probabilities n Probability distribution P(X|x) u. X is a random variable n Discrete n Continuous u x is background state of information © Jack Breese (Microsoft) & Daphne Koller (Stanford) 7

Discrete Random Variables n Finite set of possible outcomes X binary: © Jack Breese (Microsoft) & Daphne Koller (Stanford) 8

Continuous Random Variable n Probability distribution (density function) over continuous values 5 © Jack Breese (Microsoft) & Daphne Koller (Stanford) 7 9

Bayesian networks n Basics u Structured representation u Conditional independence u Naïve Bayes model u Independence facts © Jack Breese (Microsoft) & Daphne Koller (Stanford) 14
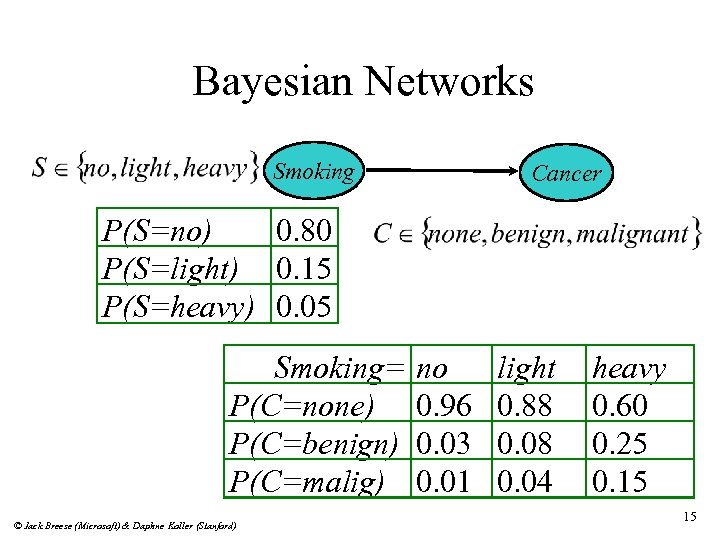
Bayesian Networks Smoking Cancer P(S=no) 0. 80 P(S=light) 0. 15 P(S=heavy) 0. 05 Smoking= P(C=none) P(C=benign) P(C=malig) © Jack Breese (Microsoft) & Daphne Koller (Stanford) no 0. 96 0. 03 0. 01 light 0. 88 0. 04 heavy 0. 60 0. 25 0. 15 15
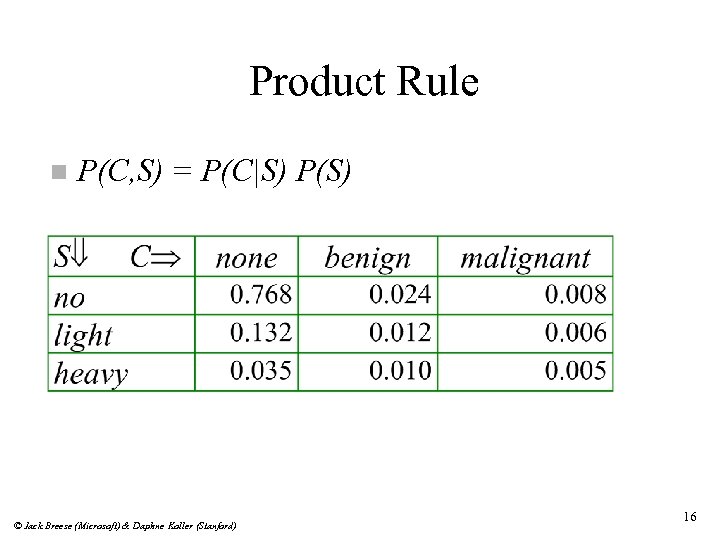
Product Rule n P(C, S) = P(C|S) P(S) © Jack Breese (Microsoft) & Daphne Koller (Stanford) 16
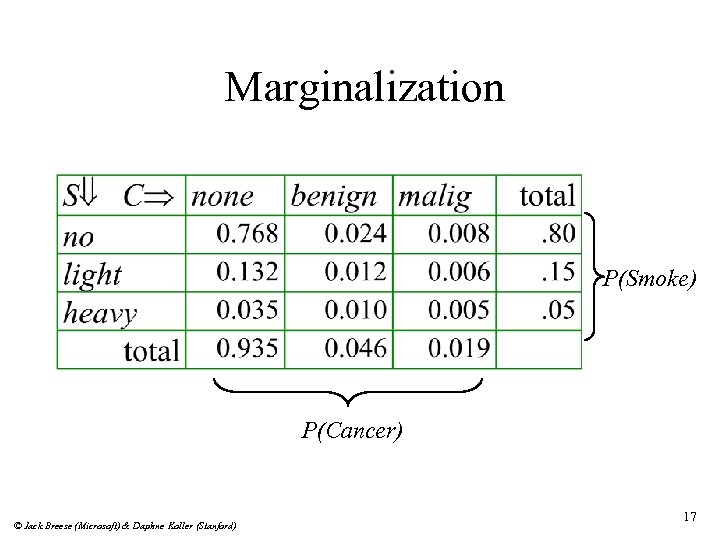
Marginalization P(Smoke) P(Cancer) © Jack Breese (Microsoft) & Daphne Koller (Stanford) 17
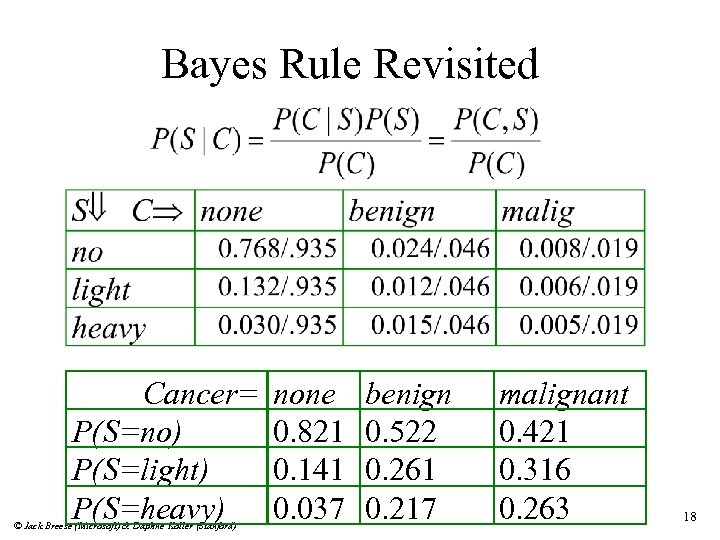
Bayes Rule Revisited Cancer= P(S=no) P(S=light) P(S=heavy) © Jack Breese (Microsoft) & Daphne Koller (Stanford) none 0. 821 0. 141 0. 037 benign 0. 522 0. 261 0. 217 malignant 0. 421 0. 316 0. 263 18
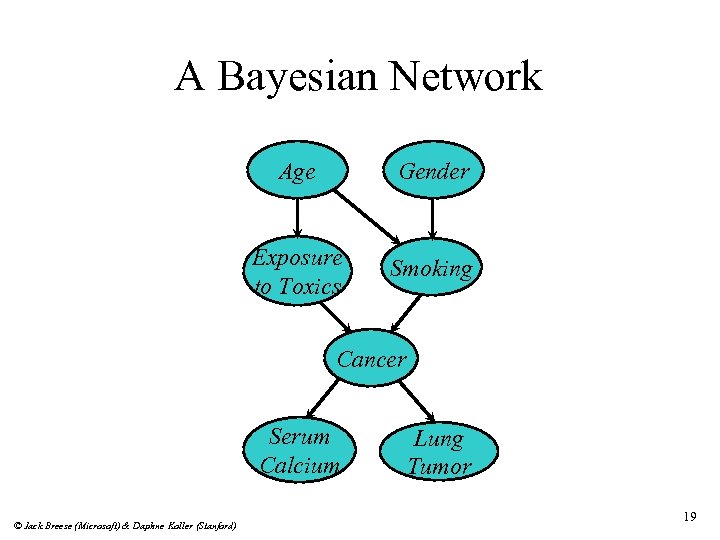
A Bayesian Network Age Gender Exposure to Toxics Smoking Cancer Serum Calcium © Jack Breese (Microsoft) & Daphne Koller (Stanford) Lung Tumor 19
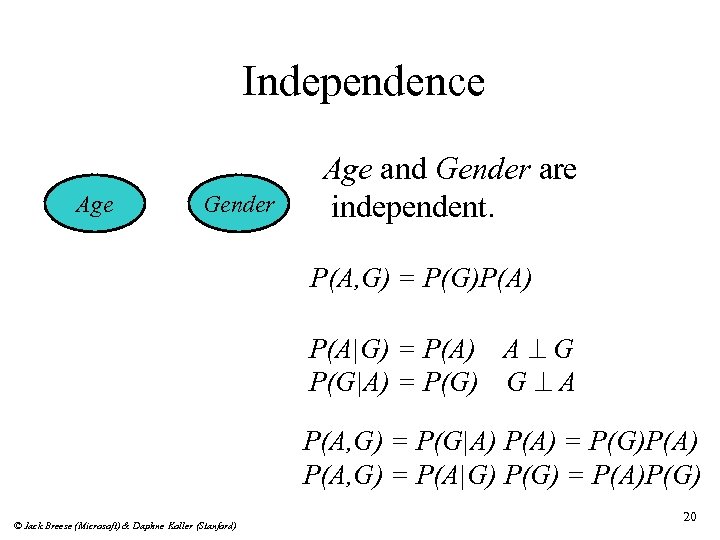
Independence Age Gender Age and Gender are independent. P(A, G) = P(G)P(A) P(A|G) = P(A) A ^ G P(G|A) = P(G) G ^ A P(A, G) = P(G|A) P(A) = P(G)P(A) P(A, G) = P(A|G) P(G) = P(A)P(G) © Jack Breese (Microsoft) & Daphne Koller (Stanford) 20
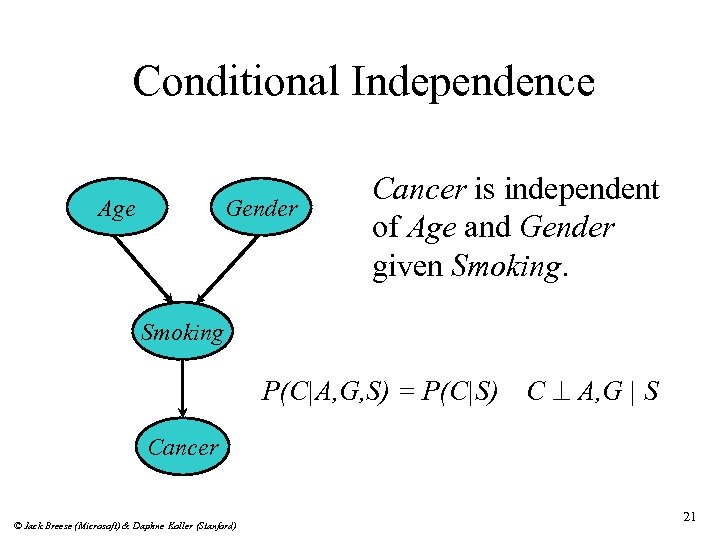
Conditional Independence Age Gender Cancer is independent of Age and Gender given Smoking P(C|A, G, S) = P(C|S) C ^ A, G | S Cancer © Jack Breese (Microsoft) & Daphne Koller (Stanford) 21

More Conditional Independence: Naïve Bayes Serum Calcium and Lung Tumor are dependent Cancer Serum Calcium © Jack Breese (Microsoft) & Daphne Koller (Stanford) Serum Calcium is independent of Lung Tumor, given Cancer Lung Tumor P(L|SC, C) = P(L|C) 22
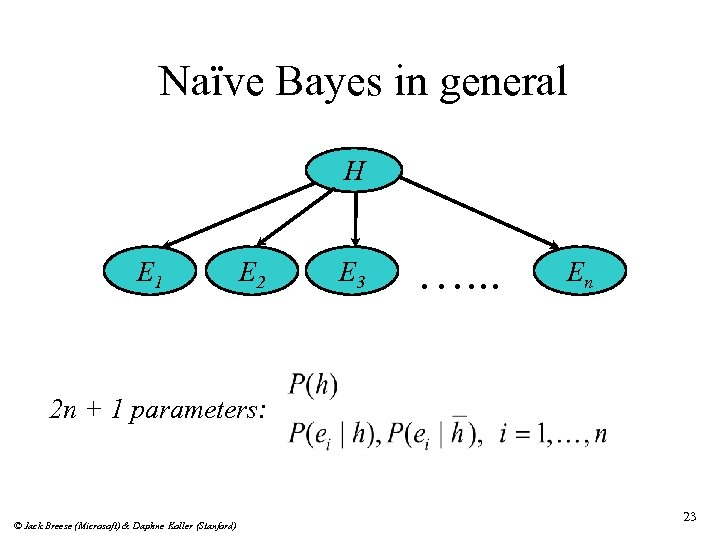
Naïve Bayes in general H E 1 E 2 E 3 …. . . En 2 n + 1 parameters: © Jack Breese (Microsoft) & Daphne Koller (Stanford) 23
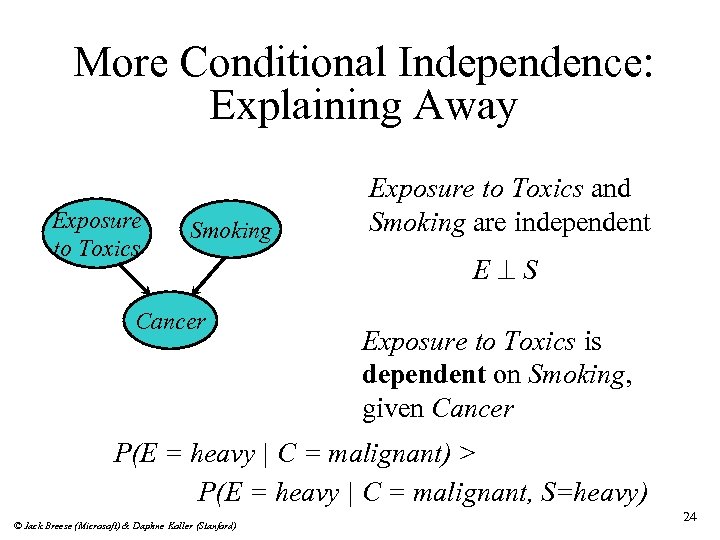
More Conditional Independence: Explaining Away Exposure to Toxics Smoking Cancer Exposure to Toxics and Smoking are independent E^S Exposure to Toxics is dependent on Smoking, given Cancer P(E = heavy | C = malignant) > P(E = heavy | C = malignant, S=heavy) © Jack Breese (Microsoft) & Daphne Koller (Stanford) 24
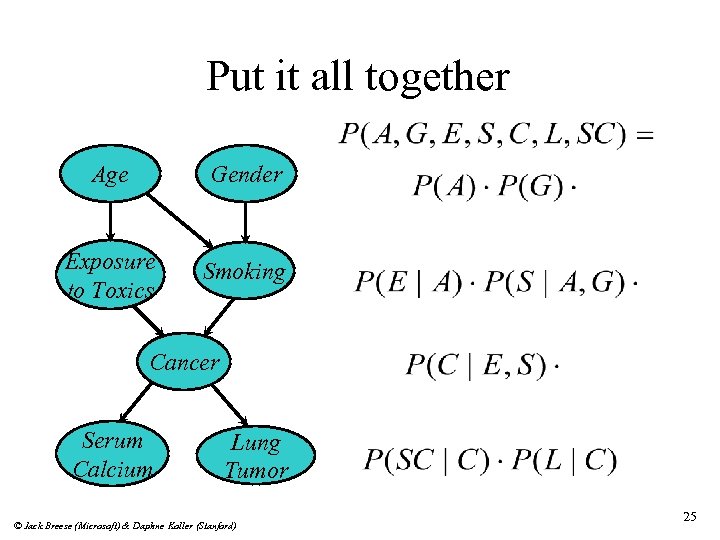
Put it all together Age Gender Exposure to Toxics Smoking Cancer Serum Calcium Lung Tumor © Jack Breese (Microsoft) & Daphne Koller (Stanford) 25

General Product (Chain) Rule for Bayesian Networks Pai=parents(Xi) © Jack Breese (Microsoft) & Daphne Koller (Stanford) 26
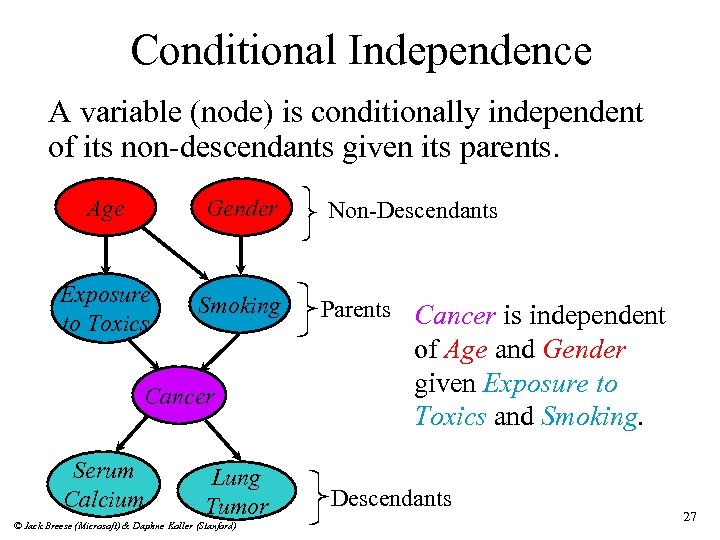
Conditional Independence A variable (node) is conditionally independent of its non-descendants given its parents. Age Gender Exposure to Toxics Smoking Cancer Serum Calcium Lung Tumor © Jack Breese (Microsoft) & Daphne Koller (Stanford) Non-Descendants Parents Cancer is independent of Age and Gender given Exposure to Toxics and Smoking. Descendants 27
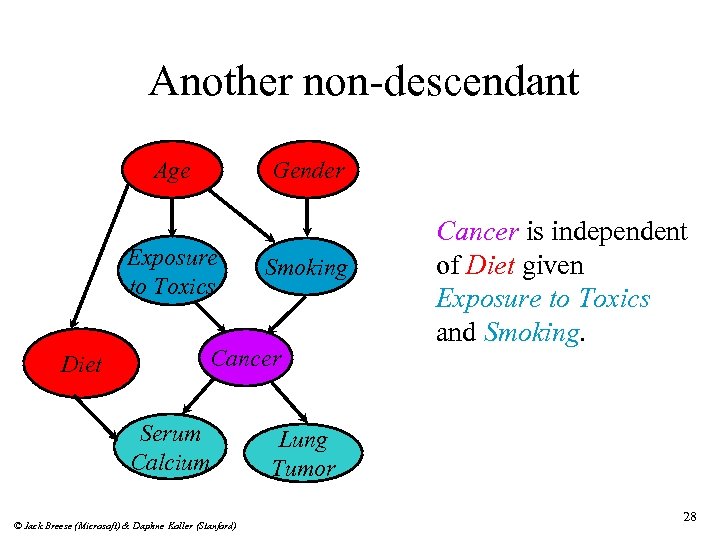
Another non-descendant Age Gender Exposure to Toxics Diet Smoking Cancer Serum Calcium © Jack Breese (Microsoft) & Daphne Koller (Stanford) Cancer is independent of Diet given Exposure to Toxics and Smoking. Lung Tumor 28

Independence and Graph Separation Given a set of observations, is one set of variables dependent on another set? n Observing effects can induce dependencies. n d-separation (Pearl 1988) allows us to check conditional independence graphically. n © Jack Breese (Microsoft) & Daphne Koller (Stanford) 29

CPCS Network © Jack Breese (Microsoft) & Daphne Koller (Stanford) 36
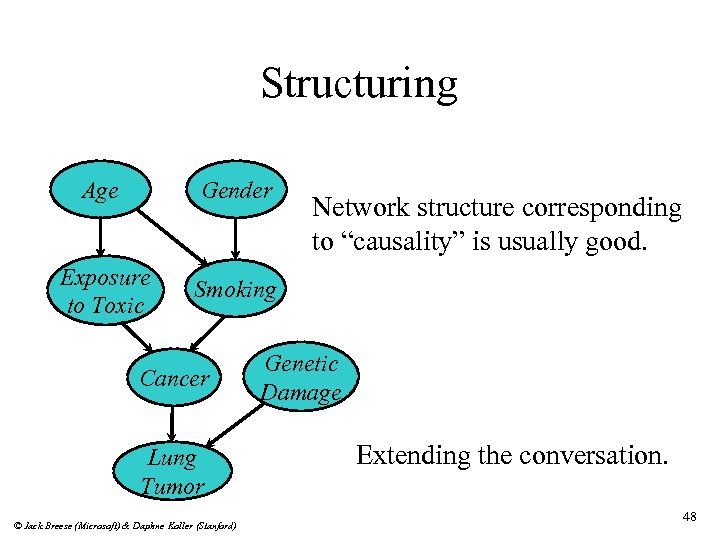
Structuring Age Gender Exposure to Toxic Smoking Cancer Lung Tumor © Jack Breese (Microsoft) & Daphne Koller (Stanford) Network structure corresponding to “causality” is usually good. Genetic Damage Extending the conversation. 48
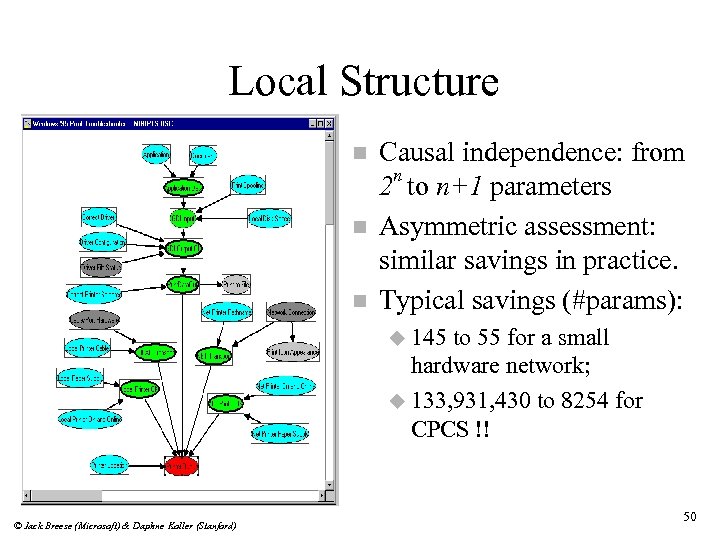
Local Structure n n n Causal independence: from 2 n to n+1 parameters Asymmetric assessment: similar savings in practice. Typical savings (#params): u 145 to 55 for a small hardware network; u 133, 931, 430 to 8254 for CPCS !! © Jack Breese (Microsoft) & Daphne Koller (Stanford) 50

Course Contents Concepts in Probability n Bayesian Networks » Inference n Decision making n Learning networks from data n Reasoning over time n Applications n © Jack Breese (Microsoft) & Daphne Koller (Stanford) 51

Inference Patterns of reasoning n Basic inference n Exact inference n Exploiting structure n Approximate inference n © Jack Breese (Microsoft) & Daphne Koller (Stanford) 52
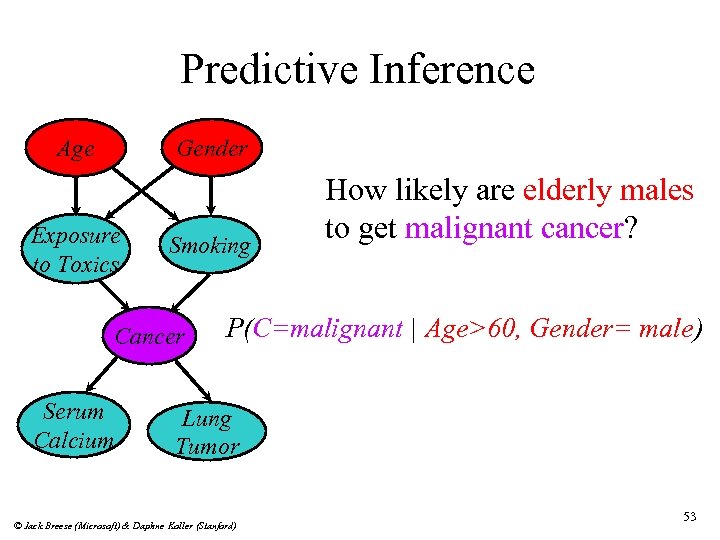
Predictive Inference Age Gender Exposure to Toxics Smoking Cancer Serum Calcium How likely are elderly males to get malignant cancer? P(C=malignant | Age>60, Gender= male) Lung Tumor © Jack Breese (Microsoft) & Daphne Koller (Stanford) 53
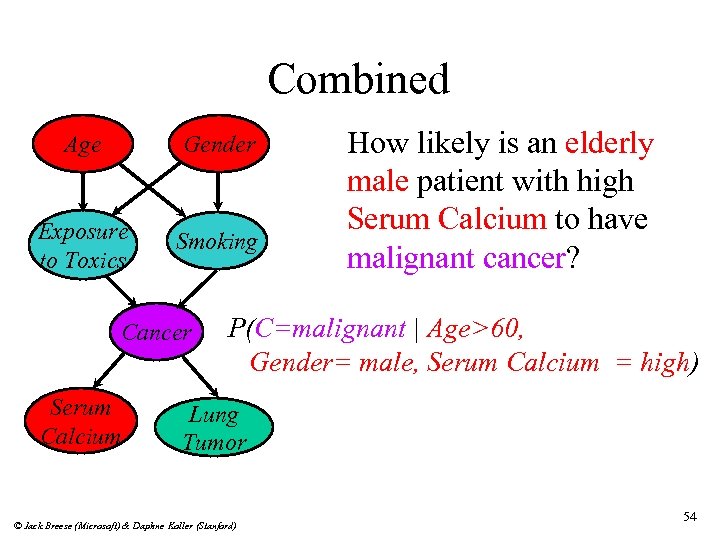
Combined Age Gender Exposure to Toxics Smoking Cancer Serum Calcium How likely is an elderly male patient with high Serum Calcium to have malignant cancer? P(C=malignant | Age>60, Gender= male, Serum Calcium = high) Lung Tumor © Jack Breese (Microsoft) & Daphne Koller (Stanford) 54
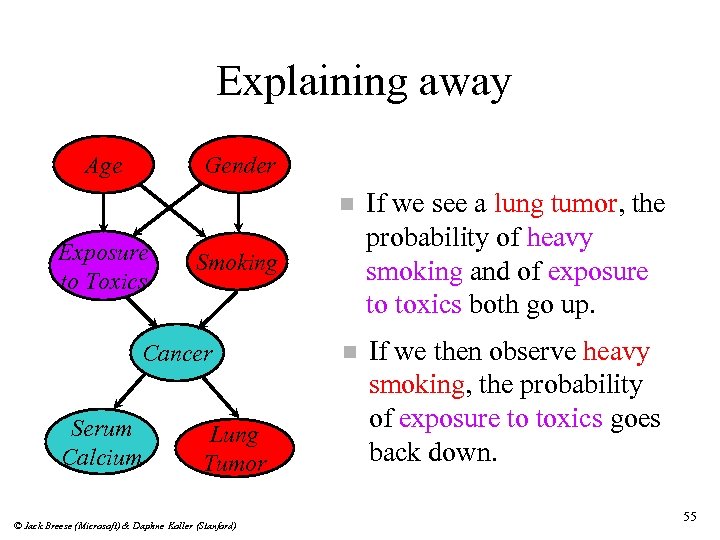
Explaining away Age Gender n Exposure to Toxics n If we then observe heavy smoking, the probability of exposure to toxics goes back down. Smoking Cancer Serum Calcium If we see a lung tumor, the probability of heavy smoking and of exposure to toxics both go up. Lung Tumor © Jack Breese (Microsoft) & Daphne Koller (Stanford) 55

Inference in Belief Networks n Find P(Q=q|E= e) u Q the query variable u E set of evidence variables P(q, e) P(q | e) = P(e) X 1, …, Xn are network variables except Q, E P(q, e) = S P(q, e, x 1, …, xn) x 1, …, xn © Jack Breese (Microsoft) & Daphne Koller (Stanford) 56
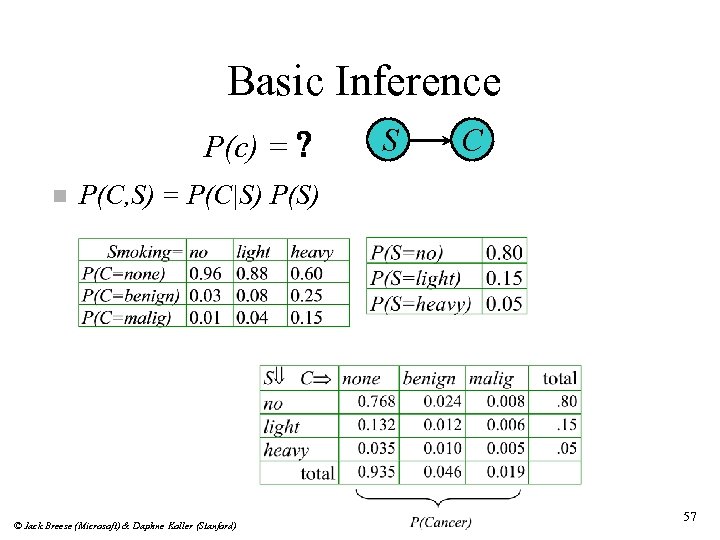
Basic Inference P(c) = ? n S C P(C, S) = P(C|S) P(S) © Jack Breese (Microsoft) & Daphne Koller (Stanford) 57
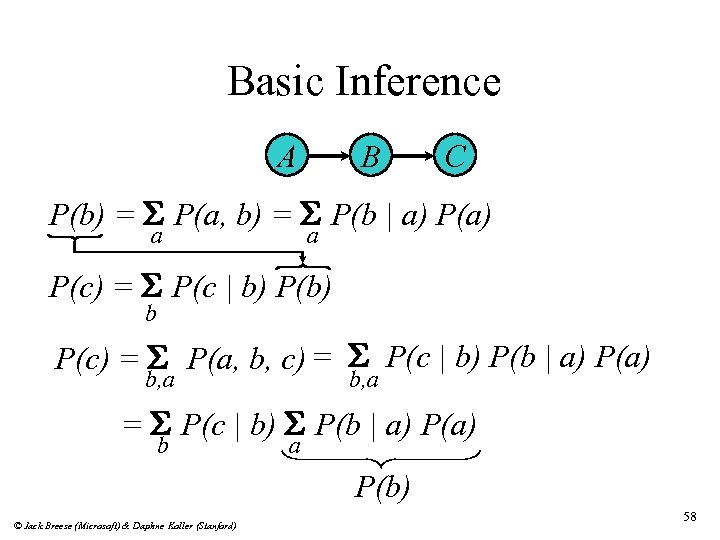
Basic Inference A B C P(b) = S P(a, b) = S P(b | a) P(a) a a P(c) = S P(c | b) P(b) b P(c) = S P(a, b, c) = S P(c | b) P(b | a) P(a) b, a = S P(c | b) S P(b | a) P(a) b a P(b) © Jack Breese (Microsoft) & Daphne Koller (Stanford) 58
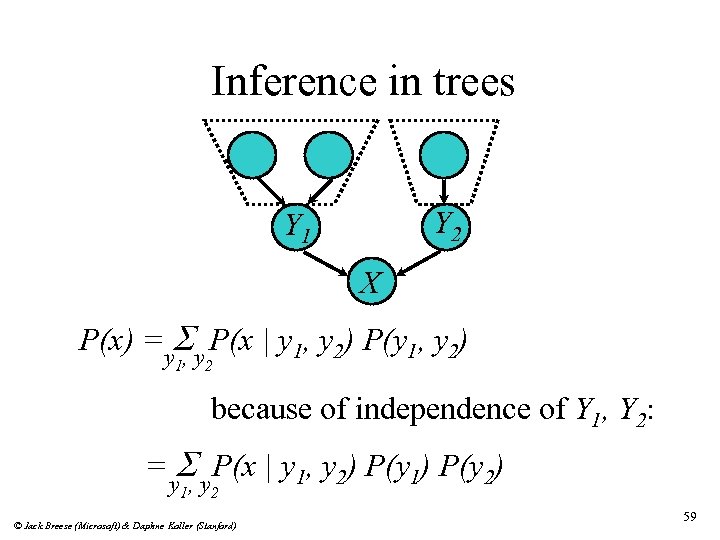
Inference in trees Y 2 Y 1 X P(x) =y. S y P(x | y 1, y 2) P(y 1, y 2) , 1 2 because of independence of Y 1, Y 2: = S P(x | y 1, y 2) P(y 1) P(y 2) y 1, y 2 © Jack Breese (Microsoft) & Daphne Koller (Stanford) 59
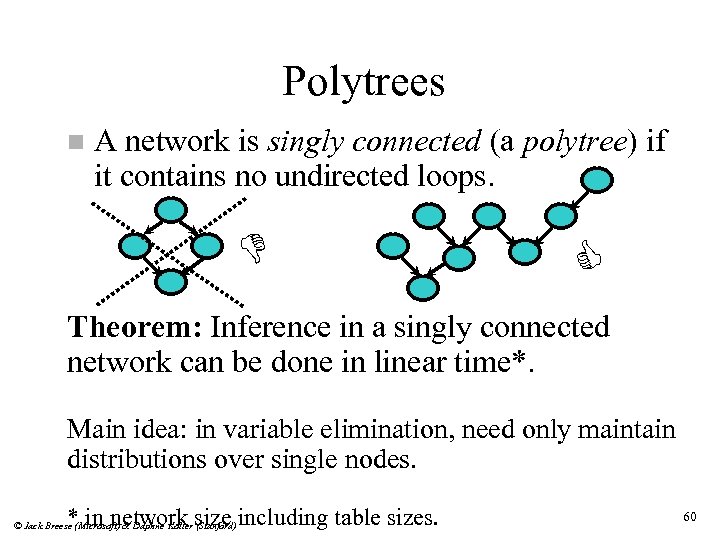
Polytrees n A network is singly connected (a polytree) if it contains no undirected loops. D C Theorem: Inference in a singly connected network can be done in linear time*. Main idea: in variable elimination, need only maintain distributions over single nodes. * in network size including table sizes. © Jack Breese (Microsoft) & Daphne Koller (Stanford) 60

The problem with loops P(c) 0. 5 c c Cloudy Rain P(r) 0. 99 0. 01 Sprinkler Grass-wet c c P(s) 0. 01 0. 99 deterministic or The grass is dry only if no rain and no sprinklers. P(g) = P(r, s) ~ 0 © Jack Breese (Microsoft) & Daphne Koller (Stanford) 61

The problem with loops contd. 0 P(g) = 0 P(g | r, s) P(r, s) + P(g | r, s) P(r, s) 0 1 = P(r, s) ~ 0 = P(r) P(s) ~ 0. 5 · 0. 5 = 0. 25 problem © Jack Breese (Microsoft) & Daphne Koller (Stanford) 62
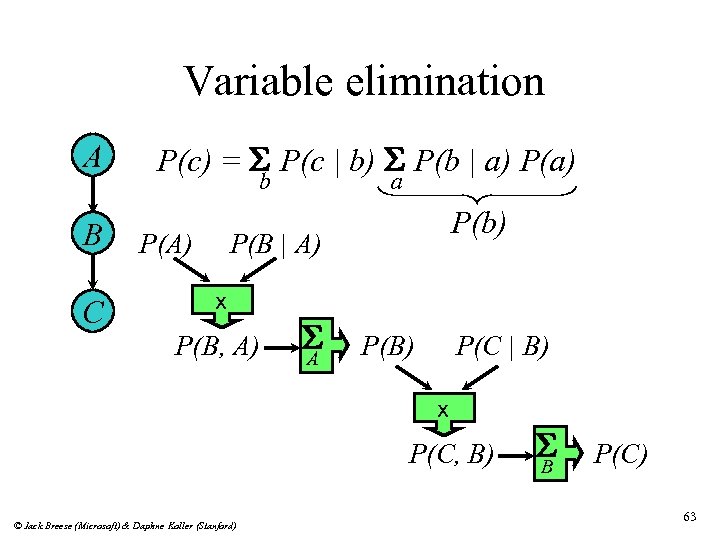
Variable elimination A B C P(c) = S P(c | b) S P(b | a) P(a) b P(A) a P(b) P(B | A) x P(B, A) S A P(B) P(C | B) x P(C, B) © Jack Breese (Microsoft) & Daphne Koller (Stanford) S B P(C) 63

Inference as variable elimination n A factor over X is a function from val(X) to numbers in [0, 1]: u. A CPT is a factor u A joint distribution is also a factor n BN inference: u factors are multiplied to give new ones u variables in factors summed out n A variable can be summed out as soon as all factors mentioning it have been multiplied. © Jack Breese (Microsoft) & Daphne Koller (Stanford) 64
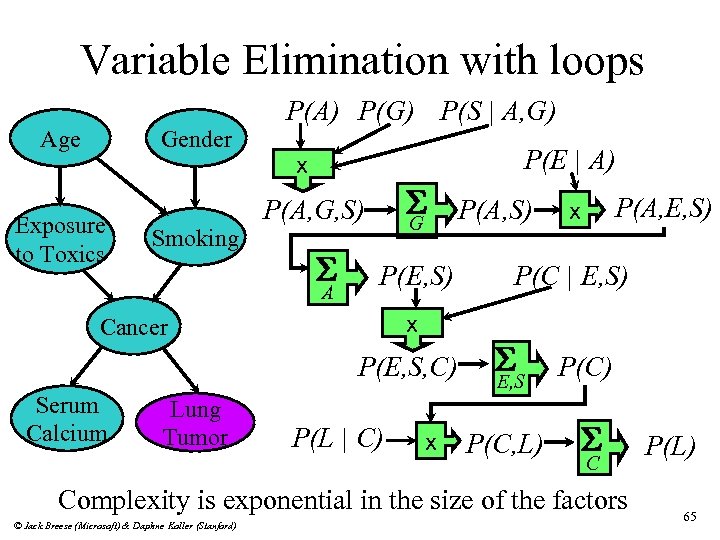
Variable Elimination with loops Age Gender Exposure to Toxics Smoking P(A) P(G) P(S | A, G) P(E | A) x S G P(A, G, S) S A P(E, S) x Cancer P(E, S, C) Serum Calcium Lung Tumor P(L | C) x P(A, S) P(A, E, S) x P(C | E, S) S E, S P(C) P(C, L) S C Complexity is exponential in the size of the factors © Jack Breese (Microsoft) & Daphne Koller (Stanford) P(L) 65
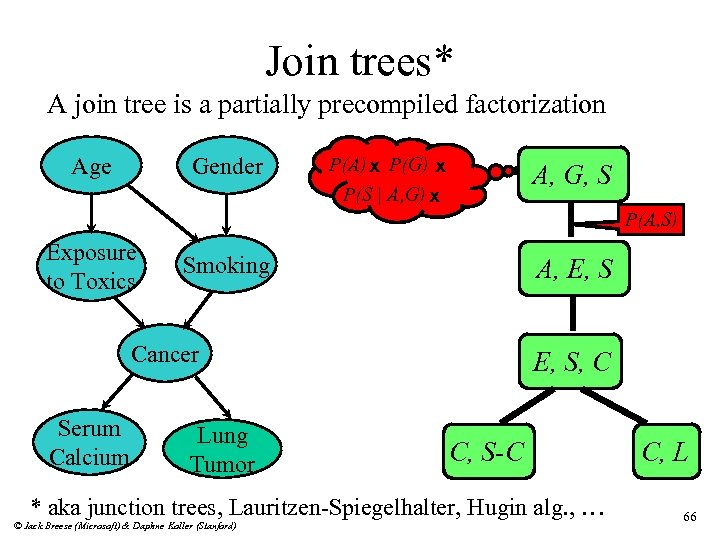
Join trees* A join tree is a partially precompiled factorization Age Gender P(A) x P(G) x P(S | A, G) x A, G, S P(A, S) Exposure to Toxics Smoking A, E, S Cancer Serum Calcium Lung Tumor E, S, C C, S-C * aka junction trees, Lauritzen-Spiegelhalter, Hugin alg. , … © Jack Breese (Microsoft) & Daphne Koller (Stanford) C, L 66
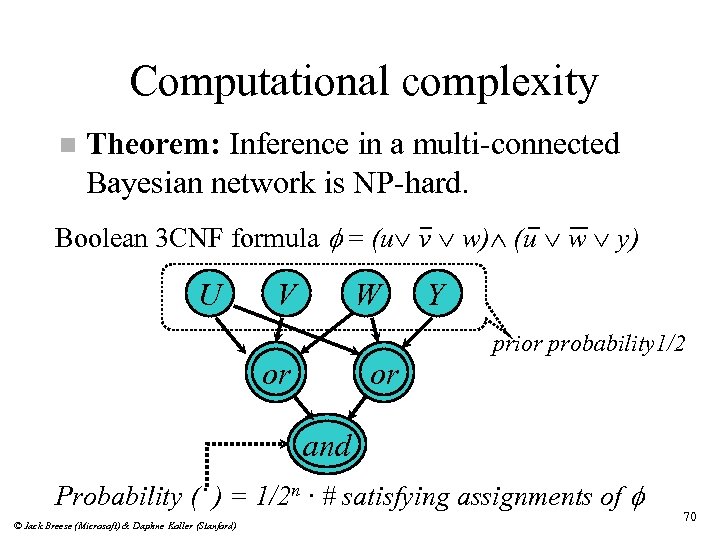
Computational complexity n Theorem: Inference in a multi-connected Bayesian network is NP-hard. Boolean 3 CNF formula f = (u v w) (u w y) U V W or or Y prior probability 1/2 and Probability ( ) = 1/2 n · # satisfying assignments of f © Jack Breese (Microsoft) & Daphne Koller (Stanford) 70
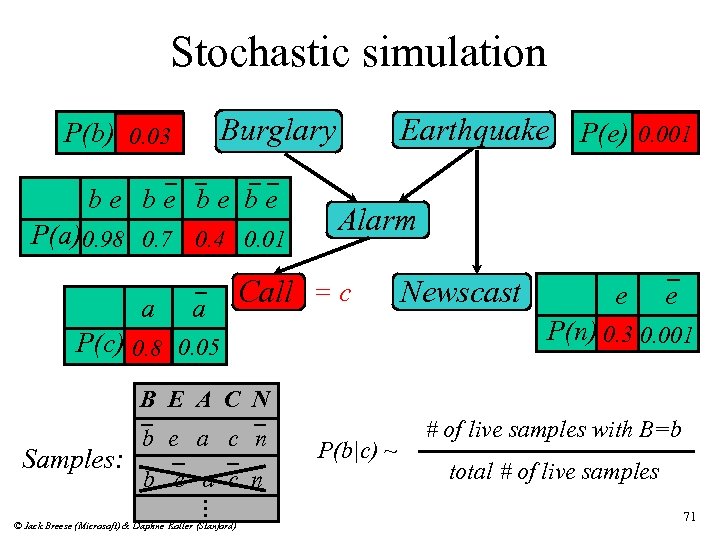
Stochastic simulation Burglary P(b) 0. 03 be be P(a) 0. 98 0. 7 0. 4 0. 01 a a Earthquake P(e) 0. 001 Alarm Call = c Newscast e e P(n) 0. 3 0. 001 P(c) 0. 8 0. 05 B E A C N Samples: b e a c n . . . © Jack Breese (Microsoft) & Daphne Koller (Stanford) P(b|c) ~ # of live samples with B=b total # of live samples 71
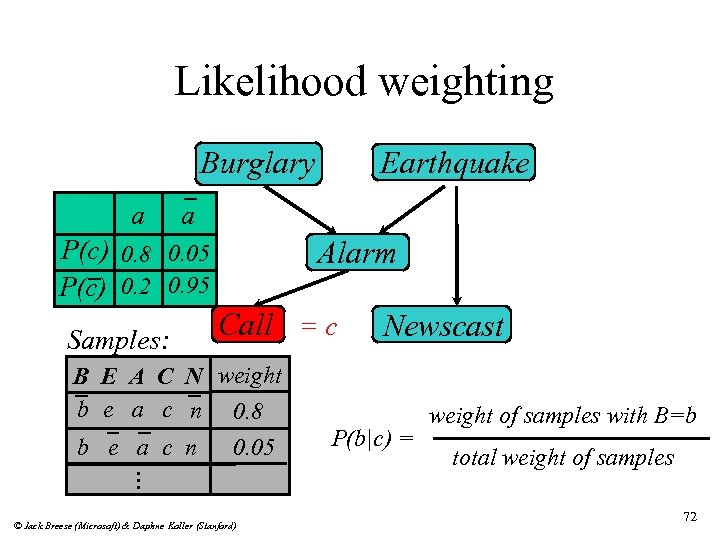
Likelihood weighting Burglary a a P(c) 0. 8 0. 05 P(c) 0. 2 0. 95 Samples: Earthquake Alarm Call = c B E A C N weight b e a c n 0. 8 b e a c n 0. 05 Newscast P(b|c) = weight of samples with B=b total weight of samples . . . © Jack Breese (Microsoft) & Daphne Koller (Stanford) 72

Markov Chain Monte Carlo 73

MCMC with Gibbs Sampling Fix the values of observed variables Set the values of all non-observed variables randomly Perform a random walk through the space of complete variable assignments. On each move: 1. Pick a variable X 2. Calculate Pr(X=true | all other variables) 3. Set X to true with that probability Repeat many times. Frequency with which any variable X is true is it’s posterior probability. Converges to true posterior when frequencies stop changing significantly • stable distribution, mixing 74

Markov Blanket Sampling How to calculate Pr(X=true | all other variables) ? Recall: a variable is independent of all others given it’s Markov Blanket • parents • children • other parents of children So problem becomes calculating Pr(X=true | MB(X)) • We solve this sub-problem exactly • Fortunately, it is easy to solve 75
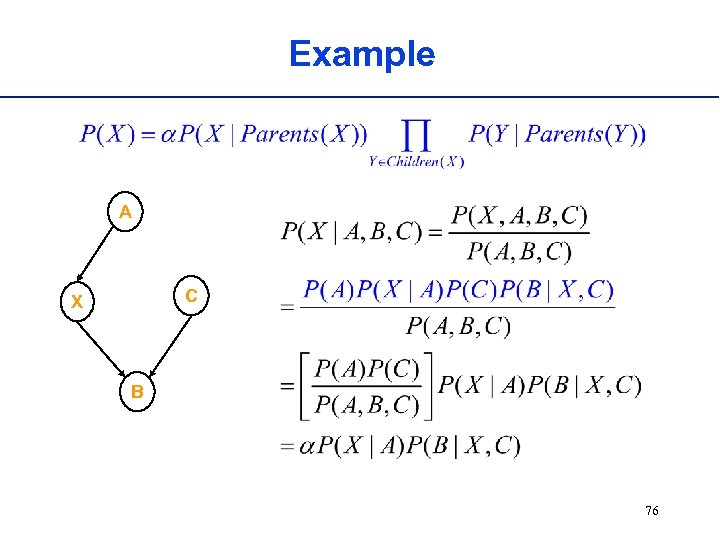
Example A C X B 76
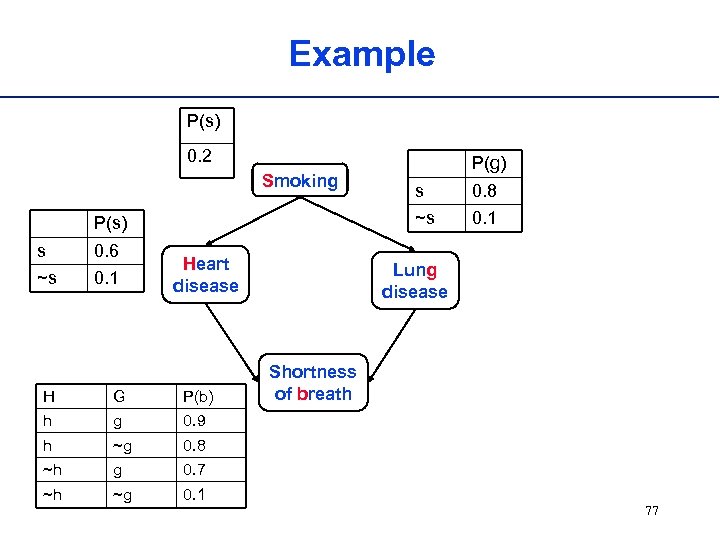
Example P(s) 0. 2 Smoking 0. 6 ~s 0. 1 Heart disease H G P(b) h g ~g 0. 1 Lung disease Shortness of breath 0. 7 ~h 0. 1 0. 8 ~h 0. 8 0. 9 h s ~s P(s) s P(g) 77
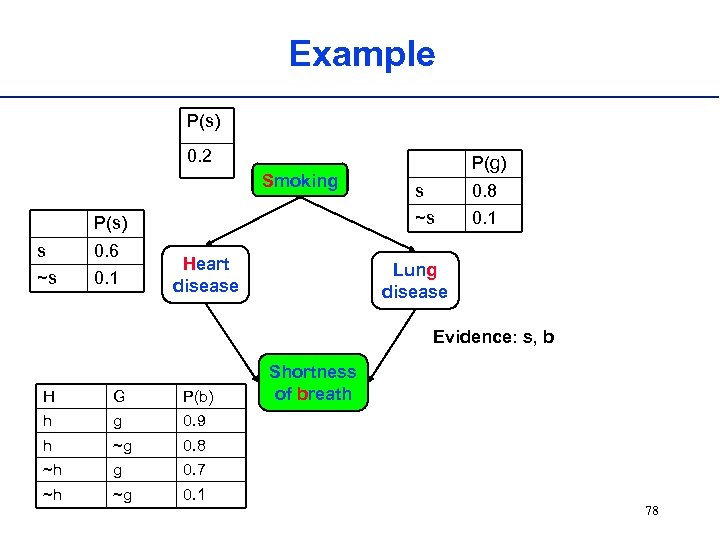
Example P(s) 0. 2 Smoking 0. 6 ~s 0. 1 Heart disease s 0. 8 ~s P(s) s P(g) 0. 1 Lung disease Evidence: s, b H G P(b) h g 0. 9 h ~g 0. 8 ~h g 0. 7 ~h ~g 0. 1 Shortness of breath 78
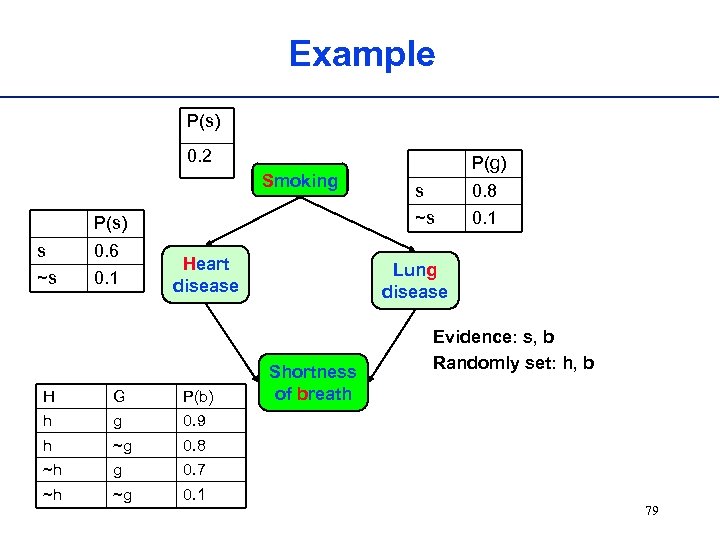
Example P(s) 0. 2 Smoking 0. 6 ~s 0. 1 Heart disease H G P(b) h g ~g 0. 1 Lung disease Shortness of breath Evidence: s, b Randomly set: h, b 0. 7 ~h 0. 1 0. 8 ~h 0. 8 0. 9 h s ~s P(s) s P(g) 79
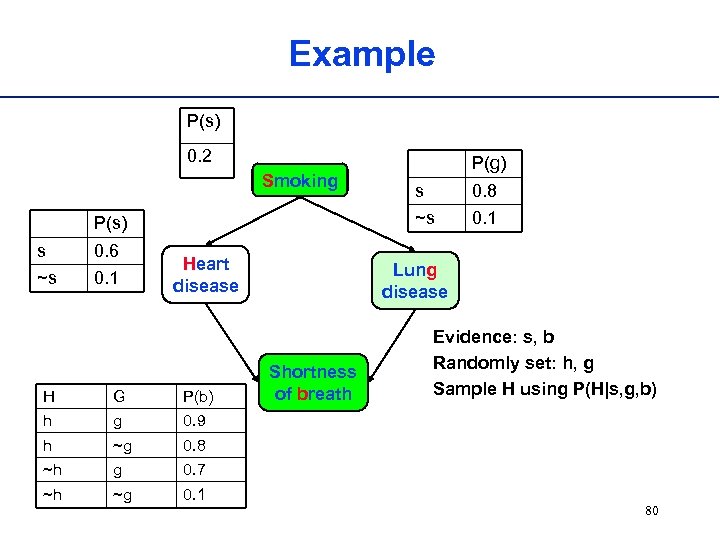
Example P(s) 0. 2 Smoking 0. 6 ~s 0. 1 Heart disease H G P(b) h g ~g 0. 1 Lung disease Shortness of breath Evidence: s, b Randomly set: h, g Sample H using P(H|s, g, b) 0. 7 ~h 0. 1 0. 8 ~h 0. 8 0. 9 h s ~s P(s) s P(g) 80
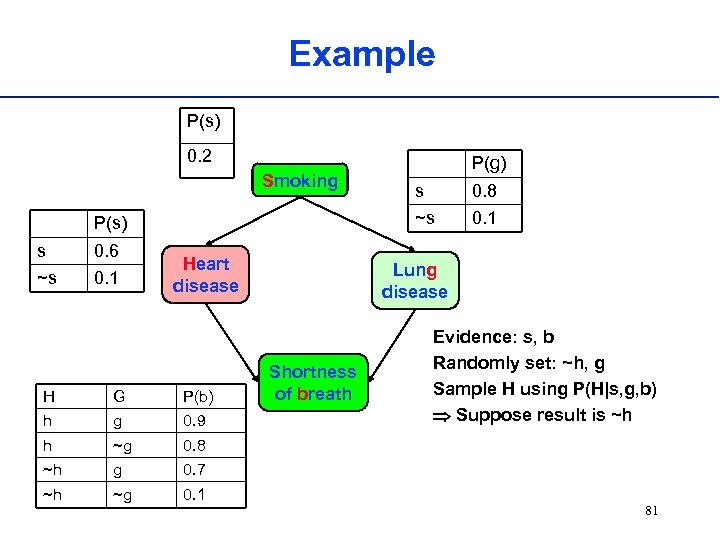
Example P(s) 0. 2 Smoking 0. 6 ~s 0. 1 Heart disease H G P(b) h g 0. 9 h ~g g ~g 0. 1 Lung disease Shortness of breath Evidence: s, b Randomly set: ~h, g Sample H using P(H|s, g, b) Suppose result is ~h 0. 7 ~h 0. 8 ~h s ~s P(s) s P(g) 81
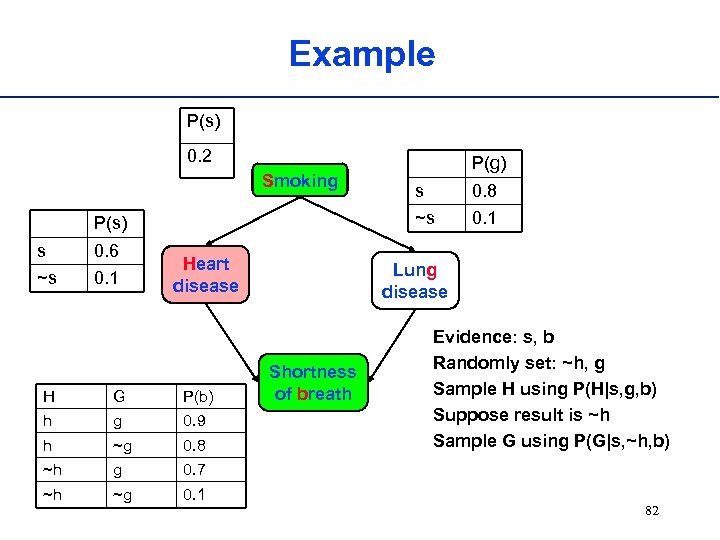
Example P(s) 0. 2 Smoking 0. 6 ~s 0. 1 Heart disease H G P(b) h g 0. 9 h ~g 0. 8 ~h g ~g 0. 1 0. 8 0. 1 Lung disease Shortness of breath Evidence: s, b Randomly set: ~h, g Sample H using P(H|s, g, b) Suppose result is ~h Sample G using P(G|s, ~h, b) 0. 7 ~h s ~s P(s) s P(g) 82
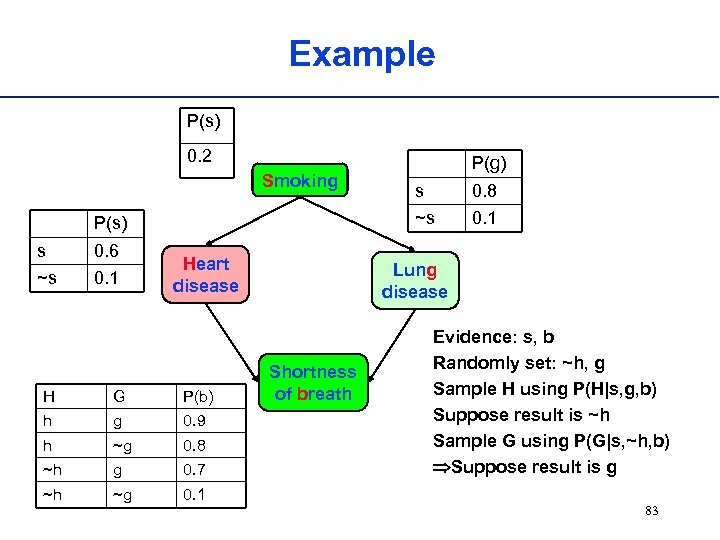
Example P(s) 0. 2 Smoking 0. 6 ~s 0. 1 Heart disease H G P(b) h g 0. 9 h ~g 0. 8 ~h g 0. 7 ~h ~g 0. 1 s 0. 8 ~s P(s) s P(g) 0. 1 Lung disease Shortness of breath Evidence: s, b Randomly set: ~h, g Sample H using P(H|s, g, b) Suppose result is ~h Sample G using P(G|s, ~h, b) Suppose result is g 83
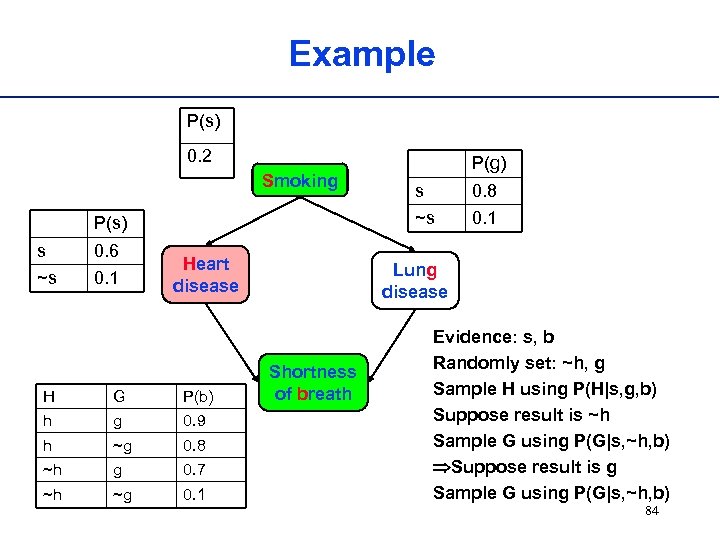
Example P(s) 0. 2 Smoking 0. 6 ~s 0. 1 Heart disease H G P(b) h g 0. 9 h ~g 0. 8 ~h g 0. 7 ~h ~g 0. 1 s 0. 8 ~s P(s) s P(g) 0. 1 Lung disease Shortness of breath Evidence: s, b Randomly set: ~h, g Sample H using P(H|s, g, b) Suppose result is ~h Sample G using P(G|s, ~h, b) Suppose result is g Sample G using P(G|s, ~h, b) 84
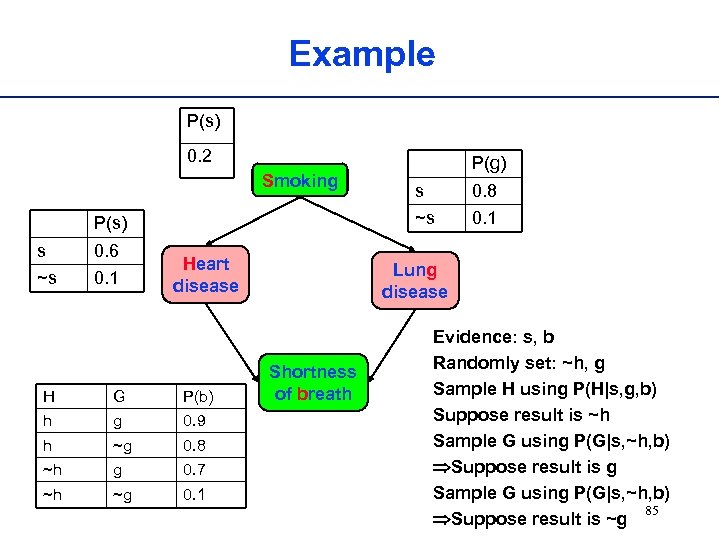
Example P(s) 0. 2 Smoking 0. 6 ~s 0. 1 Heart disease H G P(b) h g 0. 9 h ~g 0. 8 ~h g 0. 7 ~h ~g 0. 1 s 0. 8 ~s P(s) s P(g) 0. 1 Lung disease Shortness of breath Evidence: s, b Randomly set: ~h, g Sample H using P(H|s, g, b) Suppose result is ~h Sample G using P(G|s, ~h, b) Suppose result is g Sample G using P(G|s, ~h, b) 85 Suppose result is ~g

Gibbs MCMC Summary P(X|E) = number of samples with X=x total number of samples Advantages: • No samples are discarded • No problem with samples of low weight • Can be implemented very efficiently – 10 K samples @ second Disadvantages: • Can get stuck if relationship between two variables is deterministic • Many variations have been devised to make MCMC more robust 86

Other approaches n Search based techniques u search for high-probability instantiations u use instantiations to approximate probabilities n Structural approximation u simplify network n eliminate edges, nodes n abstract node values n simplify CPTs u do inference in simplified network © Jack Breese (Microsoft) & Daphne Koller (Stanford) 87

Course Contents Concepts in Probability n Bayesian Networks n Inference n Decision making » Learning networks from data n Reasoning over time n Applications n © Jack Breese (Microsoft) & Daphne Koller (Stanford) 107

Learning networks from data The learning task n Parameter learning n u Fully observable u Partially observable Structure learning n Hidden variables n © Jack Breese (Microsoft) & Daphne Koller (Stanford) 108
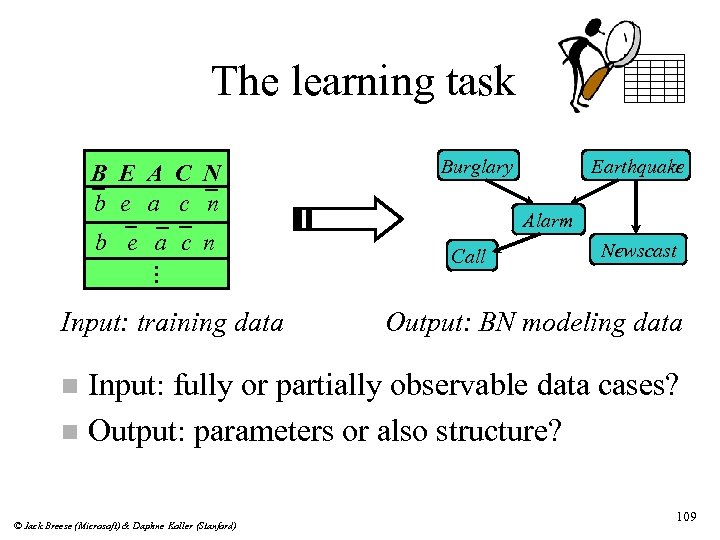
The learning task B E A C N b e a c n . . . Input: training data Burglary Earthquake Alarm Call Newscast Output: BN modeling data Input: fully or partially observable data cases? n Output: parameters or also structure? n © Jack Breese (Microsoft) & Daphne Koller (Stanford) 109

Parameter learning: one variable n Unfamiliar coin: u Let n If q known (given), then u P(X n q = bias of coin (long-run fraction of heads) = heads | q ) = q Different coin tosses independent given q P(X 1, …, Xn | q ) = q h (1 -q)t h heads, t tails © Jack Breese (Microsoft) & Daphne Koller (Stanford) 110

Maximum likelihood n Input: a set of previous coin tosses u X 1, …, Xn = {H, T, H, H, H, T, T, H, . . . , H} h heads, t tails n Goal: estimate q n The likelihood P(X 1, …, Xn | q ) = q h (1 -q )t n The maximum likelihood solution is: q* = h h+t © Jack Breese (Microsoft) & Daphne Koller (Stanford) 111

General parameter learning n A multi-variable BN is composed of several independent parameters (“coins”). A n B Three parameters: q. A, q. B|a Can use same techniques as one-variable case to learn each one separately Max likelihood estimate of q. B|a would be: q* B|a = © Jack Breese (Microsoft) & Daphne Koller (Stanford) #data cases with b, a #data cases with a 115
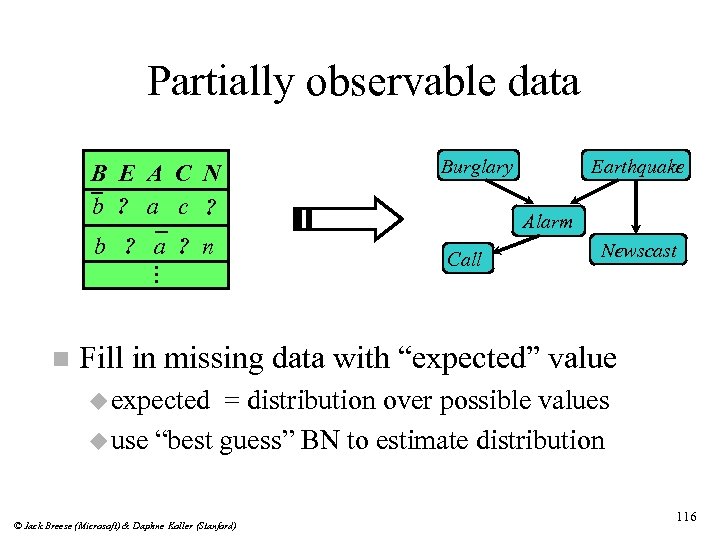
Partially observable data B E A C N b ? a c ? b ? a ? n . . . n Burglary Earthquake Alarm Call Newscast Fill in missing data with “expected” value u expected = distribution over possible values u use “best guess” BN to estimate distribution © Jack Breese (Microsoft) & Daphne Koller (Stanford) 116

Intuition n In fully observable case: #data cases with n, e n|e = #data cases with e = q* I(e | dj) = n Sj I(n, e | dj) S j I(e | dj) 1 if E=e in data case dj 0 otherwise In partially observable case I is unknown. Best estimate for I is: Problem: q* unknown. © Jack Breese (Microsoft) & Daphne Koller (Stanford) 117

Expectation Maximization (EM) Repeat : n Expectation (E) step u Use n Maximization (M) step u Use n current parameters q to estimate filled in data to do max likelihood estimation Set: until convergence. © Jack Breese (Microsoft) & Daphne Koller (Stanford) 118

Structure learning Goal: find “good” BN structure (relative to data) Solution: do heuristic search over space of network structures. © Jack Breese (Microsoft) & Daphne Koller (Stanford) 119
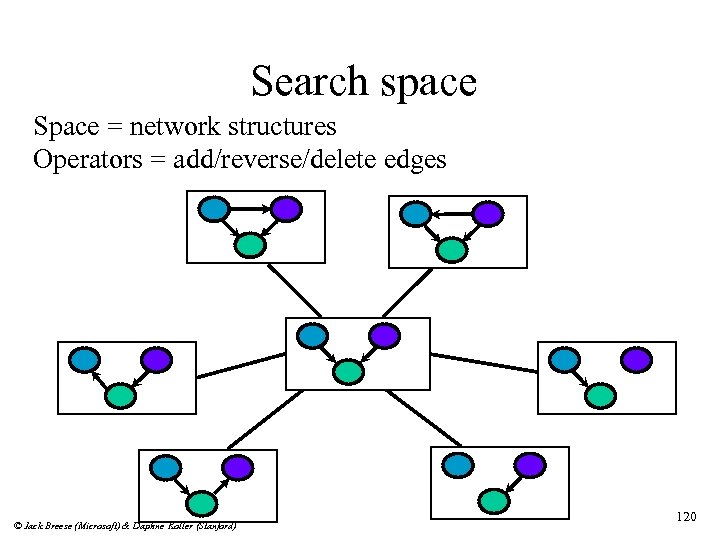
Search space Space = network structures Operators = add/reverse/delete edges © Jack Breese (Microsoft) & Daphne Koller (Stanford) 120
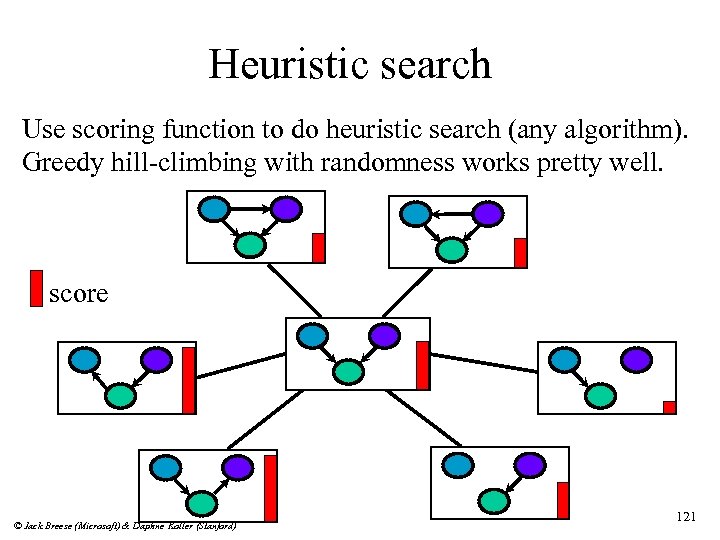
Heuristic search Use scoring function to do heuristic search (any algorithm). Greedy hill-climbing with randomness works pretty well. score © Jack Breese (Microsoft) & Daphne Koller (Stanford) 121

Scoring Fill in parameters using previous techniques & score completed networks. n One possibility for score: n likelihood function: Score(B) = P(data | B) D Example: X, Y independent coin tosses typical data = (27 h-h, 22 h-t, 25 t-h, 26 t-t) Maximum likelihood network structure: X Y Max. likelihood network typically fully connected This is not surprising: maximum likelihood always overfits… © Jack Breese (Microsoft) & Daphne Koller (Stanford) 122

Better scoring functions n MDL formulation: balance fit to data and model complexity (# of parameters) Score(B) = P(data | B) - model complexity n Full Bayesian formulation u prior on network structures & parameters u more parameters higher dimensional space u get balance effect as a byproduct* * with Dirichlet parameter prior, MDL is an approximation to full Bayesian score. © Jack Breese (Microsoft) & Daphne Koller (Stanford) 123

Course Contents Concepts in Probability n Bayesian Networks n Inference n Decision making n Learning networks from data n Reasoning over time » Applications n © Jack Breese (Microsoft) & Daphne Koller (Stanford) 146

Applications n Medical expert systems u Pathfinder u Parenting n MSN Fault diagnosis u Ricoh FIXIT u Decision-theoretic troubleshooting Vista n Collaborative filtering n © Jack Breese (Microsoft) & Daphne Koller (Stanford) 147

Why use Bayesian Networks? n Explicit management of uncertainty/tradeoffs n Modularity implies maintainability n Better, flexible, and robust recommendation strategies © Jack Breese (Microsoft) & Daphne Koller (Stanford) 148

Pathfinder is one of the first BN systems. n It performs diagnosis of lymph-node diseases. n It deals with over 60 diseases and 100 findings. n Commercialized by Intellipath and Chapman Hall publishing and applied to about 20 tissue types. n © Jack Breese (Microsoft) & Daphne Koller (Stanford) 149

On Parenting: Selecting problem n n n Diagnostic indexing for Home Health site on Microsoft Network Enter symptoms for pediatric complaints Recommends multimedia content © Jack Breese (Microsoft) & Daphne Koller (Stanford) 152
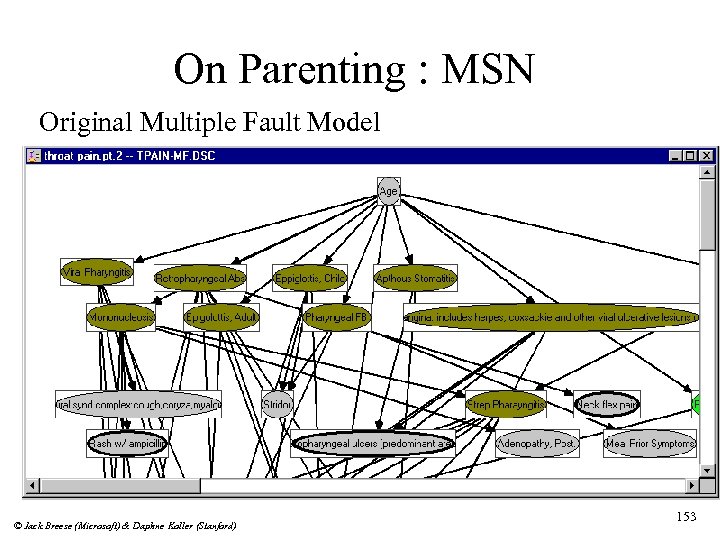
On Parenting : MSN Original Multiple Fault Model © Jack Breese (Microsoft) & Daphne Koller (Stanford) 153
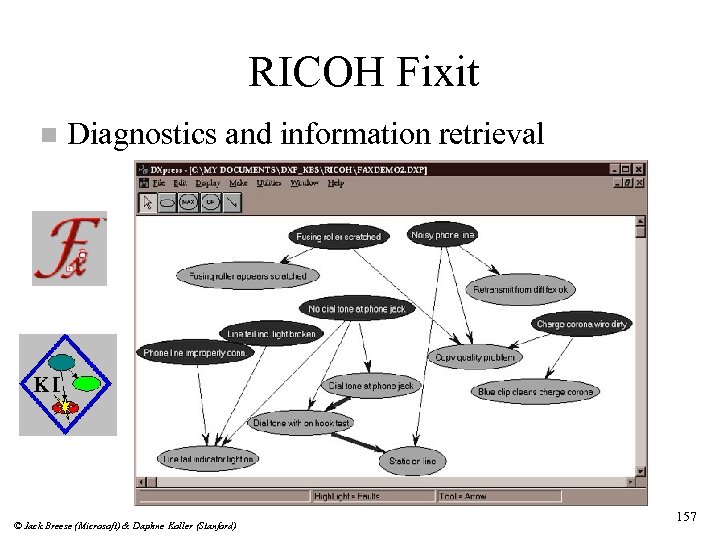
RICOH Fixit n Diagnostics and information retrieval © Jack Breese (Microsoft) & Daphne Koller (Stanford) 157

What is Collaborative Filtering? A way to find cool websites, news stories, music artists etc n Uses data on the preferences of many users, not descriptions of the content. n Firefly, Net Perceptions (Group. Lens), and others offer this technology. n © Jack Breese (Microsoft) & Daphne Koller (Stanford) 170

Bayesian Clustering for Collaborative Filtering Probabilistic summary of the data n Reduces the number of parameters to represent a set of preferences n Provides insight into usage patterns. n Inference: n P(Like title i | Like title j, Like title k) © Jack Breese (Microsoft) & Daphne Koller (Stanford) 171
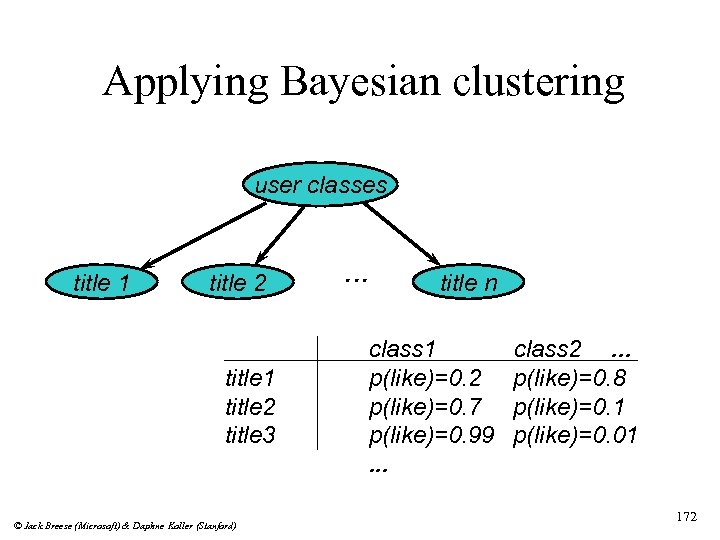
Applying Bayesian clustering user classes title 1 title 2 title 3 © Jack Breese (Microsoft) & Daphne Koller (Stanford) . . . title n class 1 p(like)=0. 2 p(like)=0. 7 p(like)=0. 99. . . class 2. . . p(like)=0. 8 p(like)=0. 1 p(like)=0. 01 172

MSNBC Story clusters Readers of commerce and technology stories (36%): n n n E-mail delivery isn't exactly guaranteed Should you buy a DVD player? Price low, demand high for Nintendo Sports Readers (19%): n n n Umps refusing to work is the right thing Cowboys are reborn in win over eagles Did Orioles spend money wisely? © Jack Breese (Microsoft) & Daphne Koller (Stanford) Readers of top promoted stories (29%): n n n 757 Crashes At Sea Israel, Palestinians Agree To Direct Talks Fuhrman Pleads Innocent To Perjury Readers of “Softer” News (12%): n n n The truth about what things cost Fuhrman Pleads Innocent To Perjury Real Astrology 173

Top 5 shows by user class Class 1 • Power rangers • Animaniacs • X-men • Tazmania • Spider man Class 2 • Young and restless • Bold and the beautiful • As the world turns • Price is right • CBS eve news Class 4 • 60 minutes • NBC nightly news • CBS eve news • Murder she wrote • Matlock © Jack Breese (Microsoft) & Daphne Koller (Stanford) Class 3 • Tonight show • Conan O’Brien • NBC nightly news • Later with Kinnear • Seinfeld Class 5 • Seinfeld • Friends • Mad about you • ER • Frasier 174
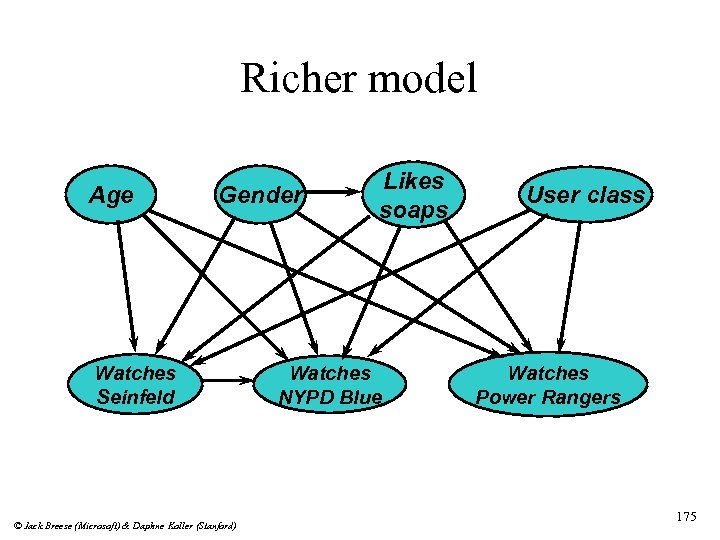
Richer model Age Gender Watches Seinfeld © Jack Breese (Microsoft) & Daphne Koller (Stanford) Likes soaps Watches NYPD Blue User class Watches Power Rangers 175

What’s old? Decision theory & probability theory provide: principled models of belief and preference; n techniques for: n u integrating evidence (conditioning); u optimal decision making (max. expected utility); u targeted information gathering (value of info. ); u parameter estimation from data. © Jack Breese (Microsoft) & Daphne Koller (Stanford) 176
What’s new? Bayesian networks exploit domain structure to allow compact representations of complex models. Knowledge Acquisition Learning Structured Representation © Jack Breese (Microsoft) & Daphne Koller (Stanford) Inference 177

What’s in our future? n Better models for: Structured Representation u preferences & utilities; u not-so-precise numerical probabilities. Inferring causality from data. n More expressive representation languages: n u structured domains with multiple objects; u levels of abstraction; u reasoning about time; u hybrid (continuous/discrete) models. © Jack Breese (Microsoft) & Daphne Koller (Stanford) 179
4b542d582763b043fc2603bb643e9ce7.ppt