7ce468d83df4e6a7452f11db6efa5a53.ppt
- Количество слайдов: 35

TUTORIAL 6 Chapter 10 Hypothesis Testing Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. Chap 8 -1

What is a Hypothesis? n A hypothesis is a claim (assumption) about a population parameter: n population mean Example: The mean monthly cell phone bill of this city is = $42 n population proportion Example: The proportion of adults in this city with cell phones is p =. 68 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 2

The Null Hypothesis, H 0 n States the assumption (numerical) to be tested Example: The average number of TV sets in U. S. Homes is at least three ( ) n Is always about a population parameter, not about a sample statistic Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 3

The Null Hypothesis, H 0 n n (continued) Begin with the assumption that the null hypothesis is true n Similar to the notion of innocent until proven guilty Refers to the status quo Always contains “=” , “≤” or “ ” sign May or may not be rejected Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 4

The Alternative Hypothesis, HA n Is the opposite of the null hypothesis n n n e. g. : The average number of TV sets in U. S. homes is less than 3 ( HA: < 3 ) Challenges the status quo Never contains the “=” , “≤” or “ ” sign May or may not be accepted Is generally the hypothesis that is believed (or needs to be supported) by the researcher Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 5
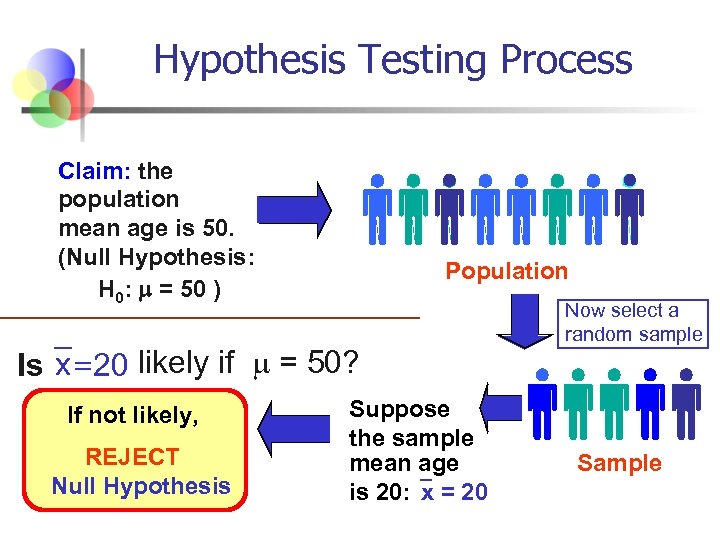
Hypothesis Testing Process Claim: the population mean age is 50. (Null Hypothesis: H 0: = 50 ) Population Is x = 20 likely if = 50? If not likely, REJECT Null Hypothesis Suppose the sample mean age is 20: x = 20 Now select a random sample Sample
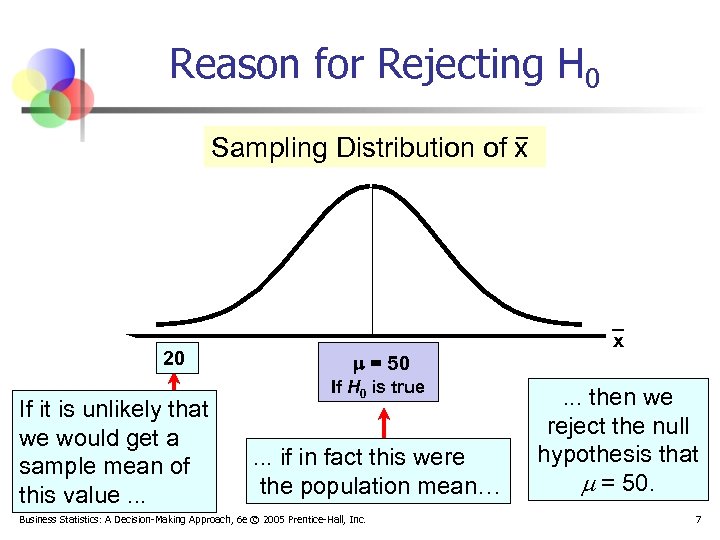
Reason for Rejecting H 0 Sampling Distribution of x 20 If it is unlikely that we would get a sample mean of this value. . . = 50 If H 0 is true . . . if in fact this were the population mean… Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. x . . . then we reject the null hypothesis that = 50. 7

Level of Significance, n Defines unlikely values of sample statistic if null hypothesis is true n n Defines rejection region of the sampling distribution Is designated by , (level of significance) n Typical values are. 01, . 05, or. 10 n Is selected by the researcher at the beginning n Provides the critical value(s) of the test Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 8

Errors in Making Decisions n Type I Error n Reject a true null hypothesis n Considered a serious type of error The probability of Type I Error is n Called level of significance of the test n Set by researcher in advance Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 9

Errors in Making Decisions (continued) n Type II Error n Fail to reject a false null hypothesis The probability of Type II Error is β Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 10

Outcomes and Probabilities Possible Hypothesis Test Outcomes State of Nature Decision Key: Outcome (Probability) H 0 True Do Not Reject H 0 No error (1 - ) Type II Error (β) Reject H 0 Type I Error ( ) No Error (1 -β) Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. H 0 False 11

Lower Tail Tests n H 0: μ ≥ 3 The cutoff value, H A: μ < 3 -zα or xα , is called a critical value Reject H 0 -zα xα Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. Do not reject H 0 0 μ 12

Upper Tail Tests n The cutoff value, zα or xα , is called a critical value H 0: μ ≤ 3 H A: μ > 3 Do not reject H 0 0 μ Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. zα Reject H 0 xα 13
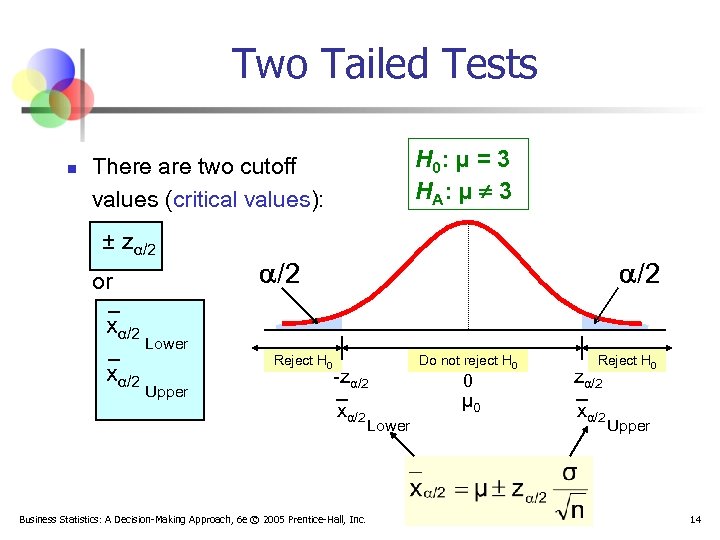
Two Tailed Tests n H 0: μ = 3 H A: μ ¹ 3 There are two cutoff values (critical values): ± zα/2 or xα/2 /2 Lower Reject H 0 Upper -zα/2 xα/2 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. Lower Do not reject H 0 0 μ 0 Reject H 0 zα/2 xα/2 Upper 14

Review: Steps in Hypothesis Testing n n 1. Specify the population value of interest 2. Formulate the appropriate null and alternative hypotheses n 3. Specify the desired level of significance n 4. Determine the rejection region n n 5. Obtain sample evidence and compute the test statistic 6. Reach a decision and interpret the result Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 15

Hypothesis Testing Example Test the claim that the true mean # of TV sets in US homes is at least 3. (Assume σ = 0. 8) n n n 1. Specify the population value of interest n The mean number of TVs in US homes 2. Formulate the appropriate null and alternative hypotheses n H 0: μ 3 HA: μ < 3 (This is a lower tail test) 3. Specify the desired level of significance n Suppose that =. 05 is chosen for this test Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 16

Hypothesis Testing Example (continued) n 4. Determine the rejection region =. 05 Reject H 0 Do not reject H 0 -zα= -1. 645 0 This is a one-tailed test with =. 05. Since σ is known, the cutoff value is a z value: Reject H 0 if z < z = -1. 645 ; otherwise do not reject H 0 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 17

Hypothesis Testing Example n 5. Obtain sample evidence and compute the test statistic Suppose a sample is taken with the following results: n = 100, x = 2. 84 ( = 0. 8 is assumed known) n Then the test statistic is: Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 18
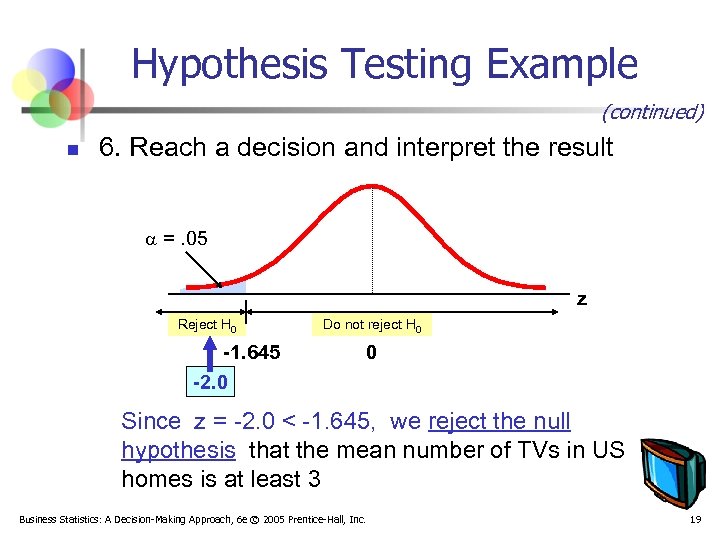
Hypothesis Testing Example (continued) n 6. Reach a decision and interpret the result =. 05 z Reject H 0 -1. 645 -2. 0 Do not reject H 0 0 Since z = -2. 0 < -1. 645, we reject the null hypothesis that the mean number of TVs in US homes is at least 3 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 19
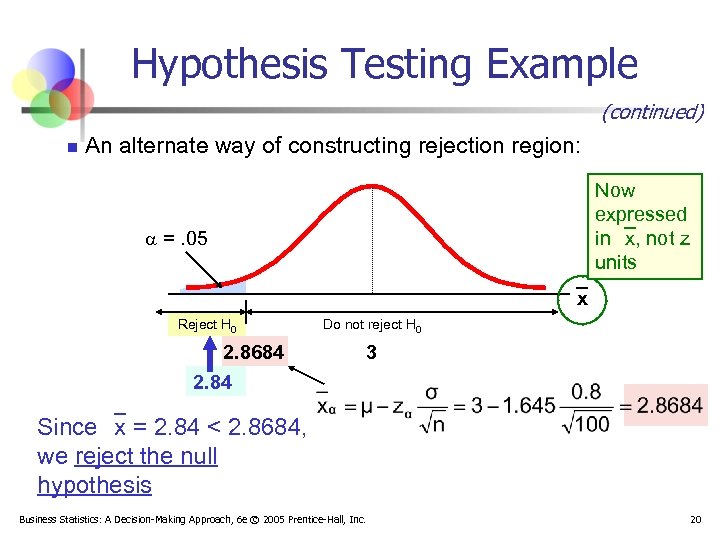
Hypothesis Testing Example (continued) n An alternate way of constructing rejection region: Now expressed in x, not z units =. 05 x Reject H 0 2. 8684 2. 84 Do not reject H 0 3 Since x = 2. 84 < 2. 8684, we reject the null hypothesis Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 20

p-Value Approach to Testing n Convert Sample Statistic (e. g. x ) to Test Statistic ( Z or t statistic ) n Obtain the p-value from a table or computer n Compare the p-value with n If p-value < , reject H 0 n If p-value , do not reject H 0 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 21

p-Value Approach to Testing (continued) n p-value: Probability of obtaining a test statistic more extreme ( ≤ or ) than the observed sample value given H 0 is true n n Also called observed level of significance Smallest value of for which H 0 can be rejected Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 22
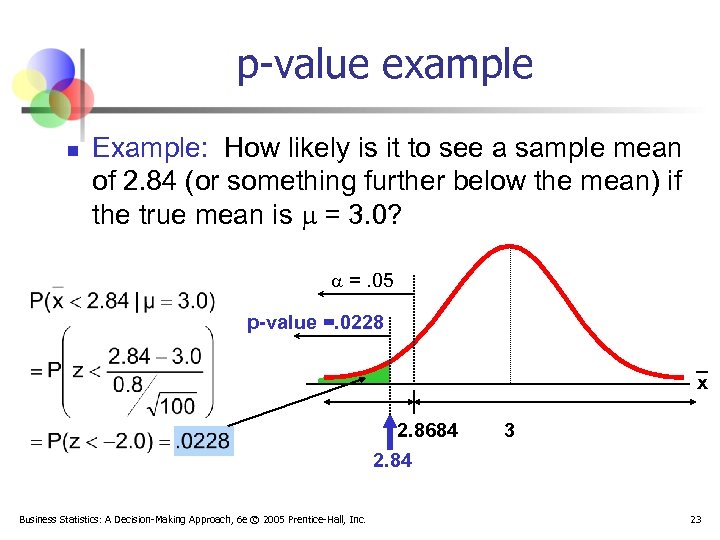
p-value example n Example: How likely is it to see a sample mean of 2. 84 (or something further below the mean) if the true mean is = 3. 0? =. 05 p-value =. 0228 x 2. 8684 2. 84 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 3 23

p-value example (continued) n Compare the p-value with n If p-value < , reject H 0 n If p-value , do not reject H 0 =. 05 Here: p-value =. 0228 =. 05 Since. 0228 <. 05, we reject the null hypothesis p-value =. 0228 2. 8684 3 2. 84 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 24

Example: Upper Tail z Test for Mean ( Known) A phone industry manager thinks that customer monthly cell phone bill have increased, and now average over $52 per month. The company wishes to test this claim. (Assume = 10 is known) Form hypothesis test: H 0: μ ≤ 52 the average is not over $52 per month HA: μ > 52 the average is greater than $52 per month (i. e. , sufficient evidence exists to support the manager’s claim) Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 25

Example: Find Rejection Region (continued) n Suppose that =. 10 is chosen for this test Find the rejection region: Reject H 0 =. 10 Do not reject H 0 0 zα=1. 28 Reject H 0 if z > 1. 28 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 26

Review: Finding Critical Value - One Tail What is z given = 0. 10? . 90 . 10 =. 10. 50. 40 z Standard Normal Distribution Table (Portion) 0 1. 28 Z . 07 . 08 . 09 1. 1. 3790. 3810. 3830 1. 2. 3980. 3997. 4015 1. 3. 4147. 4162. 4177 Critical Value = 1. 28 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 27

Example: Test Statistic (continued) Obtain sample evidence and compute the test statistic Suppose a sample is taken with the following results: n = 64, x = 53. 1 ( =10 was assumed known) n Then the test statistic is: Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 28

Example: Decision (continued) Reach a decision and interpret the result: Reject H 0 =. 10 Do not reject H 0 1. 28 0 z =. 88 Reject H 0 Do not reject H 0 since z = 0. 88 ≤ 1. 28 i. e. : there is not sufficient evidence that the mean bill is over $52 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 29

p -Value Solution (continued) Calculate the p-value and compare to p-value =. 1894 Reject H 0 =. 10 0 Do not reject H 0 1. 28 z =. 88 Reject H 0 Do not reject H 0 since p-value =. 1894 > =. 10 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 30

Example: Two-Tail Test ( Unknown) The average cost of a hotel room in New York is said to be $168 per night. A random sample of 25 hotels resulted in x = $172. 50 and s = $15. 40. Test at the = 0. 05 level. H 0: μ = 168 HA: μ ¹ 168 (Assume the population distribution is normal) Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 31

Example Solution: Two-Tail Test H 0: μ = 168 HA: μ ¹ 168 § = 0. 05 § n = 25 /2=. 025 Reject H 0 -tα/2 -2. 0639 § is unknown, so use a t statistic /2=. 025 Do not reject H 0 0 1. 46 Reject H 0 tα/2 2. 0639 § Critical Value: t 24 = ± 2. 0639 Do not reject H 0: not sufficient evidence that true mean cost is different than $168 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 32

Example: z Test for Proportion A marketing company claims that it receives 8% responses from its mailing. To test this claim, a random sample of 500 were surveyed with 25 responses. Test at the =. 05 significance level. Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. Check: n p = (500)(. 08) = 40 n(1 -p) = (500)(. 92) = 460 33

Z Test for Proportion: Solution Test Statistic: H 0: p =. 08 HA: p ¹. 08 =. 05 n = 500, p =. 05 Decision: Critical Values: ± 1. 96 Reject . 025 -1. 96 0 1. 96 z -2. 47 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. Reject H 0 at =. 05 Conclusion: There is sufficient evidence to reject the company’s claim of 8% response rate. 34

p -Value Solution (continued) Calculate the p-value and compare to (For a two sided test the p-value is always two sided) Do not reject H 0 Reject H 0 /2 =. 025 Reject H 0 p-value =. 0136: /2 =. 025 . 0068 -1. 96 z = -2. 47 0 1. 96 z = 2. 47 Reject H 0 since p-value =. 0136 < =. 05 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 35
7ce468d83df4e6a7452f11db6efa5a53.ppt