тэс4-432 - копия.ppt
- Количество слайдов: 24
 ТУСУР Теория электрической связи Часть 4 Профессор кафедры радиотехнических систем, д. т. н. Юрий Павлович Акулиничев
ТУСУР Теория электрической связи Часть 4 Профессор кафедры радиотехнических систем, д. т. н. Юрий Павлович Акулиничев
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 2 Теория информации Собственная информация и избыточность (цифровые сигналы) Х - это m-ичный символ, а х1, x 2, …, xm - его возможные значения xj p(xj) x 1 p(x 1) x 2 p(x 2) … … xm p(xm) I(xj)= - loga p(xj) – собственная информация символа хj. Пример – импульс с двукратной ФМ: xj = j 0 90 180 270 p(xj) 0, 10 0, 60 0, 18 0, 12 I(xj) 3, 32 0, 74 2, 47 3, 06 1 нат. ед. = log 2 e бит 1, 443 бит, 1 дес. ед. = log 210 бит 3, 32 бит.
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 2 Теория информации Собственная информация и избыточность (цифровые сигналы) Х - это m-ичный символ, а х1, x 2, …, xm - его возможные значения xj p(xj) x 1 p(x 1) x 2 p(x 2) … … xm p(xm) I(xj)= - loga p(xj) – собственная информация символа хj. Пример – импульс с двукратной ФМ: xj = j 0 90 180 270 p(xj) 0, 10 0, 60 0, 18 0, 12 I(xj) 3, 32 0, 74 2, 47 3, 06 1 нат. ед. = log 2 e бит 1, 443 бит, 1 дес. ед. = log 210 бит 3, 32 бит.
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Клод Элвуд Шеннон Claude Elwood Shannon Гениальный американский математик и электротехник, один из создателей математической теории информации 2
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Клод Элвуд Шеннон Claude Elwood Shannon Гениальный американский математик и электротехник, один из создателей математической теории информации 2
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 2
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 2
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 2 Собственная информация и избыточность (цифровые сигналы) - энтропия сигнала Х (математическое ожидание собственной информации). Пример: xj = j 0 90 p(xj) 0, 10 0, 60 I(xj) 3, 32 0, 74 180 0, 18 2, 47 270 0, 12 3, 06 H(X) = - 0, 1 log 0, 1 - 0, 6 log 0, 6 - 0, 18 log 0, 18 - 0, 12 log 0, 12 = 1, 587 бит. H(x) Hmax = logm
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 2 Собственная информация и избыточность (цифровые сигналы) - энтропия сигнала Х (математическое ожидание собственной информации). Пример: xj = j 0 90 p(xj) 0, 10 0, 60 I(xj) 3, 32 0, 74 180 0, 18 2, 47 270 0, 12 3, 06 H(X) = - 0, 1 log 0, 1 - 0, 6 log 0, 6 - 0, 18 log 0, 18 - 0, 12 log 0, 12 = 1, 587 бит. H(x) Hmax = logm
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 3 Собственная информация и избыточность (цифровые сигналы) - последовательность длины n, состоящая из m-ичных символов
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 3 Собственная информация и избыточность (цифровые сигналы) - последовательность длины n, состоящая из m-ичных символов
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 3 Собственная информация и избыточность (цифровые сигналы) Избыточность сигнала или где L – среднее количество символов в сигнале.
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 3 Собственная информация и избыточность (цифровые сигналы) Избыточность сигнала или где L – среднее количество символов в сигнале.
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 4 Теория информации. Кодирование источника Пример кодовой таблицы xj p(xj) Кодовые lj слова a 0, 2 101 3 б 0, 5 010 3 в 0, 1 0 1 г 0, 1 1001 4 д 0, 1 110000 6 Равенство L = Lmin возможно лишь, если для всех xj имеем
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 4 Теория информации. Кодирование источника Пример кодовой таблицы xj p(xj) Кодовые lj слова a 0, 2 101 3 б 0, 5 010 3 в 0, 1 0 1 г 0, 1 1001 4 д 0, 1 110000 6 Равенство L = Lmin возможно лишь, если для всех xj имеем
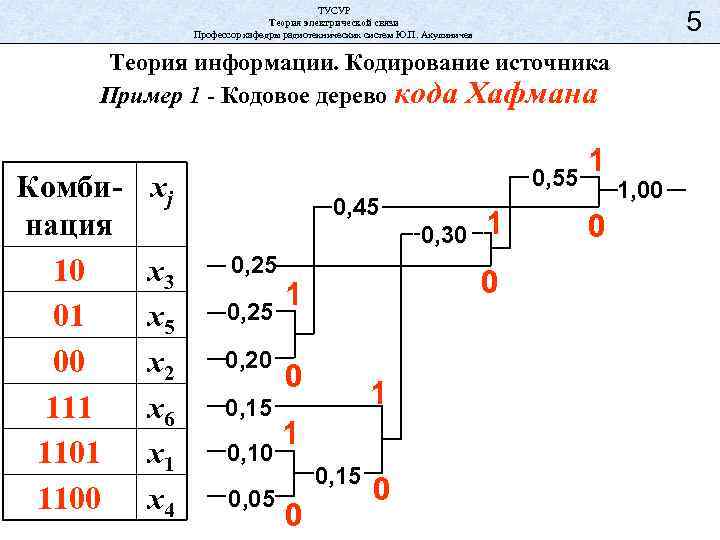 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 5 Теория информации. Кодирование источника Пример 1 - Кодовое дерево кода Хафмана Комбинация 10 01 00 111 1100 0, 55 xj 0, 45 0, 30 x 3 x 5 x 2 x 6 x 1 x 4 0, 25 0, 20 0, 15 0, 10 0, 05 0 1 1 0, 15 0 1 0 1, 00
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 5 Теория информации. Кодирование источника Пример 1 - Кодовое дерево кода Хафмана Комбинация 10 01 00 111 1100 0, 55 xj 0, 45 0, 30 x 3 x 5 x 2 x 6 x 1 x 4 0, 25 0, 20 0, 15 0, 10 0, 05 0 1 1 0, 15 0 1 0 1, 00
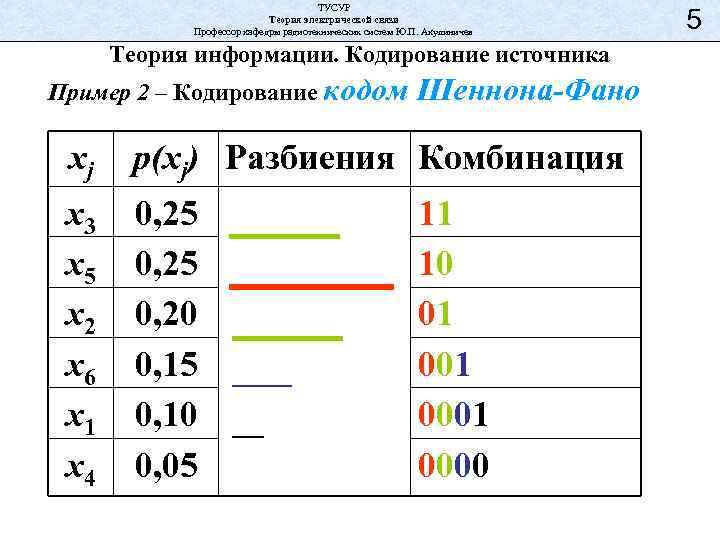 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Теория информации. Кодирование источника Пример 2 – Кодирование кодом Шеннона-Фано xj p(xj) Разбиения Комбинация x 3 x 5 x 2 x 6 x 1 x 4 0, 25 0, 20 0, 15 0, 10 0, 05 11 10 01 0001 0000 5
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Теория информации. Кодирование источника Пример 2 – Кодирование кодом Шеннона-Фано xj p(xj) Разбиения Комбинация x 3 x 5 x 2 x 6 x 1 x 4 0, 25 0, 20 0, 15 0, 10 0, 05 11 10 01 0001 0000 5
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Пример кодирования кодом Лемпела-Зива 6
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Пример кодирования кодом Лемпела-Зива 6
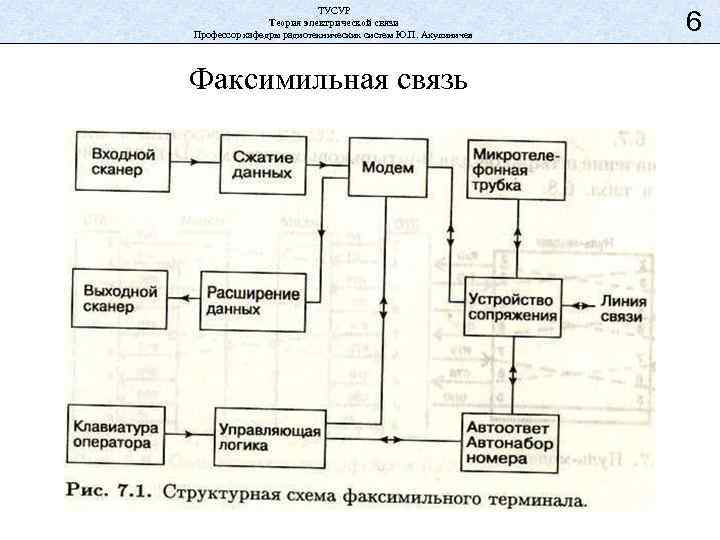 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Факсимильная связь 6
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Факсимильная связь 6
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Факсимильная связь 6
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Факсимильная связь 6
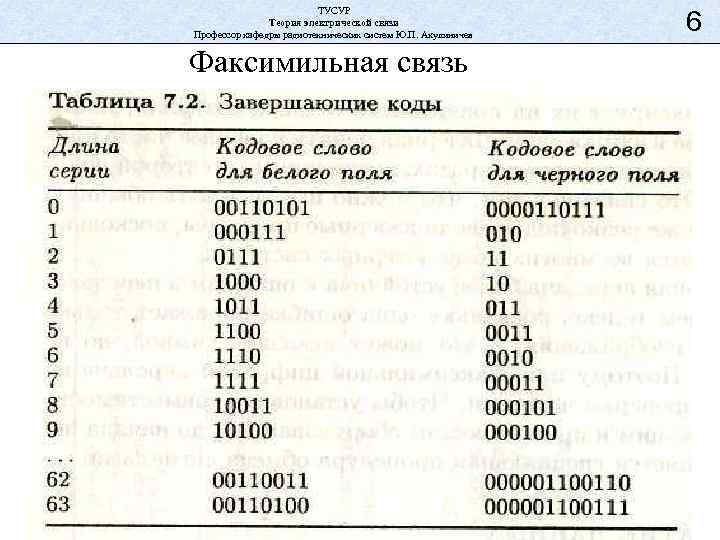 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Факсимильная связь 6
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Факсимильная связь 6
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Факсимильная связь 6
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Факсимильная связь 6
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Факсимильная связь 6
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Факсимильная связь 6
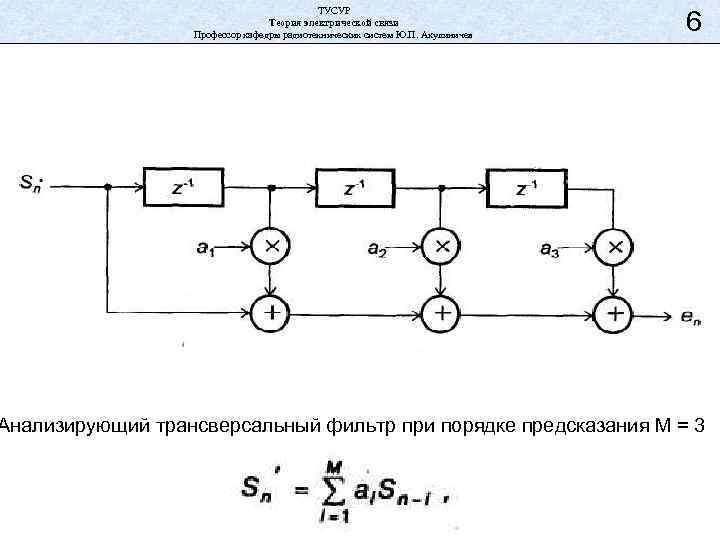 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 6 Анализирующий трансверсальный фильтр при порядке предсказания М = 3
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 6 Анализирующий трансверсальный фильтр при порядке предсказания М = 3
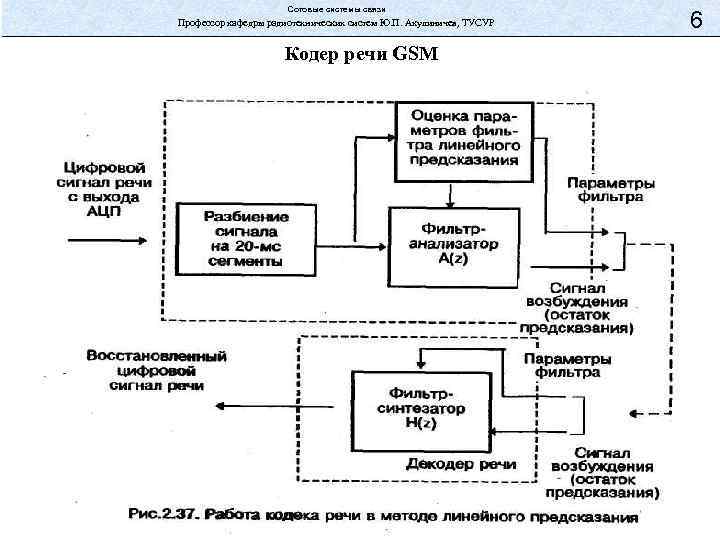 Сотовые системы связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев, ТУСУР Кодер речи GSM 6
Сотовые системы связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев, ТУСУР Кодер речи GSM 6
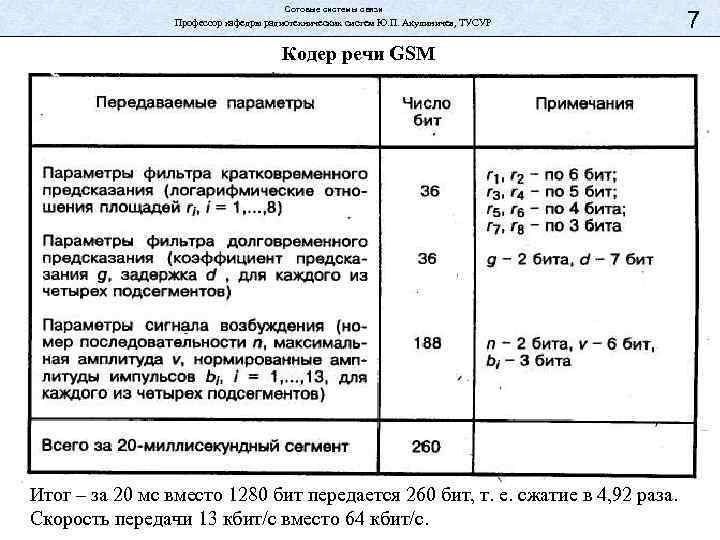 Сотовые системы связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев, ТУСУР Кодер речи GSM Итог – за 20 мс вместо 1280 бит передается 260 бит, т. е. сжатие в 4, 92 раза. Скорость передачи 13 кбит/с вместо 64 кбит/с. 7
Сотовые системы связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев, ТУСУР Кодер речи GSM Итог – за 20 мс вместо 1280 бит передается 260 бит, т. е. сжатие в 4, 92 раза. Скорость передачи 13 кбит/с вместо 64 кбит/с. 7
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Взаимная информация Количество информации, извлекаемой получателем из принятого сигнала yk, когда в действительности передавалось сообщение xj Свойство симметрии: 7
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Взаимная информация Количество информации, извлекаемой получателем из принятого сигнала yk, когда в действительности передавалось сообщение xj Свойство симметрии: 7
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Взаимная информация В канале без помех Средняя взаимная информация между X и Y 7
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Взаимная информация В канале без помех Средняя взаимная информация между X и Y 7
 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 8 Пропускная способность канала это наибольшая возможная в этом канале скорость передачи информации (бит/символ или бит/с) при заданных ограничениях на значения ряда его физических параметров. Пропускная способность m-ичного канала без помех:
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 8 Пропускная способность канала это наибольшая возможная в этом канале скорость передачи информации (бит/символ или бит/с) при заданных ограничениях на значения ряда его физических параметров. Пропускная способность m-ичного канала без помех:
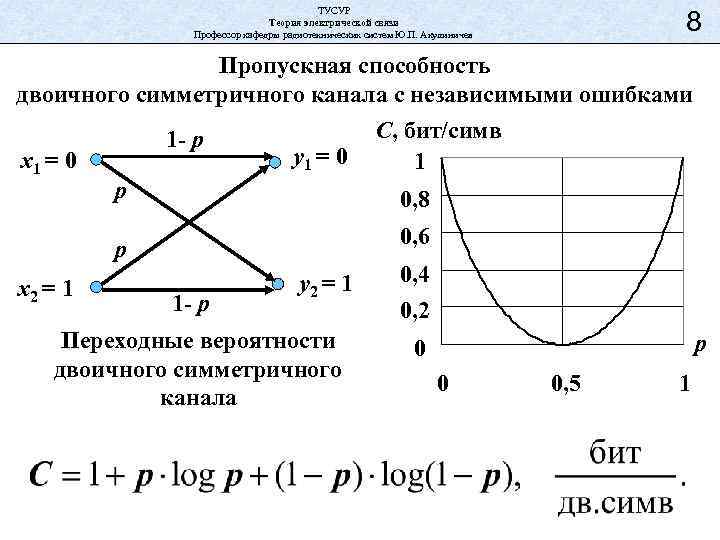 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 8 Пропускная способность двоичного симметричного канала с независимыми ошибками x 1 = 0 1 - p y 1 = 0 p 0, 8 0, 6 p x 2 = 1 C, бит/симв 1 1 - p y 2 = 1 Переходные вероятности двоичного симметричного канала 0, 4 0, 2 p 0 0 0, 5 1
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 8 Пропускная способность двоичного симметричного канала с независимыми ошибками x 1 = 0 1 - p y 1 = 0 p 0, 8 0, 6 p x 2 = 1 C, бит/симв 1 1 - p y 2 = 1 Переходные вероятности двоичного симметричного канала 0, 4 0, 2 p 0 0 0, 5 1
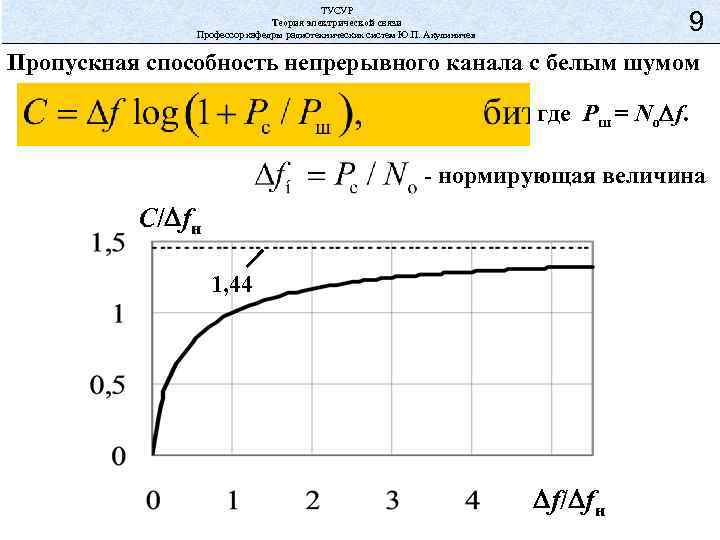 ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 9 Пропускная способность непрерывного канала с белым шумом где Pш = No f. - нормирующая величина C/ fн 1, 44 f/ fн
ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 9 Пропускная способность непрерывного канала с белым шумом где Pш = No f. - нормирующая величина C/ fн 1, 44 f/ fн


