ТУСУР Теория электрической связи Часть 3 Профессор кафедры

ТУСУР Теория электрической связи Часть 3 Профессор кафедры радиотехнических систем, д. т. н. Юрий Павлович Акулиничев

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Кодирование для обнаружения и исправления ошибок Метод контрольных сумм 145825511234 14582551124 1000101011110001011 2

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 2 Ричард Хэмминг был первым, кто предложил конструктивный метод построения кодов с избыточностью и простым декодированием. Его труд предопределил направление большинства работ в этой области, последовавших позже.

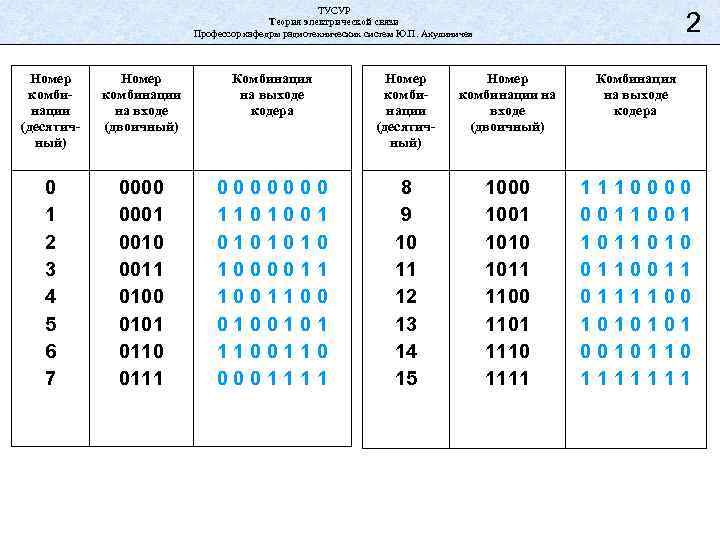ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 2 Номер комбинации (десятичный) Номер комбинации на входе (двоичный) Комбинация на выходе кодера 0 1 2 3 4 5 6 7 0000 0001 0010 0011 0100 0101 0110 0111 0000000 1101001 0101010 1000011 1001100 0100101 1100110 0001111 8 9 10 11 12 13 14 15 1000 1001 1010 1011 1100 1101 1110 1111 1110000 0011001 1011010 0110011 0111100 1010101 0010110 1111111

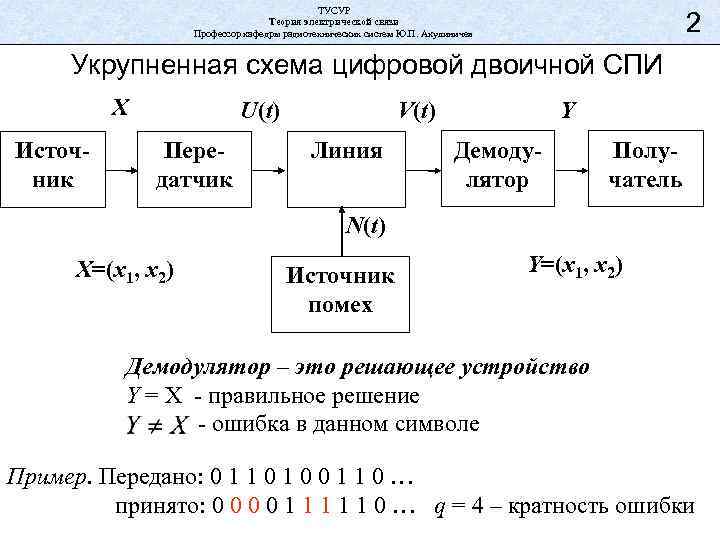ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 2 Укрупненная схема цифровой двоичной СПИ X Источник U(t) Передатчик V(t) Линия Y Демодулятор Получатель N(t) X=(x 1, x 2) Источник помех Y=(x 1, x 2) Демодулятор – это решающее устройство Y = X - правильное решение - ошибка в данном символе Пример. Передано: 0 1 1 0 … принято: 0 0 1 1 1 0 … q = 4 – кратность ошибки

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 2 Блочные корректирующие коды где W – вес комбинации. Расстояние Хэмминга Вектор ошибки e, где x и y – комбинации на входе и выходе линии. Кратность ошибки q , y=x+e q = W(e) = W(x+y) = dxy В канале с независимыми ошибками В обычных условиях наиболее вероятно появление ошибок малых кратностей (чаще всего q = 0, реже q = 1 и т. д. )

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Блочные корректирующие коды Пример кодовой таблицы (n=6) Буква Комбинация а 000000 б 000111 в 111000 г 111111 Можно гарантированно обнаруживать любые ошибки кратности Можно гарантированно исправить любые ошибки кратности 3

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Линейные блочные (n, k)-коды k - количество информационных символов (на входе) n - количество символов в комбинации на выходе R = n - k - количество проверочных символов - количество комбинаций в кодовой таблице Самый простой - код с проверкой на чётность (n, n-1) 4

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Линейные блочные (n, k)-коды Пример: (4, 3)-код Вход Выход 000 001 010 011 100 101 110 111 0000 0011 0101 0110 1001 1010 1100 1111 Примеры комбинаций на входе декодера и выносимых решений 1000 – есть хотя бы одна ошибка; 1111 – скорее всего, ошибок нет; 1100 – скорее всего, ошибок нет; 0111 – есть хотя бы одна ошибка; 1000 – есть хотя бы одна ошибка; 0000 – скорее всего, ошибок нет; 5

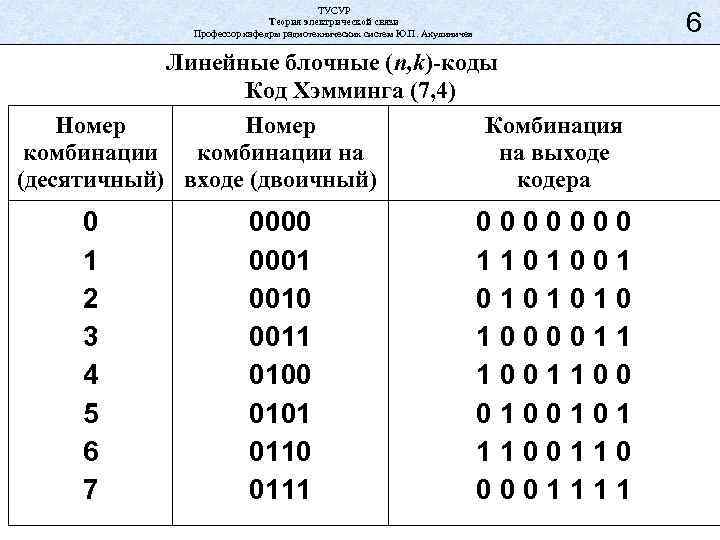ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 6 Линейные блочные (n, k)-коды Код Хэмминга (7, 4) Номер Комбинация комбинации на на выходе (десятичный) входе (двоичный) кодера 0 1 2 3 4 5 6 7 0000 0001 0010 0011 0100 0101 0110 0111 0000000 1101001 0101010 1000011 1001100 0100101 1100110 0001111

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 7 Линейные блочные (n, k)-коды Код Хэмминга (7, 4) - продолжение Номер комбинации (десятичный) Номер комбинации на входе (двоичный) Комбинация на выходе кодера 8 9 10 11 12 13 14 15 1000 1001 1010 1011 1100 1101 1110 1111 1110000 0011001 1011010 0110011 0111100 1010101 0010110 1111111

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 8 Линейные блочные (n, k)-коды Код Хэмминга (7, 4) Номер комбинации (дес. ) Номер комбинации (дв. ) – вход Комбинация на выходе кодера 0 1 2 3 4 5 6 7 0000 0001 0010 0011 0100 0101 0110 0111 0000000 1101001 0101010 1000011 1001100 0100101 1100110 0001111 Номер комби- комбинации (дес. ) (дв. ) – вход 8 9 10 11 12 13 14 15 1000 1001 1010 1011 1100 1101 1110 1111 Комбинация на выходе кодера 1110000 0011001 1011010 0110011 0111100 1010101 0010110 1111111

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 9 Линейные блочные (n, k)-коды Код Хэмминга (7, 4) Номер комбинации (дес. ) Номер комбинации (дв. ) – вход Комбинация на выходе кодера 0 1 2 3 4 5 6 7 0000 0001 0010 0011 0100 0101 0110 0111 0000000 1101001 0101010 1000011 1001100 0100101 1100110 0001111 Номер комби- комбинации (дес. ) (дв. ) – вход 8 9 10 11 12 13 14 15 1000 1001 1010 1011 1100 1101 1110 1111 Комбинация на выходе кодера 1110000 0011001 1011010 0110011 0111100 1010101 0010110 1111111

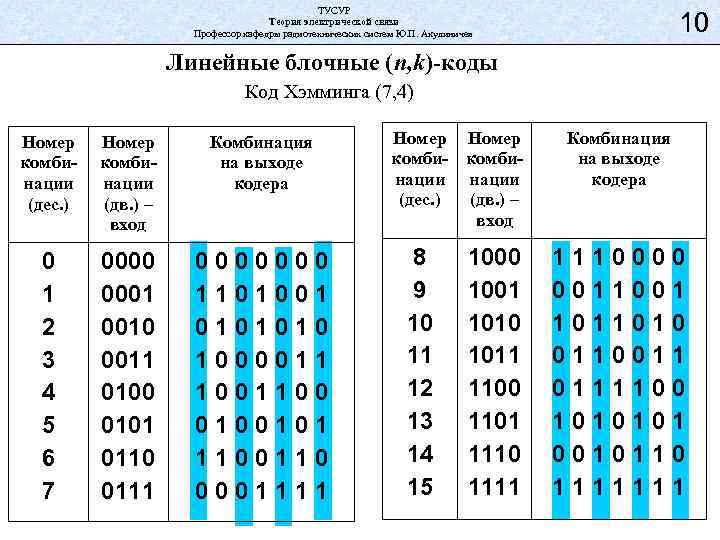ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 10 Линейные блочные (n, k)-коды Код Хэмминга (7, 4) Номер комбинации (дес. ) Номер комбинации (дв. ) – вход Комбинация на выходе кодера 0 1 2 3 4 5 6 7 0000 0001 0010 0011 0100 0101 0110 0111 0000000 1101001 0101010 1000011 1001100 0100101 1100110 0001111 Номер комби- комбинации (дес. ) (дв. ) – вход 8 9 10 11 12 13 14 15 1000 1001 1010 1011 1100 1101 1110 1111 Комбинация на выходе кодера 1110000 0011001 1011010 0110011 0111100 1010101 0010110 1111111

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Линейные блочные (n, k)-коды. 11 Код Хэмминга (7, 4) Схема проверок на чётность для кода Хэмминга (7, 4) s 1 s 2 s 3 s 4 s 5 s 6 s 7 Первая Вторая Третья Проверочная матрица 0001111 H 0110011 1010101

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Линейные блочные (n, k)-коды. Примеры комбинаций на входе декодера и выносимых решений, полагая, что ошибка одиночная: 1000000 – есть ошибка (скорее всего, в первом символе); 0001111 – скорее всего, ошибок нет; 1110000 – скорее всего, ошибок нет; 0111101 – есть ошибка (скорее всего, в седьмом символе); 1001111 – есть ошибка (скорее всего, в первом символе); 0000000 – скорее всего, ошибок нет; 12 Код Хэмминга (7, 4) Таблица соответствия вектора ошибки e и синдрома c e c 1000000 0100000 0010000 0001000 0000100 0000010 0000001 010 011 100 101 110 111

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Линейные блочные (n, k)-коды. Код Хэмминга (7, 4) Информационные и проверочные символы в комбинациях кода (7, 4) S 3 Проверочная матрица S 5 S 6 S 7 0001111 H 0110011 1010101 Первая Вторая Третья Правила кодирования: 1) входящие 4 информационных символа – на позиции S 3; S 5; S 6; S 7; 2) затем S 4=S 5+S 6+S 7 S 2=S 3+S 6+S 7 S 1=S 3+S 5+S 7 13 Примеры комбинаций на входе и выходе кодера: 0000 0001 0010 0011 0100 0101 0000000 1101001 0101010 1000011 1001100 0100101

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 14 Линейный блочный (5, 2)-код n – количество символов в комбинации, в том числе: k - количество информационных символов, R = n - k - количество проверочных символов. 2 n – общее количество комбинаций; 2 k – количество разрешенных комбинаций. Схема проверок на чётность для кода (5, 2) Проверочная матрица Первая Вторая Третья

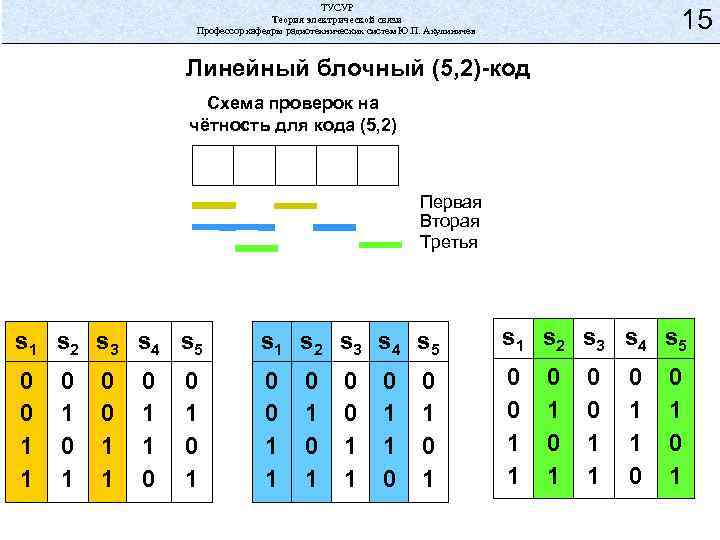ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 15 Линейный блочный (5, 2)-код Схема проверок на чётность для кода (5, 2) Первая Вторая Третья s 1 s 2 s 3 s 4 s 5 0 0 1 1 0 1 0 1 0 0 1 1 0 0 1 0 1 0 1 0 0 1

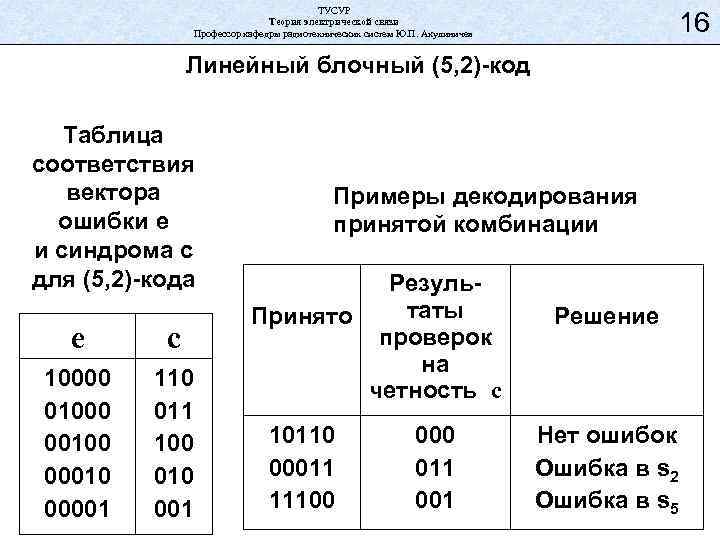ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 16 Линейный блочный (5, 2)-код Таблица соответствия вектора ошибки e и синдрома c для (5, 2)-кода e c 10000 01000 00100 00010 00001 110 011 100 010 001 Примеры декодирования принятой комбинации Результаты Принято проверок на четность c 10110 00011 11100 011 001 Решение Нет ошибок Ошибка в s 2 Ошибка в s 5

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 17 Линейный блочный (5, 2)-код Убедиться, что код способен: -- обнаружить наличие любых одиночных и двойных ошибок; -- исправить любую одиночную ошибку. Параметры оптимальных кодов с такими же свойствами: (7, 4), (15, 11), (31, 26), … , (1023, 1013), (2047, 2036), …. Они называются кодами Хэмминга. Для них n=2 r-1.

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 18 Линейные блочные (n, k)-коды Для любого линейного блочного кода существуют: -- проверочная матрица H (r строк и n столбцов), -- производящая матрица G (k строк и n столбцов). Фундаментальные свойства: Для (5, 2)-кода: a s 00 01 10 11 00000 010110 11101

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 19 Линейные блочные (n, k)-коды. Способы кодирования: 1) выполняя условие т. е. 2) по формуле Способы декодирования принятой комбинации 1) с вычислением синдрома , т. е. 2) по матрице G, т. е. путем повторного кодирования принятых информационных символов и сравнения проверочных символов :

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Линейные блочные (n, k)-коды. Циклические коды Описание комбинаций с помощью полиномов Особые правила: 1) суммирование по модулю 2. Пример: x + x = x(1 + 1) = 0, 2) при умножении принимать Пример: 20

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Циклические коды Способы кодирования и декодирования конкретным циклическим кодом полностью определяются его производящим (порождающим, генераторным) полиномом степени r Фундаментальное свойство циклического кода: Полином степени k называется проверочным полиномом данного циклического кода Фундаментальное свойство: 21

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Пример: циклический (7, 4)-код, dкод=3 Из таблиц берем производящий полином Вычисление проверочного полинома h(x) x 7+1 x 3+x+1 + x 7+x 5+x 4 x 4+x 2+x+1 x 5+x 4+1 + 5 3 2 x +x +x x 4+x 3+x 2+1 + x 4+x 2+x x 3+x+1 + 3 x +x+1 0 22

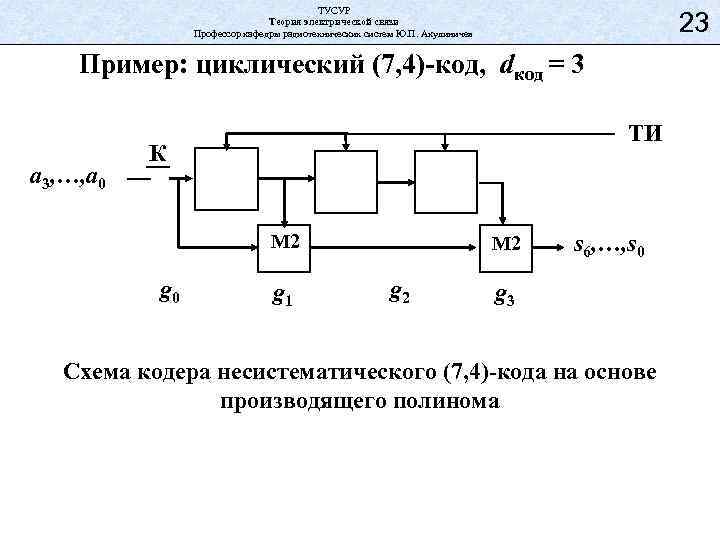ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 23 Пример: циклический (7, 4)-код, dкод = 3 a 3, …, a 0 ТИ К M 2 g 0 g 1 M 2 g 2 s 6, …, s 0 g 3 Схема кодера несистематического (7, 4)-кода на основе производящего полинома

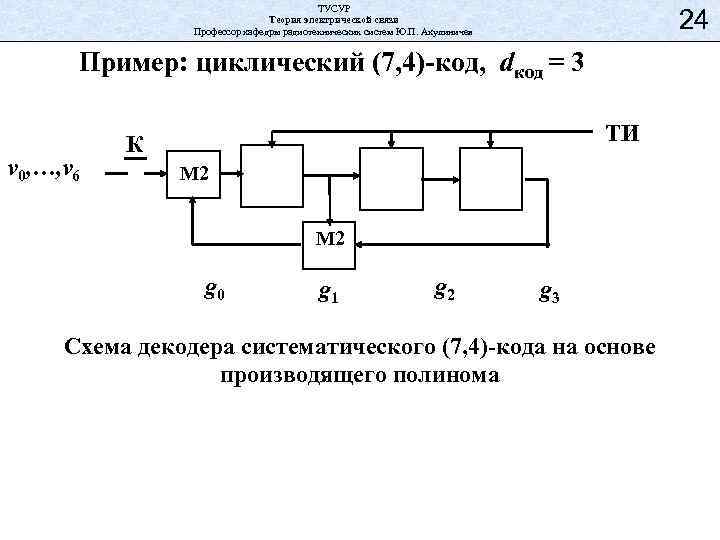ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 24 Пример: циклический (7, 4)-код, dкод = 3 v 0, …, v 6 ТИ К M 2 g 0 g 1 g 2 g 3 Схема декодера систематического (7, 4)-кода на основе производящего полинома

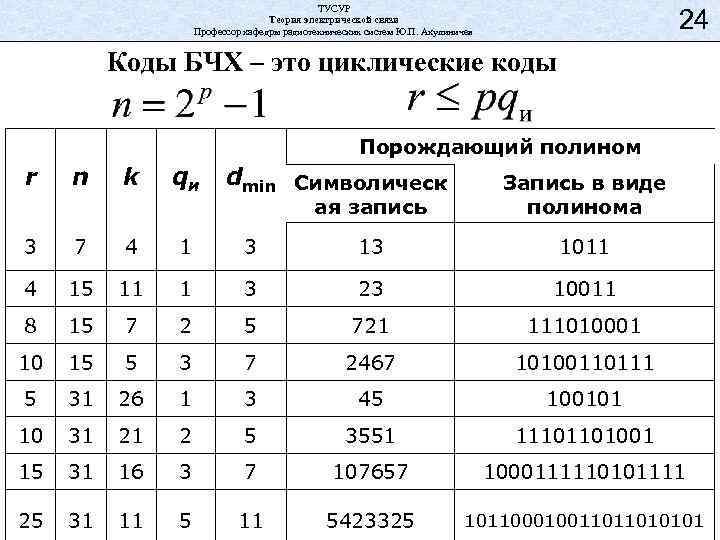ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 24 Коды БЧХ – это циклические коды Порождающий полином r n k qи dmin Символическ ая запись Запись в виде полинома 3 7 4 1 3 13 1011 4 15 11 1 3 23 10011 8 15 7 2 5 721 111010001 10 15 5 3 7 2467 10100110111 5 31 26 1 3 45 100101 10 31 21 2 5 3551 11101101001 15 31 16 3 7 107657 1000111110101111 25 31 11 5423325 101100010011011010101

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 24 Код Рида-Соломона Недвоичный циклический код, использующий М-ичные символы, где М = 2 m. где t – количество ошибочных битов в символе, которое может исправить код. Вместо этого может исправить r стираний. Хорош для исправления пакетов ошибок.

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 25 Применение канала переспроса (прямой канал – двоичный, симметричный, с независимыми ошибками; р – битовая вероятность ошибки) СПИ без канала переспроса (для сравнения)

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 26 Применение канала переспроса в прямом канале – код Xэмминга (127, 120). Пример: Вероятность повторной передачи Битовая вероятность ошибки на выходе декодера

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 27 Свёрточные коды Параметры: k/n - степень кодирования, К - длина кодового ограничения, N = К – число разрядов в регистре сдвига. Инф. биты 1 2 …. k M 21 MUX M 22 M 2 n Общая схема кодера сверточного кода со степенью кодирования k/n

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 28 Свёрточные коды. Схема кодера Пример: систематический свёрточный код, степень кодирования k/n = 1/3, избыточность R = 2/3, длина кодового ограничения К = 3. Инф. биты MUX M 2 Выход M 2

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Свёрточные коды Пример: систематический свёрточный код, степень кодирования k/n=1/3, избыточность R=2/3, длина кодового ограничения К=3. Последовательности символов, участвующие в пороговом декодировании Принятые и и и п 1 п 1 п 1 п 2 п 2 п 2 Новые п 1 п 1 п 1 п 2 п 2 п 2 29

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Перемежение Перестановка символов из разных кодовых комбинаций на выходе кодера. Применяется в случае, когда в канале возможно появление пакетов ошибок, например вследствие многолучевости. Пакет ошибок – это интервал времени, в течение которого резко возрастает вероятность появления ошибок (ошибки происходят особенно часто). Пакеты ошибок обычно возникают вследствие временного уменьшения отношения сигнал/шум во время глубоких замираний сигнала. 29

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 30 Шифрование Цели шифрования: 1) обеспечение конфиденциальности, то есть воспрепятствование раскрытию смысла сообщения, перехваченного незаконным пользователем; 2) аутентификация, то есть предотвращение передачи по сети сообщений, незаконно внедрённых в открытый канал (см. выше); 3) обеспечение электронной подписи, то есть убедительной гарантии того, что данное сообщение было передано конкретным лицом и ни кем иным; 4) идентификация, то есть проверка того, что оборудование, используемое для передачи, соответствует стандарту, не находится в розыске и т. п.

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Шифрование Ключ (К) – это набор символов и численных значений, определяющих конкретное шифрующее преобразование из семейства криптографических преобразований. Возможны блочное шифрование и поточное шифрование. 30

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 31 Симметричные системы шифрования Система перестановок Применение метода букв алфавита скремблирования Буква Замена X 01101001… алфавита ПСП 0 1 1 1 0 0 … Шифратор а д Y 00110101… б г Y 00110101… в в Дешифратор ПСП 0 1 1 1 0 0 … г а Z 01101001… д л л б

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Асимметричные системы шифрования (с открытым ключом) Метод RSA (авторы Rivest – Shamiz - Adleman) Генерирование ключей: 1) задаются два больших положительных целых простых числа р и q и произвольное большое число d; 2) вычисляется n = pq и решается уравнение относительно неизвестного целого числа e, где amodb обозначает остаток от деления целого числа a на целое число b; 3) пара чисел (e, n) – это открытый ключ, а (d, n) - это секретный ключ. 32

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Асимметричные системы шифрования (с открытым ключом) Метод RSA (авторы Rivest – Shamiz - Adleman) Шифрование Дешифрование 32

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 32 Метод RSA (пример) Попробуем на маленьких числах. Установим р = 3, q = 7. Тогда n = р*q = 21. Выбираем d как 5. Из формулы (e*5) mod 12 = 1 вычисляем e = 17. Открытый ключ 17, 21, секретный -- 5, 21. Зашифруем последовательность (2, 3, 4, 5): C(2) = 217 mod 21 = 11 C(3) = 317 mod 21 = 12 C(4) = 417 mod 21 = 16 C(5) = 517 mod 21 = 17 Криптотекст – 11, 12, 16, 17. Localhost. ru

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев 32 Метод RSA (пример) Открытый ключ 17, 21, секретный -- 5, 21. Проверим расшифровкой: M(2) = 115 mod 21 = 2 M(3) = 125 mod 21 = 3 M(4) = 165 mod 21 = 4 M(5) = 175 mod 21 = 5 Как видим, результат совпал. Localhost. ru

ТУСУР Теория электрической связи Профессор кафедры радиотехнических систем Ю. П. Акулиничев Метод RSA (пример 2) Установим р = 3, q = 5. Выбираем d как 5. 32