0311530f17b135ad010b47ba31d35cf0.ppt
- Количество слайдов: 25

Turbulence Energetics in Stably Stratified Atmospheric Flows Sergej Zilitinkevich Division of Atmospheric Sciences, Department of Physical Sciences University of Helsinki and Finnish Meteorological Institute Helsinki, Finland Tov Elperin, Nathan Kleeorin, Igor Rogachevskii Department of Mechanical Engineering The Ben-Gurion University of the Negev Beer-Sheva, Israel Victor L’vov Department of Chemical Physics ITI Conference on Turbulence III, 12 -16 October 2008, Bertinoro, Italy
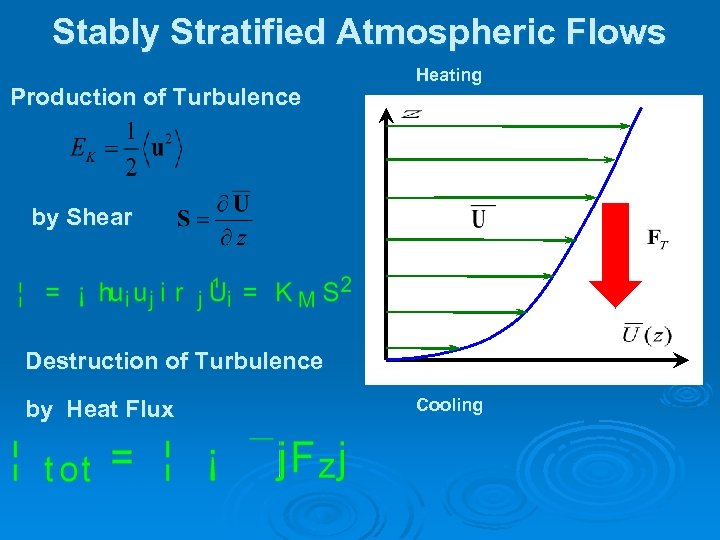
Stably Stratified Atmospheric Flows Production of Turbulence Heating by Shear Destruction of Turbulence by Heat Flux Cooling

Laminar and Turbulent Flows Laminar Boundary Layer Turbulent Boundary Layer

Boussinesq Approximation
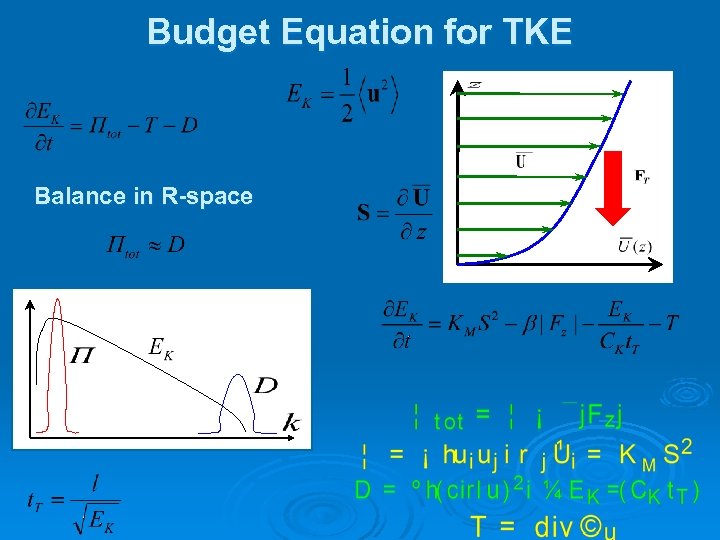
Budget Equation for TKE Balance in R-space
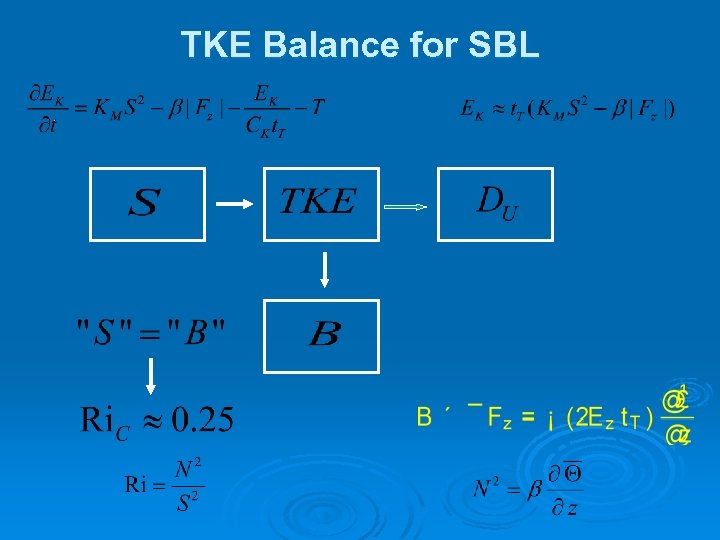
TKE Balance for SBL
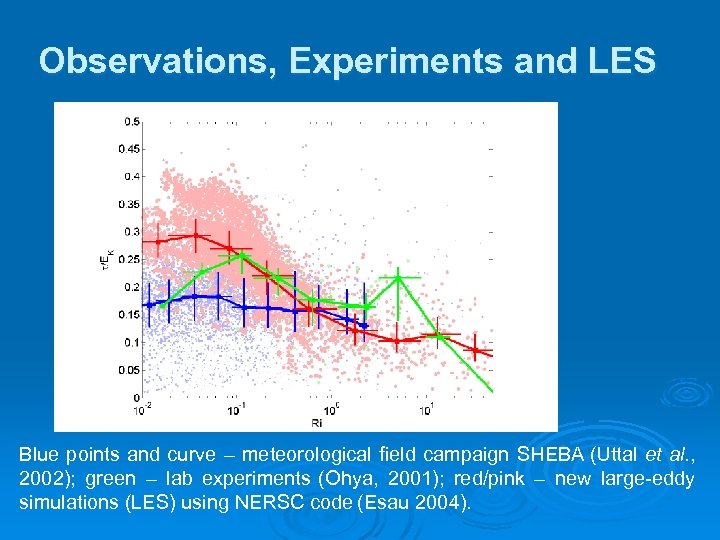
Observations, Experiments and LES Blue points and curve – meteorological field campaign SHEBA (Uttal et al. , 2002); green – lab experiments (Ohya, 2001); red/pink – new large-eddy simulations (LES) using NERSC code (Esau 2004).

Budget Equations for SBL Ø Turbulent kinetic energy: Ø Potential temperature fluctuations: Ø Flux of potential temperature :

Budget Equations for SBL

Total Turbulent Energy The turbulent potential energy: The source:

Budget Equations for SBL

Critical Richardson Number

No Critical Richardson Number Deardorff (1970)

Budget Equations for SBL
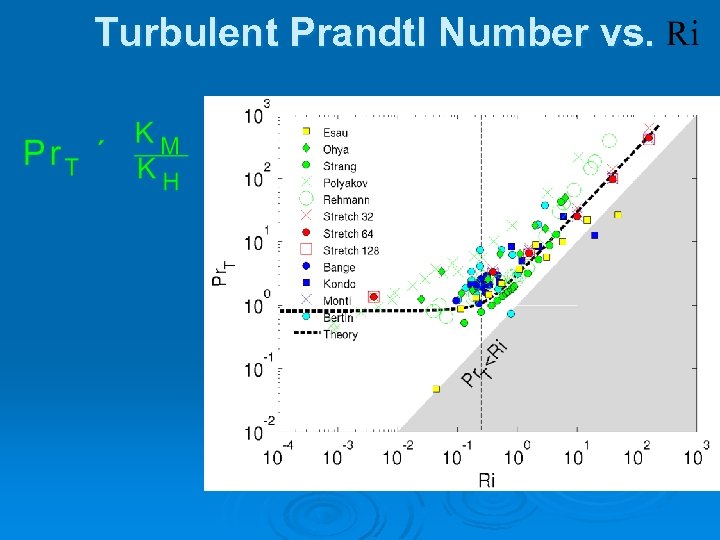
Turbulent Prandtl Number vs.

Budget Equations for SBL with Large-Scale Internal Gravity Waves
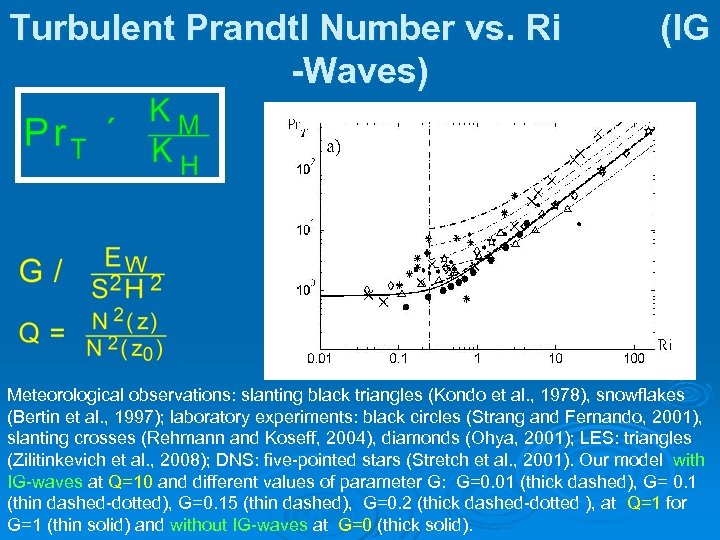
Turbulent Prandtl Number vs. Ri -Waves) (IG Meteorological observations: slanting black triangles (Kondo et al. , 1978), snowflakes (Bertin et al. , 1997); laboratory experiments: black circles (Strang and Fernando, 2001), slanting crosses (Rehmann and Koseff, 2004), diamonds (Ohya, 2001); LES: triangles (Zilitinkevich et al. , 2008); DNS: five-pointed stars (Stretch et al. , 2001). Our model with IG-waves at Q=10 and different values of parameter G: G=0. 01 (thick dashed), G= 0. 1 (thin dashed-dotted), G=0. 15 (thin dashed), G=0. 2 (thick dashed-dotted ), at Q=1 for G=1 (thin solid) and without IG-waves at G=0 (thick solid).
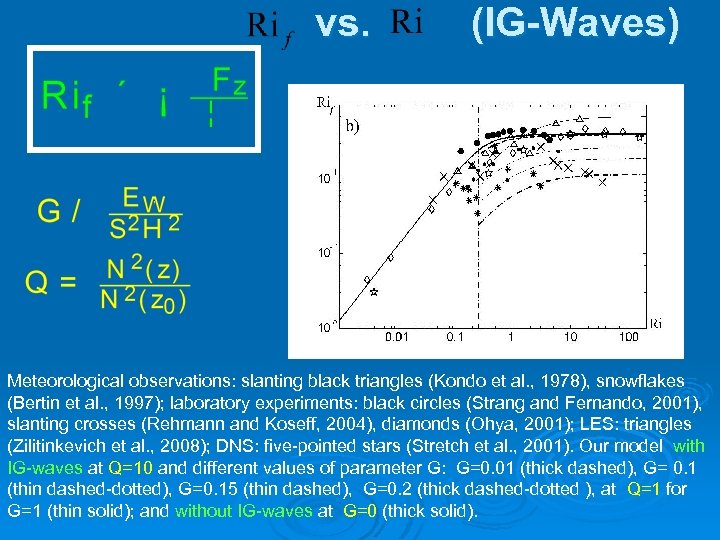
vs. (IG-Waves) Meteorological observations: slanting black triangles (Kondo et al. , 1978), snowflakes (Bertin et al. , 1997); laboratory experiments: black circles (Strang and Fernando, 2001), slanting crosses (Rehmann and Koseff, 2004), diamonds (Ohya, 2001); LES: triangles (Zilitinkevich et al. , 2008); DNS: five-pointed stars (Stretch et al. , 2001). Our model with IG-waves at Q=10 and different values of parameter G: G=0. 01 (thick dashed), G= 0. 1 (thin dashed-dotted), G=0. 15 (thin dashed), G=0. 2 (thick dashed-dotted ), at Q=1 for G=1 (thin solid); and without IG-waves at G=0 (thick solid).
![vs. Ri (IG-Waves) Meteorological observations: squares [CME, Mahrt and Vickers (2005)], circles [SHEBA, Uttal vs. Ri (IG-Waves) Meteorological observations: squares [CME, Mahrt and Vickers (2005)], circles [SHEBA, Uttal](https://present5.com/presentation/0311530f17b135ad010b47ba31d35cf0/image-19.jpg)
vs. Ri (IG-Waves) Meteorological observations: squares [CME, Mahrt and Vickers (2005)], circles [SHEBA, Uttal et al. (2002)], overturned triangles [CASES-99, Poulos et al. (2002), Banta et al. (2002)], slanting black triangles (Kondo et al. , 1978), snowflakes (Bertin et al. , 1997); laboratory experiments: black circles (Strang and Fernando, 2001), slanting crosses (Rehmann and Koseff, 2004), diamonds (Ohya, 2001); LES: triangles (Zilitinkevich et al. , 2008); DNS: five-pointed stars (Stretch et al. , 2001). Our model with IG-waves at Q=10 and different values of parameter G: G=0. 01 (thick dashed), G=0. 04 (thin dashed), G= 0. 1 (thin dashed-dotted), G=0. 3 (thick dashed-dotted), at Q=1 for G=0. 5 (thin solid); and without IG-waves at G=0 (thick solid).
![vs. Ri (IG-Waves) Meteorological observations: squares [CME, Mahrt and Vickers (2005)], circles [SHEBA, Uttal vs. Ri (IG-Waves) Meteorological observations: squares [CME, Mahrt and Vickers (2005)], circles [SHEBA, Uttal](https://present5.com/presentation/0311530f17b135ad010b47ba31d35cf0/image-20.jpg)
vs. Ri (IG-Waves) Meteorological observations: squares [CME, Mahrt and Vickers (2005)], circles [SHEBA, Uttal et al. (2002)], overturned triangles [CASES-99, Poulos et al. (2002), Banta et al. (2002)], slanting black triangles (Kondo et al. , 1978), snowflakes (Bertin et al. , 1997); laboratory experiments: black circles (Strang and Fernando, 2001), slanting crosses (Rehmann and Koseff, 2004), diamonds (Ohya, 2001); LES: triangles (Zilitinkevich et al. , 2008); DNS: five-pointed stars (Stretch et al. , 2001). Our model with IG-waves at Q=10 and different values of parameter G: G=0. 001 (thin dashed), G=0. 005 (thick dashed), G= 0. 01 (thin dashed-dotted), G=0. 05 (thick dashed-dotted), at Q=1 for G=0. 1 (thin solid); and without IG-waves at G=0 (thick solid).

vs. (IG-Waves) Meteorological observations: overturned triangles [CASES-99, Poulos et al. (2002), Banta et al. (2002)]; laboratory experiments: diamonds (Ohya, 2001); LES: triangles (Zilitinkevich et al. , 2008). Our model with IG-waves at Q=10 and different values of parameter G: G=0. 2 (thick dashed-dotted), at Q=1 for G=1 (thin solid); and without IGwaves at G=0 (thick solid for ) and (thick dashed for ).
![Anisotropy vs. (IG-Waves) Meteorological observations: squares [CME, Mahrt and Vickers (2005)], circles [SHEBA, Uttal Anisotropy vs. (IG-Waves) Meteorological observations: squares [CME, Mahrt and Vickers (2005)], circles [SHEBA, Uttal](https://present5.com/presentation/0311530f17b135ad010b47ba31d35cf0/image-22.jpg)
Anisotropy vs. (IG-Waves) Meteorological observations: squares [CME, Mahrt and Vickers (2005)], circles [SHEBA, Uttal et al. (2002)], overturned triangles [CASES-99, Poulos et al. (2002), Banta et al. (2002)], slanting black triangles (Kondo et al. , 1978), snowflakes (Bertin et al. , 1997); laboratory experiments: black circles (Strang and Fernando, 2001), slanting crosses (Rehmann and Koseff, 2004), diamonds (Ohya, 2001); LES: triangles (Zilitinkevich et al. , 2008); DNS: five-pointed stars (Stretch et al. , 2001). Our model with IG-waves at Q=10 and different values of parameter G: G= 0. 01 (thick dashed), G=0. 1 (thin dasheddotted), G=0. 2 (thin dashed), G=0. 3 (thick dashed-dotted), at Q=1 for G=1 (thin solid); and without IG-waves at G=0 (thick solid).

References Ø Elperin, T. , Kleeorin, N. , Rogachevskii, I. , and Zilitinkevich, S. 2002 Formation of large-scale semi-organized structures in turbulent convection. Phys. Rev. E, 66, 066305 (1 --15) Ø Elperin, T. , Kleeorin, N. , Rogachevskii, I. , and Zilitinkevich, S. 2006 Tangling turbulence and semi-organized structures in convective boundary layers. Boundary Layer Meteorology, 119, 449 -472. Ø Zilitinkevich, S. , Elperin, T. , Kleeorin, N. , and Rogachevskii, I, 2007 Energy- and flux-budget (EFB) turbulence closure model for stably stratified flows. Boundary Layer Meteorology, Part 1: steady-state homogeneous regimes. Boundary Layer Meteorology, 125, 167 -191. Ø Zilitinkevich S. , Elperin T. , Kleeorin N. , Rogachevskii I. , Esau I. , Mauritsen T. and Miles M. , 2008, Turbulence energetics in stably stratified geophysical flows: strong and weak mixing regimes. Quarterly Journal of Royal Meteorological Society, 134, 793 -799.

Conclusions Ø Budget equation for the total turbulent energy (potential and kinetic) plays a crucial role for analysis of SBL flows. Ø Explanation for no critical Richardson number. Ø Reasonable Ri-dependencies of the turbulent Prandtl number, the anisotropy of SBL turbulence, the normalized heat flux and TKE which follow from the developed theory. Ø The scatter of observational, experimental, LES and DNS data in SBL are explained by effects of large-scale internal gravity waves on SBL-turbulence.

THE END
0311530f17b135ad010b47ba31d35cf0.ppt