Turbomachinery Lecture 4 a — Pi Theorem

Turbomachinery Lecture 4 a - Pi Theorem - Pipe Flow Similarity - Flow, Head, Power Coefficients - Specific Speed 1

Introduction to Dimensional Analysis • Thus far course has shown elementary fluid mechanics – now one can appreciate Dimensional Analysis • Dimensional Analysis – Identifies significant parameters in a process not completely understood. – Useful in analyzing experimental data. – Permits investigation of full size machine by testing smaller version – Predicts consequences of off-design operation – Useful in preliminary design studies for sizing machine for optimal performance – Useful in sizing pumps & blowers based on performance maps • Geometric similarity: assumes all linear dimensions are in constant proportion, all angular dimensions are same 2

Dimensional Analysis Buckingham -Theorem • Basic Premise – Physical process involving dimensional parameters, Q's and f(Q) is unknown. Q 1 = f(Q 2, Q 3, . . . Qn) Group the n variables into a smaller number of dimensionless groups, each having 2 or more variables – Physical process can be expressed as: 1 = g( 2, 3, . . . n-k) 3

Dimensional Analysis Buckingham -Theorem • Each is a product of the primary variables, Q's raised to various exponents so that 's are dimensionless. where n = no. primary variables k = no. physical dimensions [L, M, T] n-k = no. 's 4

Dimensional Analysis • Dimensional analysis requires – postulation of proper primary variables – judgement, foresight, good luck • Dimensional analysis cannot – give form of 1 = g( 2, . . . n-k) – prevent omission of significant Q’s – exclude an insignificant Q’s 5

Dimensional Analysis • Basic Units Mass Length Time M L T • Force is related to basic units by F=ma Force ML/T 2 6

Example: Pressure Drop in Pipe P = f(V, , , l, d, ) Pick V, , d as the 3 Q’s which will be used with each of the remaining Q’s to form the 7 - 3 = 4 terms. Pick M, L, T as the 3 primary dimensions Result 7

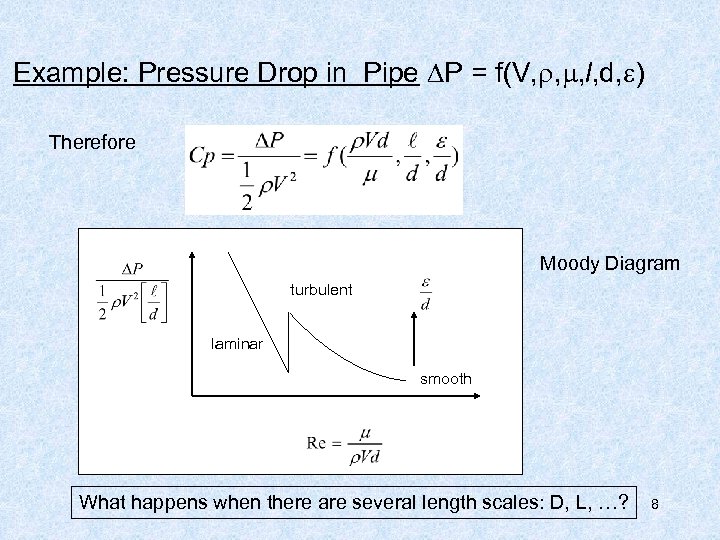
Example: Pressure Drop in Pipe P = f(V, , , l, d, ) Therefore Moody Diagram turbulent laminar smooth What happens when there are several length scales: D, L, …? 8

Dimensional Analysis of Turbomachines Primary Variables - Q’s 9

Background: Head, Power, and Viscosity Q’s • Head - work per unit mass - fluid dynamic equivalent to enthalpy • Recalling Gibbs Equation: • So head in "feet" is clearly erroneous. 10

Background: Head, Power, and Viscosity Q’s • Power - Work per unit time - Mass Flow Rate Work per unit Mass 11

Background: Head, Power, and Viscosity Q’s • Viscosity Newtonian Fluid: Shear stress Velocity gradient • Viscosity is - with units: 12

Dimensional Analysis of Turbomachines • Since there are 10 Q's & 3 Dimensions we can identify 7 's. • Each contains 4 Q's, Q 1, Q 2, Q 3, and Qn. • The parameters chosen for 1, 2 & 3 were chosen carefully. • Task is to find exponents of primary variables to make dimensionless groups. 13

Dimensional Analysis of Turbomachines • The system of equations is: 14

Dimensional Analysis of Turbomachines • Each has 3 linear equations: M L T 0 a + -a + 0 b + 1 c +0 = 0 1 b - 3 c + 3 = 0 0 b + 0 c - 1 =0 c=0 b = -3 a = -1 15

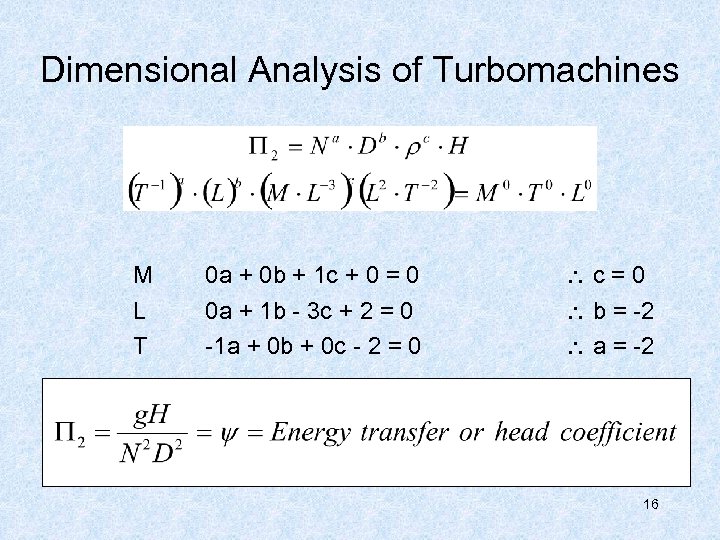
Dimensional Analysis of Turbomachines M 0 a + 0 b + 1 c + 0 = 0 c=0 L T 0 a + 1 b - 3 c + 2 = 0 -1 a + 0 b + 0 c - 2 = 0 b = -2 a = -2 16

Dimensional Analysis of Turbomachines • Aside: What is meaning of H=head? – Hydraulic engineers expressure in terms of head – Static pressure at any point in a liquid at rest is, relative to pressure acting on free surface, proportional to vertical distance from point to free surface. 17

Dimensional Analysis of Turbomachines M 0 a + 0 b + 1 c + 1 = 0 c = -1 L T 0 a + 1 b - 3 c + 2 =0 -1 a + 0 b + 0 c - 3 = 0 b = -5 a = -3 18

Dimensional Analysis of Turbomachines M 0 a + 0 b + 1 c + 1 = 0 c = -1 L T 0 a + 1 b - 3 c - 1 = 0 -1 a + 0 b + 0 c - 1 = 0 b = -2 a = -1 19

Dimensional Analysis of Turbomachines M L T 0 a + 0 b + 1 c + 0 = 0 0 a + 1 b - 3 c + 1 = 0 -1 a + 0 b + 0 c - 1 = 0 c=0 b = -1 a = -1 20

Dimensional Analysis of Turbomachines M L T 0 a + 0 b + 1 c + 0 = 0 0 a + 1 b - 3 c + 1 = 0 -1 a + 0 b + 0 c + 0 = 0 c= b = -1 a= 0 21

Turbomachinery Non-Dimensional Parameters • Derived 7 s from 10 Qs in first part of class • Now ready to - develop physical significance of s - relate to traditional parameters - discuss general similitude 22

Flow Coefficient 23

Head Coefficient 24

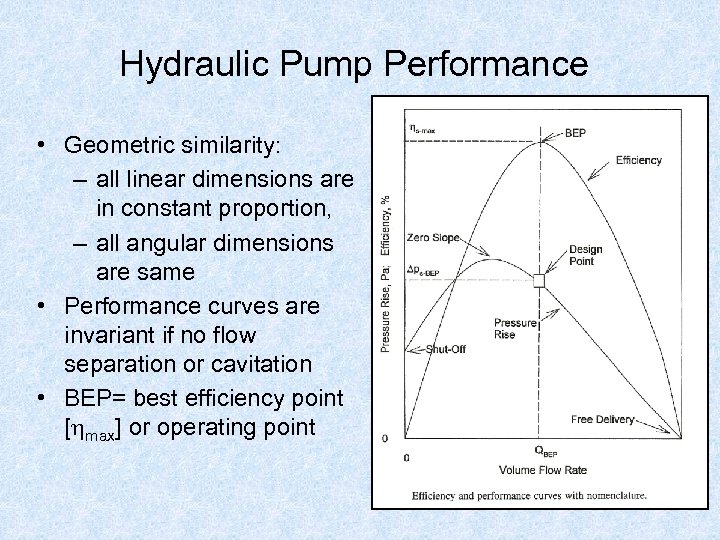
Hydraulic Pump Performance • Geometric similarity: – all linear dimensions are in constant proportion, – all angular dimensions are same • Performance curves are invariant if no flow separation or cavitation • BEP= best efficiency point [ max] or operating point

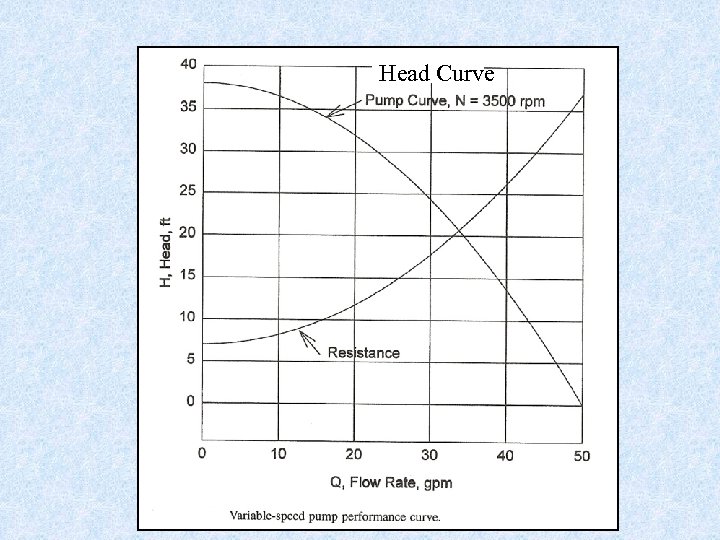
Head Curve

Example: Changing Level of Performance for a Given Design Pressure rise 27

Example: Changing Level of Performance for a Given Design Same fan but different size / speed 28

Scaling for Performance[limited by M, Re effects] 29

Example 30

Example 31

Define New Variable: Vary More Than One Parameter later 32

Similarity – Compressible Flow - Engine 33

Similarity – Compressible Flow 34

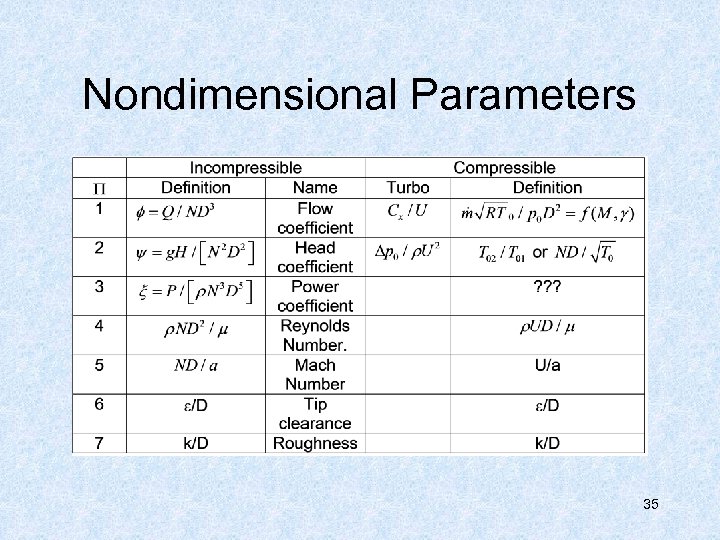
Nondimensional Parameters 35

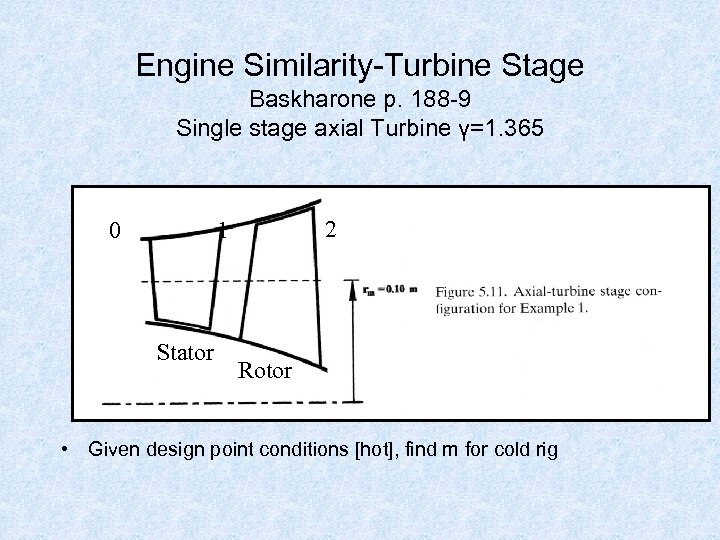
Engine Similarity-Turbine Stage Baskharone p. 188 -9 Single stage axial Turbine γ=1. 365 0 2 1 Stator Rotor • Given design point conditions [hot], find m for cold rig

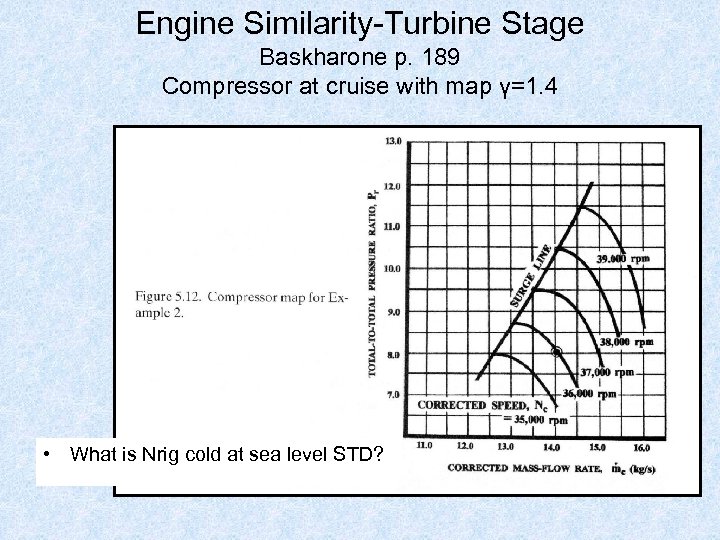
Engine Similarity-Turbine Stage Baskharone p. 189 Compressor at cruise with map γ=1. 4 • What is Nrig cold at sea level STD?

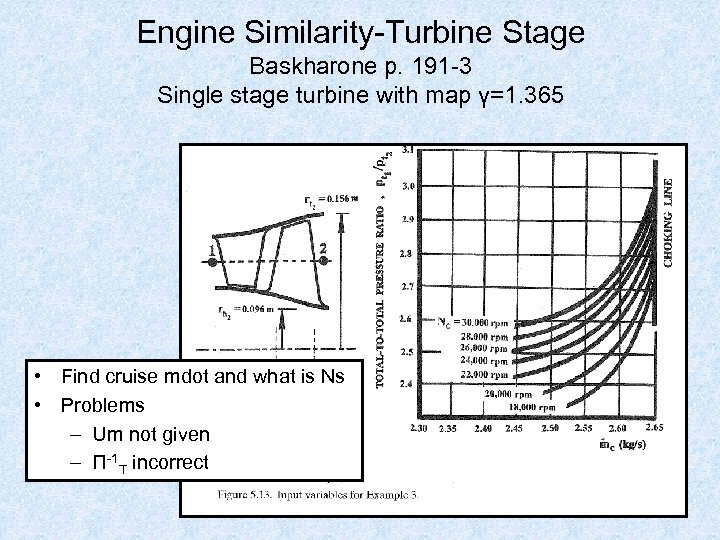
Engine Similarity-Turbine Stage Baskharone p. 191 -3 Single stage turbine with map γ=1. 365 • Find cruise mdot and what is Ns • Problems – Um not given – Π-1 T incorrect

Turbomachinery Lecture 4 a — Pi Theorem —