Tulip Mania Holland In 1623 a single

Tulip Mania: Holland • In 1623, a single bulb of a famous tulip variety could cost as much as a thousand Dutch florins (the average yearly income at the time was 150 florins). • A record was the sale of the most famous bulb, the Semper Augustus, for 6, 000 florins. • By 1636, tulips were traded on the stock exchanges of numerous Dutch towns and cities. • In February 1637 tulip traders could no longer get inflated prices for their bulbs, and they began to sell. The bubble burst. Panic developed. • Allegedly, thousands of Dutch, including businessmen and dignitaries, were financially ruined.

Stamps in Israel • November 1956, Itzik Friedman was a student at the Technion. He started trading stamps. Prices kept going up. • In March 1957, by buying and selling he had half-million pounds in cash. (could buy an apartment for 3000). • Father begged him to stop, but he wanted a million. • In May 1957, stamps fell to 50 percent of their nominal value • Itzik went tens of thousands of pounds in debt. • http: //www. haaretz. com/hasen/spages/1045743. html

Tea in China • Menghai is in a lush, mountainous tea-growing region in China. • Over the past decade, as the nation went wild for the region’s brand of tea, known as Pu’er, farmers bought minivans, manufacturers became millionaires and Chinese citizens plowed their savings into black bricks of compacted Pu’er. • From 1999 to 2007, the price of Pu’er, a fermented brew invented by Tang Dynasty traders, increased tenfold, to a high of $150 a pound for the finest aged Pu’er, before tumbling far below its preboom levels.

Bubbles and Crashes • Story of two people: Irving Fisher and Joseph Kennedy. • Irving Fisher – Famous economist and inventor. – He invented the Rolodex and made a small fortune from it (10 million in 1929). – Pretty much came up with the fundamental value of a stock. – Lost all his money in the 1929 crash. Said in 1929 “that prices have reached what looks like a permanently high plateau” – Yale had to buy his home and rent it back to him for free. Died in poverty.

Good timing • Joseph Kennedy – Made a fortune in the booming 20’s. – Decided to get out of the market when the boy shining his shoes gave him stock advice. – Father of JFK and Robert Kennedy.

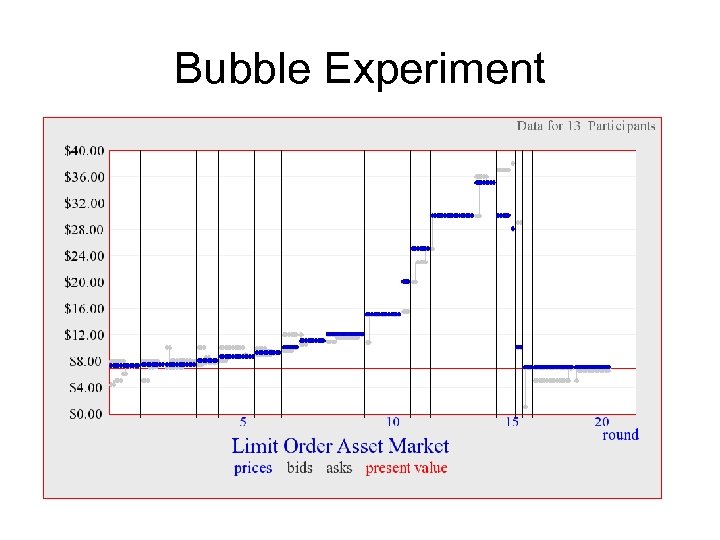
Bubble Experiment • • • Interest on cash was 10%. Dividend was 50% of $. 40 and 50% of $1. After 20 periods the price was $7. What should have been the price? Expected dividend was $. 7 An annuity that pays out. 7 with interest of. 1 is worth $7. • Thus, the PV is worth $7 at any time.

Bubble Experiment

Bubble Experiment • Why did you buy for above $7? • Why did anyone buy above (21 t)*. 7+7<$21? Above $27? • What strategies worked well? • What strategies didn’t?

Why are there bubbles? • Rational/near Rational. – p(t) is price at time t. d(t) is dividend at time t. r is interest. – p(t)=(E[p(t+1)]+E[d(t+1)])/(1+r) • Bubbles can grow rationally. – Say fundamental price is 0 w/o dividends. – Price can be 1 if there is a ½ chance of 0 and a ½ chance of price=2.

Why are there bubbles? • Information bubbles (cascade). – Prices normally convey information. – If markets don’t instantly aggregate information, then some information may come first. – If so, that information may count more than other. – Sometimes random noise can trick the market into reading the wrong signal. – Here people do not know there is a bubble.

Why are there bubbles? • Fads – Maybe investing in. coms made sense even if you didn’t think much. – Idea is that it makes sense to invest if you think others will. – Prices go up. – Keynes beauty contest. – French Impressionist paintings?

Bubble Experimental Research • VERNON L. SMITH, GERRY L. -SUCHANEK, AND ARLINGTON W. WILLIAMS 1988 – Had a random dividend. Not interest. – Should be a step function downward. – Found bubbles in both inexperienced and experienced subjects. • Dufwenberg, Lindqvist and Moore 2006 found that experience (and mixed experience) and small groups can kill a bubble. • Overall, most find no bubbles on the third time. • Hussam, Porter and Smith 2008 found that these bubbles can be rekindled with giving extra cash, lowering number of shares and increasing dividend. • Conclusion: bubbles do exist and are persistent.

Why bubbles? Irrationality • Perhaps the few irrational agents can drown out the rational agents. • If you think the fundamental price is 7 than you may not wish to buy above 7. You may have sold all your shares. • Allowing short-selling can fix this problem. • Haruvy and Noussair 2006 do that, but find while slightly reduced, bubbles persist.

Why Bubbles? Speculation. • VIVIAN LEI, CHARLES N. NOUSSAIR, AND CHARLES R. PLOTT 2001. • Perhaps everyone thinks there is a bigger sucker and buy in hopes of making a profit. Could be rational. • This paper prevents resale thus one can’t speculate. • Bubbles still persist.

Why bubbles? Common information. • David P. Porter and Vernon L. Smith 1995 add a futures market. • This should help share information about fundamentals tomorrow. • They find that this does make a difference, but does not eliminate bubbles completely.

Other. • Brokerage fees. Reduced bubbles. • Subject Pool: Executives, etc. No change. • Price change limits: No difference.

Homework question. • You are in an experimental asset market lasting 30 periods. Interest on cash each period is 20 percent. There is an asset that pays a risky dividend at the end of each period: a 50 percent chance it pays $. 40 and 50 percent chance it pays $1. 20. After 30 periods, the asset has a price of $4. (i) If the price trades at the fundamental value, what should the prices be each period. (i) extra hard What should the pattern of prices be if after 30 periods, the asset has a price of $5?