!Тема 2. Теорема Остроградского-Гаусса.ppt
- Количество слайдов: 60

Tuesday, February 6, 2018 Электростатика

Тема 2. ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА 2. 1. Силовые линии электростатического поля 2. 2. Поток вектора напряженности 2. 1. Силовые линии электростатического поля 2. 3. Теорема Остроградского-Гаусса 2. 2. Поток вектора напряженности 2. 4. Дифференциальная форма теоремы Остроградского. Гаусса 2. 3. Теорема Остроградского-Гаусса 2. 5. Вычисление электростатических полей с помощью 2. 4. Дифференциальная форма теоремы Остроградского - Гаусса Остроградского-Гаусса 2. 5. 1. Поле бесконечной однородно заряженнойполей с 2. 5. Вычисление электростатических плоскости помощью теоремы Остроградского-Гаусса 2. 5. 2. Поле двух равномерно заряженных плоскостей 2. 5. 1. Поле бесконечной однородно заряженной 2. 5. 3. Поле заряженного бесконечного цилиндра (нити) плоскости 2. 5. 4. Поле двух коаксиальных цилиндров с одинаковой 2. 5. 2. Поле двух равномерно заряженных линейной плотностью заряда, но разным знаком плоскостей 2. 5. 5. Поле заряженного пустотелого шара 2. 5. 3. Поле заряженного бесконечного цилиндра 2. 5. 6. Поле объемного заряженного шара (нити) 2. 5. 4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью заряда, но разным знаком 2. 5. 5. Поле заряженного пустотелого шара Tuesday, February 6, 2018 2. 5. 6. Поле объемного заряженного шара 2

2. 1. Силовые линии электростатического поля u Теорема Остроградского Гаусса, которую мы докажем и обсудим позже, устанавливает связь между электрическими зарядами и электрическим полем. Она представляет собой более общую и более изящную формулировку закона Кулона. Tuesday, February 6, 2018 3

u u u Tuesday, February 6, 2018 Остроградский Михаил Васильевич (1801 – 1862) отечественный математик и механик. Учился в Харьковском ун те (1816 – 1820), совершенствовал знания в Париже (1822 – 1827). Основные работы в области математического анализа, математической физики, теоретической механики. Решил ряд важных задач гидродинамики, теории теплоты, упругости, баллистики, электростатики, в частности задачу распространения волн на поверхности жидкости (1826 г. ). Получил дифференциальное уравнение распространения тепла в твердых телах и жидкостях. Известен теоремой Остроградского Гаусса в электро статике (1828 г. ). 4

u u u u Tuesday, February 6, 2018 Гаусс Карл Фридрих (1777 – 1855) немецкий математик, астроном и физик. Исследования посвящены многим разделам физики. В 1832 г. создал абсолютную систему мер (СГС), введя три основных единицы: единицу времени – 1 с, единицу длины – 1 мм, единицу массы – 1 мг. В 1833 г. совместно с В. Вебером построил первый в Германии электромагнитный телеграф. Еще в 1845 г. пришел к мысли о конечной скорости распростране ния электромагнитных взаимодействий. Изу чал земной магнетизм, изобрел в 1837 г. униполярный магнитометр, в 1838 г. – бифилярный. В 1829 г. Сформулировал принцип наименьшего принуждения (принцип Гаусса). Один из первых высказал в 1818 г. предположение о возможности существования неевклидовой геометрии. 5

u Основная ценность теоремы Остроградского Гаусса состоит в том, что она позволяет глубже понять природу электростатического поля и устанавливает более общую связь между зарядом и полем. Tuesday, February 6, 2018 6
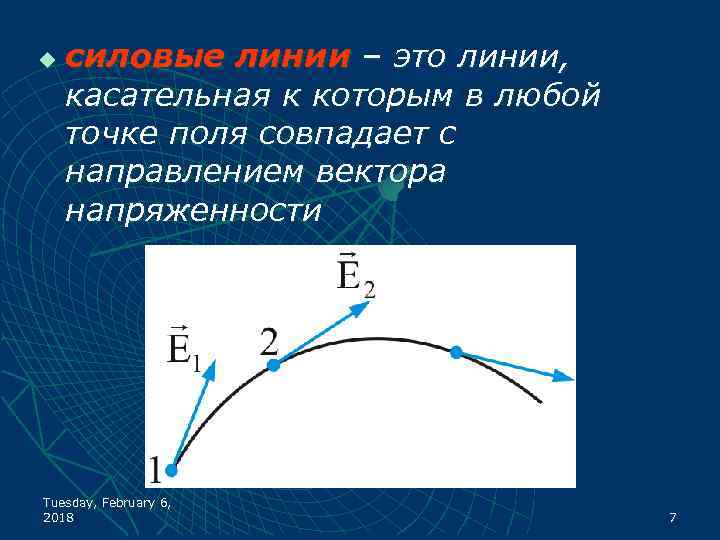
u силовые линии – это линии, касательная к которым в любой точке поля совпадает с направлением вектора напряженности Tuesday, February 6, 2018 7

u Однородным называется электростатическое поле, во всех точках которого напряженность одинакова по величине и направлению, т. е. Однородное электростатическое поле изображается параллельными силовыми линиями на равном расстоянии друг от друга Tuesday, February 6, 2018 8
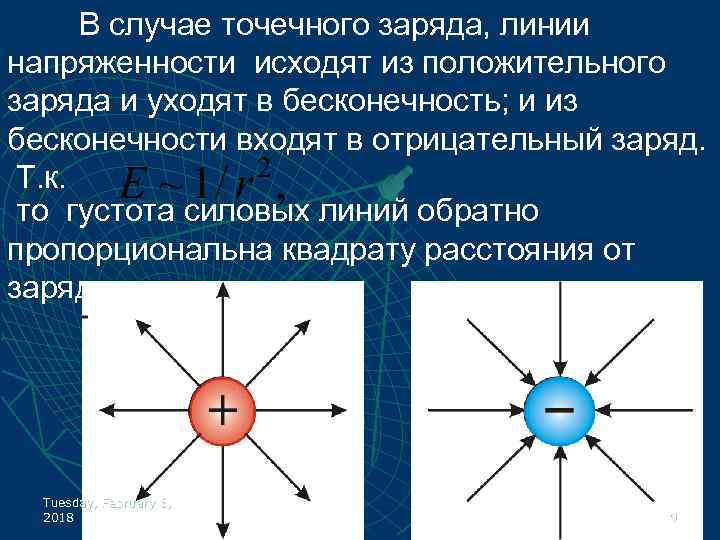
В случае точечного заряда, линии напряженности исходят из положительного заряда и уходят в бесконечность; и из бесконечности входят в отрицательный заряд. Т. к. то густота силовых линий обратно пропорциональна квадрату расстояния от заряда Tuesday, February 6, 2018 9
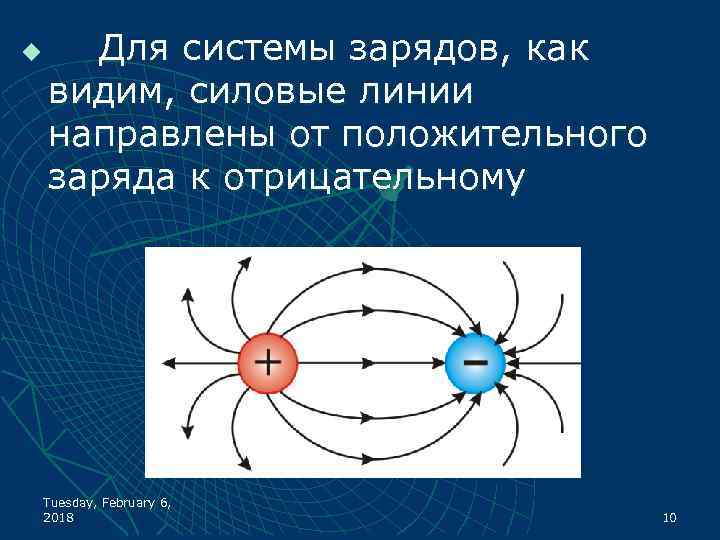
u Для системы зарядов, как видим, силовые линии направлены от положительного заряда к отрицательному Tuesday, February 6, 2018 10
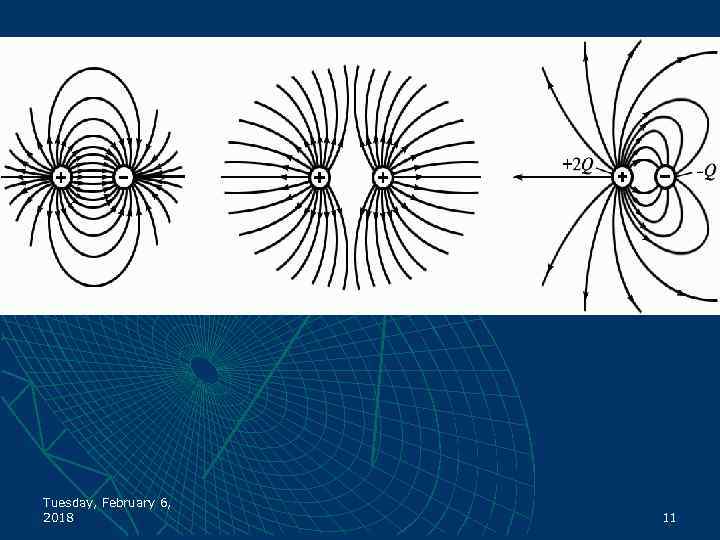
Tuesday, February 6, 2018 11

u Густота силовых линий должна быть такой, чтобы единичную площадку, нормальную к вектору напряженности пересекало такое их число, которое равно модулю вектора напряженности , т. е. Tuesday, February 6, 2018 12

u если на рисунке выделить площадку то напряженность изображенного поля будет равна Tuesday, February 6, 2018 13

2. 2. Поток вектора напряженности Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности Ф через эту поверхность u В векторной форме можно записать u – скалярное произведение двух векторов, где вектор. Tuesday, February 6, 2018 14

u Таким образом, поток вектора есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным. Tuesday, February 6, 2018 15

Для первого рисунка – поверхность А 1 окружает положительный заряд и поток здесь направлен наружу, т. е. Поверхность А 2 – окружает отрицательный заряд, здесь и направлен внутрь. Общий поток через поверхность А равен нулю. Tuesday, February 6, 2018 Опишите второй рисунок самостоятельно. 16

2. 3. Теорема Остроградского. Гаусса u Итак, по определению, поток вектора напряженности электрического поля равен числу линий напряженности, пересекающих поверхность S. Tuesday, February 6, 2018 17

u поток вектора напряженности через произвольную элементарную площадку d. S будет равен: Т. е. в однородном поле u В произвольном электрическом поле u Tuesday, February 6, 2018 18

u Подсчитаем поток вектора через произвольную замкнутую поверхность S, окружающую точечный заряд q. Окружим заряд q сферой S 1. Tuesday, February 6, 2018 19

Центр сферы совпадает с центром заряда. Радиус сферы S 1 равен R 1. u В каждой точке поверхности S 1 проекция Е на направление внешней нормали одинакова и равна u Tuesday, February 6, 2018 20
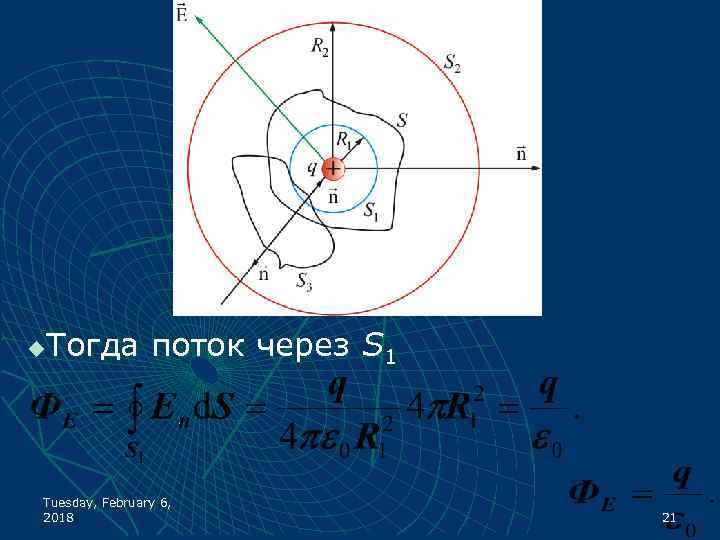
Тогда поток через S 1 u Tuesday, February 6, 2018 21
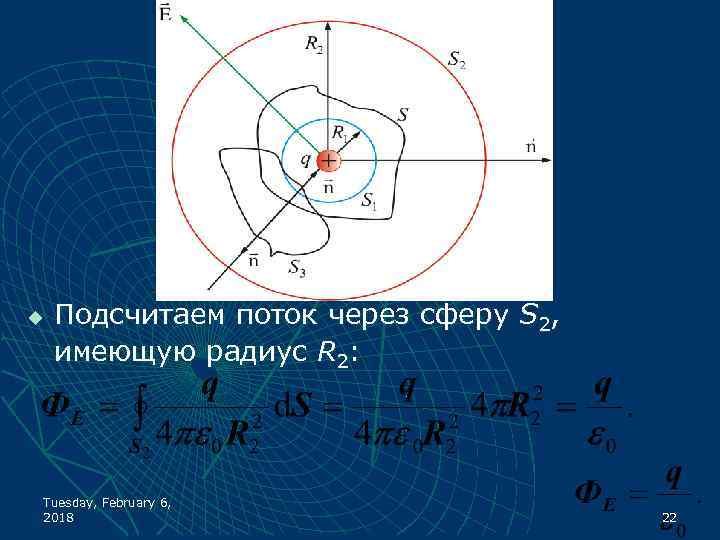
u Подсчитаем поток через сферу S 2, имеющую радиус R 2: Tuesday, February 6, 2018 22

u u Из непрерывности линии следует, что поток и через любую произвольную поверхность S будет равен этой же величине: Tuesday, February 6, 2018 – теорема Гаусса для одного заряда. 23

u u u Для любого числа произвольно расположенных зарядов, находящихся внутри поверхности: – теорема Гаусса для нескольких зарядов: Поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме всех зарядов, расположенных внутри поверхности, деленной на ε 0. Tuesday, February 6, 2018 24
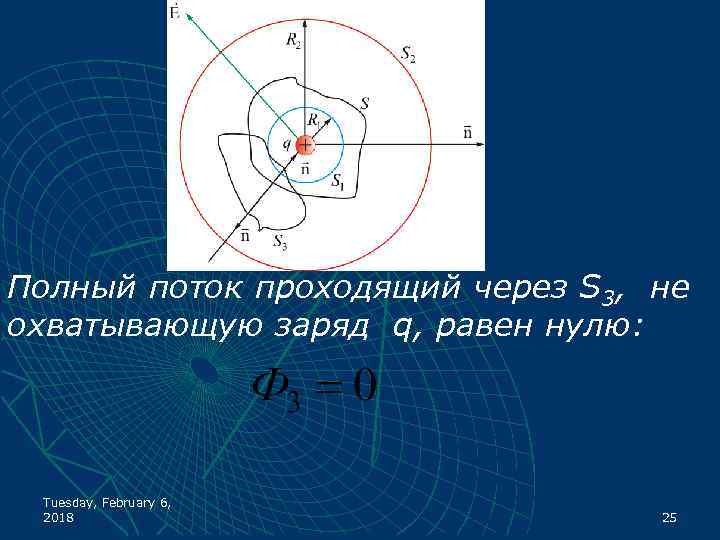
Полный поток проходящий через S 3, не охватывающую заряд q, равен нулю: Tuesday, February 6, 2018 25

u Таким образом, для точечного заряда q, полный поток через любую замкнутую поверхность S будет равен: – если заряд расположен внутри замкнутой поверхности; u – если заряд расположен вне замкнутой поверхности; u этот результат не зависит от формы поверхности, и знак потока совпадает со знаком заряда. u Tuesday, February 6, 2018 26

u u Электрические заряды могут быть «размазаны» с некоторой объемной плотностью различной в разных местах пространства: Здесь d. V – физически бесконечно малый объем, под которым следует понимать такой объем, который с одной стороны достаточно мал, чтобы в пределах его плотность заряда считать одинаковой, а с другой – достаточно велик, чтобы не могла проявиться дискретность заряда, т. е. то, что любой заряд кратен целому числу элементар ных Tuesday, February 6, зарядов электрона или протона. 2018 27

u Суммарный заряд объема d. V будет равен: u Тогда из теоремы Гаусса можно получить: u u – это ещё одна форма записи теоремы Остроградского-Гаусса, если заряд неравномерно распределен по объему. Tuesday, February 6, 2018 28

2. 4. Дифференциальная форма теоремы Остроградского-Гаусса u Пусть заряд распределен в пространстве V, с объемной плотностью. Тогда Tuesday, February 6, 2018 29

u u Теперь устремим , стягивая его к интересующей нас точке. Очевидно, что при этом будет стремиться к ρ в данной точке, т. е. Величину, являющуюся пределом отношения к V, при , называют дивергенцией поля Е Tuesday, February 6, 2018 30

u Дивергенция поля u Е. (2. 4. 1) Аналогично определяется дивергенция любого другого векторного поля. u Из этого определения следует, что дивергенция является скалярной функцией координат. u В декартовой системе координат u Tuesday, February 6, 2018 31

u Итак, (2. 4. 3) u Это теорема Остроградского. Гаусса в дифференциальной форме. u Написание многих формул упрощается, если ввести векторный дифференциальный оператор (Набла) u u где i, j, k – орты осей (единичные векторы). Tuesday, February 6, 2018 32

u u Сам по себе оператор смысла не имеет. Он приобретает смысл в сочетании с векторной или скалярной функцией, на которую символично умножается: дифференциальная форма теоремы Остроградского. Гаусса. Tuesday, February 6, 2018 33

В тех точках поля, где источники поля (положительные заряды), – u u u где – стоки (отрицательные заряды). Линии напряженности выходят из источников и заканчиваются в стоках. Tuesday, February 6, 2018 34
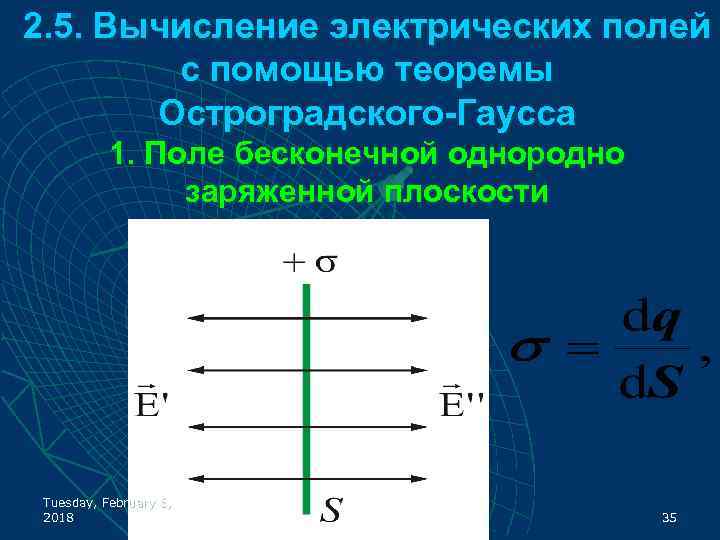
2. 5. Вычисление электрических полей с помощью теоремы Остроградского-Гаусса 1. Поле бесконечной однородно заряженной плоскости Tuesday, February 6, 2018 35
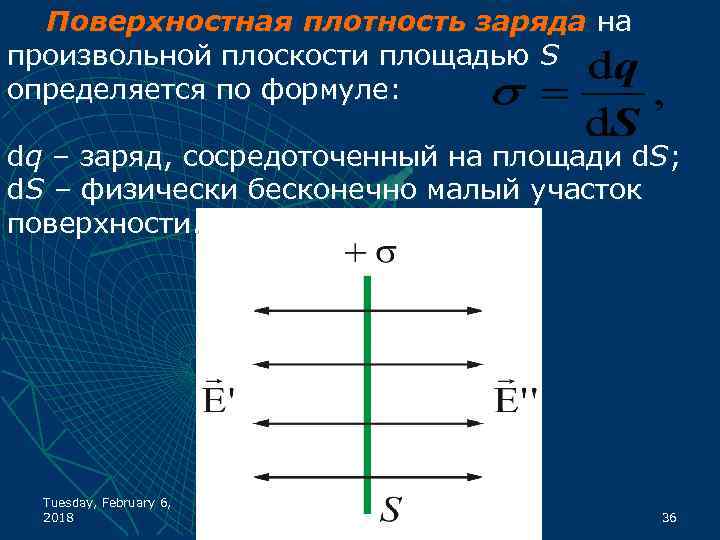
Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле: dq – заряд, сосредоточенный на площади d. S; d. S – физически бесконечно малый участок поверхности. Tuesday, February 6, 2018 36
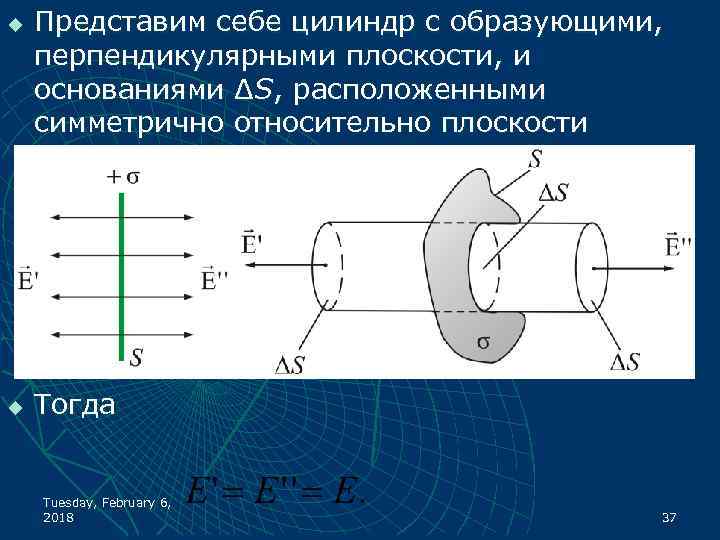
u u Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости Тогда Tuesday, February 6, 2018 37

u u Суммарный поток через замкнутую поверхность (цилиндр) будет равен: Внутри поверхности заключен заряд. Следовательно, из теоремы Остроградского Гаусса получим: откуда видно, что напряженность поля плоскости S : u (2. 5. 1) u Tuesday, February 6, 2018 38

2. 5. 2. Поле двух равномерно заряженных плоскостей u Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ Tuesday, February 6, 2018 39

u Результирующее поле, находится как суперпозиция полей, создаваемых каждой из плоскостей. Тогда внутри плоскостей u Вне плоскостей напряженность поля u Полученный результат справедлив и для плоскостей конечных размеров, если расстояние между плоскостями гораздо меньше линейных размеров плоскостей (плоский конденсатор). Tuesday, February 6, u 2018 40

• Распределение напряженности электростатического поля между пластинами конденсатора показано на рисунке: Tuesday, February 6, 2018 41

u u Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин): т. е. Механические силы, действующие между заряженными телами, называют пондермоторными. Tuesday, February 6, 2018 42

u Сила притяжения между пластинами конденсатора: u u где S – площадь обкладок конденсатора. Т. к. Это формула для расчета пондермоторной Tuesday, February 6, 2018 43 силы

2. 5. 3. Поле заряженного бесконечного цилиндра (нити) u Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью где dq – заряд, сосредоточенный на Tuesday, February 6, отрезке цилиндра 2018 u 44
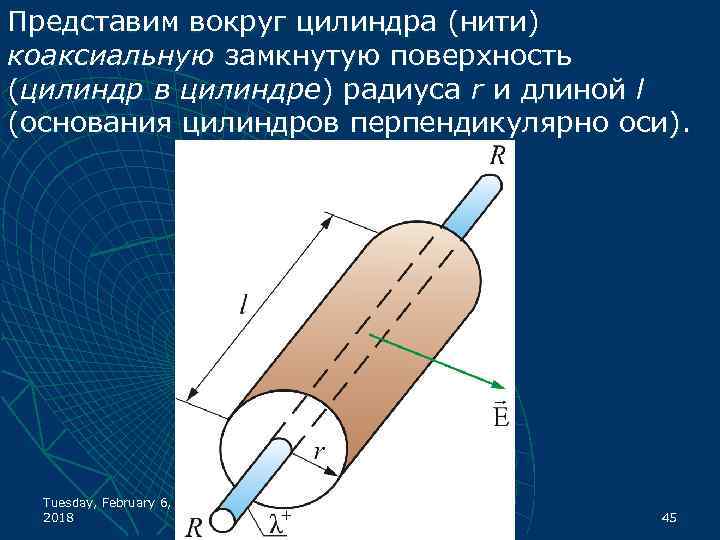
Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси). Tuesday, February 6, 2018 45

u u Для оснований цилиндров для боковой поверхности зависит от расстояния r. u т. е. Следовательно, поток вектора через рассматриваемую поверхность, равен Tuesday, February 6, 2018 46

u При u По теореме Остроградского Гаусса u Тогда u на поверхности будет заряд Если. February 6, , т. к. внутри Tuesday, 2018 замкнутой поверхности зарядов нет. 47
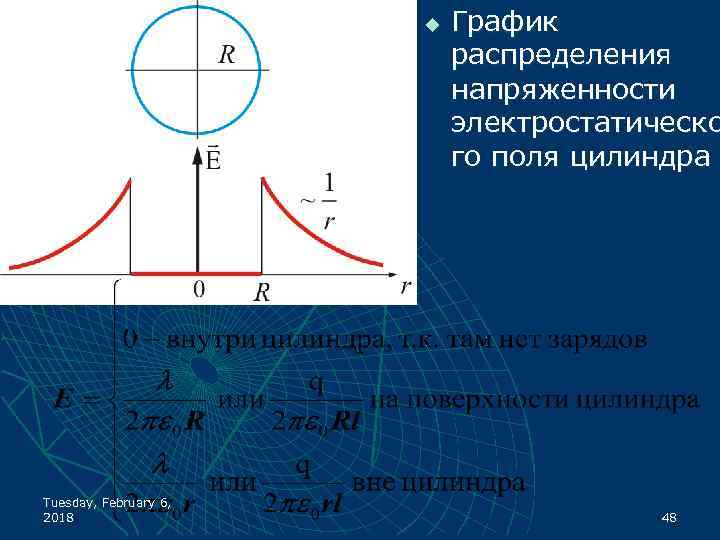
u Tuesday, February 6, 2018 График распределения напряженности электростатическо го поля цилиндра 48

2. 5. 4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком Tuesday, February 6, 2018 49
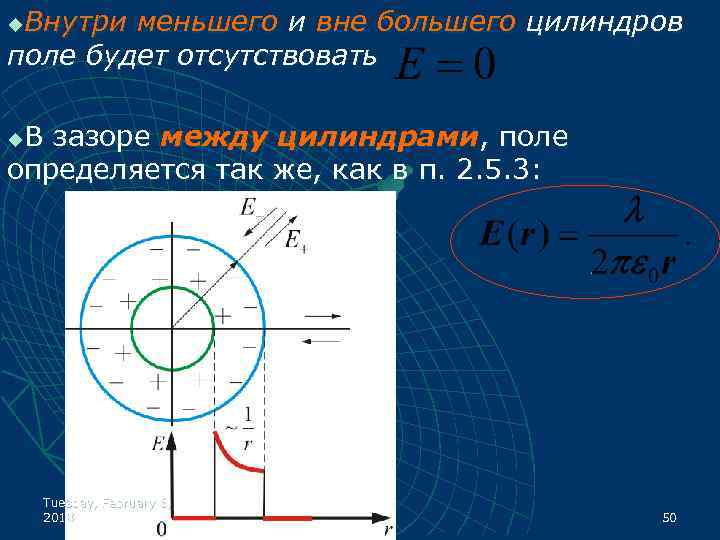
Внутри меньшего и вне большего цилиндров поле будет отсутствовать u В зазоре между цилиндрами, поле определяется так же, как в п. 2. 5. 3: u Tuesday, February 6, 2018 50

Таким образом для коаксиальных цилиндров имеем: u Tuesday, February 6, 2018 Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами намного меньше длины цилиндров (цилиндрический конденсатор). 51
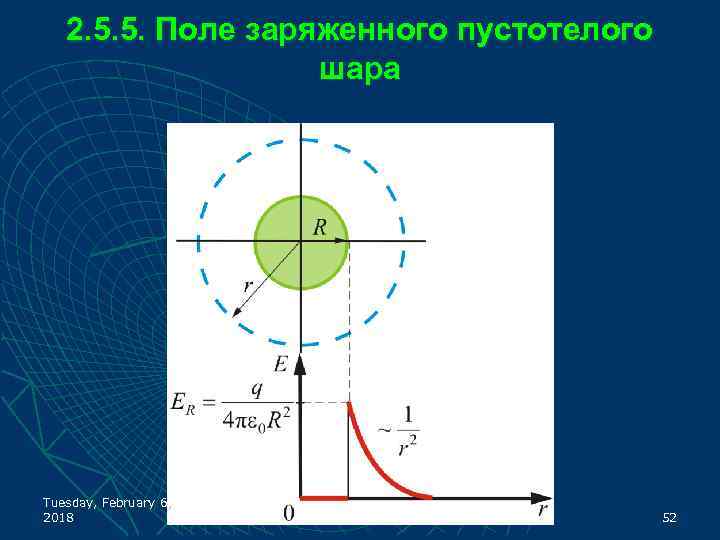
2. 5. 5. Поле заряженного пустотелого шара Tuesday, February 6, 2018 52
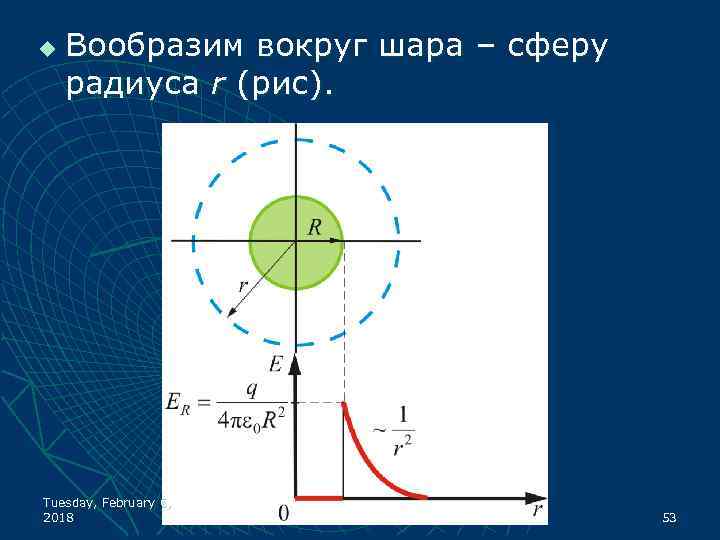
u Вообразим вокруг шара – сферу радиуса r (рис). Tuesday, February 6, 2018 53

u u u Если то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда откуда поле вне сферы: Внутри сферы, при поле будет равно нулю, т. к. там нет зарядов: Tuesday, February 6, 2018 54
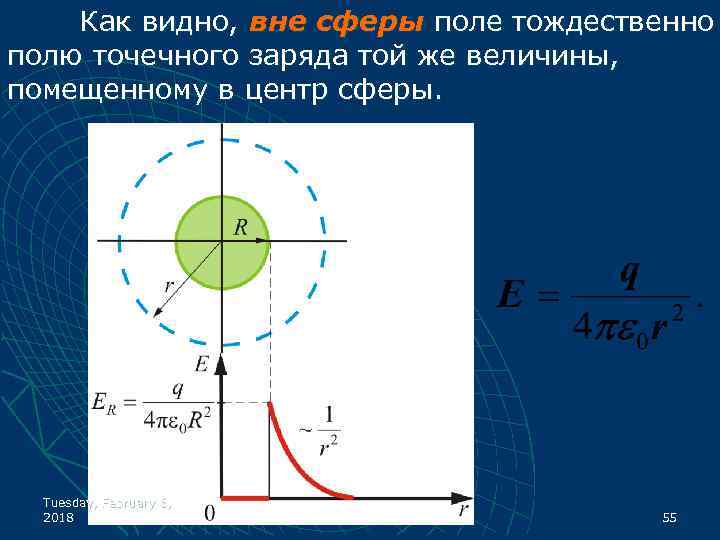
Как видно, вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы. Tuesday, February 6, 2018 55
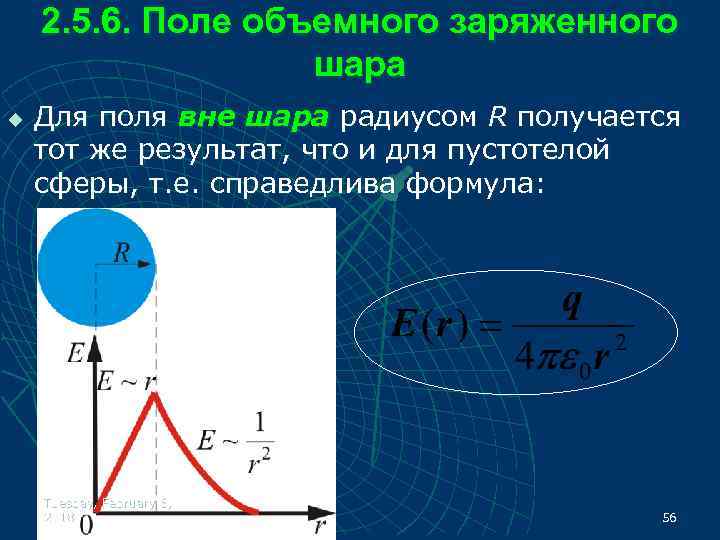
2. 5. 6. Поле объемного заряженного шара u Для поля вне шара радиусом R получается тот же результат, что и для пустотелой сферы, т. е. справедлива формула: Tuesday, February 6, 2018 56

u u Внутри шара при сферическая поверхность будет содержать в себе заряд, равный где ρ – объемная плотность заряда: объем шара: u u Тогда, по теореме Остроградского Гаусса: Tuesday, February 6, 2018 57
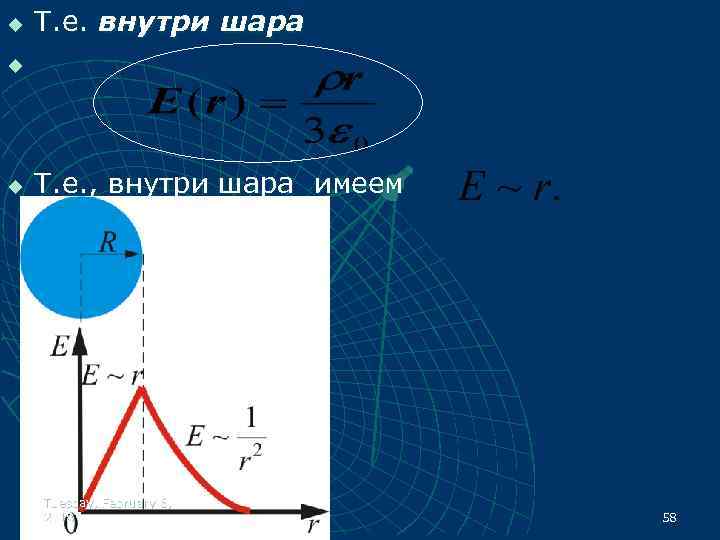
u Т. е. внутри шара u u Т. е. , внутри шара имеем Tuesday, February 6, 2018 58

Таким образом, имеем: поле объемного заряженного шара Tuesday, February 6, 2018 59

Tuesday, February 6, 2018 60
!Тема 2. Теорема Остроградского-Гаусса.ppt