TU e computational geometry introduction Mark de Berg

TU/e computational geometry introduction Mark de Berg

TU/e IPA Basic Course—Algorithms introduction • what is CG • applications randomized incremental construction • easy example: sorting • a general framework • applications to geometric problems and more …

TU/e Computational Geometry: Area within algorithms research dealing with spatial data (points, lines, polygons, circles, spheres, curves, … ) § design of efficient algorithms and data structures for spatial data focus on asymptotic running times of algorithms § elementary operations are assumed to take O(1) time and be available computing intersection point of two lines, distance between two points, etc

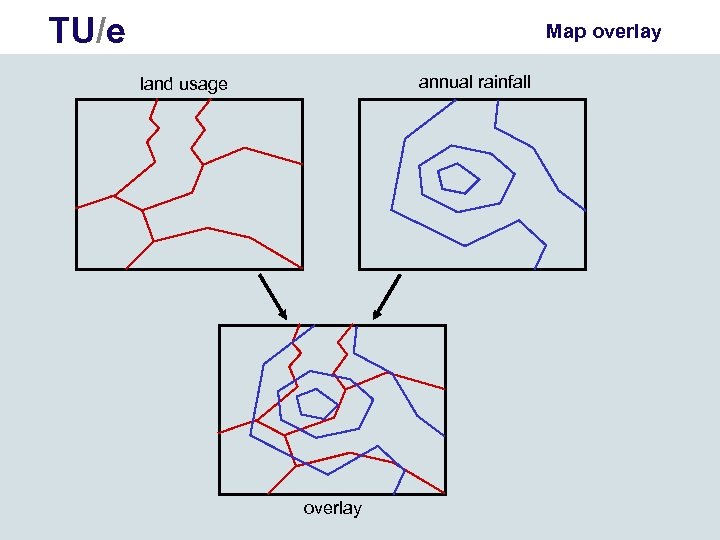
TU/e Map overlay annual rainfall land usage overlay

TU/e Computational Geometry example: compute all intersections in a set of line segments naïve algorithm for i = 1 to n for j =i+1 to n do if si intersects sj then report intersection Running time: O(n 2) Can we do better ?

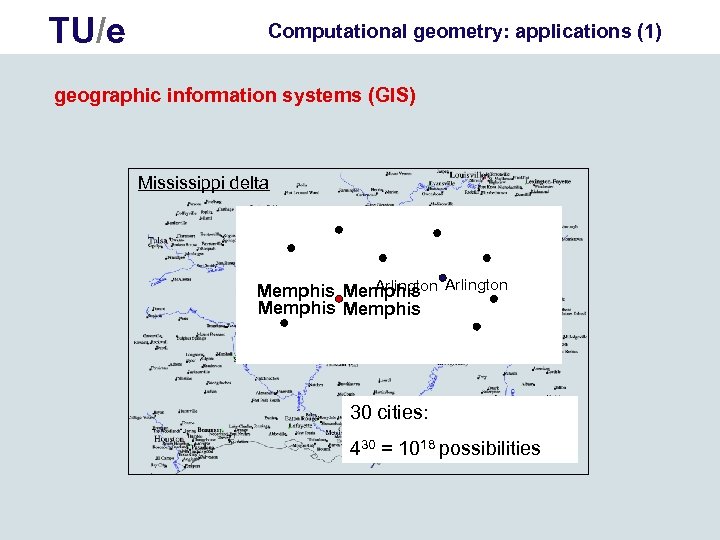
TU/e Computational geometry: applications (1) geographic information systems (GIS) Mississippi delta Arlington Memphis 30 cities: 430 = 1018 possibilities

TU/e Computational geometry: applications (2) computer-aided design and manufacturing (CAD/CAM) § motion planning § virtual walkthroughs 3 D model of power plant (12. 748. 510 triangles)

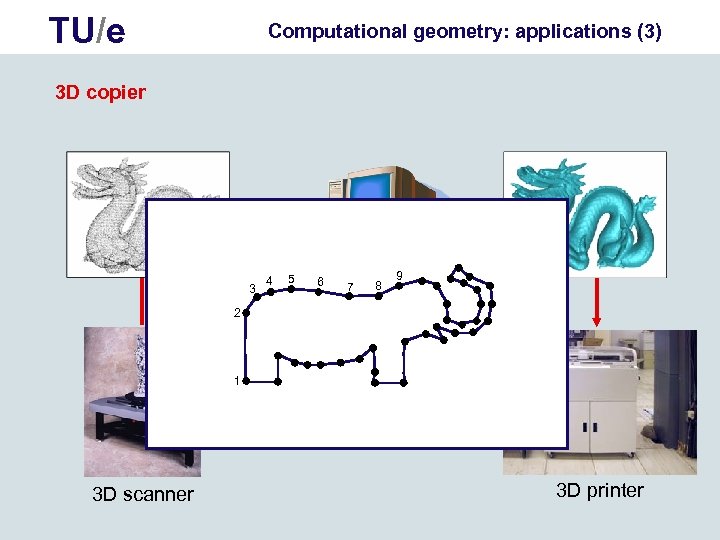
TU/e Computational geometry: applications (3) 3 D copier 3 9 5 6 surface reconstruction 8 7 4 2 1 3 D scanner 3 D printer

TU/e Computational geometry: applications (4) Other applications of surface reconstruction § digitizing cultural heritage § custom-fit products § reverse engineering

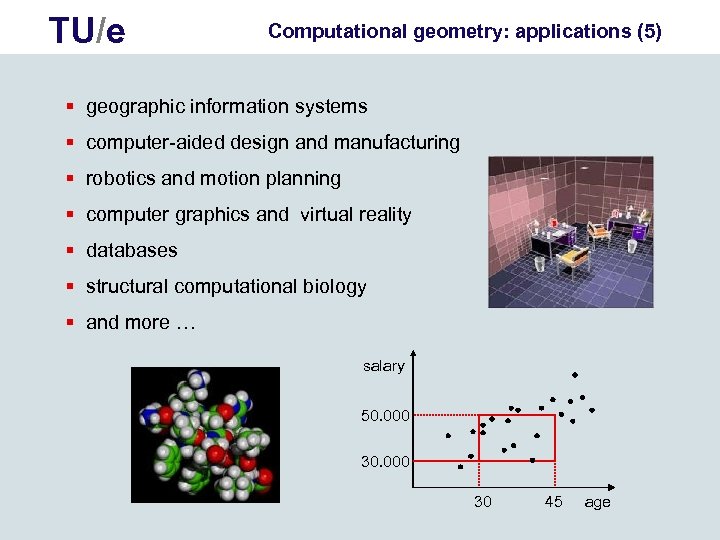
TU/e Computational geometry: applications (5) § geographic information systems § computer-aided design and manufacturing § robotics and motion planning § computer graphics and virtual reality § databases § structural computational biology § and more … salary 50. 000 30 45 age

TU/e Computational Geometry: algorithmic paradigms Deterministic algorithms § plane sweep § geometric divide-and-conquer Randomized algorithms § randomized incremental construction § random sampling today’s focus

TU/e EXERCISES 1. Let S be a set of n line segments in the plane. a) Design an algorithm that decides in O (n log n) time if there any intersections in S. Hint: Sort the endpoints on y-coordinates, and handle them in that order in a suitable manner. b) Extend the algorithm so that it reports all intersections in time O ((n+k) log n), where k is the number of intersections. For the experts: § Let u (n ) be the maximum number of pairs of points at distance 1 in a set of n points in the plane. Prove that u(n) = Ω (n log n). § Let D be a set of n discs in the plane. Prove that the union complexity of D is O (n ).

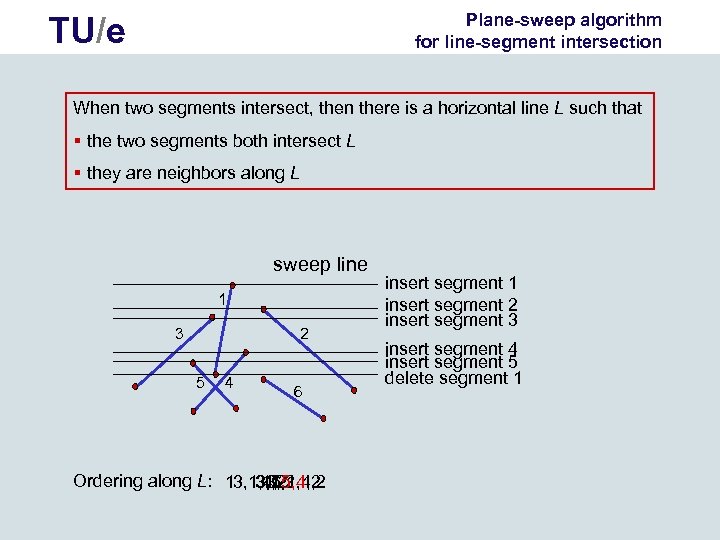
Plane-sweep algorithm for line-segment intersection TU/e When two segments intersect, then there is a horizontal line L such that § the two segments both intersect L § they are neighbors along L sweep line 1 3 2 5 4 6 Ordering along L: 13, 1, 4, 2 3, 1, 2 3, 5, 1, 4, 2 1, 2 3, 5, 4, 2 insert segment 1 insert segment 2 insert segment 3 insert segment 4 insert segment 5 delete segment 1

TU/e Plane sweep Segment. Intersect 1. Sort the endpoints by y-coordinate. Let p 1, …, p 2 n be the sorted set of endpoints. 2. Initialize empty search tree T. 3. for i = 1 to 2 n 4. do { if pi is the left endpoint of a segment s 5. then Insert s into the tree T 6. else Delete s from the tree T 7. Check all pairs of segments that become neighbors along the sweep line for intersection, report if there is an intersection. } Running time ? Extension to reporting all intersections ?

TU/e COFFEE

TU/e Lecture II: Randomized incremental construction Warm-up exercise: Analyze the worst-case and expected running time of the following algorithm. Paranoid. Max (A) (* A [1. . n ] is an array of n numbers *) 1. Randomly permute the elements in A 2. max : = A[1] 3. for i : = 2 to n 4. do if A [i ] > max 5. then { max : = A[i ] 6. for j = 1 to i -1 7. do if A[i ] > max then error } 8. return max

TU/e Worst-case running time Worst-case = O(1) + time for lines 2— 7 = O(1) + ∑ 2≤i≤n (time for i-th iteration) = O(1) + ∑ 2≤i≤n ∑ 1≤j≤i-1 O(1) = O(1) + ∑ 2≤i≤n O(i) = O(n 2)

TU/e Expected running time E [ looptijd ] = O(1) + E [ time for lines 2— 7 ] = O(1) + E [ ∑ 2≤i≤n (time for i-th iteration) ] = O(1) + ∑ 2≤i≤n E [ time for i-th iteration ] = O(1) + ∑ 2≤i≤n { Pr [ A[i] ≤ max { A[1. . i-1 ] } ] ∙ O(1) + Pr [ A[i] > max { A[1. . i-1 ] } ] ∙ O(i) } = O(1) + ∑ = O(n ) 2≤i≤n { 1 ∙ O(1) + (1/i ) ∙ O(i) }

TU/e EXERCISE 1. Give an algorithm that puts the elements of a given array A[1. . n] into random order. Your algorithm should be such that every possible permutation is equally likely to be the result.

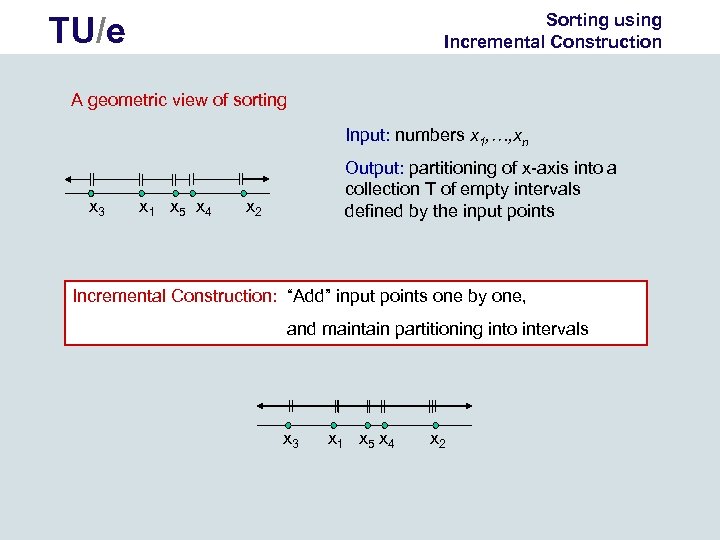
Sorting using Incremental Construction TU/e A geometric view of sorting Input: numbers x 1, …, xn x 3 x 1 x 5 x 4 Output: partitioning of x-axis into a collection T of empty intervals defined by the input points x 2 Incremental Construction: “Add” input points one by one, and maintain partitioning into intervals x 3 x 1 x 5 x 4 x 2

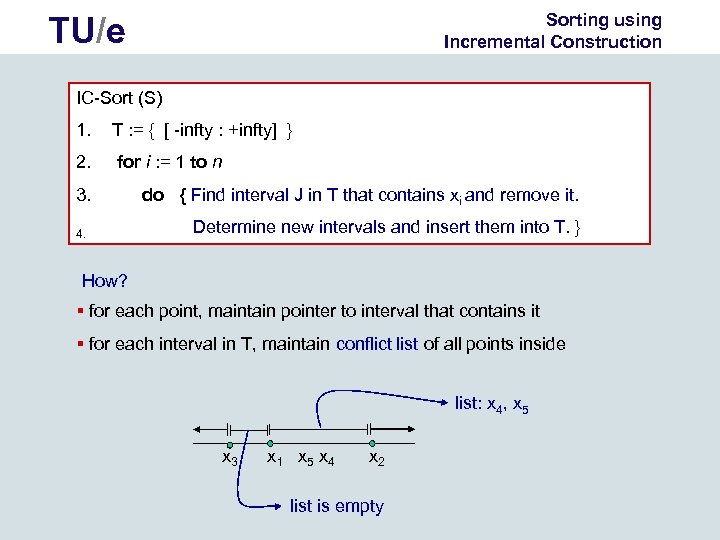
Sorting using Incremental Construction TU/e IC-Sort (S) 1. T : = { [ -infty : +infty] } 2. for i : = 1 to n 3. 4. do { Find interval J in T that contains xi and remove it. Determine new intervals and insert them into T. } How? § for each point, maintain pointer to interval that contains it § for each interval in T, maintain conflict list of all points inside list: x 4, x 5 x 3 x 1 x 5 x 4 x 2 list is empty

Sorting using Incremental Construction TU/e IC-Sort (S) 1. T : = { [ -infty : +infty] } 2. for i : = 1 to n 3. do { Find interval J in T that contains xi and remove it. 4. Determine new empty intervals and insert them into T. 5. Split conflict list of J to get the two new conflict lists. } § for each point, maintain pointer to interval that contains it § for each interval in T, maintain conflict list of all points inside Time analysis: TOTAL TIME: O ( total size of conflict lists of all intervals that ever appear) WORST-CASE: O(n 2)

Sorting using Incremental Construction TU/e RIC-Sort (S) 1. Randomly permute input points 2. T : = { [ -infty : +infty] } 3. for i : = 1 to n 4. do { Find interval J in T that contains xi and remove it. 5. Determine new empty intervals and insert them into T. 6. Split conflict list of J to get the two new conflict lists. } § for each point, maintain pointer to interval that contains it § for each interval in T, maintain conflict list of all points inside Time analysis: TOTAL TIME: O ( total size of conflict lists of all intervals that are created) EXPECTED TIME: ? ?

TU/e An abstract framework for RIC S = set of n (geometric) objects; the input D: assigns a defining set D(Δ) ∩ K: assigns a killing set K(Δ) ∩ C = set of configurations S to every configuration Δ є C D(Δ) ∩ configuration Δ є C is active over a subset S’ S’ ∩ 4 -tuple (S, C, D, K) is called a configuration space S if: and K(Δ) ∩ S’ = o / T(S) = active configurations over S; the output

Sorting using Incremental Construction TU/e RIC(S) 1. Compute random permutation x 1, …xn of input elements 2. T : = { active configurations over empty set } 3. for i : = 1 to n 4. do { Remove all configurations Δ with xi є K(Δ) from T. 5. Determine new active configurations; insert them into T. 6. Construct conflict lists of new active configurations. } § for each xi, maintain pointers to all configurations Δ such that xi є K(Δ) § for each configuration Δ in T, maintain conflict list of all xi є K(Δ) Theorem: Expected total size of conflict lists of all created configs: O( ∑ 1≤i≤n (n / i 2) ∙ E [ # active configurations in step i ] )

TU/e EXERCISE 1. Use theorem to prove that the running time of the RIC algorithm for sorting runs in O( n log n ) time.

TU/e LUNCH

TU/e Lecture III RIC: more applications Voronoi diagrams and Delaunay triangulations

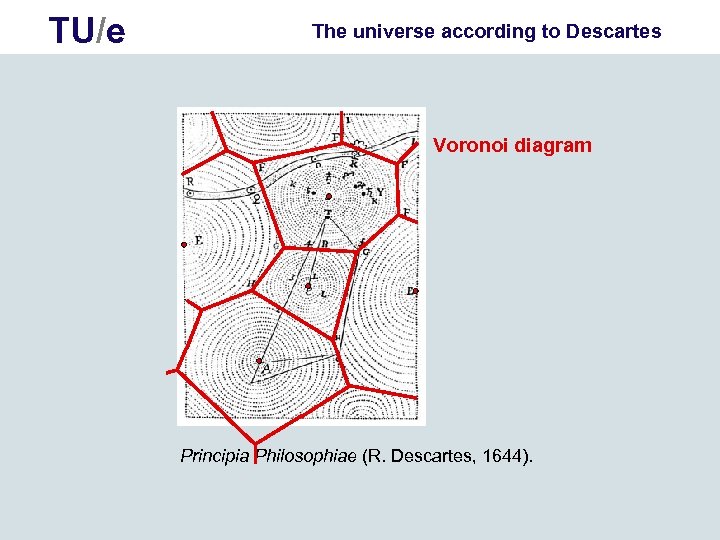
TU/e The universe according to Descartes Voronoi diagram Principia Philosophiae (R. Descartes, 1644).

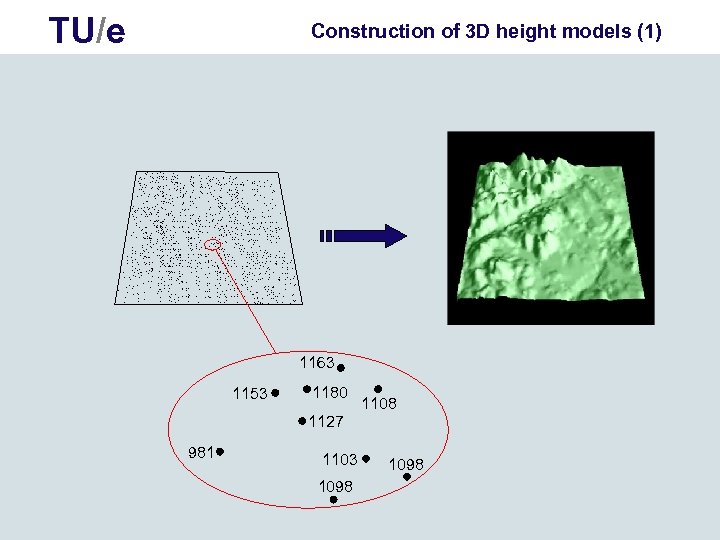
TU/e Construction of 3 D height models (1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1163 1153 1180 1108 1127 981 1103 1098

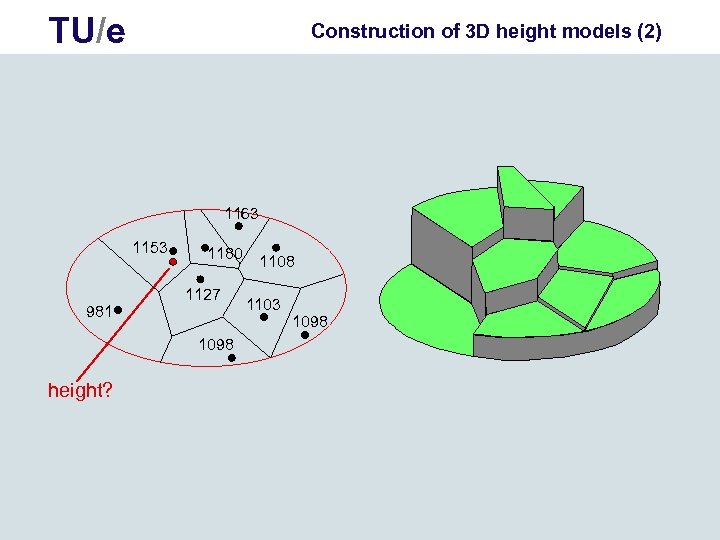
TU/e Construction of 3 D height models (2) 1163 1153 981 1180 1127 1098 height? 1108 1103 1098

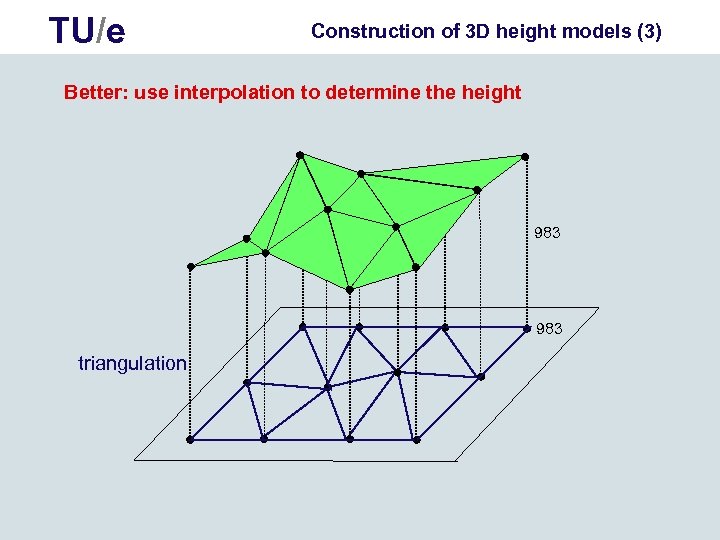
TU/e Construction of 3 D height models (3) Better: use interpolation to determine the height 983 triangulation

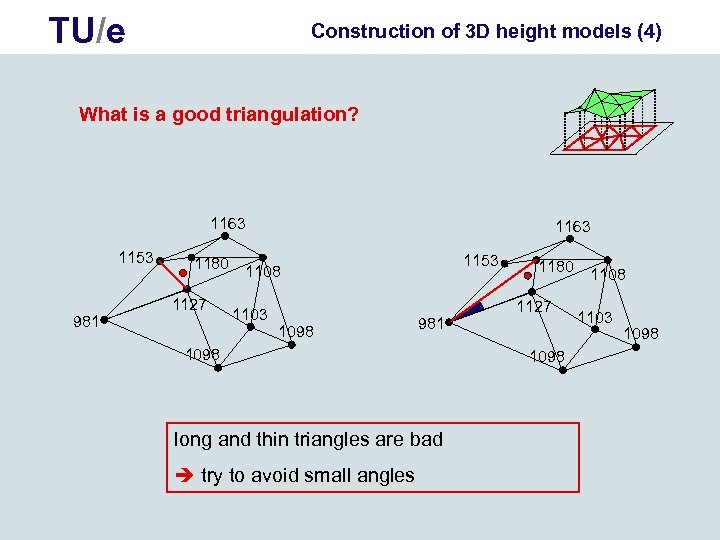
TU/e Construction of 3 D height models (4) What is a good triangulation? 1163 1153 981 1180 1127 1163 1153 1108 1103 1098 981 1098 long and thin triangles are bad try to avoid small angles 1180 1127 1098 1103 1098

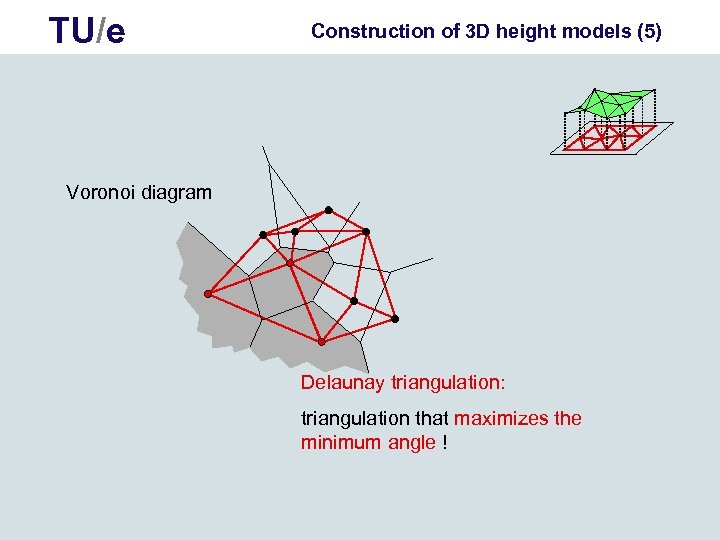
TU/e Construction of 3 D height models (5) Voronoi diagram Delaunay triangulation: triangulation that maximizes the minimum angle !

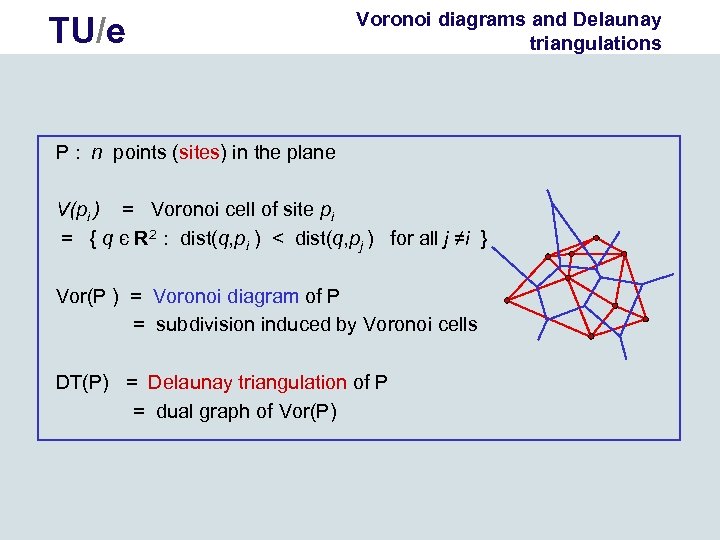
TU/e Voronoi diagrams and Delaunay triangulations P : n points (sites) in the plane V(pi ) = Voronoi cell of site pi = { q є R 2 : dist(q, pi ) < dist(q, pj ) for all j ≠i } Vor(P ) = Voronoi diagram of P = subdivision induced by Voronoi cells DT(P) = Delaunay triangulation of P = dual graph of Vor(P)

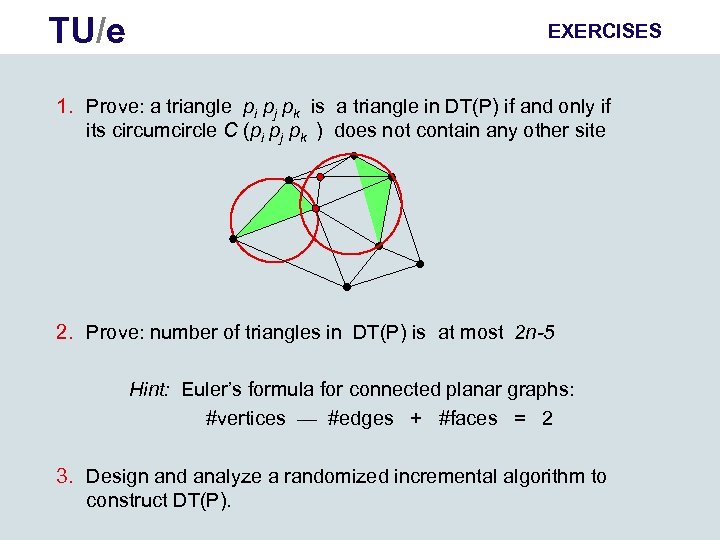
TU/e EXERCISES 1. Prove: a triangle pi pj pk is a triangle in DT(P) if and only if its circumcircle C (pi pj pk ) does not contain any other site 2. Prove: number of triangles in DT(P) is at most 2 n-5 Hint: Euler’s formula for connected planar graphs: #vertices — #edges + #faces = 2 3. Design and analyze a randomized incremental algorithm to construct DT(P).

TU/e COFFEE

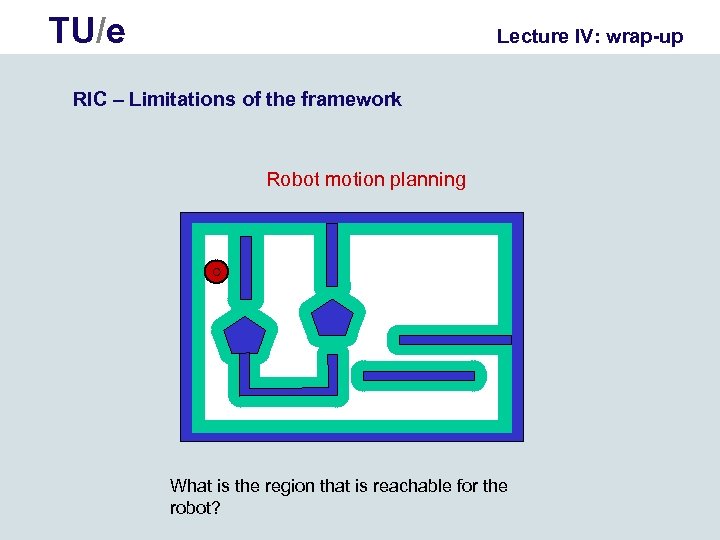
TU/e Lecture IV: wrap-up RIC – Limitations of the framework Robot motion planning What is the region that is reachable for the robot?

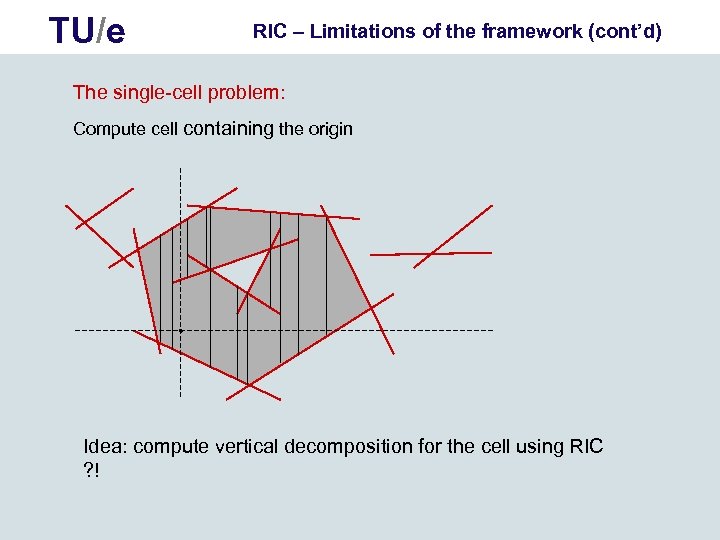
TU/e RIC – Limitations of the framework (cont’d) The single-cell problem: Compute cell containing the origin Idea: compute vertical decomposition for the cell using RIC ? !

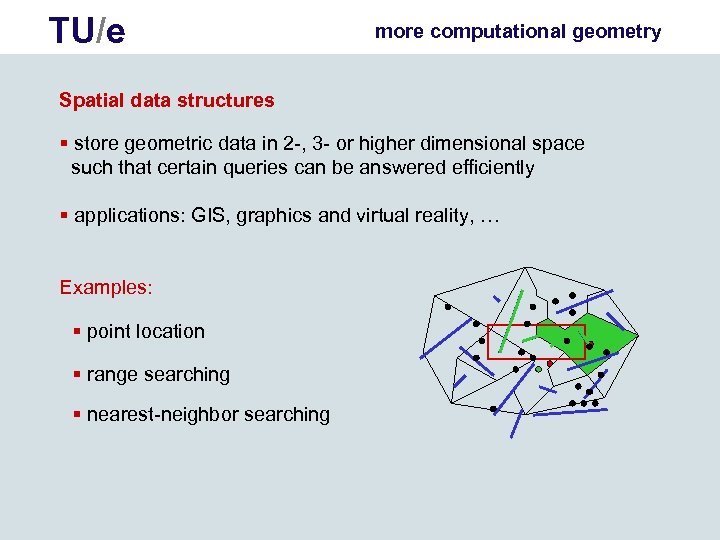
TU/e more computational geometry Spatial data structures § store geometric data in 2 -, 3 - or higher dimensional space such that certain queries can be answered efficiently § applications: GIS, graphics and virtual reality, … Examples: § point location § range searching § nearest-neighbor searching

TU/e and more … § plane sweep § parametric search § arrangements § geometric duality, inversion, Plücker coordinates, … § kinetic data structures § core sets § Davenport-Schinzel sequences §…