Trigonometry Pythagoras Theorem Trigo Ratios of Acute

Trigonometry Pythagoras Theorem & Trigo Ratios of Acute Angles

Pythagoras Theorem a 2 + b 2 = c 2 where c is the hypotenuse while a and b are the lengths of the other two sides. c a b

Trigo Ratios of Acute angles P hypotenuse opposite O adjacent Q Hypotenuse = side opposite right angle/longest side Adjacent = side touching theta Opposite= side opposite theta

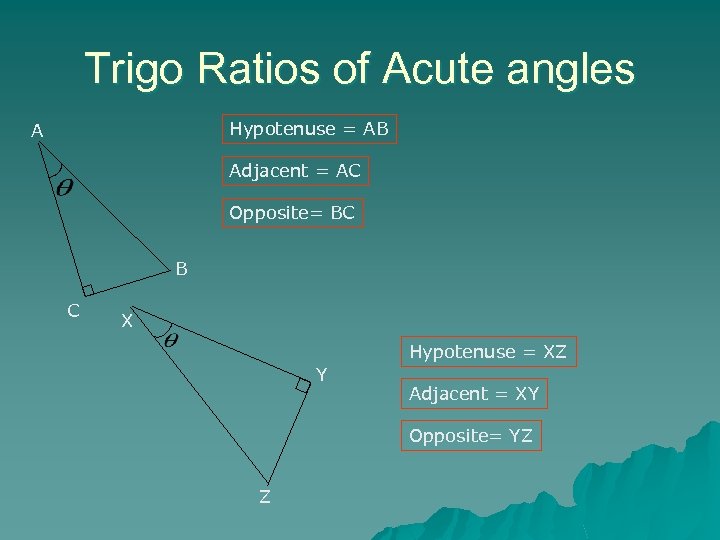Trigo Ratios of Acute angles Hypotenuse = AB A Adjacent = AC Opposite= BC B C X Hypotenuse = XZ Y Adjacent = XY Opposite= YZ Z

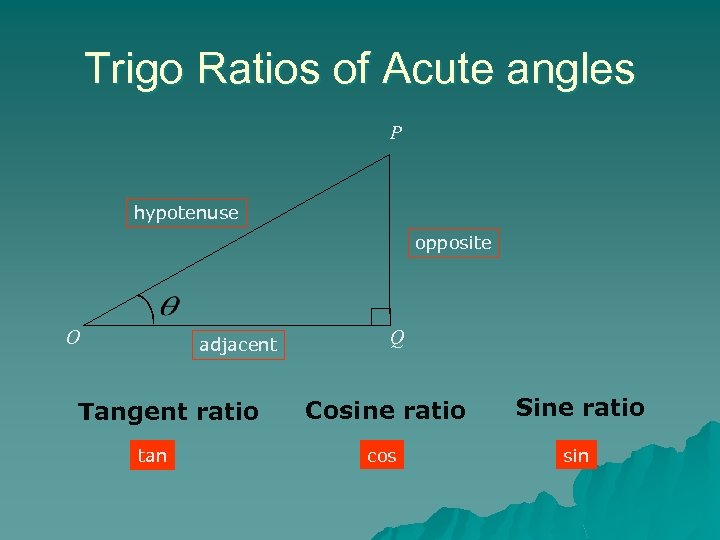Trigo Ratios of Acute angles P hypotenuse opposite O adjacent Tangent ratio tan Q Cosine ratio Sine ratio cos sin

Trigo Ratios of Acute angles P hypotenuse opposite O adjacent Q

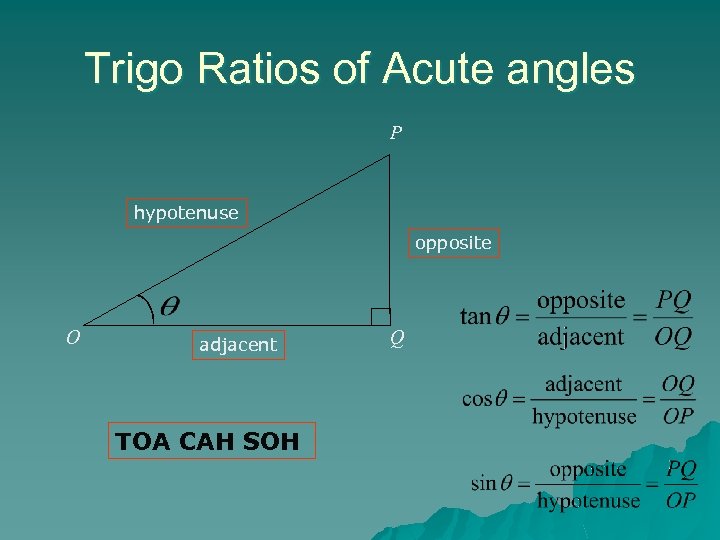Trigo Ratios of Acute angles P hypotenuse opposite O adjacent TOA CAH SOH Q

Exercise 1 13 5 12 5 3 4

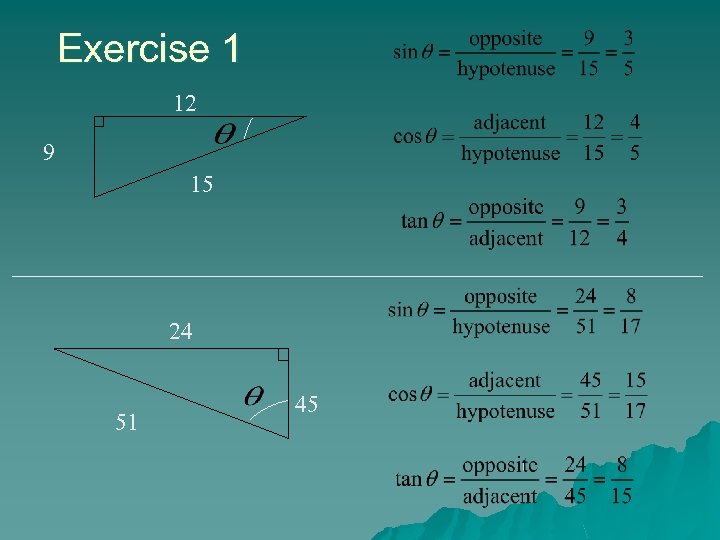Exercise 1 12 9 15 24 51 45

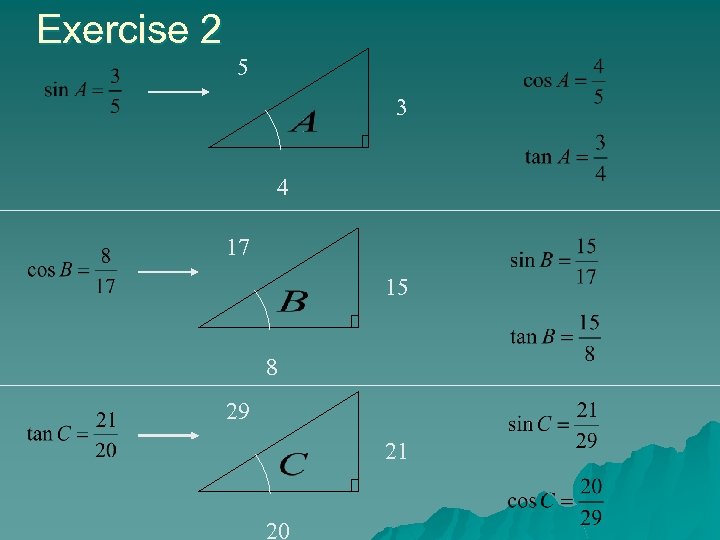Exercise 2 5 3 4 17 15 8 29 21 20

Exercise 3

Exercise 4 sin (30° 2) = 0. 2588… sin ( 2) = sin 2 cos 2 = 2 cos sin 30° 2 = 0. 25 cos (2× 30°) = 0. 5 2× cos 30° = 1. 732… tan (A + B) = tan A + tan B tan (10° + 30°) = 0. 839… tan 10° + tan 30° = 0. 753

Exercise 5 sin = 0. 4537 = sin-1 0. 4537 = 26. 981≈27. 0° cos = 0. 3625 = cos-1 0. 3625 = 68. 746≈68. 7° tan = 4. 393 = tan-1 4. 393 = 77. 176≈77. 2°

Exercise 5 sin = 0. 8888 = sin-1 0. 8888 = 62. 722≈62. 7° cos = 0. 9999 = cos-1 0. 9999 = 0. 8102≈0. 8° tan = 0. 5177 = tan-1 0. 5177 = 27. 370≈27. 4°

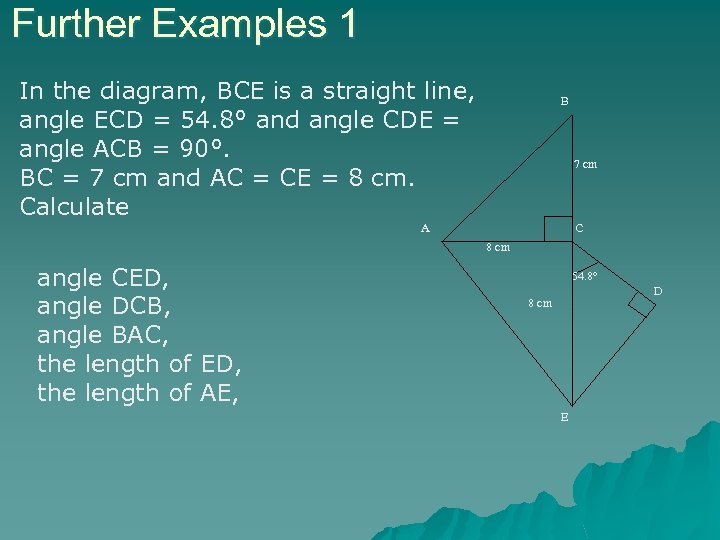Further Examples 1 In the diagram, BCE is a straight line, angle ECD = 54. 8° and angle CDE = angle ACB = 90°. BC = 7 cm and AC = CE = 8 cm. Calculate B 7 cm A C 8 cm angle CED, angle DCB, angle BAC, the length of ED, the length of AE, 54. 8° D 8 cm E

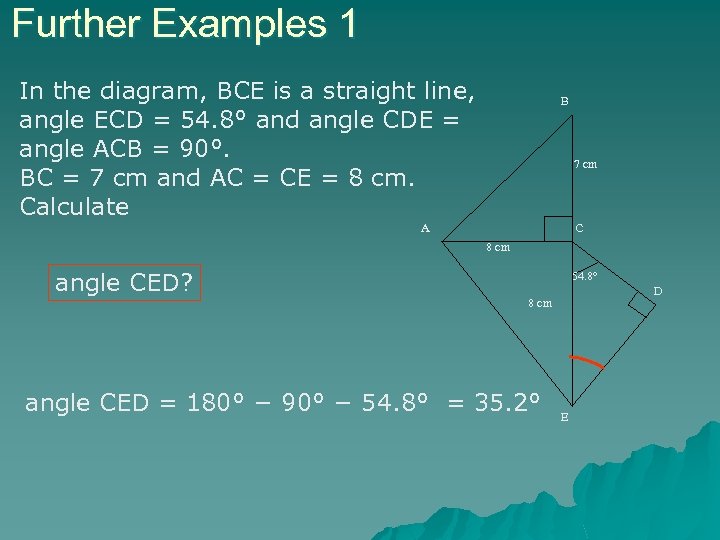Further Examples 1 In the diagram, BCE is a straight line, angle ECD = 54. 8° and angle CDE = angle ACB = 90°. BC = 7 cm and AC = CE = 8 cm. Calculate B 7 cm A C 8 cm angle CED? 54. 8° D 8 cm angle CED = 180° − 90° − 54. 8° = 35. 2° E

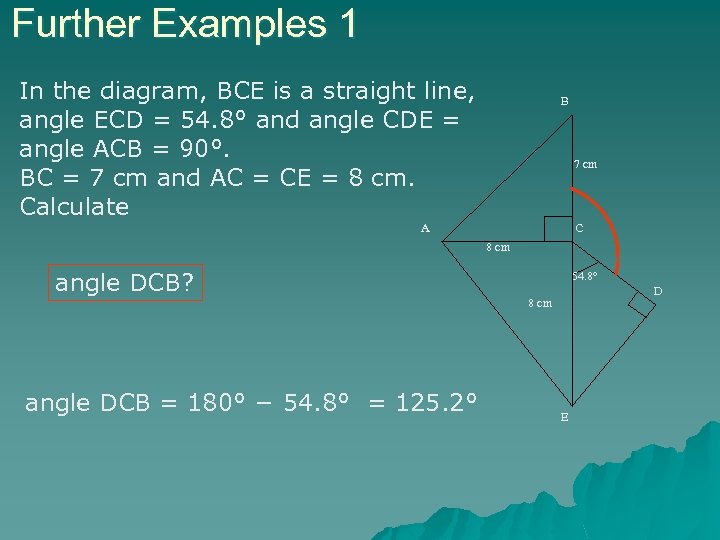Further Examples 1 In the diagram, BCE is a straight line, angle ECD = 54. 8° and angle CDE = angle ACB = 90°. BC = 7 cm and AC = CE = 8 cm. Calculate B 7 cm A C 8 cm angle DCB? 54. 8° D 8 cm angle DCB = 180° − 54. 8° = 125. 2° E

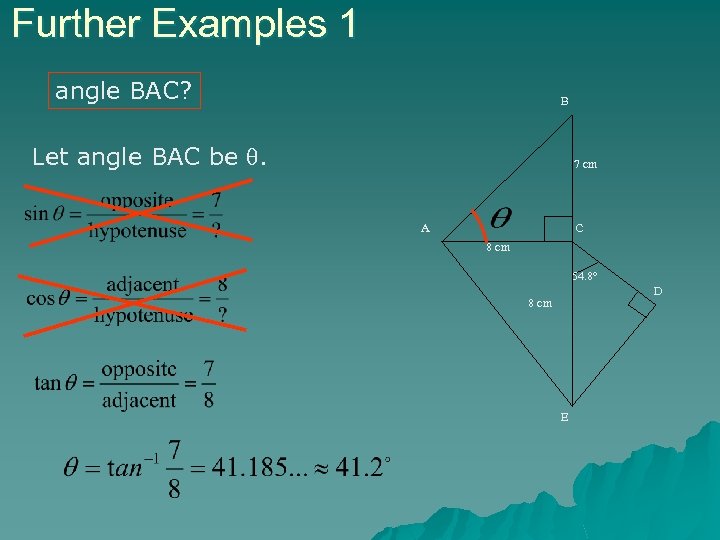Further Examples 1 angle BAC? B Let angle BAC be . 7 cm A C 8 cm 54. 8° D 8 cm E

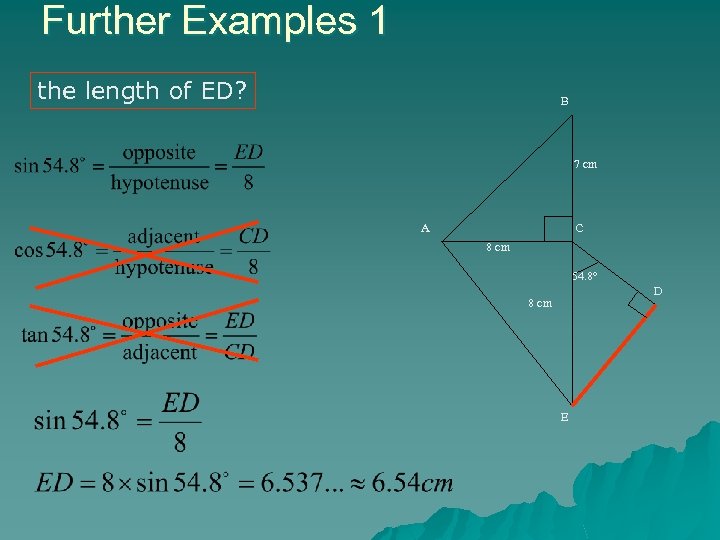Further Examples 1 the length of ED? B 7 cm A C 8 cm 54. 8° D 8 cm E

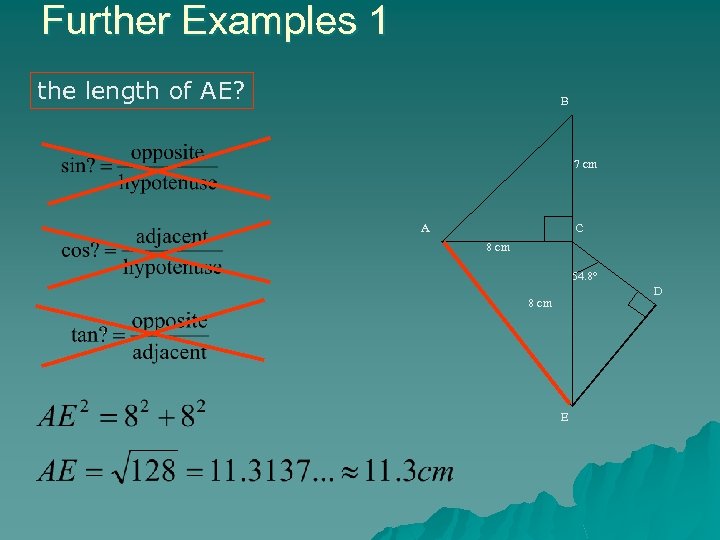Further Examples 1 the length of AE? B 7 cm A C 8 cm 54. 8° D 8 cm E

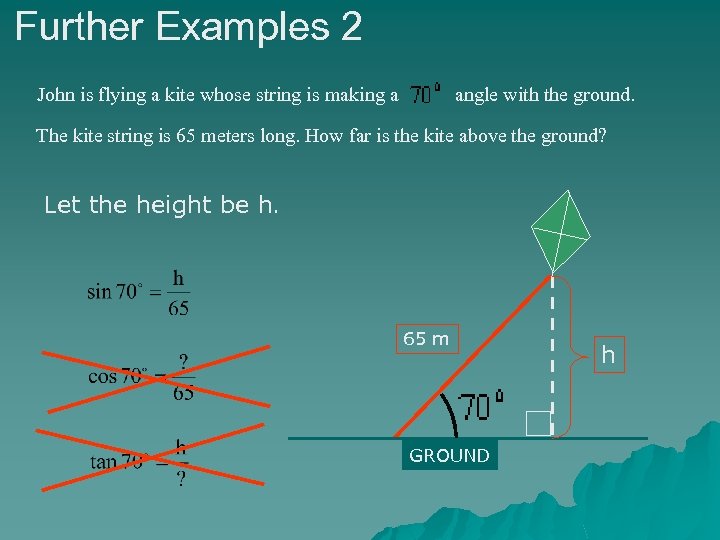Further Examples 2 John is flying a kite whose string is making a angle with the ground. The kite string is 65 meters long. How far is the kite above the ground? Let the height be h. 65 m GROUND h

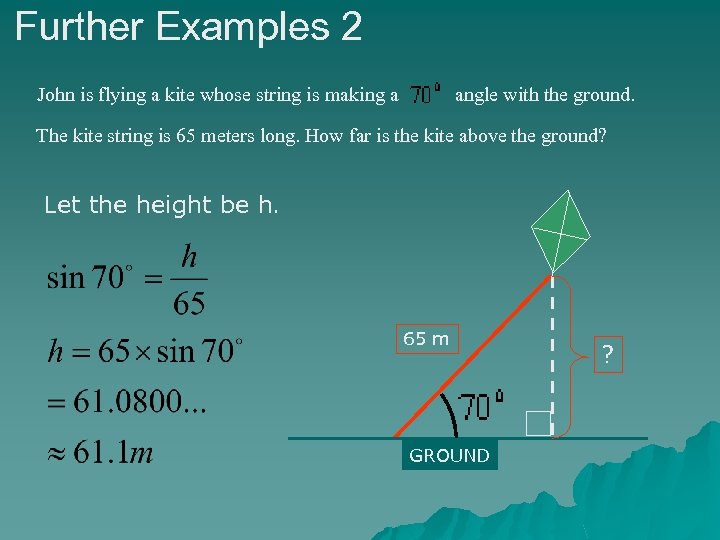Further Examples 2 John is flying a kite whose string is making a angle with the ground. The kite string is 65 meters long. How far is the kite above the ground? Let the height be h. 65 m GROUND ?

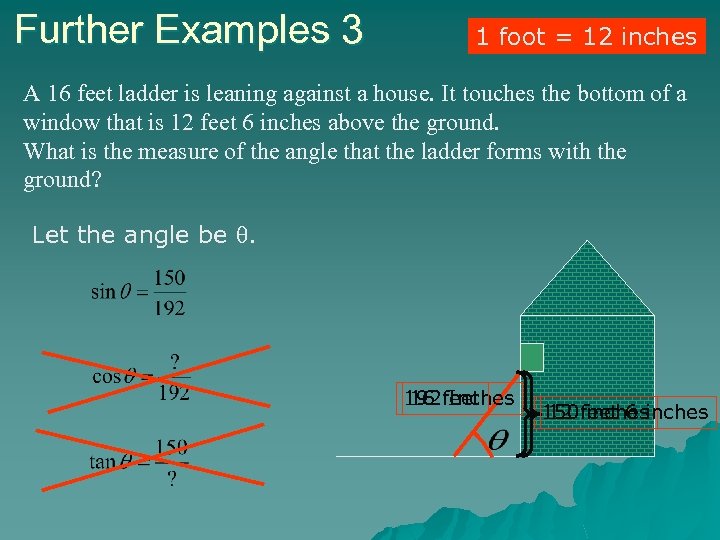Further Examples 3 1 foot = 12 inches A 16 feet ladder is leaning against a house. It touches the bottom of a window that is 12 feet 6 inches above the ground. What is the measure of the angle that the ladder forms with the ground? Let the angle be . 192 feet 16 Inches 150 feet 6 inches 12 inches

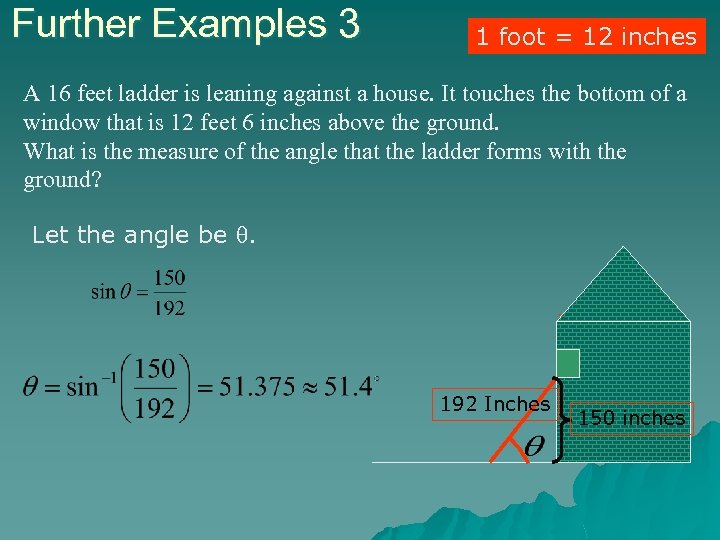Further Examples 3 1 foot = 12 inches A 16 feet ladder is leaning against a house. It touches the bottom of a window that is 12 feet 6 inches above the ground. What is the measure of the angle that the ladder forms with the ground? Let the angle be . 192 Inches 150 inches

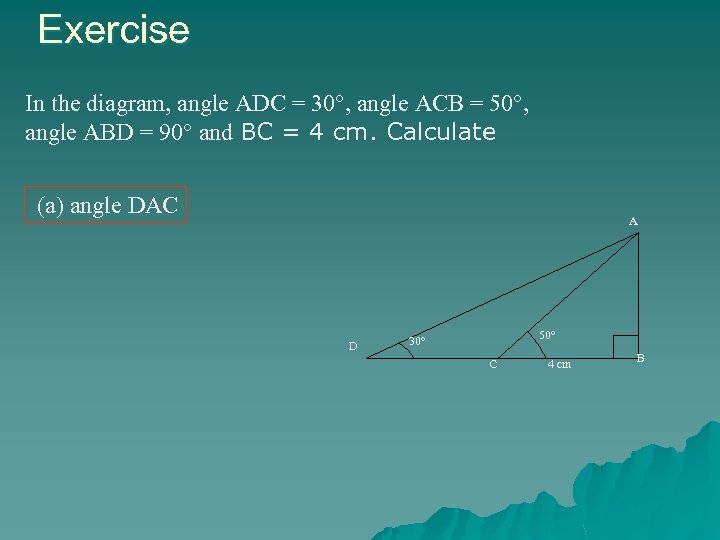Exercise In the diagram, angle ADC = 30°, angle ACB = 50°, angle ABD = 90° and BC = 4 cm. Calculate (a) angle DAC A D 50° 30° C 4 cm B

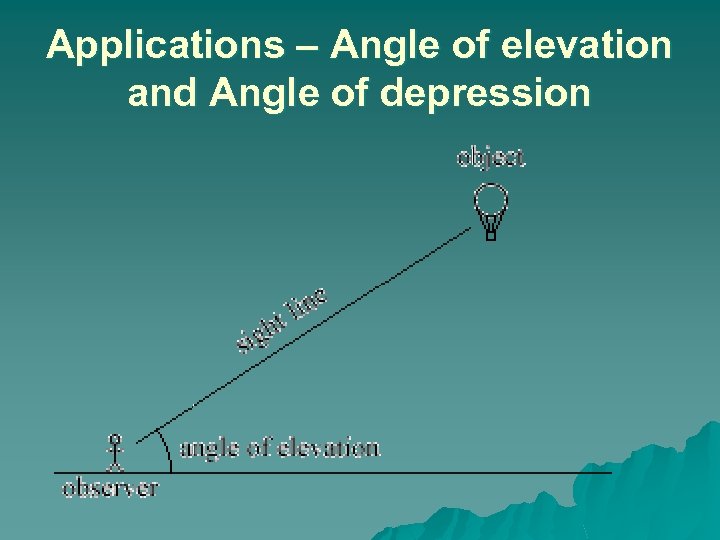Applications – Angle of elevation and Angle of depression

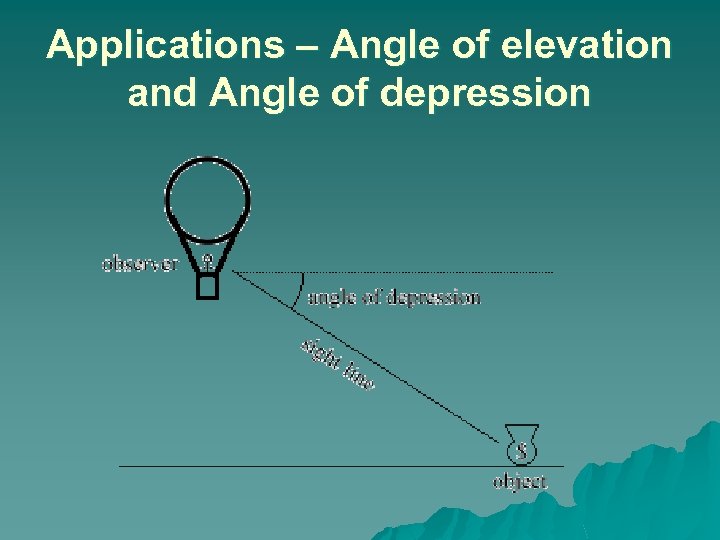Applications – Angle of elevation and Angle of depression

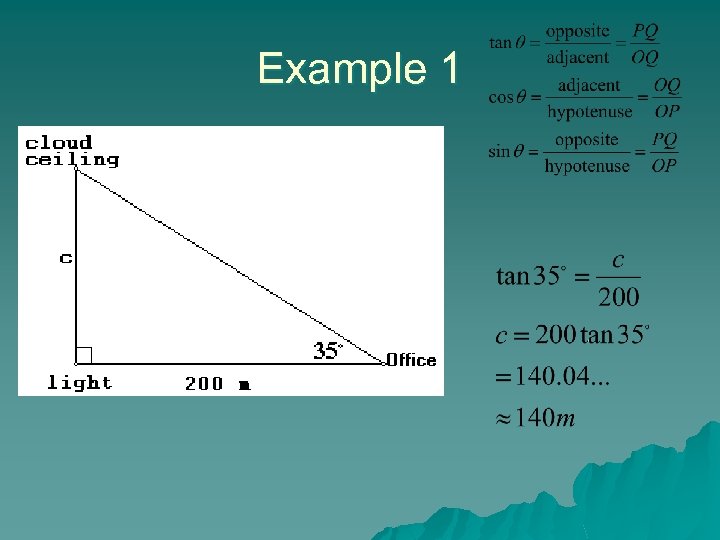Example 1

Example 2 A surveyor is 100 meters from the base of a dam. The angle of elevation to the top of the dam measures. The surveyor's eye-level is 1. 73 meters above the ground. Find the height of the dam.

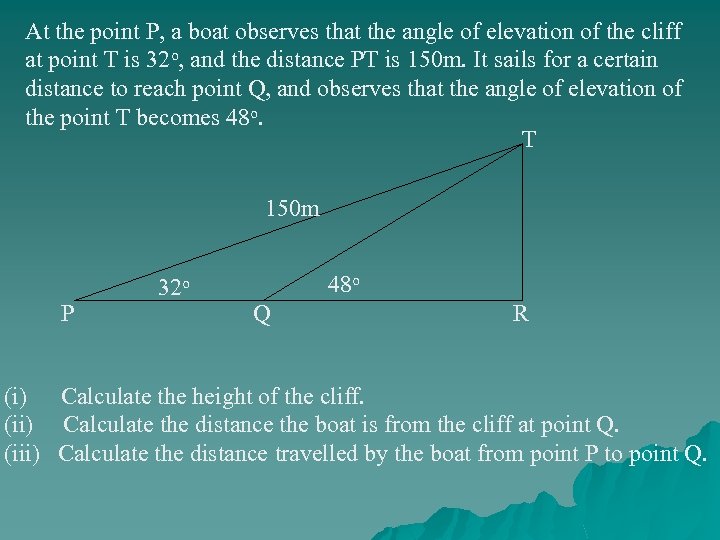At the point P, a boat observes that the angle of elevation of the cliff at point T is 32 o, and the distance PT is 150 m. It sails for a certain distance to reach point Q, and observes that the angle of elevation of the point T becomes 48 o. T 150 m P 32 o 48 o Q R (i) Calculate the height of the cliff. (ii) Calculate the distance the boat is from the cliff at point Q. (iii) Calculate the distance travelled by the boat from point P to point Q.

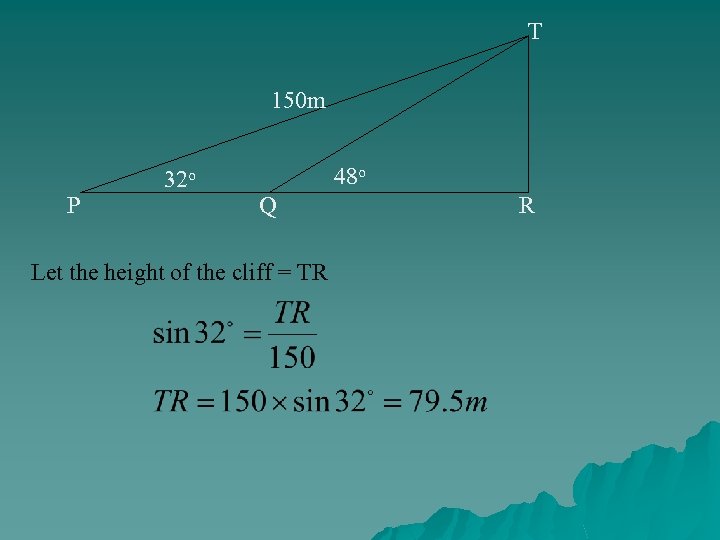T 150 m P 32 o 48 o Q Let the height of the cliff = TR R

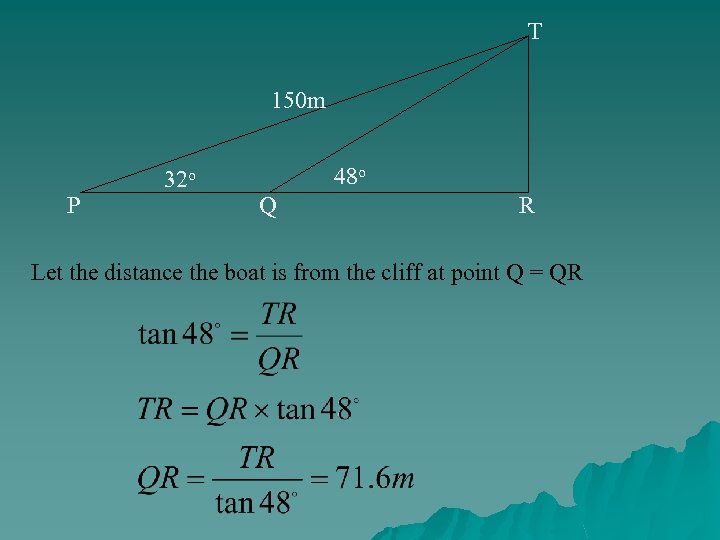T 150 m P 32 o 48 o Q R Let the distance the boat is from the cliff at point Q = QR

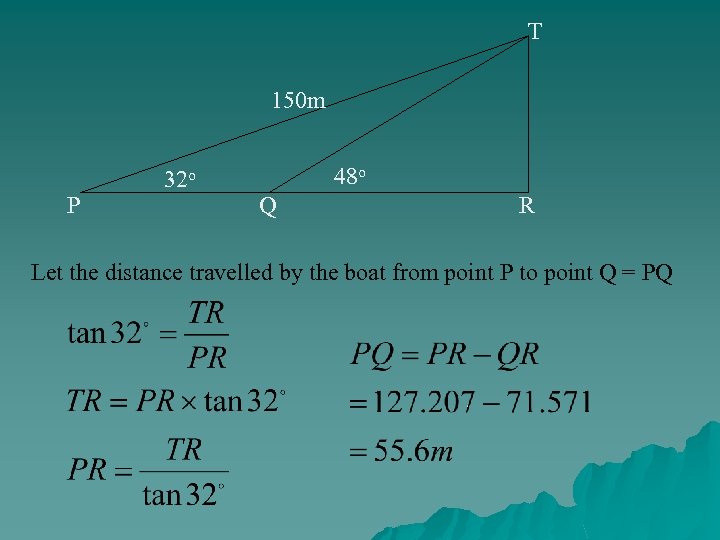T 150 m P 32 o 48 o Q R Let the distance travelled by the boat from point P to point Q = PQ

Trigonometric Ratios of Special Angles: 30°, 45° and 60°. 1 1 2 1 1

Trigonometric Ratios of Complementary Angles. Q c b P a R