Тригонометрические уравнения неравенства и их системы

Тригонометрические уравнения, неравенства и их системы.

• • • Цели. Неформальное усвоение, систематизация, переформулировка, установление связей, умение выделять структуру – развитие мат. культуры.

Виды тригонометрических уравнений по способу их решения 1. 2. 3. 4. 5. a) b) c) Простейшие тригонометрические уравнения и сводящиеся к ним или их совокупностям. Триг. ур-ния, сводящиеся к алгебраическим относительно триг. функции : а) к квадратным (степенным), б)однородные; в) универсальная подстановка. Уравнения вида asinx+bcosx=c(a, b , cєR, a≠ 0, b≠ 0) и сводящиеся к ним. Уравнения , в процессе решения которых используются свойства тригонометрических функций(метод оценки). Искусственные приёмы Подстановка sinx+cosx=t; Домножение и решение произведения косинусов удваивающихся аргументов на 2 nsinα; Дополнение до полного квадрата.

I. Простейшие тригоном. уравнения и сводящиеся к ним • Способы вывода формул решений простейших тр. ур. 1. С помощью координатной окружности. 2. Графическое решение. 3. Аналитический способ: решить уравнение sinx=a ] (|a|≤ 1), ]x 0=α - одно из решений, которое обязательно сущ. , т. к. |a|≤ 1, причём αє[-π/2; π/2] Тогда sin α =a, но sinx=a → sinx=sin α ; sinx-sin α =0; 2 sin (x-α)/2 · ·cos (x- α)/2 =0; • 1. Примеры уравнений, сводимых к простейшим уравнениям или их совокупностям и системам. Произведение (частное)=0

Пример. • Вывод: если ОДЗ сомножителей не совпадают, то есть опасность неравносильного перехода к совокупности уравнений

Основание - теорема (о разложении на множители) f(x)g(x)=0 (1)

• Решение. !!! Система должна быть с разными индексами.

2. Разложение на множители (вынесение общ. множителя, группировка, тож-ва сокращ. умн. ) 2. а. ) с использованием тригонометрической единицы (2 sinx-cosx)(1+cosx)=sin 2 x (1+cosx)(2 sinx - cosx -1 + cosx) = 0; !!! Совокупность тр. ур. может быть с одинаковыми индексами!!! 2. b. ) c использованием формул суммы и разности: sin πx 2= sin π(x 2+2 x) sin πx 2 -sin π(x 2+2 x) =0; 2 cos π(x 2+x)sinπx=0; 3+4 n ≥ 0; n ≥ -¾ → n є N U{0} Ответ. {l; nєNU{0}; lєZ} !!!Совокупность тр. ур. иногда должна быть с разными индексами!!! !для решения уравнений вида sinx=cosx используются формулы приведения!

2. c. )использование преобразования произведения в сумму: • cos 3 xcos 6 x=cos 4 xcos 7 x ответ. {πk/10, kєZ} • tg(x 2 -x)ctg 2=1(2 способа) ответ. • 2 соs 3 x/2 cosx/2=a; ответ. [-9/8; 0]; {±arccos 2. d. ) использование формул понижения степени. sin 2 x+ sin 2 2 x= sin 2 3 x + sin 2 4 x }

4 sin 2 x+3 cos 2 x=5 1 способ. Введение вспомогательного угла (преобразование к виду одной тригонометрической функции) a sinу+b cosy = • a=4; b=3 → √ 25 sin(2 x+arcsin 3/5)=5; Ответ.

4 sin 2 x+3 cos 2 x=5 2 способ. Сведение к однородному. 4· 2 sinxcosx+3(cos 2 x-sin 2 x)-5(cos 2 x+sin 2 x)=0; 4 sinxcosx-4 sin 2 x-cos 2 x=0 - (*) - однородное уравнение 2 степени ]sinx=0, тогда из ур-ния(*): cosx=0, чего при одном и том же х быть не может(из основного тригонометрического тождества)→ →поделим на sin 2 x≠ 0 : ctg 2 x-4 ctgx+4=0; (ctgx-2)2=0; ctgx=2; Ответ. х = arcctg 2+πn, nєZ

4 sin 2 x+3 cos 2 x=5 • 3 способ. Возведение в квадрат. 4 sin 2 x=5 -3 cos 2 x| 2; 16 sin 22 x=25 -30 cos 2 x+9 cos 22 x; 16 -16 cos 22 x=25 -30 cos 2 x+9 cos 22 x; 25 cos 22 x-30 cos 2 x+9=0; (5 cos 2 x-3)2=0; cos 2 x=3/5; !!! Проверка!!! (при возведении в квадрат- взятии неинъективной функции на объединении ОЗ правой и левой частей уравнения - могли появиться лишние корни) 1. ] 2. ] Ответ.

4 sin 2 x+3 cos 2 x=5 4 способ. Универсальная подстановка. х = arctg 1/2+πk, kєZ. !!!Проверка!!! (при тождественном преобразовании, сужающим ОДЗ, можно потерять корни, не вошедшие в новое ОДЗ) ]х=π/2+πk; 4 sin 2(π/2+πk)+3 cos 2(π/2+πk)=4 sin π+3 cos π=0 -3≠ 5

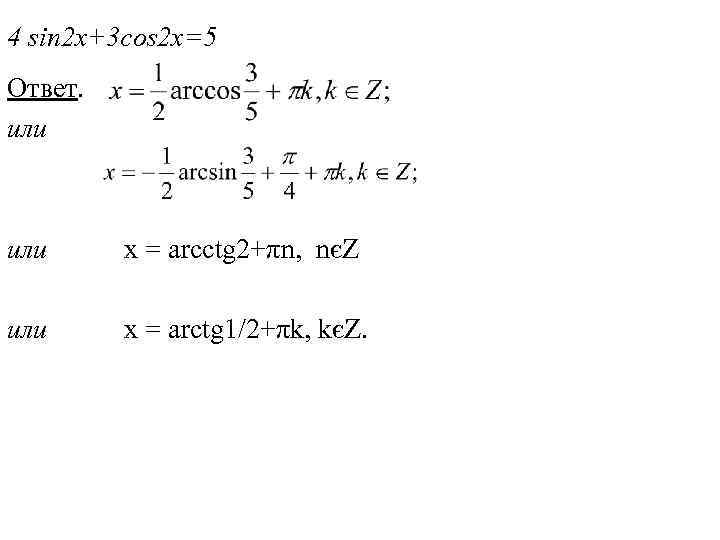4 sin 2 x+3 cos 2 x=5 Ответ. или х = arcctg 2+πn, nєZ или x = arctg 1/2+πk, kєZ.

Уравнения , в процессе решения которых используется метод оценки. • Использование МЗФ a) b) 5 sinx=13 -7 cosx c) 6 сos 2 5 x – 5 cosx + 5 = 0; 6 сos 25 x = 5(cosx-1); 6 сos 25 x ≥ 0 ; cosx-1 ≤ 0; Ответ. Корней нет. • Использование монотонности тригонометрических функций sinx = 2 sin 470 cos 440 sin 470 >sin 450, cos 440>cos 450; 2 sin 470 cos 440 > 2 sin 450 cos 450 =1; корней нет.

sinx+cosx=2 1 способ. Использование ограниченности функций. |sinx|≤ 1 |cosx| ≤ 1 sinx+cosx≤ 2 !!!Используется не столько МЗФ, сколько ограниченность Ответ. Корней нет. 2 способ. Использование МЗФ. Оценим модуль левой части при помощи введения вспомогательной переменной: 3 способ. Поиск наибольшего(наименьшего) значения с помощью производной. у' =cosx-sinx =0|: cosx≠ 0; tgx=1; x=π/4+πn, nєZ T(sinx, cosx)=2π → x= π/4; 5π/4. y(0)=1; y(2π)=1; y(π/4)=√ 2; y(5π/4)= - √ 2 унаиб. = √ 2, т. е. sinx+cosx≤ 2. Ответ. Корней нет.

• Использование алгебраических фактов(сумма квадратов равно 0, только если каждое слагаемое равно 0; формулы сокращенного умножения) ОДЗ: cosx≠ 0 Графически или аналитически Ответ. {-π/3+πk|k=2 n, k, nєZ}

Специальные приёмы • Подстановка sinx±cosx=t, тогда Для уравнений, содержащих сумму(разность) и произведение sin(cos) одинаковых углов. !!! Иногда в правило подстановки включают ограничения на переменную t: |t| ≤ √ 2 !!! Пример. sinx+cosx-sinxcosx=0 ; sinx+cosx=t, тогда t 2 = 1+2 sinxcosx; Тогда t=0|· 2; -2 t-1+t 2=0; t 2 -2 t -1 = 0; sinx+cosx= 1 -√ 2 – введение вспомогательной переменной. Ответ.

Обратные тригонометрические функции Арксинусом числа р называется число из промежутка [-π/2; π/2], синус которого равен р, если рє[-1; 1] Основные формулы. I. sin(arcsin a)=a , … II. аrcsin(sin a)=a, если aє [-π/2; π/2], … III. arcsin(-a)= - arcsin a, arctg(-a)=-arctg a, arccos(-a)=π - arccos a, arcctg(-a)=π - arcctg a, IV. arcsin a+ arccos a= π/2, arctg a+ arcctg a = π/2

Уравнения, содержащие переменную под знаком аркфункции. I Простейшие уравнения, решаемые по определению. Пример. arcsin 2 x = 2π/3 Решение. (стандартное) 1. ООФ: |2 x|≤ 1, |x≤½| 2. По определению 2 x = sin 2π/3; 2 x = √ 3/2; x= √ 3/4 ≈0, 4 є ООФ Ответ. √ 3/4 Решение. (правильное) 1. МЗФ: лев. ч. : arcsin 2 x є[-π/2; π/2], Ответ. Корней нет. 2π/3 є(π/2; 3π/2).

II Уравнения, способ решения которых основан на нахождении значений тригонометрических функций от обеих частей уравнения Основные этапы решения. 1. Найти ОДЗ, как пересечение ООФ левой и правой частей уравнения. 2. Найти объединение МЗФ левой и правой частей уравнения с учётом ОДЗ. 3. Выбрать тригонометрическую функцию, монотонную на объединении МЗФ левой и правой частей уравнения. 4. Взять выбранную функцию от обеих частей уравнения. P. S. Если нет функции, монотонной на объединении МЗФ левой и правой частей уравнения, то a) сделать проверку; b) можно попробовать преобразовать уравнение при помощи переноса слагаемых из одной части в другую или деления на число и т. д.

Пример. 1. 2. arcsin x 2 – arccos x = 0 ОДЗ: МЗ : 0 ≤ arcsin x 2 ≤ π/2 - π ≤ - arccos x ≤ 0 - π ≤ arcsin x 2 – arccos x≤ π/2 - нет таких промежутков монотонности → преобразуем уравнение arcsin x 2 = arccos x 1. ОДЗ: 2. МЗ 2 : (0 ≤ arcsin x 2 ≤ π/2 ; 0 ≤ arccos x ≤ π ) → МЗ 2 = (0; π) → у=cos α – монотонна на (0; π). 3. соs(arcsin x 2 )=cos( arccos x), ] arcsin x 2 =t, sin t = x 2, t є (0; π/2) с учётом огр. ответ.

Пример. arcsin 2 x+arcsinx=π/3 1. ОДЗ: -1≤ 2 х ≤ 1; -½ ≤ х ≤ ½ 2. МЗ: -π/6≤ arcsin x ≤ π/6 - π/2 ≤ arcsin 2 x ≤ π/2 - 2π/3 ≤ arcsin 2 x + arcsin x≤ 2π/3 - нет таких промежутков монотонности → ØПреобразование уравнения → I способ решения: arcsin 2 x = π/3 – arcsinx Л. ч. : - π/2 ≤ arcsin 2 x ≤ π/2; Пр. ч. : -π/6 ≤ -arcsin x ≤ π/6; |+π/3 π/6≤ π/3 - arcsin x ≤ π/2; МЗ: [- π/2; π/2]- промежуток монотонности функции у = sin x → ответ

Пример. arcsin 2 x+arcsinx=π/3. ØБолее строгая оценка области изменения аргумента → II способ решения Д. у. : аркфункции отличаются только растяжением вдоль оси ОХ → либо одновременно положительны, либо π/2 одновременно отрицательны. у=arcsinx у=arcsin 2 x -½ ½ -1 1 - π/2 → их сумма может быть положительна только при положительном аргументе : х≥ 0; 0≤ х ≤ ½; → 0 ≤ arcsin x ≤ π/6; 0≤ arcsin 2 x ≤ π/2 0 ≤ arcsin 2 x +arcsin x ≤ 2π/3; МЗ: [0; π]- промежуток монотонности функции у = cos x →

III способ решения. Берут любую удобную функцию от обеих частей уравнения с последующей проверкой. • Проверка.

III Уравнения, сводимые к простейшим алгебраически и с помощью основных формул аркфункций. Пример. аrccosx - arcsinx =π/6 ОДЗ: |x|≤ 1 (π/2 - arcsinx) - arcsinx = π/6 ; 2 arcsinx = π/2 - π/6 ; Arcsinx = π/6; x=1/2. IV Уравнения, решаемые методом оценки Пример. 3 arccos(7 x-1)+2 arctg(x+8)=2 arcsin(-1) = 2· (-π/2)=- π 0 ≤ 3 arccos(7 x-1) ≤ 3π 2· (-π/2) < 2 arctg(x+8) < 2· π/2 -π< 3 arccos(7 x-1)+2 arctg(x+8)<4π !!! Строгие неравенства Ответ. Корней нет.

V Уравнения, решаемые графически. Пример. 3 arcsinx + πx – π = 0; 3 arcsinx = - πx + π ; ] x = ½: 3 arcsin½ + π·½ – π = = 3π/6+ π/2– π = 0 3π/2 π -1 y= 3 arcsinx ½ 1 y=π-πx -3π/2

Неравенства, содержащие переменную под знаком аркфункции. • Проверку сделать невозможно → один из выходов – метод интервалов. Пример. аrcsin 2 x + arcsinx < π/3; ОДЗ: -½ ≤ х ≤ ½ аrcsin 2 x + arcsin x - π/3 <0; -½ + аrcsin 2 x + arcsin x - π/3 =0; ; ] x = 0 → arcsin 0 + arcsin 0 - π/3 = 0 + 0 - π/3 < 0. Ответ. [-½; ) ½