Тригонометрические функции Работу выполнили студентки ФСПО 3 курса

Тригонометрические функции Работу выполнили студентки ФСПО 3 курса 34 группы Савельева М. А. Васильева А. А.

Содержание Введение Определение тригонометрических функций Свойства тригонометрических функций Простейшие тождества Непрерывность Чётность Периодичность Формулы приведения Формулы сложения Формулы для кратных углов 1. Формулы двойного угла 2. Формулы тройного угла 3. Прочие формулы для кратных углов

Содержание Формулы половинного угла Произведения 1. Формулы для произведений функций двух углов 2. Формулы для произведений синусов и косинусов трёх углов Степени Суммы Однопараметрическое представление Знаки тригонометрических функций Значения тригонометрических функций Выражение тригонометрических функций через одну из них того же аргумента

Содержание Преобразование суммы тригонометрических функций Выражение тригонометрической функции через тангенс половинного аргумента Преобразование степеней синуса и косинуса График функции y = sin(x) Основные свойства функции y = sin(x). Функция косинус y = cos(x). Свойства функции косинус y = cosx Основные свойства функции y = tg(x). График функции y = tg(x). Функция котангенс y = ctg(x). Свойства функции котангенс y = ctgx.

Содержание Способы определения Определение тригонометрических функций через окружность Производные и интегралы Заключение Литература

Введение Тригонометрия - слово греческое и в буквальном переводе означает измерение треугольников В данном случае измерение треугольников следует понимать как решение треугольников, т. е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников. Возникновение тригонометрии связано с землемерением, астрономией и строительным делом. Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э. ) и Клавдием Птолемеем (2 в. н. э. ). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.

Определение тригонометрических функций Тригонометрические функции — математические функции от угла. Они важны при изучении геометрии, а также при исследовании периодических процессов. Обычно тригонометрические функции определяют как отношения сторон прямоугольного треугольника или длины определённых отрезков в единичной окружности.

К тригонометрическим функциям относятся: прямые тригонометрические функции синус (sin x) косинус (cos x) производные тригонометрические функции тангенс (tg x) котангенс (ctg x) другие тригонометрические функции секанс (sec x) косеканс (cosec x)

Свойства тригонометрических функций Простейшие тождества Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем: Это соотношение называется тригонометрическим тождеством. основным

Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:

Непрерывность Синус и косинус — непрерывные функции. Тангенс и секанс имеют точки разрыва котангенс и косеканс —

Чётность Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:

Периодичность Функции — периодические с периодом 2π; функции — c периодом π.

Формулы приведения Формулами приведения называются формулы следующего вида:

Формулы сложения Значения тригонометрических функций суммы и разности двух углов:

Формулы для кратных углов Формулы двойного угла:

Формулы тройного угла

Прочие формулы для кратных углов

Формулы половинного угла:

Произведения Формулы для произведений функций двух углов

Формулы для произведений синусов и косинусов трёх углов

Степени

Суммы

Однопараметрическое представление Все тригонометрические функции можно выразить через тангенс половинного угла.

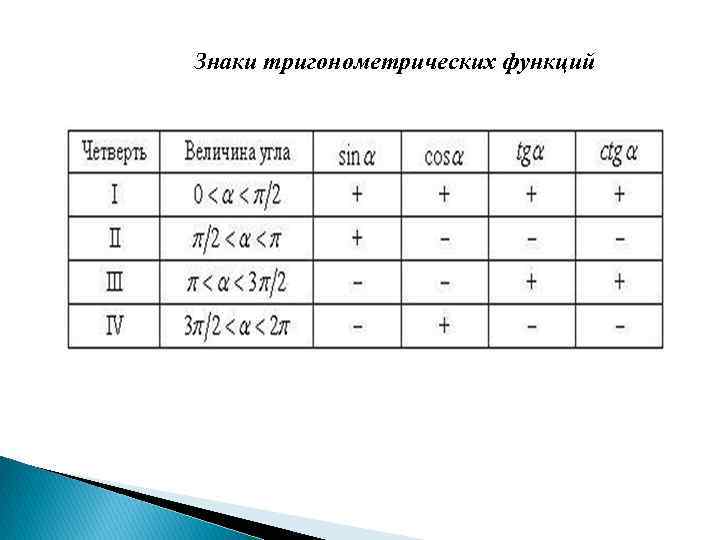
Знаки тригонометрических функций

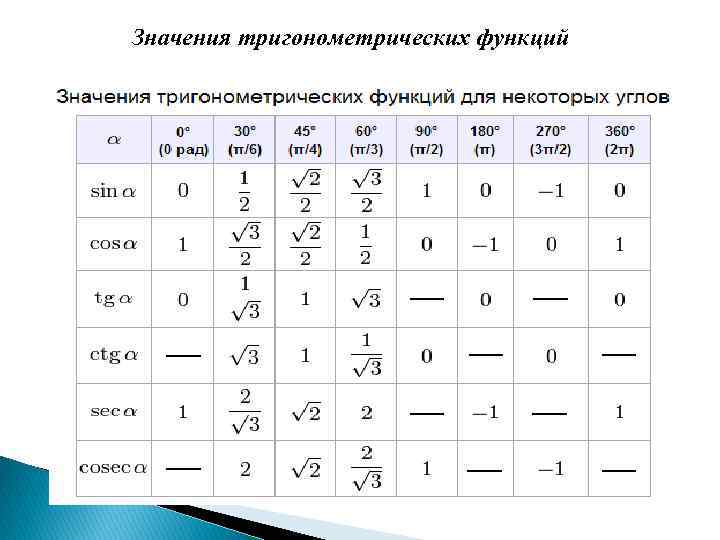
Значения тригонометрических функций

Выражение тригонометрических функций через одну из них того же аргумента Через

Через

Преобразование суммы тригонометрических функций

Преобразование произведения тригонометрических функций в сумму

Выражение тригонометрической функции через тангенс половинного аргумента

Преобразование степеней синуса и косинуса

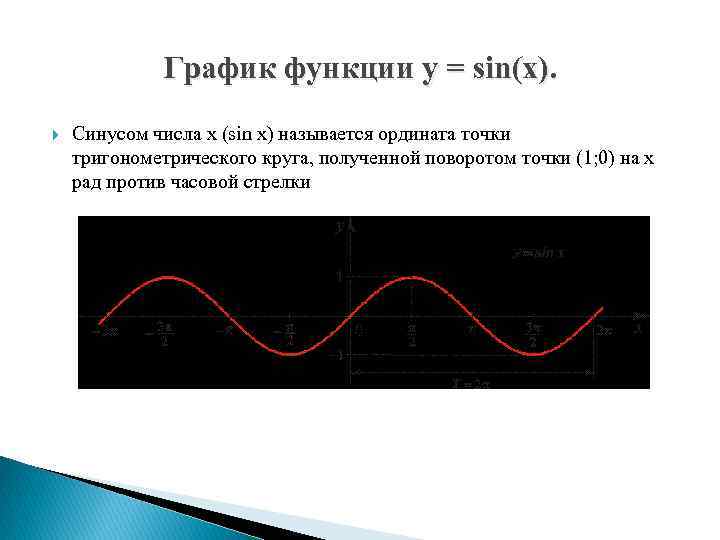
График функции y = sin(x). Синусом числа х (sin x) называется ордината точки тригонометрического круга, полученной поворотом точки (1; 0) на х рад против часовой стрелки

Основные свойства функции y = sin(x). 1. Областью определения функции является множество всех действительных чисел: 2. Областью значений функции является множество значений всех чисел отрезка на интервале [− 1; 1], значит, синус — функция ограниченная. 3. Функция нечетная: График нечетной функции симметричен относительно начала координат — точки О. 4. Функция периодическая с наименьшим положительным периодом T = 2π:

8. Функция возрастает от − 1 до 1 на промежутках 9. Функция убывает от 1 до − 1 на промежутках: 10. Наибольшее значение sin x = 1 функция приобретает в точках: 11. Наименьшее значение sin x = − 1 функция приобретает в точках:

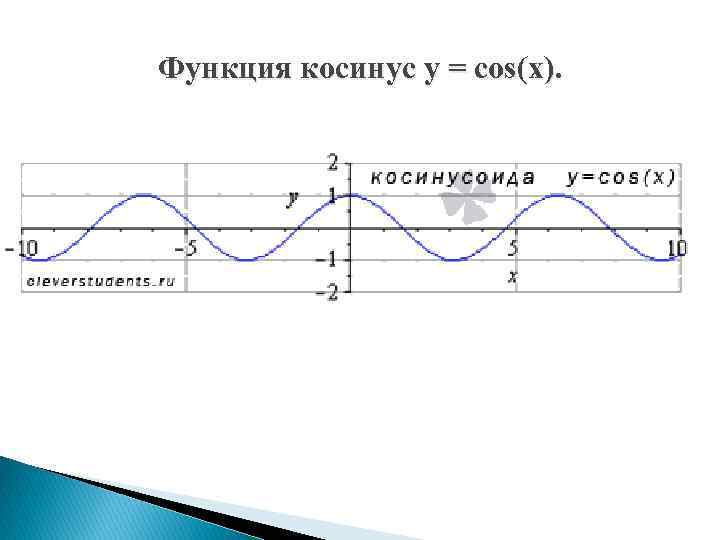
Функция косинус y = cos(x).

Свойства функции косинус y = cosx 1. Область определения функции косинус: 2. Наименьший положительный период функции y = cosx равен двум пи: 3. Функция обращается в ноль при где , Z – множество целых чисел. 4. Область значений функции косинус представляет интервал от минус единицы до единицы включительно: . 5. Функция косинус - четная, так как. 6. Функция убывает при возрастает при 7. Функция y = cosx имеет локальные максимумы в точках локальные минимумы в точках

Основные свойства функции y = tg(x). 1. Областью определения функции является множество всех действительных чисел кроме: 2. Областью значений функции является множество значений всех чисел, таким образом, тангенс — функция неограниченная. 3. Функция нечетная: 4. График нечетной функции симметричен относительно начала координат — точки О. 5. Функция периодическая с наименьшим положительным периодом T = π, то есть, из области определения.

График функции y = tg(x).

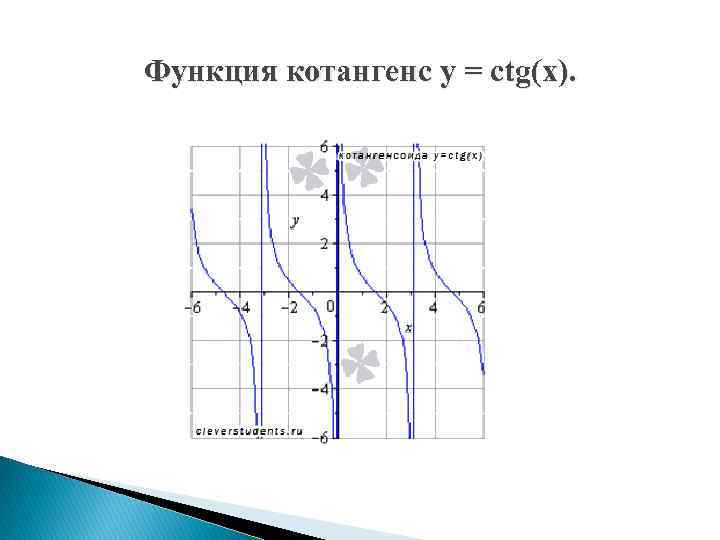
Функция котангенс y = ctg(x).

Свойства функции котангенс y = ctgx. 1. Область определения функции котангенс: Z – множество целых чисел. 2. Поведение на границе области определения 3. Наименьший положительный период функции y = ctgx равен пи: 4. Функция обращается в ноль при 5. Область значений функции котангенс:

6. Функция нечетная, так как 7. Функция y = ctgx убывает при 8. Функция котангенс вогнутая при выпуклая при 9. Координаты точек перегиба 10. Наклонных и горизонтальных асимптот нет.

Способы определения Геометрическое определение Чтобы определить тригонометрические функции произвольного угла α, возьмём произвольный прямоугольный треугольник, содержащий угол α. Стороны этого треугольника мы будем называть так: Гипотенуза — сторона, противолежащая прямому углу, самая длинная сторона в треугольнике. В данном случае, сторона c. Противолежащий катет — катет, лежащий напротив угла. Например, катет a — противолежащий по отношению к углу A. Прилежащий катет — катет, являющийся стороной угла. Например, катет b — прилежащий по отношению к углу A.

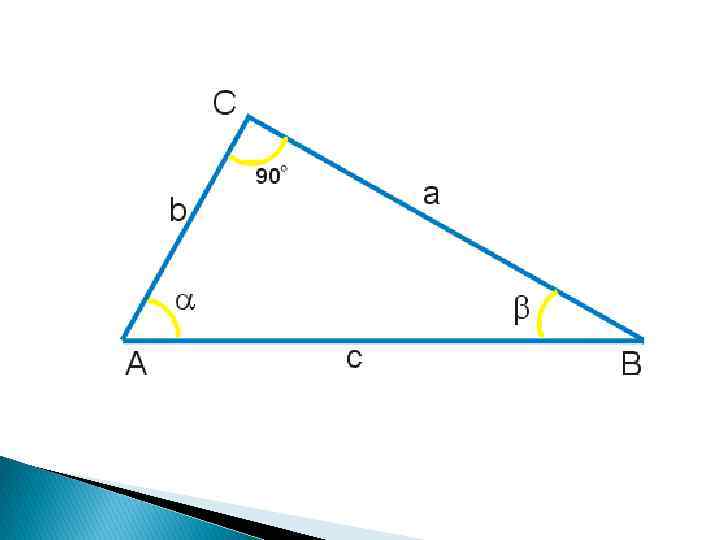
Синус угла — отношение противолежащего катета к гипотенузе: Косинус угла — отношение прилежащего катета к гипотенузе: Тангенс угла — отношение противолежащего катета к прилежащему: Котангенс угла — отношение прилежащего катета к противолежащему: Секанс угла — отношение гипотенузы к прилежащему катету Косеканс угла — отношение гипотенузы к противолежащему катету:

Определение тригонометрических функций через окружность Пусть на плоскости задана прямоугольная система координат с началом в точке O и с осями OX и OY. Возьмём в этой системе координат окружность с центром в точке O и радиусом, равным единице. Пусть отрезок OA поворачивается на произвольный угол вокруг центра O. .

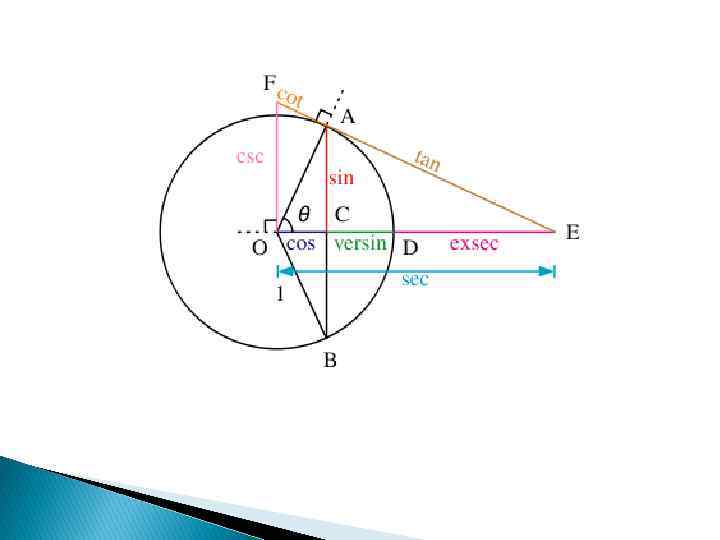
Синусом угла называется отношение ординаты точки A к длине отрезка OA. Обозначают Косинусом угла называется отношение абсциссы точки A к длине отрезка OA. Обозначают Тангенсом угла называется отношение ординаты точки A к абсциссе точки A. Обозначают Котангенсом угла называется отношение абсциссы точки A к ординате точки A. Обозначают

Косекансом угла называется отношение длины отрезка OA к ординате точки A. Обозначают Секансом угла называется отношение длины отрезка OA к абсциссе точки A. Обозначают

Производные и интегралы Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:

Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:

Заключение История названий Линия синуса у индийских математиков первоначально называлась «арха-джива» ( «полутетива» , то есть половина хорды), затем слово «арха» было отброшено и линию синуса стали называть просто «джива» . Арабские переводчики не перевели слово «джива» арабским словом «ватар» , обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба» . Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й» , арабы стали произносить название линии синуса «джайб» , что буквально обозначает «впадина» , «пазуха» . При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.

Литература Бронштейн И. Н. , Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7 -е, стереотипное. — М. : Государственное издательство техникотеоретической литературы, 1967. — С. 179— 184. Г. Б. Двайт Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4 -е изд. — М. : Наука, 1973. — С. 70— 102. [править] Ссылки Gonio. Lab — прояснённая единичная окружность, тригонометрические и гиперболические функции (Java Web Start) Weisstein, Eric W. Тригонометрические функции (англ. ) на сайте Wolfram Math. World. Онлайн калькулятор: вычисление значений тригонометрических функций Интерактивная карта значений тригонометрических функций