Тригонометрические функции и формулы Автор Календарева Н Е

Тригонометрические функции и формулы Автор Календарева Н. Е. © 2011 г.

План 1. Определение функции у = sinx и функции у = cosx 2. Определение функции у = tgx и функции у = ctgx 3. Теоремы сложения 4. Формулы двойного аргумента 5. Формулы половинного аргумента 6. Формулы понижения степени

Продолжение плана 7. Формулы приведения 8. Формулы преобразования суммы двух функций в их произведение и обратно, произведения в сумму

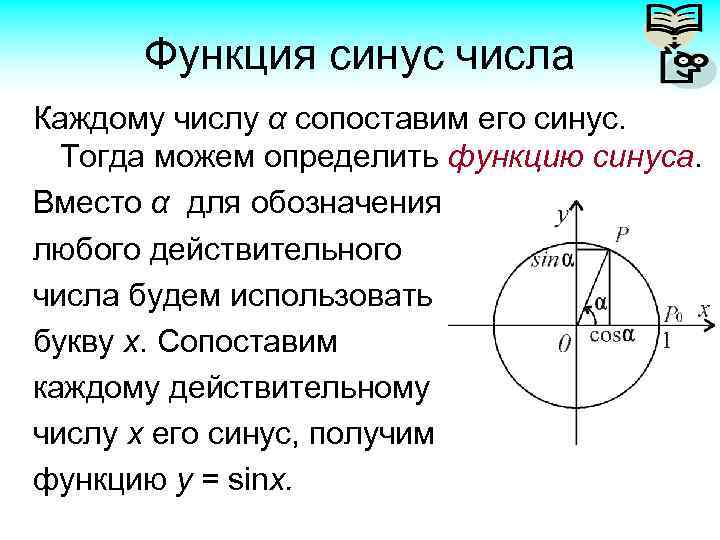Функция синус числа Каждому числу α сопоставим его синус. Тогда можем определить функцию синуса. Вместо α для обозначения любого действительного числа будем использовать букву х. Сопоставим каждому действительному числу х его синус, получим функцию у = sinx.

Область определения Аналогично определяется функция косинуса числа. То есть сопоставим числу х его косинус, получим функцию у = cosx. Каждая из функций у = sinx и у = cosx определена на всей числовой прямой. Областью определения этих двух функций является множество R.

Множество значений Множеством значений функций синус и косинус является отрезок [ – 1; 1], так как и ординаты, и абсциссы точек единичной окружности принимают все значения от – 1 до 1. Пишут так | sinx | 1 и | cosx | 1. Вопрос. Верна ли запись sin x = 2?

Функции тангенс и котангенс Числовые функции, заданные равенствами у = tg x и y = ctg x, называются соответственно тангенсом и котангенсом. Областью определения тангенса является множество всех чисел х, для которых cos x ≠ 0. Областью определения котангенса является множество всех чисел х, для которых sin x ≠ 0.

Множество значений тангенса и котангенса – вся числовая прямая, т. е. R.

Четность, нечетность тригонометрических функций Синус, тангенс и котангенс являются нечетными функциями, а косинус является четной функцией, т. е. sin(−α) = − sin α; cos(−α) = cos α; tg(−α) = − tg α; ctg(−α) = − ctg α.

Теоремы сложения Теорема. Для любых действительных чисел α и β справедливо равенство cos (α + β) = cos α ∙cos β − sin α ∙sin β. Для док-ва понадобится формула длины отрезка, концы которого заданы своими координатами: точки А(х1; у1) и В(х2; у2). А В Длина АВ =

Доказательство Δ АОР = Δ NОМ (1 признак) => РА =MN. Координаты точек: Р(cos(α + β); sin (α + β)); A(1; 0); M(cos α; sin α); N(cos(−β); sin(−β)) = = N(cosβ; sin(−β)).

PA 2 = MN 2 PA 2 = (cos(α + β) − 1)2 + (sin(α + β)) − 0)2 = = 1 − 2 cos(α + β) + cos 2(α + β) + sin 2(α + β) = = 1 − 2 cos(α + β) + 1 = 2 − 2 cos(α + β). MN 2 = (cos α − cos β)2 + (sin α − sin(− β))2 = = cos 2α − 2 cosα cos β + cos 2β + sin 2α − − 2 sinα sin(− β) + sin 2 (− β) =1 − 2 cos α cos β + + 1 + 2 sin α sin β = 2 − 2 cos α cos β + 2 sin α sin β. Подставим в равенство PA 2 = MN 2.

PA 2 = MN 2 2 − 2 cos(α + β) = 2 − 2 cosα cos β + 2 sinα sin β; − 2 cos(α + β) = − 2 cosα cos β + 2 sinα sin β; Сократим на − 2: cos (α + β) = cos α ∙cos β − sin α ∙sin β. (1) Теорема доказана.

Теорема 2 cos (α − β) = cos α ∙cos β + sin α ∙sin β Док-во. Заменим в доказанной формуле cos (α + β) = cos α ∙cos β − sin α ∙sin β число β на число β 1 = − β. Получим cos (α + β 1) = cos α ∙cos β 1 − sin α ∙sin β 1 или cos (α − β) = cos α ∙cos(−β) − sin α ∙sin(− β). Учитывая, что cos(−β) = cosβ и sin(− β) = −sinβ, cos (α − β) = cos α ∙cosβ + sin α ∙sin β. (2)

Получим формулы приведения из (1) cos (α + β) = cos α ∙cos β − sin α ∙sin β (1) Подставим β = π : cos (α + π) = cos α ∙cos π − sin α∙sin π = − cos α. β = π/2 : cos (α + π/2 ) = cos α∙cos π/2 − sin α∙sin π/2 = = − sin α. Итак, cos (π + α) = − cos α cos (π/2 + α) = − sin α

Получим формулы приведения из (2) cos (α − β) = cos α ∙cosβ + sin α ∙sin β (2) Подставим β = π/2 : cos (α − π/2) = cos α ∙cos π/2 + sin α ∙sin π/2 = = sin α. Или sin α = cos (π/2 − α). Подставим α = π/2 − α 1, получим cos (π/2 − α 1)) = sin(π/2 − α 1) или cos α 1 = sin(π/2 − α 1).

Таким образом, sin α = cos (π/2 − α) cos α = sin(π/2 − α). (3) (4)

Теоремы сложения для синуса sin(α + β) = sinα ∙cos β + cos α ∙sin β (5) sin(α − β) = sinα ∙cos β − cos α ∙sin β (6) Док-во. Из формулы (3) sin(α + β) = cos (π/2 − (α + β)) = = cos((π/2 − α)− β) = = cos (π/2 − α)∙cos β + sin(π/2 − α) ∙sin β = = sin α∙cos β + cosα ∙sin β. Итак, sin(α + β) = sinα ∙cos β + cos α ∙sin β

Подставим в формулу (5) вместо β число −β. sin(α + β) = sinα ∙cos β + cos α ∙sin β (5) Получим формулу (6): sin(α − β) = sinα ∙cos β − cos α ∙sin β (6)

Формулы двойного аргумента Подставим в формулу (1) вместо β число α: cos (α + α) = cos α ∙cos α − sin α ∙sin α cos 2α = cos 2α − sin 2α (7) Аналогично подставим в формулу (5): sin(α + α) = sinα ∙cos α + cos α ∙sin α sin 2α = 2 sinα ∙cosα (8)

Формулы половинного аргумента Подставим в формулы (7), (8) вместо α число α/2. (α = 2∙(α/2)) Получим cosα = cos 2α/2 − sin 2α/2 sinα = 2 sinα/2 ∙cosα/2 (9) (10)

Формулы понижения степени Имеем cos 2α = cos 2α − sin 2α. Из тригон. единицы sin 2α = 1− cos 2α = cos 2α − (1 – cos 2α ) = 2 cos 2α − 1. Отсюда 2 cos 2α = 1 + cos 2α. Или

Формулы понижения степени Имеем cos 2α = cos 2α − sin 2α. Из тригон. единицы cos 2α = 1− sin 2α = 1− 2 sin 2α. Отсюда 2 sin 2α = 1 − cos 2α. Или

Преобразование произведений синуса и косинуса в суммы Выведем три формулы преобразования произведений синуса и косинуса в суммы. 1) sinx cosy; 2) sinx siny; 3) cosx cosy.

Преобразование произведений в суммы (1 -я формула: синус умножить на косинус) sin(x + y) = sinx cosy + siny cosx. sin(x − y) = sinx cosy − siny cosx. Сложим оба равенства, получим sin(x + y) + sin(x − y) = 2 sinx cosy, или 2 sinx cosy = sin(x + y) + sin(x − y). sinx cosy = (sin(x + y) + sin(x − y))

Преобразование произведений в суммы (2 -я формула: синус умножить на синус) cos(x + y) = cosx cosy − sinx siny. cos(x − y) = cosx cosy + sinx siny. Вычтем из второго равенства первое cos(x − y) − cos(x + y) = 2 sinx siny. Или sinx siny = (cos(x − y) − cos(x + y) ).

Преобразование произведений в суммы (3 -я формула косинус умножить на косинус) cos(x + y) = cosx cosy − sinx siny. cos(x − y) = cosx cosy + sinx siny. Сложим оба равенства, получим cos(x + y) + cos(x − y) = 2 cosx cosy. Или cosx cosy = (cos(x + y) + cos(x − y) ).

Выведем четыре формулы преобразования сумм синуса и косинуса в произведения. (сначала для суммы синусов sinx + siny ). Введем вспомогательные числа α и β. Обозначим α = (х + у)/2; β = (х − у)/2. Сложим почленно: α + β = х/2 + y/2 + х/2 − y/2 = x.

Сумма синусов в произведение Аналогично вычтем: α − β = у. Или х = α + β, у = α − β. sinx = sin(α + β) = sinα ∙cos β + cos α ∙sin β. siny = sin(α − β) = sinα ∙cos β − cos α ∙sin β. Сложим почленно: sinx + siny = 2 sin α ∙cos β; или sinx + siny = 2 sin((х + у)/2) ∙cos((х − у)/2).

Разность синусов в произведение sinx = sin(α + β) = sinα ∙cos β + cos α ∙sin β. siny = sin(α − β) = sinα ∙cos β − cos α ∙sin β. Вычтем почленно из 1 -го равенства второе: sinx − siny = 2 cos α ∙sin β; или sinx − siny = 2 sin((х − у)/2) ∙cos((х + у)/2).

Сумма косинусов в произведение cosx = cos(α + β) = cosα ∙cos β − sin α ∙sin β. cosy = cos(α − β) = cosα ∙cos β + sin α ∙sin β. Сложим cosx + cosy = 2 cosα ∙cos β ; или cosx + cosy = 2 cos(х + у)/2∙cos(х − у)/2.

Разность косинусов в произведение cosx = cos(α + β) = cosα ∙cos β − sin α ∙sin β. cosy = cos(α − β) = cosα ∙cos β + sin α ∙sin β. Вычтем cosx − cosy = − 2 sin α ∙sin β ; или cosx − cosy = − 2 sin(х + у)/2∙sin(х − у)/2. Или cosx − cosy = 2 sin(х + у)/2∙sin(y − x)/2.

Формулы приведения Шесть тригонометрических функций принято записывать в такой упорядоченный ряд: sinx, cosx, tgx, ctgx, secx, cosecx Функции cosx, ctgx, cosecx принято называть кофункциями. Синус – косинус. Тангенс – котангенс. Кофункция от косинуса есть синус.

Формулы приведения (определение) Формулами приведения называется группа формул, выражающих тригонометрические функции чисел π/2 ± α, π ± α, 3π/2 ± α, 2π ± α через тригонометрические функции аргумента α. Имя функции сохраняется для аргументов π ± α, 2π ± α.

Формулы приведения (правило) Имя функции меняется на кофункцию для аргументов π/2 ± α, 3π/2 ± α. Например, cos (π/2 − α) = sin α (см. формулу (3)). Но cos (π/2 + α) = − sin α. Как определить знак правой части?

Формулы приведения (правило) Мысленно предполагаем, что число α расположено в 1 -й четверти. И находим, в какой четверти лежит число π/2 ± α, 3π/2 ± α, π ± α, 2π ± α. Затем определяем знак функции, стоящей в левой части. Знак правой части определяется по знаку левой части.

Вернемся к примеру cos (π/2 + α) = − sin α Число (π/2 + α) находится во второй четверти, в ней косинус отрицателен. Предполагая, что число α (0; π/2), определите, в какой четверти находится аргумент и чему равны следующие функции.

Примеры 1. sin(π − α) Ответ: вторая четверть, sin α 2. cos(π + α) Ответ: третья четверть, − cosα. 3. tg(π/2 + α) Ответ: вторая четверть, −ctgα. 4. sin(3π/2 − α) Ответ: третья четверть, − cosα.

Примеры на формулы приведения 1. cos(3π/2 − α) Ответ: − sin α 2. tg(3π/2 + α) = Ответ: − ctg α 3. sin(π + α) = Ответ: − sin α 4. cos(3π/2 + α) = Ответ: sin α

Домашнее задание 1. Переписать все формулы в блокнот 2. Принести блокнот и показать формулы (на отметку) 3. Уметь выводить формулы тройного аргумента