Тригонометрические формулы Синусом угла называется ордината точки

Тригонометрические формулы

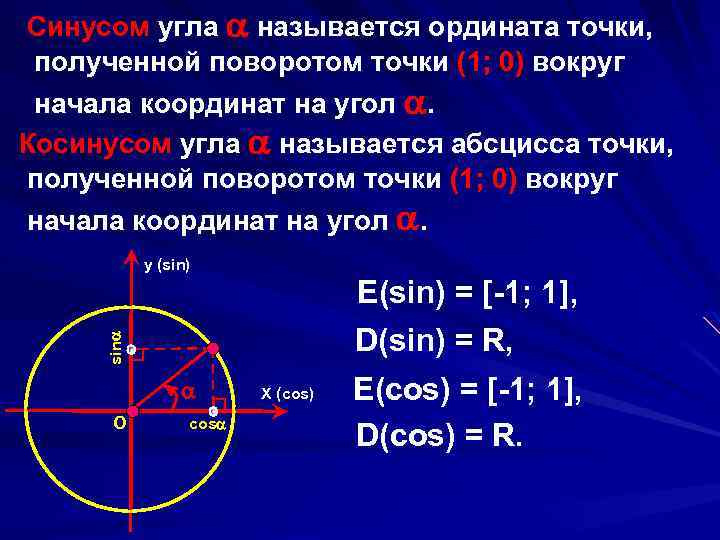Синусом угла называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол . Косинусом угла называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол . y (sin) E(sin) = [-1; 1], sin D(sin) = R, O cos X (cos) E(cos) = [-1; 1], D(cos) = R.

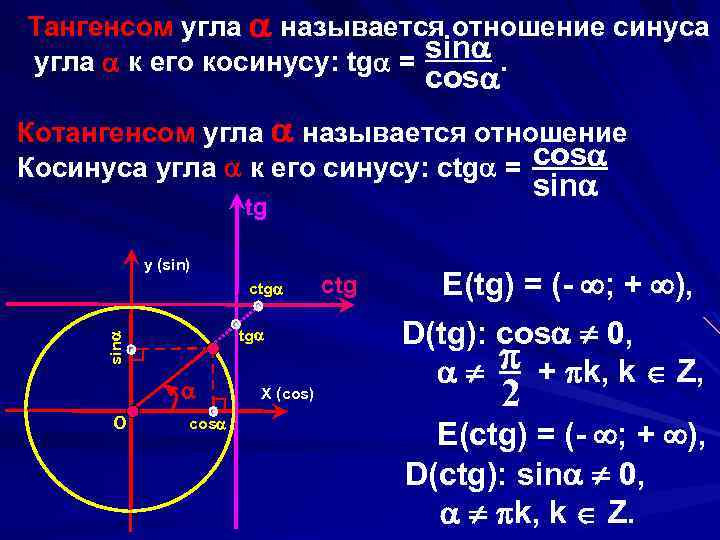Тангенсом угла называется отношение синуса угла к его косинусу: tg = sin . cos Котангенсом угла называется отношение Косинуса угла к его синусу: ctg = cos sin tg y (sin) ctg sin tg O cos X (cos) ctg E(tg) = (- ; + ), D(tg): cos 0, + k, k Z, 2 E(ctg) = (- ; + ), D(ctg): sin 0, k, k Z.

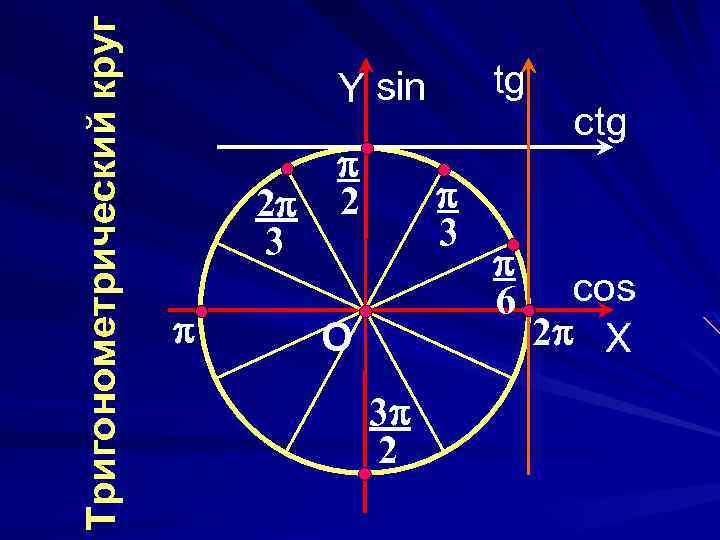Тригонометрический круг tg Y sin 2 3 2 3 O 3 2 6 ctg cos 2 X

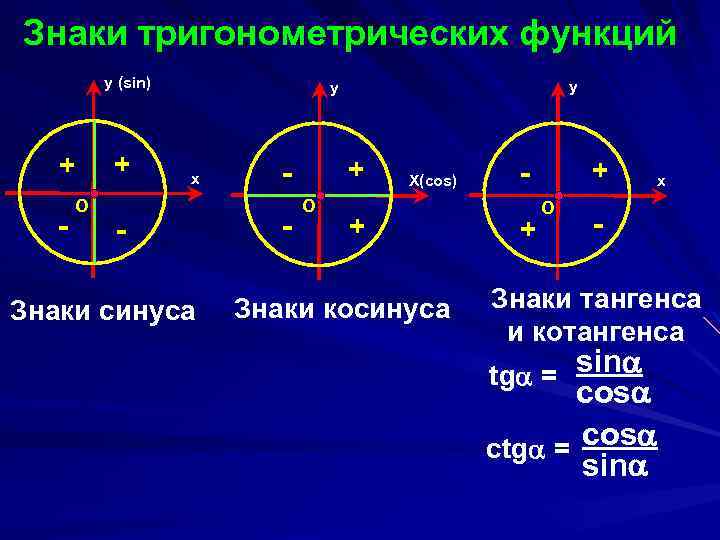Знаки тригонометрических функций y (sin) + - O + y y х - Знаки синуса + - O Х(cos) + Знаки косинуса + + O х - Знаки тангенса и котангенса tg = sin cos ctg = cos sin

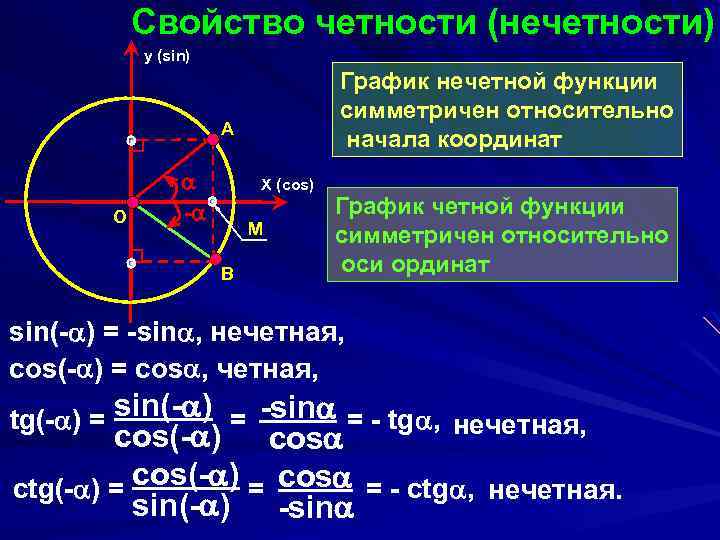Свойство четности (нечетности) y (sin) График нечетной функции симметричен относительно начала координат А O - X (cos) М В График четной функции симметричен относительно оси ординат sin(- ) = -sin , нечетная, cos(- ) = cos , четная, tg(- ) = sin(- ) = -sin = - tg , нечетная, cos(- ) cos ctg(- ) = cos = - ctg , нечетная. sin(- ) -sin

1. Соотношения между тригонометрическими функциями одного и того же аргумента y (sin) sin 2 + cos 2 = 1, А O х у X (cos) М sin , ctg = cos , tg = sin cos

1. Соотношения между тригонометрическими функциями одного и того же аргумента sin 2 + cos 2 = 1 : cos 2 0 sin 2 + cos 2 = 1 : sin 2 0

Формулы приведения Тригонометрические функции углов вида , , 3 , 2 , где - острый угол, 2 2 могут быть выражены через функции угла с помощью формул, которые называются формулами приведения. 1. Для углов и 2 название исходной функции сохраняется, для углов 2 , 3 название исходной функции меняется: 2 синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс. 2. Знак функции определяется, используя тригонометрическую окружность.

Формулы приведения sin( + ) = - sin , y (sin) cos( + ) = - cos , А N + O В X (cos) М 1 tg( + ) = tg , ctg( + ) = ctg ;

Формулы приведения sin( - ) = sin , y (sin) В - N cos( - ) = - cos , А O X (cos) М 1 tg( - ) = - tg , ctg( - ) = - ctg ;

Формулы приведения sin(2 + ) = sin , cos(2 + ) = cos , y (sin) А 2 O X (cos) М 1 + tg(2 + ) = tg , ctg(2 + ) = ctg ; sin(2 k+ ) = sin , k Z, cos(2 k+ ) = cos , k Z, tg(2 k+ ) = tg , k Z, ctg(2 k+ ) = ctg , k Z;

Формулы приведения sin(2 - ) = - sin , y (sin) cos(2 - ) = cos , А 2 - O М X (cos) 1 В tg(2 - ) = - tg , ctg(2 - ) = - ctg ;

Формулы приведения y (sin) В N + 2 O А X (cos) М 1 sin( 2 + ) = cos , cos( 2 + ) = - sin , tg( 2 + ) = - ctg , + ctg( 2 ) = - tg ;

Формулы приведения sin( 2 - ) = cos , y (sin) В N - 2 O cos( 2 - ) = sin , А X (cos) М 1 tg( 2 - ) = ctg , ctg( 2 - ) = tg ;

Формулы приведения sin( 2 + ) = - cos , 3 y (sin) 3 + 2 O А X (cos) М 1 N cos( 2 + ) = sin , 3 tg( 2 + ) = - ctg , 3 ctg( 2 + ) = - tg ; 3 В

Формулы приведения y (sin) 3 - 2 А O X (cos) М 1 N В sin( 2 - ) = - cos , 3 cos( 2 - ) = - sin , 3 tg( 2 - ) = ctg , 3 ctg( 3 - ) = tg ; 2

2. Формулы сложения и вычитания аргументов тригонометрических функций y (sin) P (cos ; sin ) O P (cos ; sin ) X (cos) 1 cos( - ) = cos • cos + sin • sin

cos( + ) = cos • cos - sin • sin( + ) = sin • cos + cos • sin( - ) = sin • cos - cos • sin

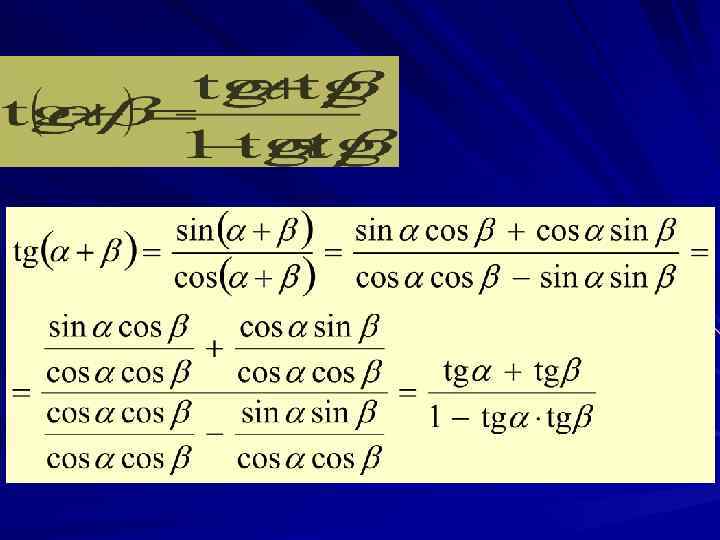
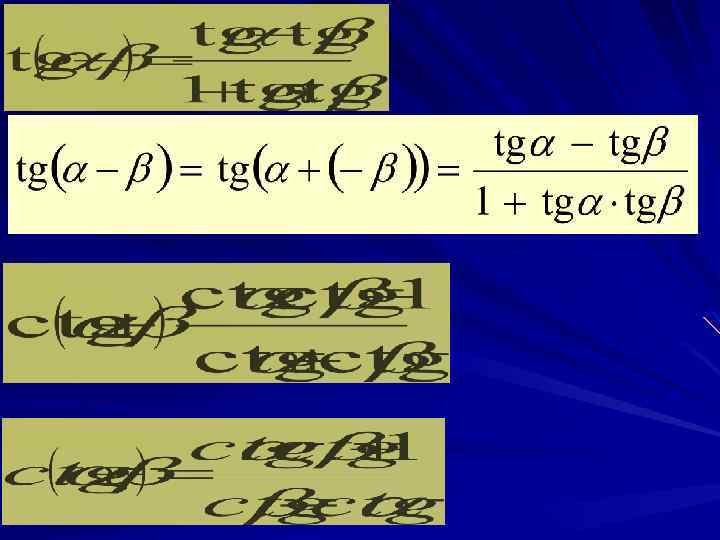
3. Формулы двойных и тройных углов sin 2 = 2 sin cos sin 2 = sin( + ) = sin cos + cos sin = 2 sin cos 2 = cos 2 - sin 2 = 2 cos 2 - 1 = 1 - 2 sin 2 cos 2 = cos( + ) = cos - sin = = cos 2 - sin 2 = cos 2 - (1 – cos 2 ) = 2 cos 2 - 1 = 2(1 – sin 2 ) – 1 = 1 – 2 sin 2

sin 3 = 3 sin - 4 sin 3 = sin( + 2 ) = sin cos 2 + cos sin 2 = = sin (1 - 2 sin 2 ) + cos 2 sin cos = = sin - 2 sin 3 + 2 cos 2 sin = sin - 2 sin 3 + + 2(1 – sin 2 )sin = sin - 2 sin 3 + 2 sin - 2 sin 3 = = 3 sin - 4 sin 3 cos 3 = 4 cos 3 - 3 cos 3 = cos( + 2 ) = cos 2 - sin 2 = = cos (2 cos 2 - 1) - sin 2 sin cos = = 2 cos 3 - cos - 2 sin 2 cos = 2 cos 3 - cos - 2(1 – cos 2 )cos = 2 cos 3 - cos - 2 cos + 2 cos 3 = = 4 cos 3 - 3 cos

4. Преобразование в произведение сумм sin , cos

5. Формулы половинного аргумента

6. Формулы универсальной подстановки

7. Преобразование произведений в суммы или разности

8. Преобразование выражений acos + bsin путем введения вспомогательного угла

Утверждение доказано