Треугольник Типы треугольника Если все углы треугольника

Треугольник.

Типы треугольника. Если все углы треугольника острые, то треугольник называется остроугольным; Если один из углов треугольника тупой(больше 90°), то треугольник называется тупоугольным; Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают. Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.

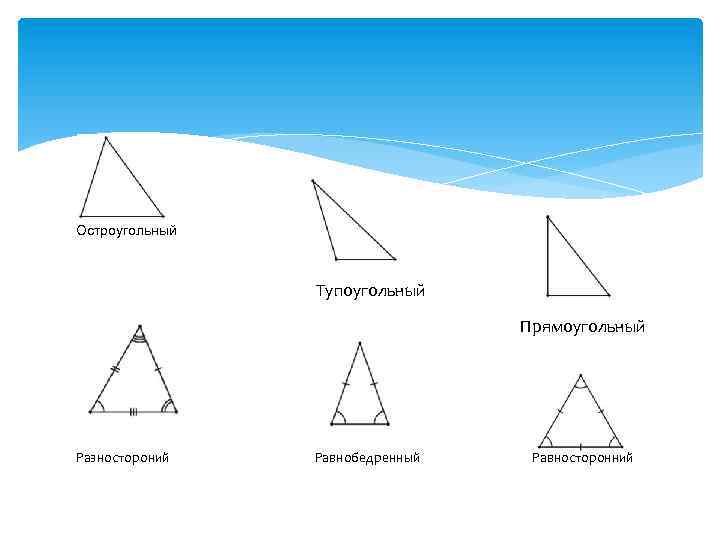Остроугольный Тупоугольный Прямоугольный Разностороний Равнобедренный Равносторонний

Признаки равенства треугольников.

Признак 1 Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Доказательство: Пусть Δ ABC и таковы, что (рис. 4. 2. 1). В соответствии с аксиомой 4. 1 существует равный данному с вершиной в точке с вершиной лежащей на луче и вершиной в той же полуплоскости относительно прямой где лежит вершина (рис. 4. 2. 2). Так как по условию, то на основании аксиомы 1. 5 точки и совпадают (рис. 4. 2. 3). Так как то луч совпадает с лучом (рис. 4. 2. 4). Так как то на основании аксиомы 2. 5 вершина совпадает с вершиной (рис. 4. 2. 5). Тогда совпадает с и, значит, равен Δ ABC. Теорема доказана. Рис. 4. 2. 2 Рис. 4. 2. 3 Рис. 4. 2. 4 Рис. 4. 2. 5 Рис. 4. 2. 1

Признак 2 Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Пусть Δ ABC и таковы, что По аксиоме 4. 1 существует равный Δ ABC, с вершиной на луче и с вершиной в той же полуплоскости, где и вершина Так как то вершина совпадает с вершиной Так как и то луч совпадает с лучом а луч совпадает с лучом Отсюда следует, что вершина совпадает с вершиной Итак, совпадает с треугольником а значит, равен Δ ABC. Теорема доказана. (рис. 4. 2. 6). Рис. 4. 2. 6

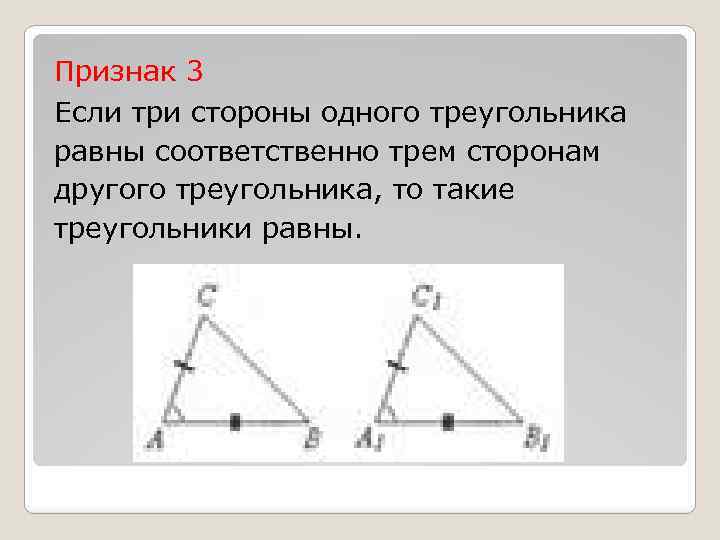Признак 3 Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.

Бермудский треугольник На сайте появилась долгожданная статья Вадима Черноброва о Бермудском треугольнике - подробное описание этой аномальной зоны и связанные с ней гипотезы и истории. А начиналось всё в 1945 году, 60 лет назад. . . Бермудский треугольник - легендарная область Атлантического океана между Пуэрто-Рико, Флоридой и Бермудскими островами, в которой, согласно мнению многих исследователей, происходит множество необъяснимых явлений. Действительно, здесь довольно часто находили дрейфующие суда как с мертвыми экипажами, так и без них. Зафиксированы также бесследные исчезновения самолетов и судов, выход из строя навигационных приборов, радиопередатчиков, часов и т. д. Английский исследователь Лоуренс Д. Куше собрал и проанализировал в хронологическом порядке более 50 случаев исчезновения судов и самолетов в этом районе и пришел к выводу, что легенда о "треугольнике" - не более чем искусственно сфабрикованная мистификация, которая я вилась результатом небрежно проведенных исследований, а затем была доработана авторами, увлекающимися сенсациями. Этой же точки зрения придерживался советский академик Л. М. Бреховских и многие другие исследователи. В пользу такой "официальной" точки зрения можно добавить, что в действительности катастроф в "страшном" месте происходит не так уж и много, через этот район Атлантики проходит огромное количество авиа- и морских перевозок.

ГИПОТЕНУЗА И КАТЕТ. Гипотенуза - (греч. ὑποτείνουσα, натянутая) — самая длинная сторона прямоугольного треугольника, противоположная прямому углу. Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов. Например, если длина одного из катетов равна 3 м (квадрат его длины равен 9 м²), а длина другого — 4 м (квадрат его длины равен 16 м²), то сумма их квадратов равна 25 м². Длина гипотенузы в этом случае равна квадратному корню из 25 м², то есть 5 м. Катет — одна из двух сторон прямоугольного треугольника, образующих прямой угол. Название «катет» происходит от греческого káthetos — перпендикуляр], опущенный, отвесный. Название также встречается в архитектуре и означает отвес через средину задка ионической капители. С катетами связаны тригонометрические функции острого угла α. Прямоугольный треугольник и его гипотенуза (h), а также катеты с1 и с2.