Третий закон Ньютона Закон сохранения импульса Движение

Третий закон Ньютона Закон сохранения импульса Движение центра масс Выполнили студенты гр. 0 А 12: Зинатулина С. Р. Карпович Н. И. Лисов В. И. Логунов А. Проверил преподаватель: Ларионов В. В.

понятие массы тела было введено на основе опытов по измерению ускорений двух взаимодействующих тел: массы взаимодействующих тел обратно пропорциональны численным значениям ускорений или Знак «минус» выражает здесь тот опытный факт, что ускорения взаимодействующих тел всегда направлены в противоположные стороны. Согласно второму закону Ньютона, ускорения тел вызваны силами возникающими при взаимодействии тел. Отсюда следует

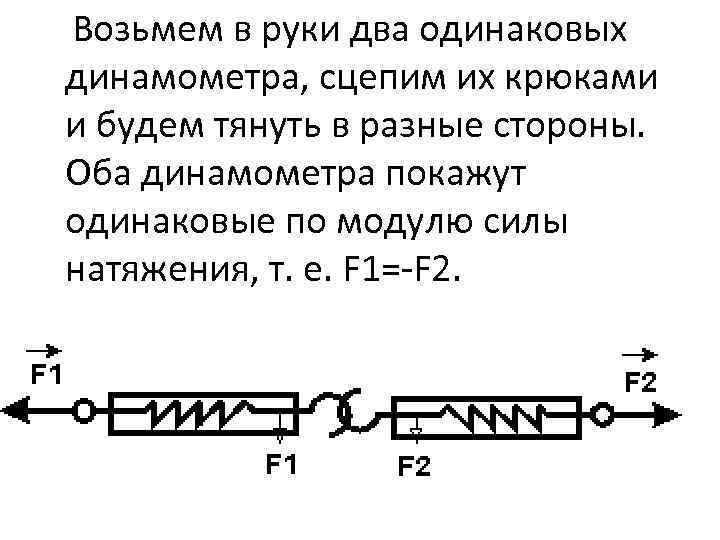Возьмем в руки два одинаковых динамометра, сцепим их крюками и будем тянуть в разные стороны. Оба динамометра покажут одинаковые по модулю силы натяжения, т. е. F 1=-F 2.

Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса.

Закон сохранения импульса Некоторые понятия необходимые для вывода данного закона • Силы взаимодействия между материальными точками механической системы называются внутренними. • Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. • Механическая система тел, на которую не действуют внешние силы, называется замкнутой ( или изолированной)

• Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны и . Пусть -равнодействующие внутренних сил, действующие на каждое из этих тел, а - равнодействующие внешних сил. 2 -й закон Ньютона для каждого из n тел механической системы: Складывая эти уравнения, получим: , или , Где -импульс системы.

Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему В случае отсутствия внешних сил (рассматриваем замкнутую систему) т. е. Последнее выражения является выражением законом сохранения импульса.

Теорема о движении центра масс Центр масс (центр инерции) – это воображаемая точка, характеризующая распределение массы и движение тела или системы частиц как единого целого. • Положение центра масс в классической механике выражается радиус-вектором по формуле: (1) где - масса и радиус-вектор каждой частицы системы, M - масса всей системы материальных точек. • Центр масс в релятивистской механике: где - радиус-вектор центра масс - радиус-вектор каждой частицы системы - полная энергия каждой частицы системы

Получим формулу движения центра масс: • продифференцируем (1) по времени и умножим на М , , , М = m 1 r 1 +m 1 r 2 +… МVс= m 1 v 1 + m 2 v 2 + … , где Vс – скорость центра масс системы. p=М Vс (2) (е) • подставив (2) в формулу dp/dt = ΣFk , получим (е) Мd. Vс /dt = ΣFk или Мас /dt = ΣFk (3) Центр масс системы движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила - геометрической сумме всех внешних сил, действующих на систему. • Проектируя обе части (3) на оси координат, получаем , , (е) Мxc = ΣFkx Муc = ΣFky Мzc = ΣFkz теорему о движении центра масс в координатной форме

Следствия, выражающие закон движения центра масс 1) Если геометрическая сумма, приложенных к системе внешних сил равна нулю (замкнутая система), то центр масс системы находится в покое или движется равномерно или прямолинейно. (е) Если ΣFk , то 2) Если сумма проекций, приложенных к системе внешних сил на некоторую неподвижную ось равна 0, то проекция скорости центра масс системы на эту ось остается постоянной. (е) , , Пусть ΣFkx =0, тогда Мxc =0 и Vсx = const; если Vсx 0 =0, значит xc = const. Система центра масс (С-система) – система отсчета, жестко связанная с центром масс данной системы частиц и перемещающаяся поступательно по отношению к инерциальным системам. Полный импульс системы частиц в С-системе равен нулю.

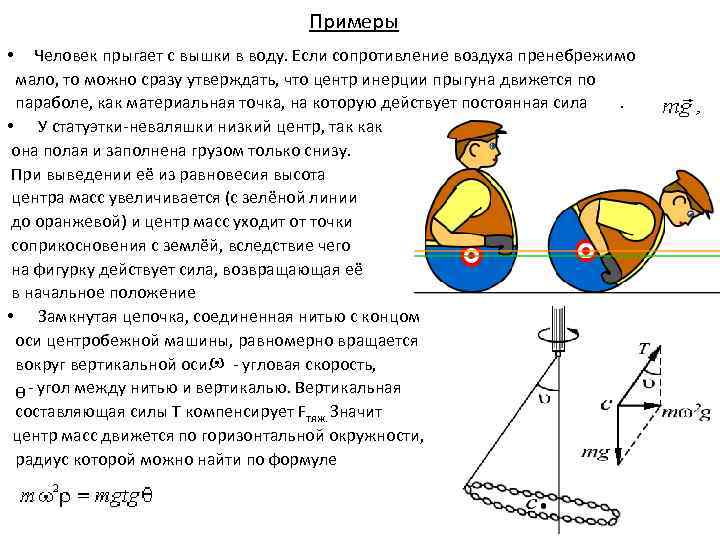Примеры • Человек прыгает с вышки в воду. Если сопротивление воздуха пренебрежимо мало, то можно сразу утверждать, что центр инерции прыгуна движется по параболе, как материальная точка, на которую действует постоянная сила . • У статуэтки-неваляшки низкий центр, так как она полая и заполнена грузом только снизу. При выведении её из равновесия высота центра масс увеличивается (с зелёной линии до оранжевой) и центр масс уходит от точки соприкосновения с землёй, вследствие чего на фигурку действует сила, возвращающая её в начальное положение • Замкнутая цепочка, соединенная нитью с концом оси центробежной машины, равномерно вращается вокруг вертикальной оси. - угловая скорость, - угол между нитью и вертикалью. Вертикальная составляющая силы Т компенсирует Fтяж. Значит центр масс движется по горизонтальной окружности, радиус которой можно найти по формуле