Третий признак равенства треугольников Теорема Если три

Третий признак равенства треугольников.

Теорема: Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны

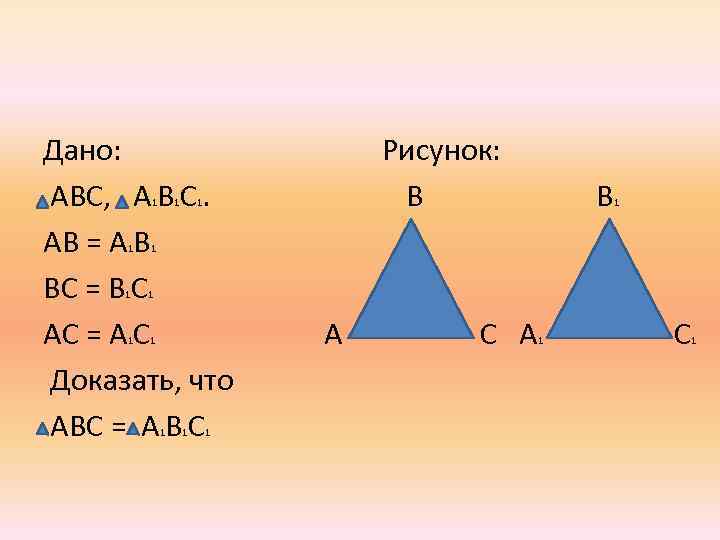Дано: АВС, А В С. АВ = А В ВС = В С АС = А С Доказать, что АВС = А В С 1 1 1 В 1 1 1 1 Рисунок: В 1 1 1 А С А 1 С 1

Доказательство • Наложим АВС на А В С так, чтобы вершины А и А , В и В совместились, а С и С оказались по разные стороны от прямой АВ. • Возможны 3 случая: 1) Луч СС проходит внутри угла А С В. 2) Луч СС совпадает с одной из сторон этого угла. 3) Луч СС проходит вне этого угла. 1 1 1 1

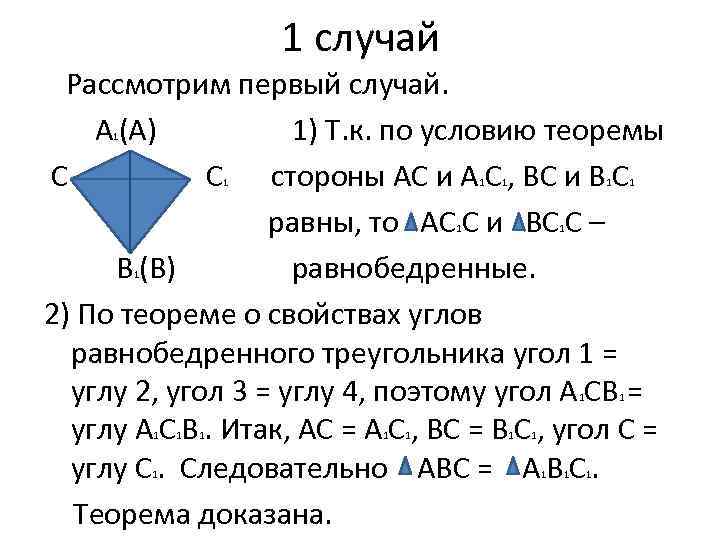1 случай Рассмотрим первый случай. A (A) 1) Т. к. по условию теоремы C C стороны АС и А С , ВС и В С равны, то АС С и ВС С – B (B) равнобедренные. 2) По теореме о свойствах углов равнобедренного треугольника угол 1 = углу 2, угол 3 = углу 4, поэтому угол А СВ = углу А С В. Итак, АС = А С , ВС = В С , угол С = углу С. Следовательно АВС = А В С. Теорема доказана. 1 1 1 1 1 1

2 случай Рассмотрим второй случай. А (А) 1) Т. к. АС = А С , АСС равнобедренный. С С 2) По свойству равнобедренных В (В) треугольников, углы при основании равны, значит угол АСВ = углу А С В 3) АС = А С. АВ – общая сторона. Угол АСВ = углу А С В Следовательно АВС = А В С. Теорема доказана. 1 1 1

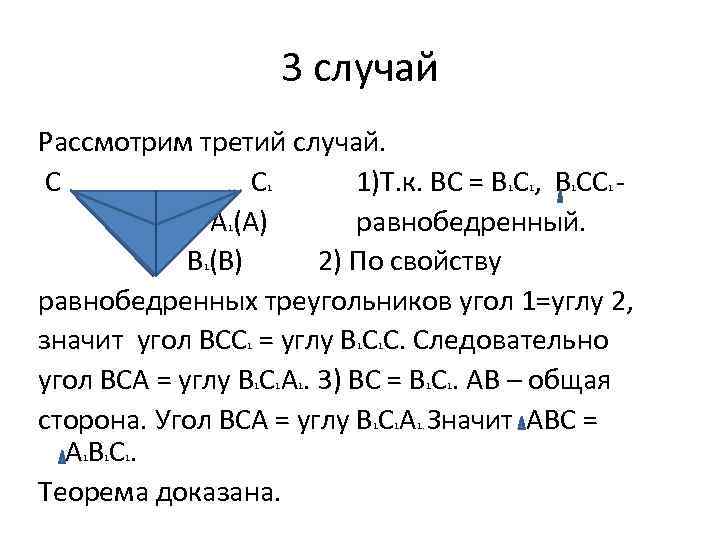3 случай Рассмотрим третий случай. С С 1)Т. к. ВС = В С , В СС А 1 А А (А) равнобедренный. В (В) 2) По свойству равнобедренных треугольников угол 1=углу 2, значит угол ВСС = углу В С С. Следовательно угол ВСА = углу В С А. 3) ВС = В С. АВ – общая сторона. Угол ВСА = углу В С А Значит АВС = АВС. Теорема доказана. 1 1 1 1 1