
Tree дерево

• Binary Trees • A binary tree is an abstract data type defining a finite set of elements. The set is either empty or is partitioned into three subsets. The first subset contains a single element called the root of the tree. • A binary tree is a tree in which each node is the parent of at most two other nodes is known as a binary tree. • In a binary tree, there are never more than two branches descending from a node. • The other two subsets are themselves binary trees, called the left and right sub-trees of the original tree.
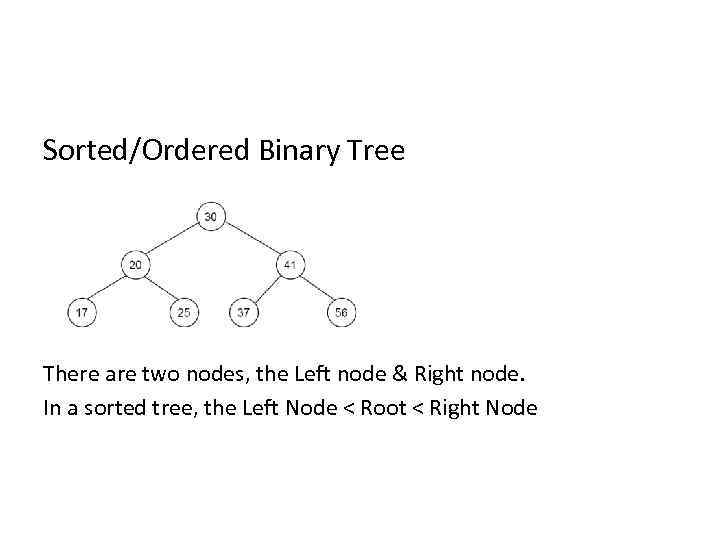
Sorted/Ordered Binary Tree There are two nodes, the Left node & Right node. In a sorted tree, the Left Node < Root < Right Node

Create a binary tree for the following data input: 5, 2, 6, 8, 4, 1, 9, 7, 3 Find the root, leaf and the left sub tree

Traversal of a binary tree means to visit each node of the tree in some order. Usually, the visit means do something with the node, e. g. print its data value. There are three principle ways of traversing a binary tree: 1. Pre-order traversal 2. In-order traversal 3. Post-order traversal These traversals can be specified recursively. The recursive definition states: a tree is either empty or consists of 1. A root 2. A left sub-tree 3. A right- sub-tree.

Preorder Traversal Preorder If tree empty do nothing Otherwise Visit the root node (generally output this) Traverse to left subtree Traverse to right subtree And outputs the following: F, B, A, D, C, E, G, I, H
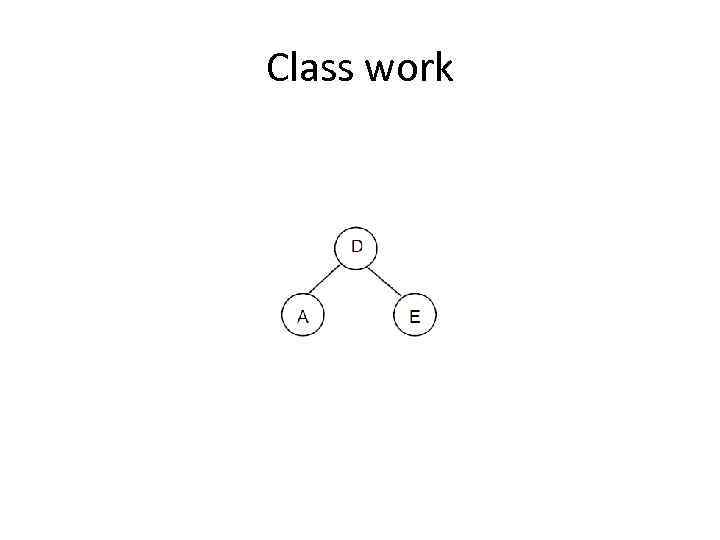
Class work
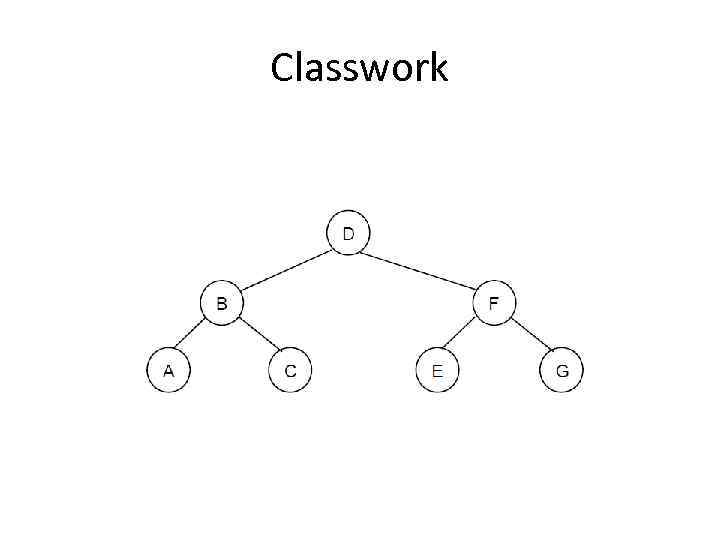
Classwork
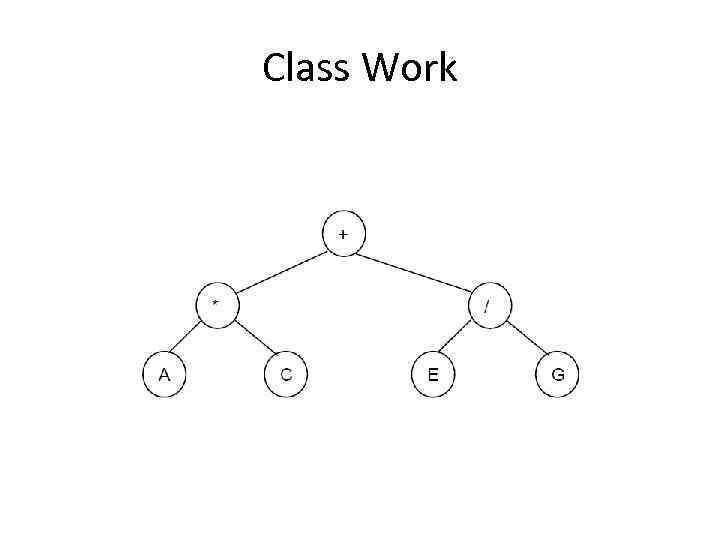
Class Work
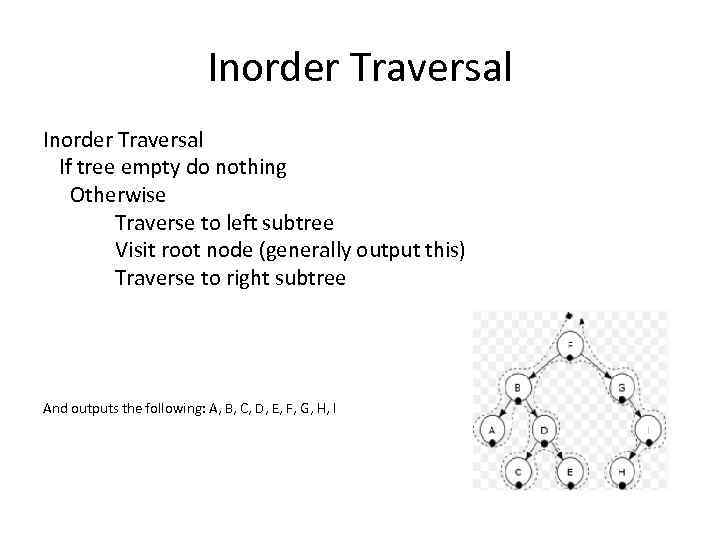
Inorder Traversal If tree empty do nothing Otherwise Traverse to left subtree Visit root node (generally output this) Traverse to right subtree And outputs the following: A, B, C, D, E, F, G, H, I
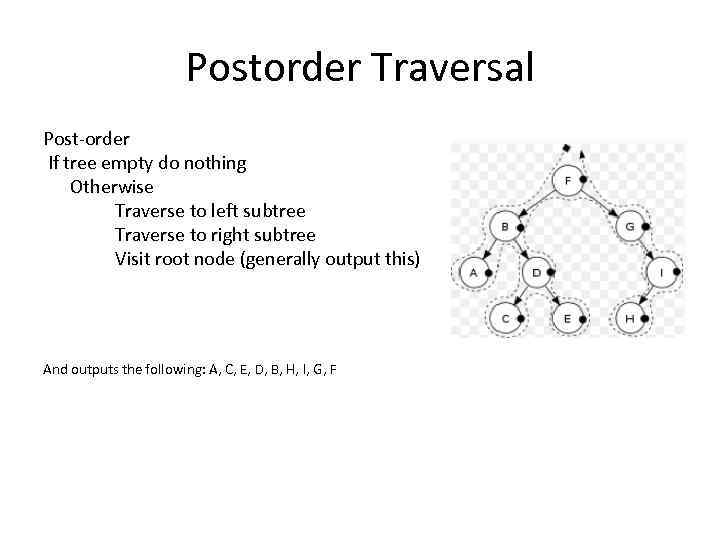
Postorder Traversal Post-order If tree empty do nothing Otherwise Traverse to left subtree Traverse to right subtree Visit root node (generally output this) And outputs the following: A, C, E, D, B, H, I, G, F

Exercises Using the following binary tree: what would be the outputs for: • Pre-order traversal • In-order traversal • Post-order traversal • • Answer : Pre-order traversal: 7, 5, 4, 2, 3, 8, 9, 1 In-order traversal: 4, 2, 5, 3, 7, 9, 8, 1 Post-order traversal: 2, 4, 3, 5, 9, 1, 8, 7