 Трапеция
Трапеция
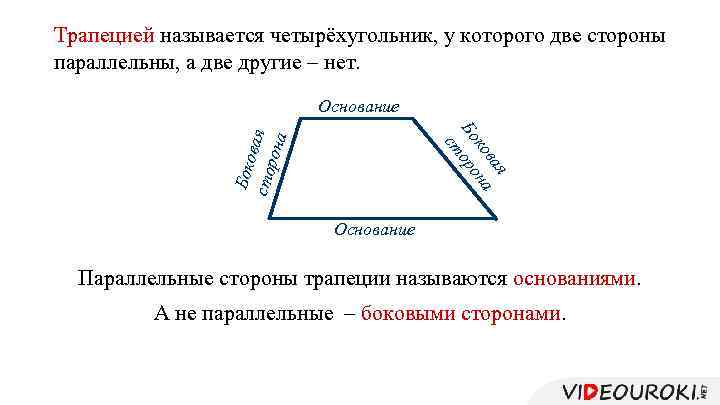 Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие – нет. Основание Боко в сто ая рона я ва ко на Бо оро ст Основание Параллельные стороны трапеции называются основаниями. А не параллельные – боковыми сторонами.
Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие – нет. Основание Боко в сто ая рона я ва ко на Бо оро ст Основание Параллельные стороны трапеции называются основаниями. А не параллельные – боковыми сторонами.
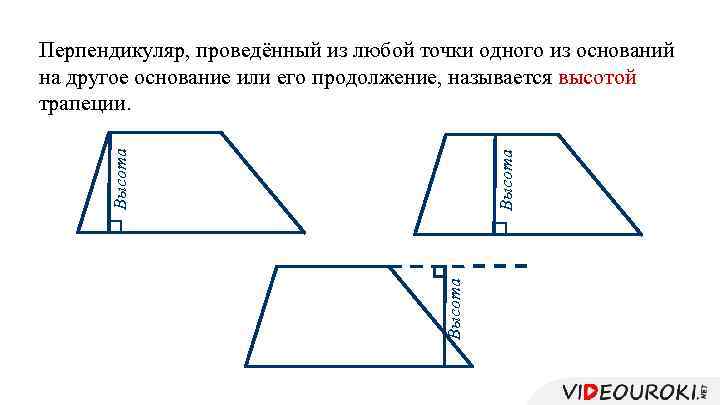 Высота Перпендикуляр, проведённый из любой точки одного из оснований на другое основание или его продолжение, называется высотой трапеции.
Высота Перпендикуляр, проведённый из любой точки одного из оснований на другое основание или его продолжение, называется высотой трапеции.
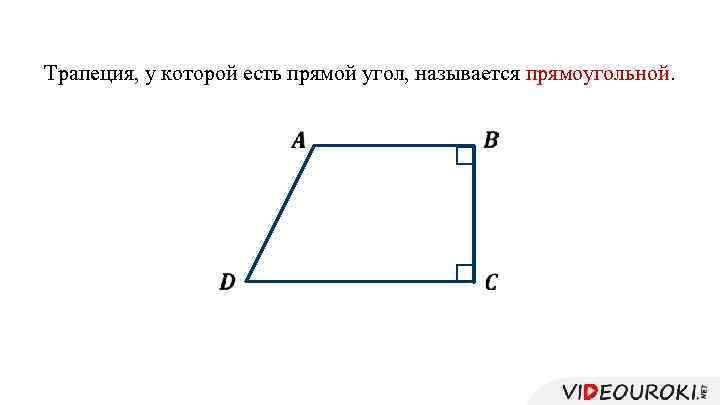 Трапеция, у которой есть прямой угол, называется прямоугольной.
Трапеция, у которой есть прямой угол, называется прямоугольной.
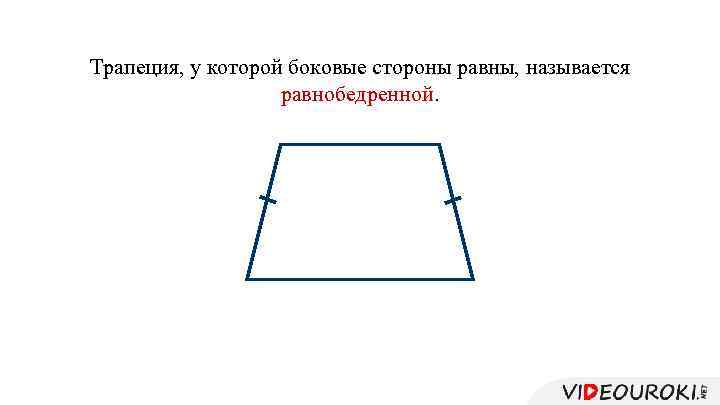 Трапеция, у которой боковые стороны равны, называется равнобедренной.
Трапеция, у которой боковые стороны равны, называется равнобедренной.
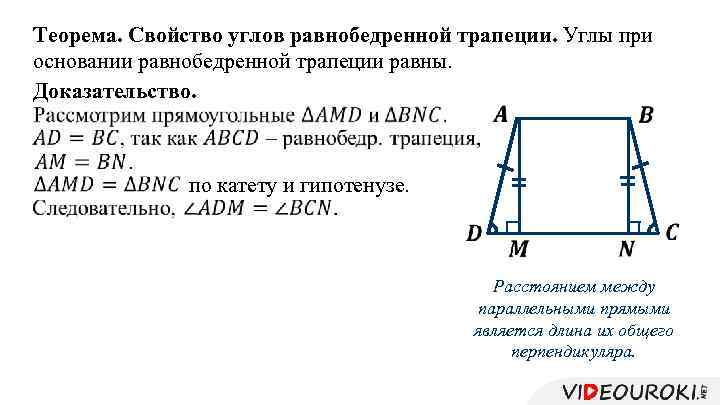 Теорема. Свойство углов равнобедренной трапеции. Углы при основании равнобедренной трапеции равны. Доказательство. по катету и гипотенузе. Расстоянием между параллельными прямыми является длина их общего перпендикуляра.
Теорема. Свойство углов равнобедренной трапеции. Углы при основании равнобедренной трапеции равны. Доказательство. по катету и гипотенузе. Расстоянием между параллельными прямыми является длина их общего перпендикуляра.
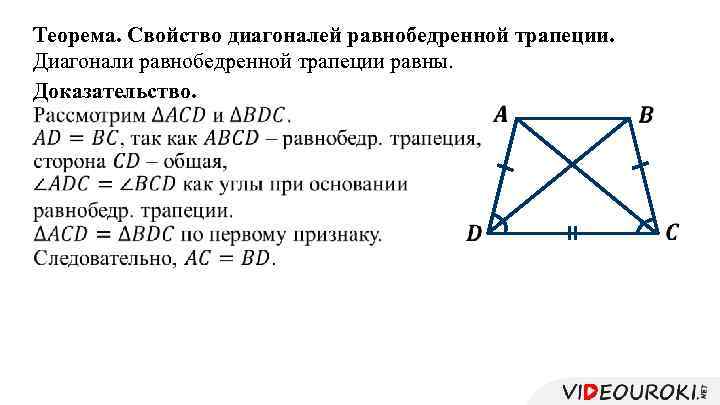 Теорема. Свойство диагоналей равнобедренной трапеции. Диагонали равнобедренной трапеции равны. Доказательство.
Теорема. Свойство диагоналей равнобедренной трапеции. Диагонали равнобедренной трапеции равны. Доказательство.
 Теорема. Признак равнобедренной трапеции. Если у трапеции углы при основании равны, то она равнобедренная. Доказательство. острому углу. по катету и противолежащему
Теорема. Признак равнобедренной трапеции. Если у трапеции углы при основании равны, то она равнобедренная. Доказательство. острому углу. по катету и противолежащему
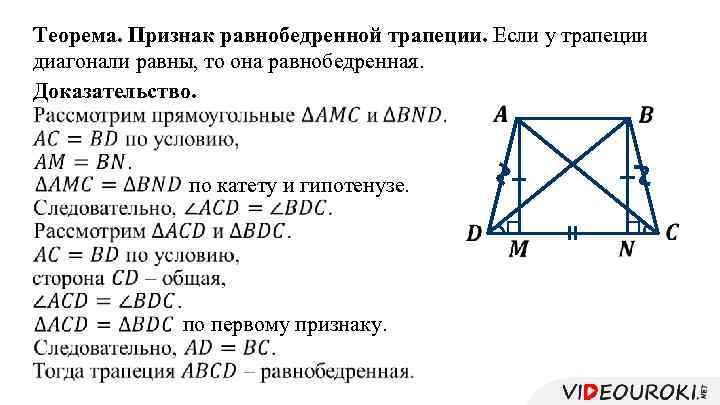 Теорема. Признак равнобедренной трапеции. Если у трапеции диагонали равны, то она равнобедренная. Доказательство. по катету и гипотенузе. по первому признаку.
Теорема. Признак равнобедренной трапеции. Если у трапеции диагонали равны, то она равнобедренная. Доказательство. по катету и гипотенузе. по первому признаку.
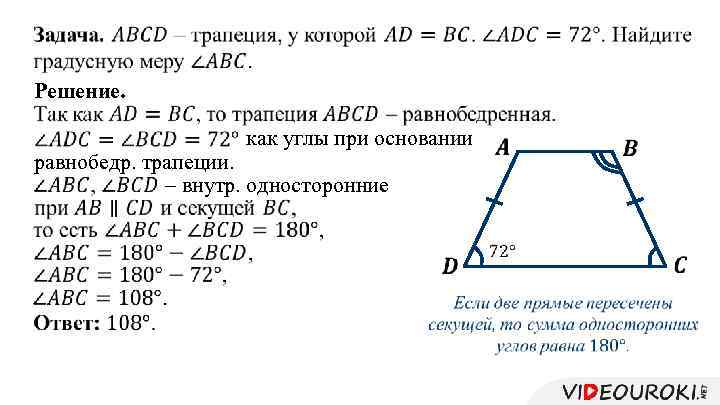 Решение. как углы при основании равнобедр. трапеции. – внутр. односторонние
Решение. как углы при основании равнобедр. трапеции. – внутр. односторонние
 Решение. Углы при основании равнобедренного треугольника равны.
Решение. Углы при основании равнобедренного треугольника равны.