 Трапеция. Основные свойства трапеции. Планиметрия 10 класс
Трапеция. Основные свойства трапеции. Планиметрия 10 класс
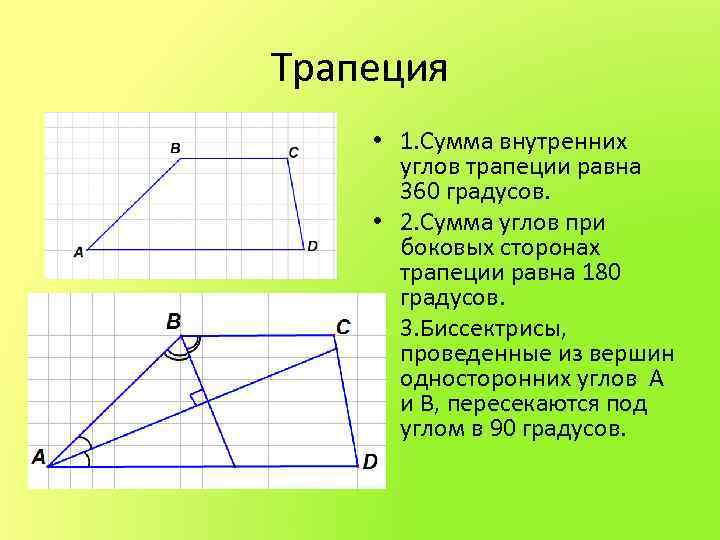 Трапеция • 1. Сумма внутренних углов трапеции равна 360 градусов. • 2. Сумма углов при боковых сторонах трапеции равна 180 градусов. • 3. Биссектрисы, проведенные из вершин односторонних углов А и В, пересекаются под углом в 90 градусов.
Трапеция • 1. Сумма внутренних углов трапеции равна 360 градусов. • 2. Сумма углов при боковых сторонах трапеции равна 180 градусов. • 3. Биссектрисы, проведенные из вершин односторонних углов А и В, пересекаются под углом в 90 градусов.
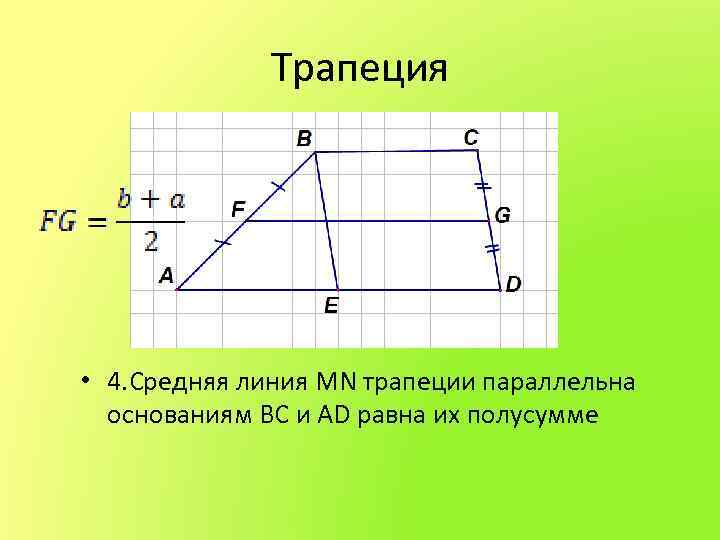 Трапеция • 4. Средняя линия MN трапеции параллельна основаниям BC и AD равна их полусумме
Трапеция • 4. Средняя линия MN трапеции параллельна основаниям BC и AD равна их полусумме
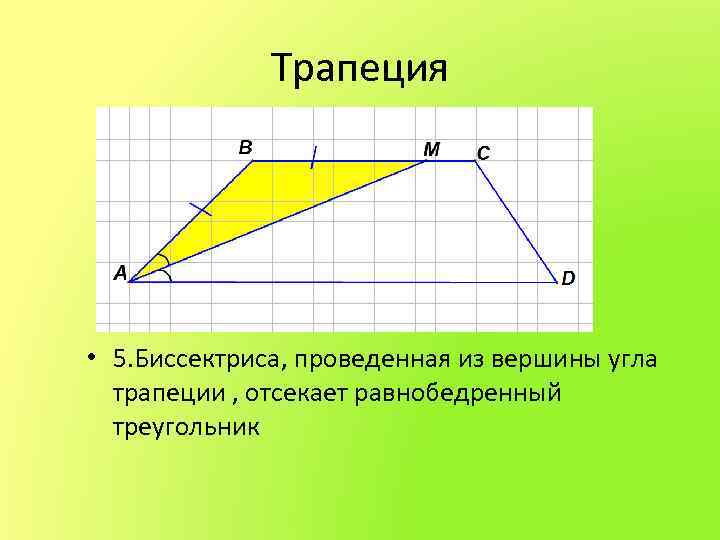 Трапеция • 5. Биссектриса, проведенная из вершины угла трапеции , отсекает равнобедренный треугольник
Трапеция • 5. Биссектриса, проведенная из вершины угла трапеции , отсекает равнобедренный треугольник
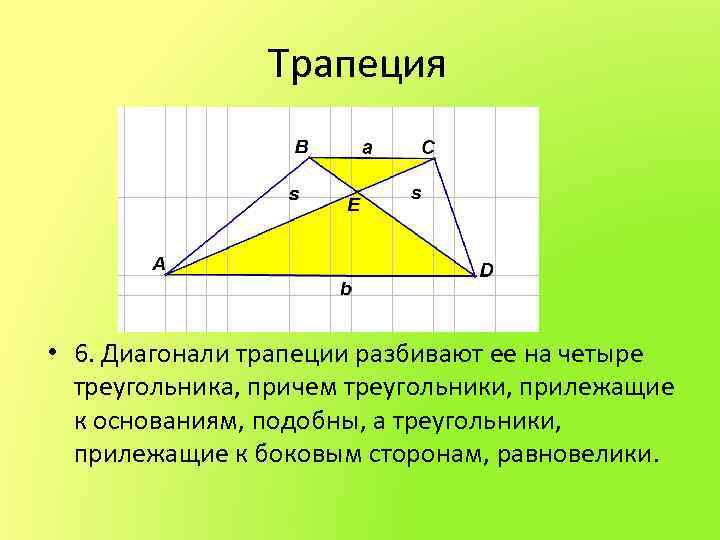 Трапеция • 6. Диагонали трапеции разбивают ее на четыре треугольника, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики.
Трапеция • 6. Диагонали трапеции разбивают ее на четыре треугольника, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики.
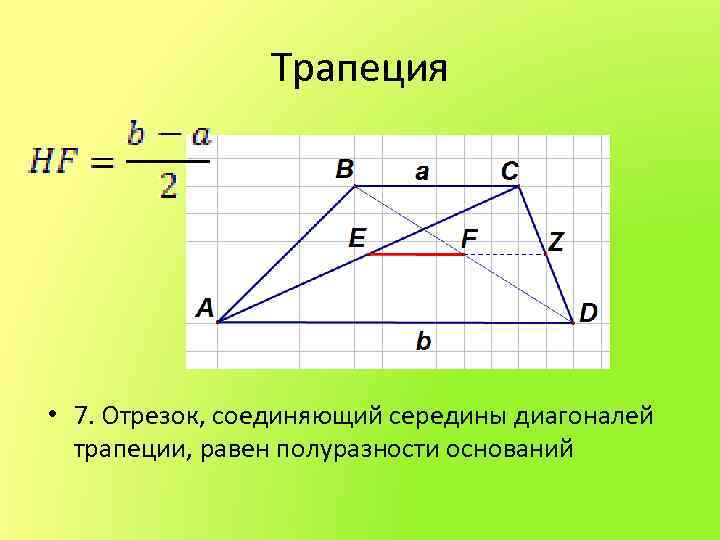 Трапеция • 7. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований
Трапеция • 7. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований
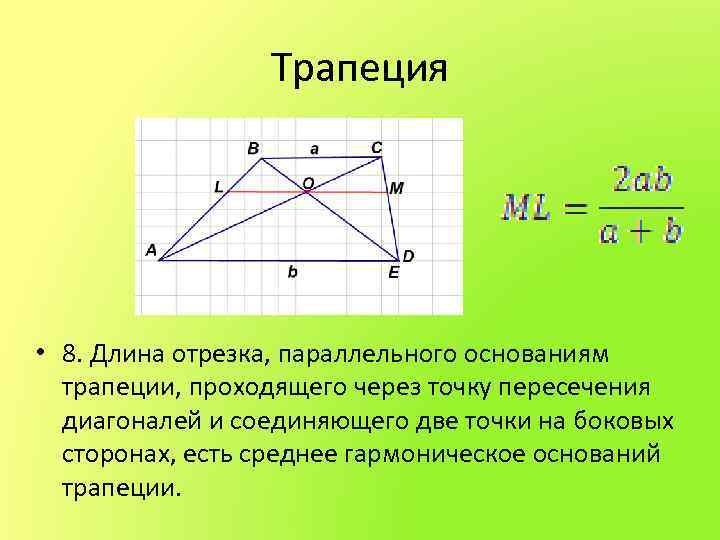 Трапеция • 8. Длина отрезка, параллельного основаниям трапеции, проходящего через точку пересечения диагоналей и соединяющего две точки на боковых сторонах, есть среднее гармоническое оснований трапеции.
Трапеция • 8. Длина отрезка, параллельного основаниям трапеции, проходящего через точку пересечения диагоналей и соединяющего две точки на боковых сторонах, есть среднее гармоническое оснований трапеции.
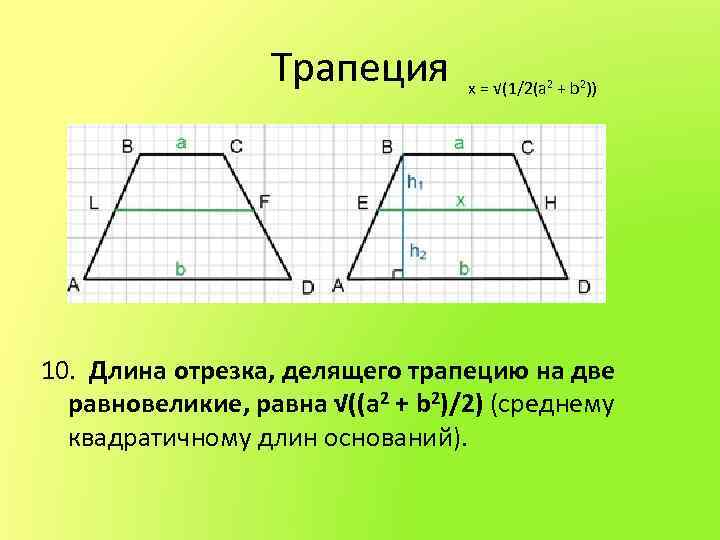 Трапеция х = √(1/2(а 2 + b 2)) 10. Длина отрезка, делящего трапецию на две равновеликие, равна √((а 2 + b 2)/2) (среднему квадратичному длин оснований).
Трапеция х = √(1/2(а 2 + b 2)) 10. Длина отрезка, делящего трапецию на две равновеликие, равна √((а 2 + b 2)/2) (среднему квадратичному длин оснований).
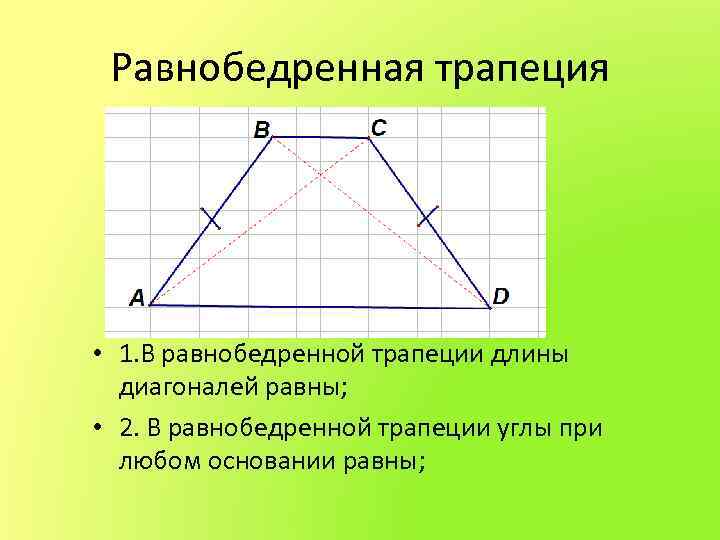 Равнобедренная трапеция • 1. В равнобедренной трапеции длины диагоналей равны; • 2. В равнобедренной трапеции углы при любом основании равны;
Равнобедренная трапеция • 1. В равнобедренной трапеции длины диагоналей равны; • 2. В равнобедренной трапеции углы при любом основании равны;
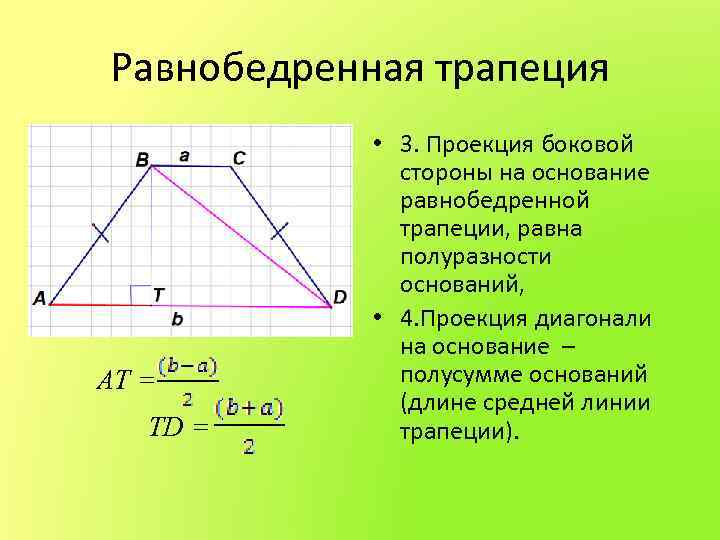 Равнобедренная трапеция АТ = TD = • 3. Проекция боковой стороны на основание равнобедренной трапеции, равна полуразности оснований, • 4. Проекция диагонали на основание – полусумме оснований (длине средней линии трапеции).
Равнобедренная трапеция АТ = TD = • 3. Проекция боковой стороны на основание равнобедренной трапеции, равна полуразности оснований, • 4. Проекция диагонали на основание – полусумме оснований (длине средней линии трапеции).
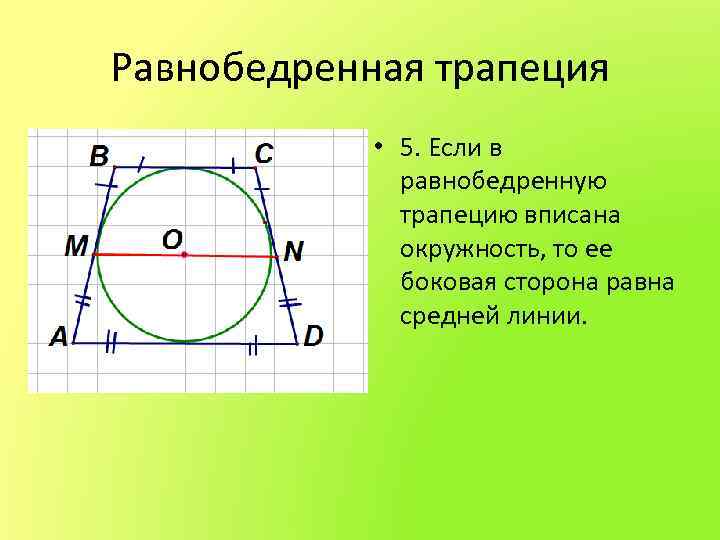 Равнобедренная трапеция • 5. Если в равнобедренную трапецию вписана окружность, то ее боковая сторона равна средней линии.
Равнобедренная трапеция • 5. Если в равнобедренную трапецию вписана окружность, то ее боковая сторона равна средней линии.
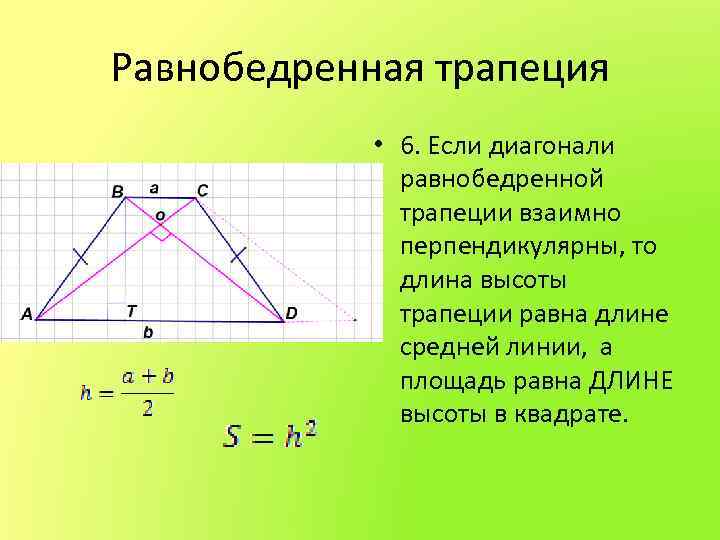 Равнобедренная трапеция • 6. Если диагонали равнобедренной трапеции взаимно перпендикулярны, то длина высоты трапеции равна длине средней линии, а площадь равна ДЛИНЕ высоты в квадрате.
Равнобедренная трапеция • 6. Если диагонали равнобедренной трапеции взаимно перпендикулярны, то длина высоты трапеции равна длине средней линии, а площадь равна ДЛИНЕ высоты в квадрате.
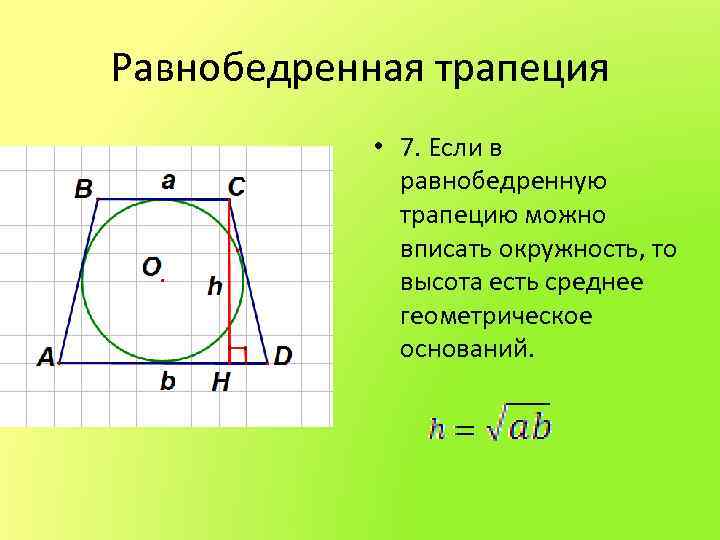 Равнобедренная трапеция • 7. Если в равнобедренную трапецию можно вписать окружность, то высота есть среднее геометрическое оснований.
Равнобедренная трапеция • 7. Если в равнобедренную трапецию можно вписать окружность, то высота есть среднее геометрическое оснований.
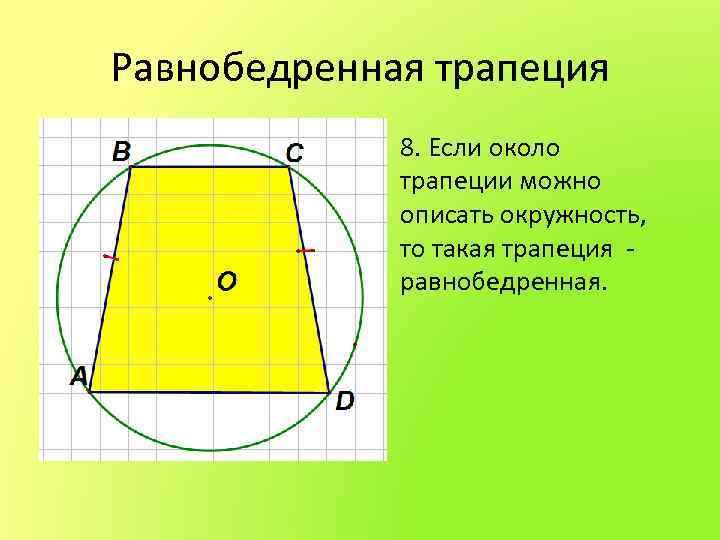 Равнобедренная трапеция • 8. Если около трапеции можно описать окружность, то такая трапеция - равнобедренная.
Равнобедренная трапеция • 8. Если около трапеции можно описать окружность, то такая трапеция - равнобедренная.