9df5ab5f739a1c8763952c22f2ed0a2a.ppt
- Количество слайдов: 66

Transverse dynamics: Orbit Corrections Introduction overview of methods at some (large) accelerators (SLC, HERA, RHIC, LHC) Effects of magnet alignment errors Lattice Diagnostics and R-matrix Reconstruction Online Orbit Fitting as a Diagnostic for Errors Beam-based Alignment of Localized Errors quadrupoles sextupoles accelerating structures Beam Steering Algorithms one-to-one steering global beam-based steering singular valued decomposition “wakefield bumps” dispersion-free steering Summary
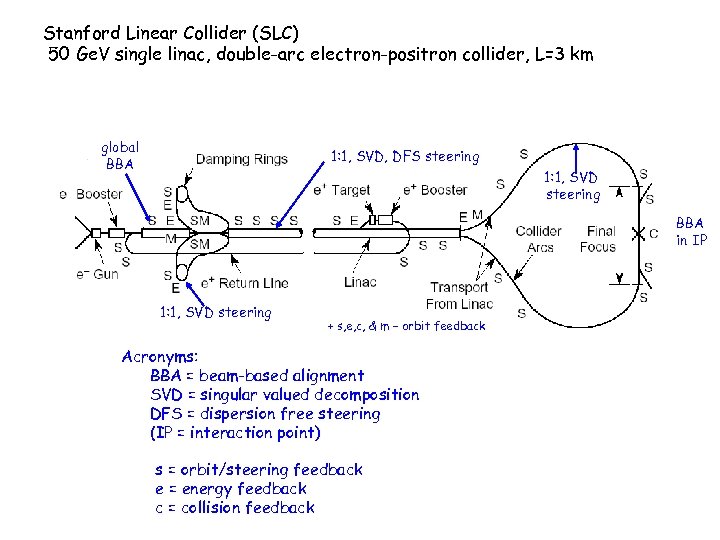
Stanford Linear Collider (SLC) 50 Ge. V single linac, double-arc electron-positron collider, L=3 km global BBA 1: 1, SVD, DFS steering 1: 1, SVD steering BBA in IP 1: 1, SVD steering + s, e, c, & m – orbit feedback Acronyms: BBA = beam-based alignment SVD = singular valued decomposition DFS = dispersion free steering (IP = interaction point) s = orbit/steering feedback e = energy feedback c = collision feedback
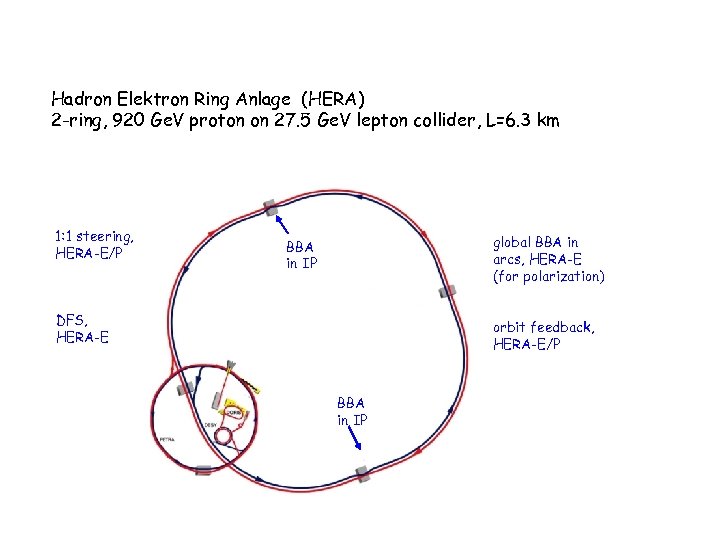
Hadron Elektron Ring Anlage (HERA) 2 -ring, 920 Ge. V proton on 27. 5 Ge. V lepton collider, L=6. 3 km 1: 1 steering, HERA-E/P global BBA in arcs, HERA-E (for polarization) BBA in IP DFS, HERA-E orbit feedback, HERA-E/P BBA in IP
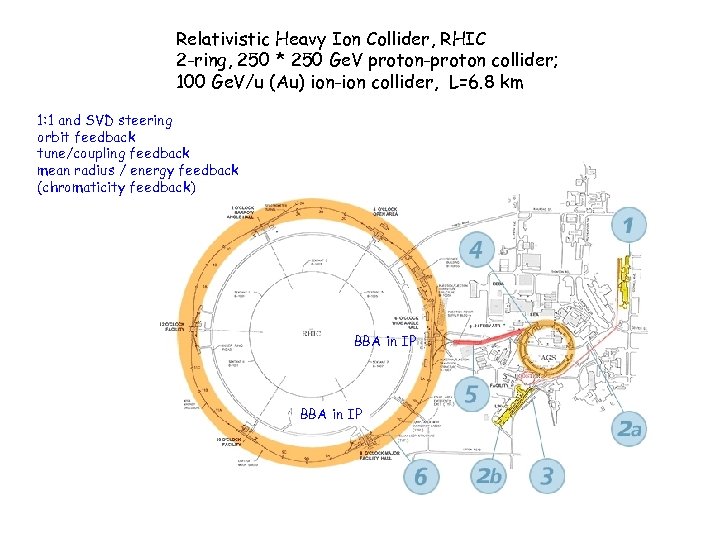
Relativistic Heavy Ion Collider, RHIC 2 -ring, 250 * 250 Ge. V proton-proton collider; 100 Ge. V/u (Au) ion-ion collider, L=6. 8 km 1: 1 and SVD steering orbit feedback tune/coupling feedback mean radius / energy feedback (chromaticity feedback) BBA in IP
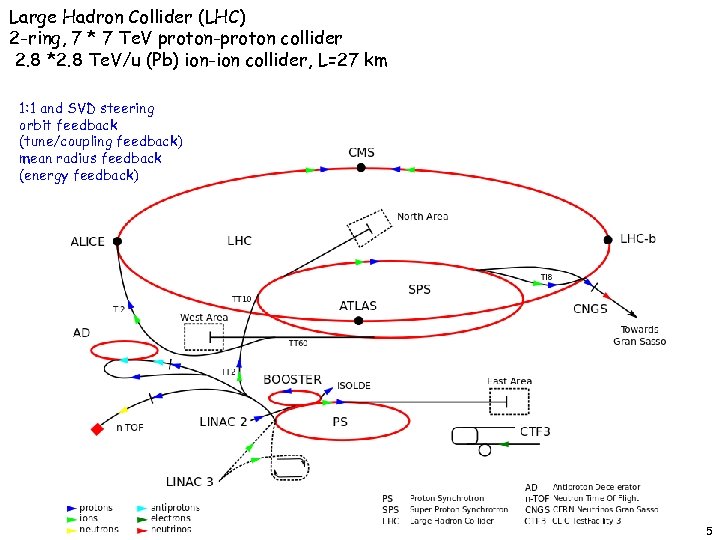
Large Hadron Collider (LHC) 2 -ring, 7 * 7 Te. V proton-proton collider 2. 8 *2. 8 Te. V/u (Pb) ion-ion collider, L=27 km 1: 1 and SVD steering orbit feedback (tune/coupling feedback) mean radius feedback (energy feedback) 5

Effects of magnet alignment errors
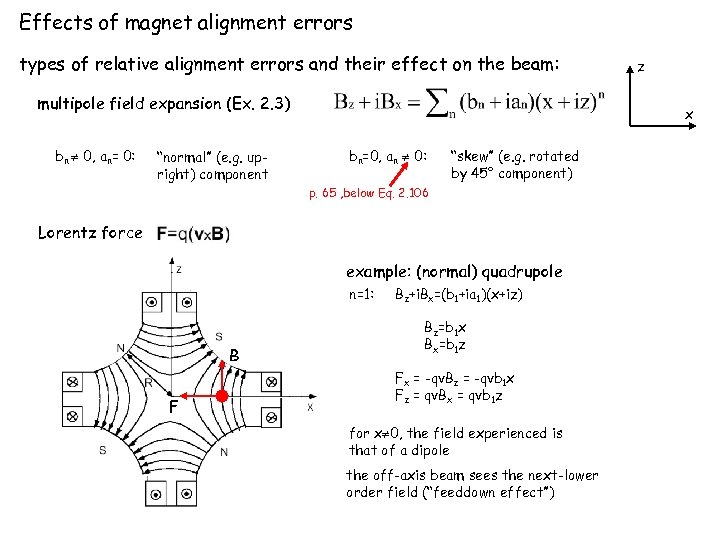
Effects of magnet alignment errors types of relative alignment errors and their effect on the beam: multipole field expansion (Ex. 2. 3) bn 0, an= 0: “normal” (e. g. upright) component x bn=0, an 0: “skew” (e. g. rotated by 45° component) p. 65 , below Eq. 2. 106 Lorentz force example: (normal) quadrupole n=1: B F z Bz+i. Bx=(b 1+ia 1)(x+iz) Bz=b 1 x Bx=b 1 z Fx = -qv. Bz = -qvb 1 x Fz = qv. Bx = qvb 1 z for x 0, the field experienced is that of a dipole the off-axis beam sees the next-lower order field (“feeddown effect”)
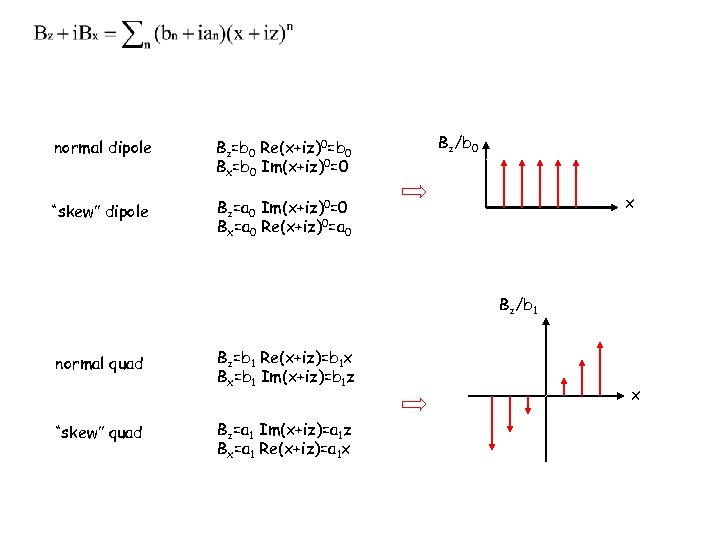
normal dipole Bz=b 0 Re(x+iz)0=b 0 Bx=b 0 Im(x+iz)0=0 “skew” dipole Bz/b 0 Bz=a 0 Im(x+iz)0=0 Bx=a 0 Re(x+iz)0=a 0 x Bz/b 1 normal quad “skew” quad Bz=b 1 Re(x+iz)=b 1 x Bx=b 1 Im(x+iz)=b 1 z Bz=a 1 Im(x+iz)=a 1 z Bx=a 1 Re(x+iz)=a 1 x x
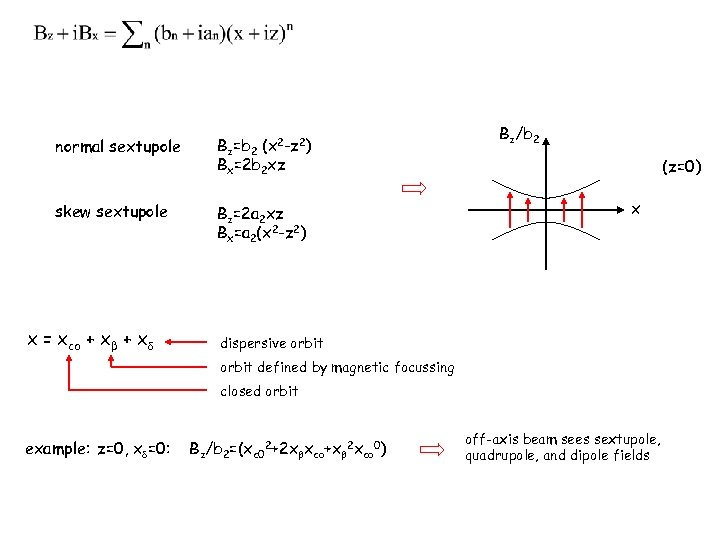
normal sextupole Bz=b 2 (x 2 -z 2) Bx=2 b 2 xz skew sextupole Bz=2 a 2 xz Bx=a 2(x 2 -z 2) x = xco + xβ + x Bz/b 2 (z=0) x dispersive orbit defined by magnetic focussing closed orbit example: z=0, x =0: Bz/b 2=(xc 02+2 x xco+x 2 xco 0) off-axis beam sees sextupole, quadrupole, and dipole fields

In addition to perturbing the design optics, off-axis in quadrupole dipole field: generates dispersion D~1/ρ leads to dispersive emittance growth when ≠ 0 since 1/2 2> x =η and x ~ <x (here x=transverse position offset) leads to beam depolarization when magnetic moment of particle μ experiences a transverse deflecting field B off-axis in sextupole quadrupole and dipole fields: introduces additionally β-beats (gradient errors), vertical dispersion, betatron coupling, … off-axis in accelerating structures wakefield kicks: dilution of projected beam emittance since different particles within the bunch follow different trajectories solutions: alignment (by surveying) steering beam-based alignment feedback (not) covered focus of this lecture covered later causes sampling of nonlinear fields, contributes to emittance growth
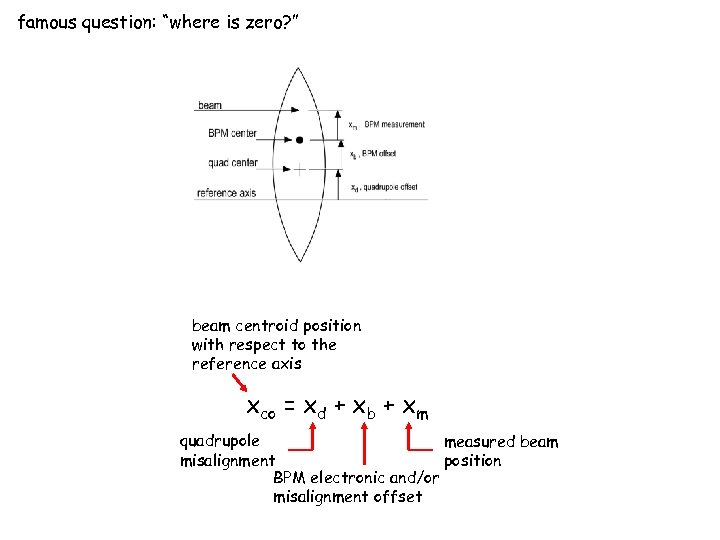
famous question: “where is zero? ” beam centroid position with respect to the reference axis xco = xd + xb + xm quadrupole measured beam misalignment position BPM electronic and/or misalignment offset
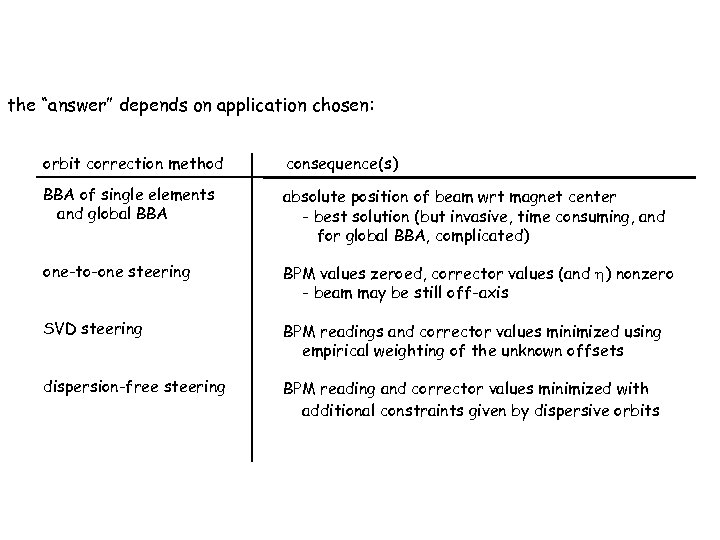
the “answer” depends on application chosen: orbit correction method consequence(s) BBA of single elements and global BBA absolute position of beam wrt magnet center - best solution (but invasive, time consuming, and for global BBA, complicated) one-to-one steering BPM values zeroed, corrector values (and ) nonzero - beam may be still off-axis SVD steering BPM readings and corrector values minimized using empirical weighting of the unknown offsets dispersion-free steering BPM reading and corrector values minimized with additional constraints given by dispersive orbits

Homework #1. The multipole field expansion for a magnet of arbitrary order may be calculated using a useful trick (Laplace’s tree) for avoiding lots of algebra. Consider the example sketched below: order 0 1 1 2 1 (x+y) 3=x 3+3 xy 2+3 x 2 y+y 3 3 1 4 1 4 6 4 1 (etcetera) Make a table showing the position dependence (on x and z) of the vertical (B z) and horizontal (Bx) magnetic fields for upright magnets up to order 4 (octupole magnet). multipole field expansion: #2 Considering a nondispersive orbit (x=xc 0+x , y=yco+y ), show that a beam off-axis in x in a normal sextupole experiences a normal quadrupole field while if off-axis in y, a skew quadrupole field.

Lattice Diagnostics and R-matrix Reconstruction
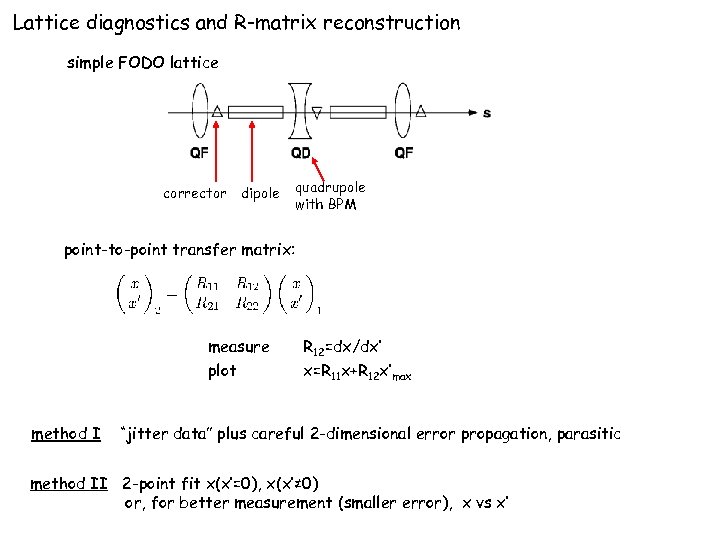
Lattice diagnostics and R-matrix reconstruction simple FODO lattice corrector dipole quadrupole with BPM point-to-point transfer matrix: measure plot method I R 12=dx/dx’ x=R 11 x+R 12 x’max “jitter data” plus careful 2 -dimensional error propagation, parasitic method II 2 -point fit x(x’=0), x(x’≠ 0) or, for better measurement (smaller error), x vs x’
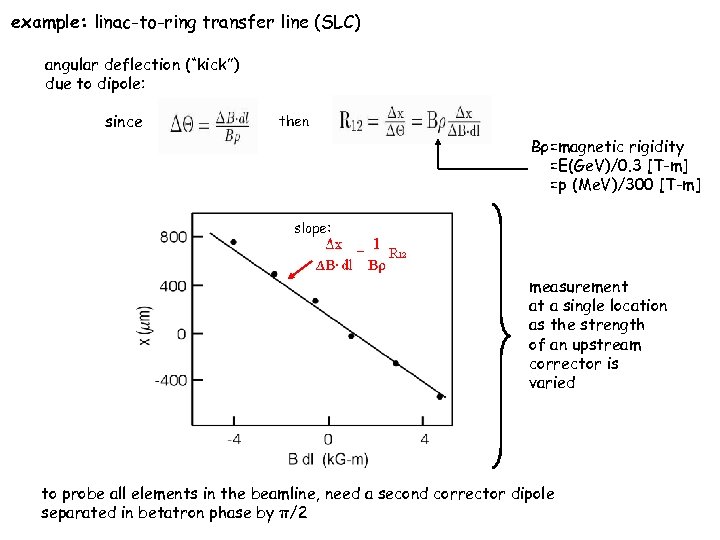
example: linac-to-ring transfer line (SLC) angular deflection (“kick”) due to dipole: since then Bρ=magnetic rigidity =E(Ge. V)/0. 3 [T-m] =p (Me. V)/300 [T-m] slope: measurement at a single location as the strength of an upstream corrector is varied to probe all elements in the beamline, need a second corrector dipole separated in betatron phase by π/2
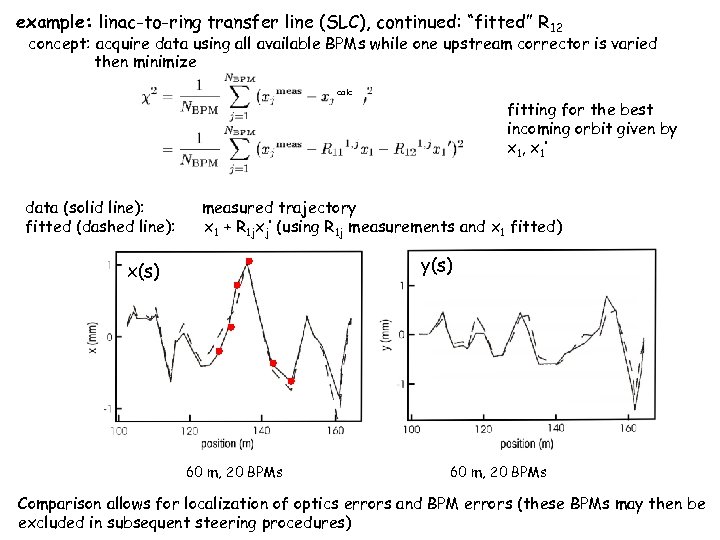
example: linac-to-ring transfer line (SLC), continued: “fitted” R 12 concept: acquire data using all available BPMs while one upstream corrector is varied then minimize calc data (solid line): fitted (dashed line): fitting for the best incoming orbit given by x 1, x 1’ measured trajectory x 1 + R 1 jxj’ (using R 1 j measurements and x 1 fitted) y(s) x(s) 60 m, 20 BPMs Comparison allows for localization of optics errors and BPM errors (these BPMs may then be excluded in subsequent steering procedures)
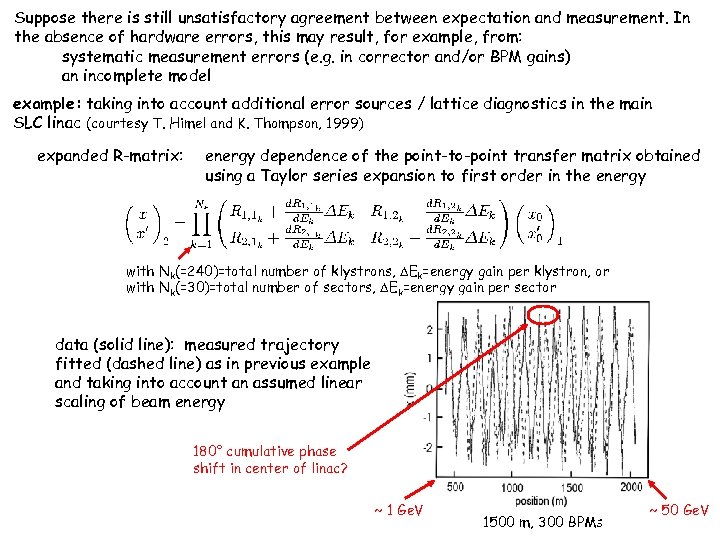
Suppose there is still unsatisfactory agreement between expectation and measurement. In the absence of hardware errors, this may result, for example, from: systematic measurement errors (e. g. in corrector and/or BPM gains) an incomplete model example: taking into account additional error sources / lattice diagnostics in the main SLC linac (courtesy T. Himel and K. Thompson, 1999) expanded R-matrix: energy dependence of the point-to-point transfer matrix obtained using a Taylor series expansion to first order in the energy with Nk(=240)=total number of klystrons, Ek=energy gain per klystron, or with Nk(=30)=total number of sectors, Ek=energy gain per sector data (solid line): measured trajectory fitted (dashed line) as in previous example and taking into account an assumed linear scaling of beam energy 180° cumulative phase shift in center of linac? ~ 1 Ge. V 1500 m, 300 BPMs ~ 50 Ge. V

Possible causes for discrepancy chromatic phase advance in a FODO cell: with (90° FODO cell) if not taken into account, expect a 90° cumulative error with =2. 5%, =30 sectors● 2π/sector unknown energy errors Procedure used for analysis: 1. measure xm(s) versus the applied deflection 2. select a set of Ek’s 3. computed measured 4. iterate for minimum 2
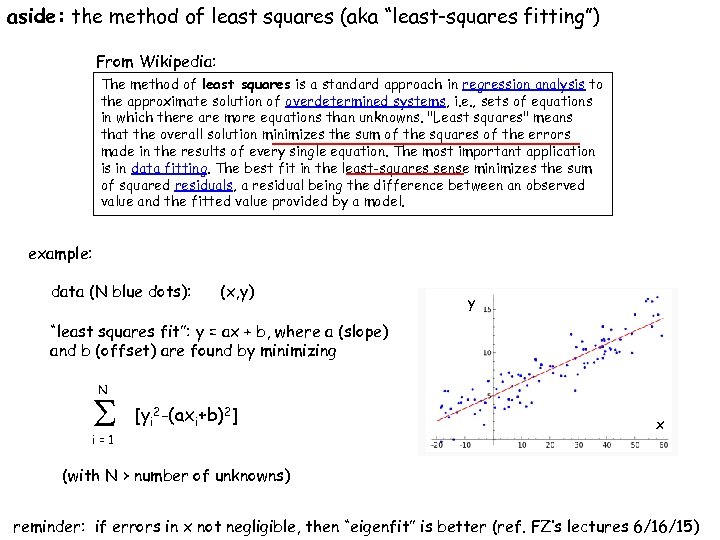
aside: the method of least squares (aka “least-squares fitting”) From Wikipedia: The method of least squares is a standard approach in regression analysis to the approximate solution of overdetermined systems, i. e. , sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in the results of every single equation. The most important application is in data fitting. The best fit in the least-squares sense minimizes the sum of squared residuals, a residual being the difference between an observed value and the fitted value provided by a model. example: data (N blue dots): (x, y) y “least squares fit”: y = ax + b, where a (slope) and b (offset) are found by minimizing N S [yi 2 -(axi+b)2] i=1 x (with N > number of unknowns) reminder: if errors in x not negligible, then “eigenfit” is better (ref. FZ’s lectures 6/16/15)

Back to lattice diagnostics in the SLC linac: equations to be solved: number of unknowns: 30 if Ek = energy gain in each of the 30 sectors 240 if Ek = energy gain per klystron (8 klystrons per sector) number of BPMs (measurements): ~ 300 number of measurements is greater than number of unknowns LS-fit approach ok (note: can limit data set to a few sectors provided number of BPMs still > number of unknowns) solution: 1. measure xm(s) versus the applied deflection 2. select a set of Ek’s 3. compute figure of merit computed measured 4. iterate for minimum figure of merit this is the fit in the least squares sense
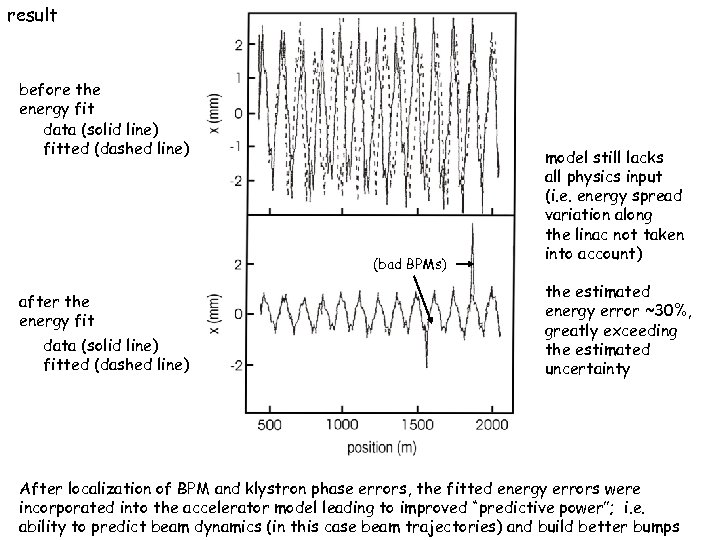
result before the energy fit data (solid line) fitted (dashed line) (bad BPMs) after the energy fit data (solid line) fitted (dashed line) model still lacks all physics input (i. e. energy spread variation along the linac not taken into account) the estimated energy error ~30%, greatly exceeding the estimated uncertainty After localization of BPM and klystron phase errors, the fitted energy errors were incorporated into the accelerator model leading to improved “predictive power”; i. e. ability to predict beam dynamics (in this case beam trajectories) and build better bumps

Online Orbit Fitting as a Diagnostic for Errors

Online Orbit Fitting In essence: - the online model is used to fit the measured beam trajectory in a given plane (cross-plane coupling is neglected) a set of initial coordinates (x, x’) which results in best agreement between the orbit calculated with these initial conditions and the measured orbit is determined. Types of errors that can be found and localized: - component malfunction - deficiencies in the model (including magnet “end-effects” and/or feeddown effects) - anomalies of unknown origin (e. g. stray fields, sensitivities to localized thermal variations) Method Beam position (z=transverse displacement, x or y – here, uncoupled transport) at location s given upstream measurements (z 1, z 1’) (optical functions from model) Construct a difference orbit (as resulting e. g. from some closed orbit distortion) and express as with

Again Select a fit range from the mth to the nth BPM, then For m. ne. n, this gives an overconstrained set of equations with two unknowns, z 1 and z 1’ Define a merit function - measured difference in position at BPM k calculated difference in position at BPM k Minimize merit function, e. g. using least-squares algorithm, to determine z 1 and z 1’ Then the position difference (and angle difference) can be computed at any location along the accelerator Next: examples Remark: application is exact in linear transport lines, but works surprisingly well in circular accelerators (as examples will show)
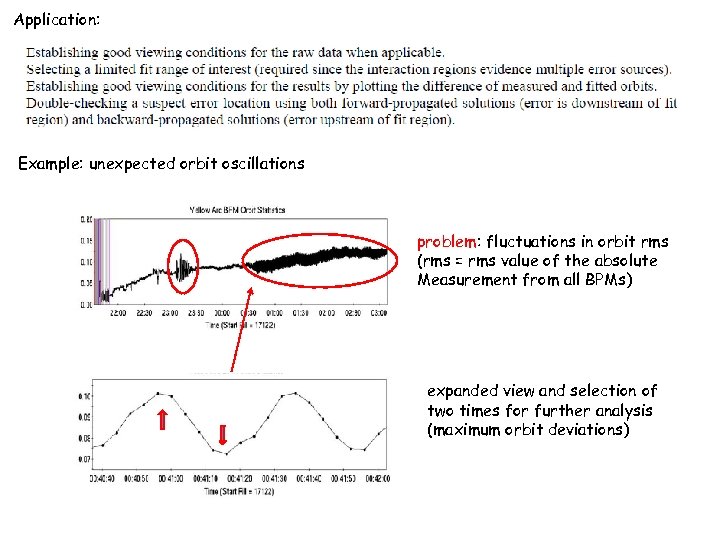
Application: Example: unexpected orbit oscillations problem: fluctuations in orbit rms (rms = rms value of the absolute Measurement from all BPMs) expanded view and selection of two times for further analysis (maximum orbit deviations)
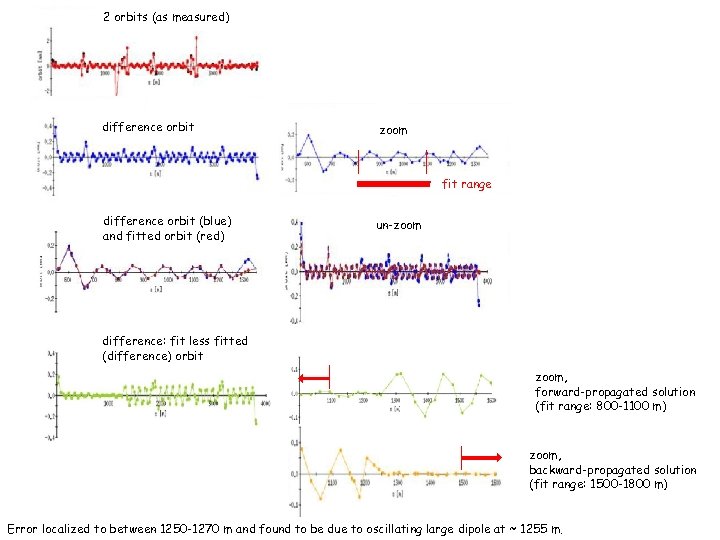
2 orbits (as measured) difference orbit zoom fit range difference orbit (blue) and fitted orbit (red) un-zoom difference: fit less fitted (difference) orbit zoom, forward-propagated solution (fit range: 800 -1100 m) zoom, backward-propagated solution (fit range: 1500 -1800 m) Error localized to between 1250 -1270 m and found to be due to oscillating large dipole at ~ 1255 m.
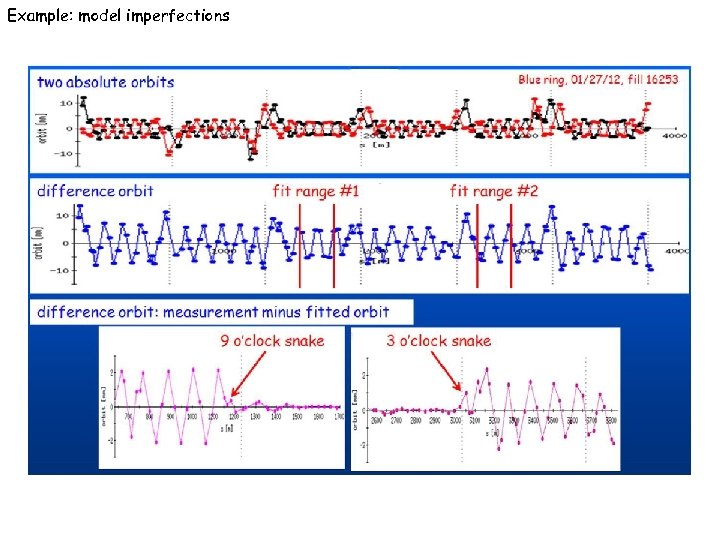
Example: model imperfections

Beam-based Alignment

Beam-based alignment of single elements: quadrupoles typical residual alignment errors after surveying: typical quadrupole alignment tolerances in storage rings (i. e. synchrotron light sources): circular collider IPs (i. e. B-factories, HERA, LHC) linear collider IPs (i. e. NLC, TESLA) ~ (100 -200) μm ~ 10 μm ~ 5 μm < 1 μm Beam-based alignment determines the relative offset between magnet centers and nearby BPMs. If the offsets are sufficiently stable, then orbit correction (steering) can be used to maintain a well-centered orbit.
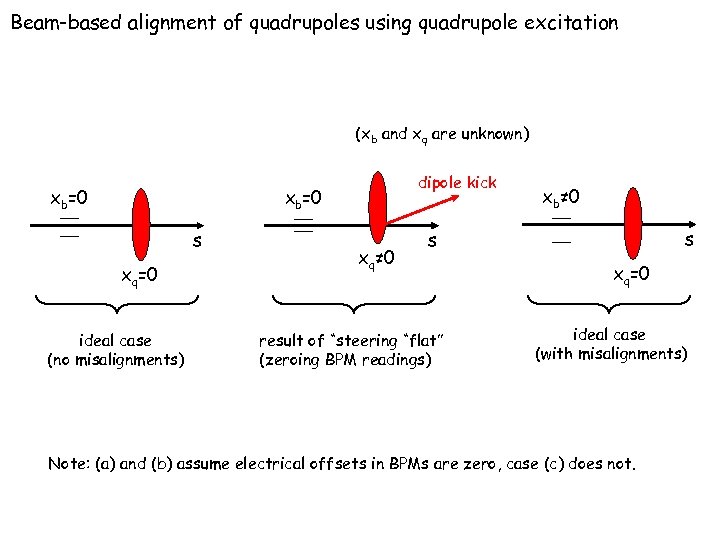
Beam-based alignment of quadrupoles using quadrupole excitation (xb and xq are unknown) xb=0 dipole kick xb=0 s xq=0 ideal case (no misalignments) xq≠ 0 xb≠ 0 s s result of “steering “flat” (zeroing BPM readings) xq=0 ideal case (with misalignments) Note: (a) and (b) assume electrical offsets in BPMs are zero, case (c) does not.
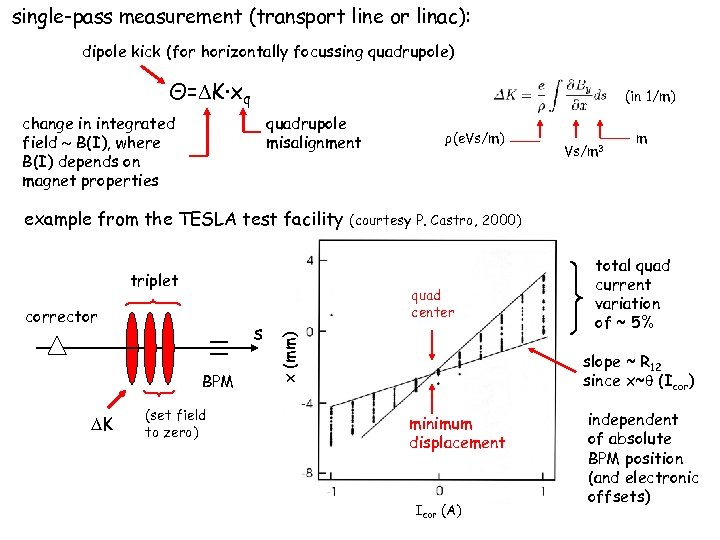
single-pass measurement (transport line or linac): dipole kick (for horizontally focussing quadrupole) Θ= K·xq (in 1/m) change in integrated field B(I), where B(I) depends on magnet properties quadrupole misalignment example from the TESLA test facility triplet s BPM K (set field to zero) Vs/m 3 m (courtesy P. Castro, 2000) quad center x (mm) corrector ρ(e. Vs/m) total quad current variation of ~ 5% slope ~ R 12 since x~ (Icor) minimum displacement Icor (A) independent of absolute BPM position (and electronic offsets)
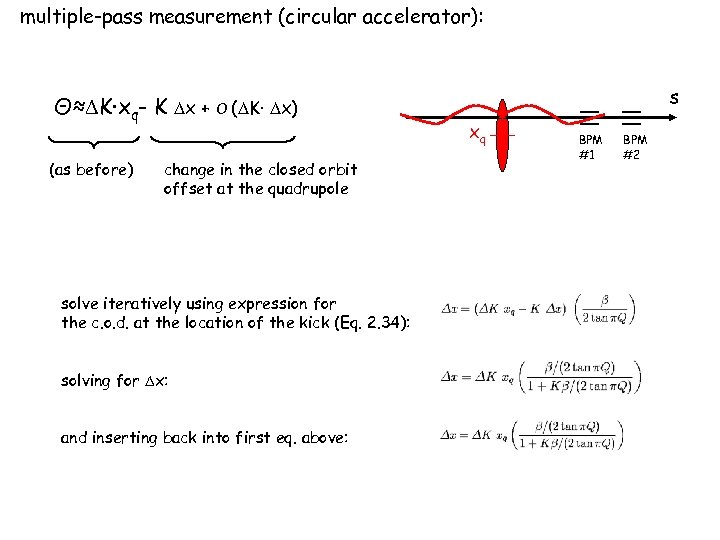
multiple-pass measurement (circular accelerator): Θ≈ K·xq- K x + O ( K· x) (as before) change in the closed orbit offset at the quadrupole solve iteratively using expression for the c. o. d. at the location of the kick (Eq. 2. 34): solving for x: and inserting back into first eq. above: s xq BPM #1 BPM #2
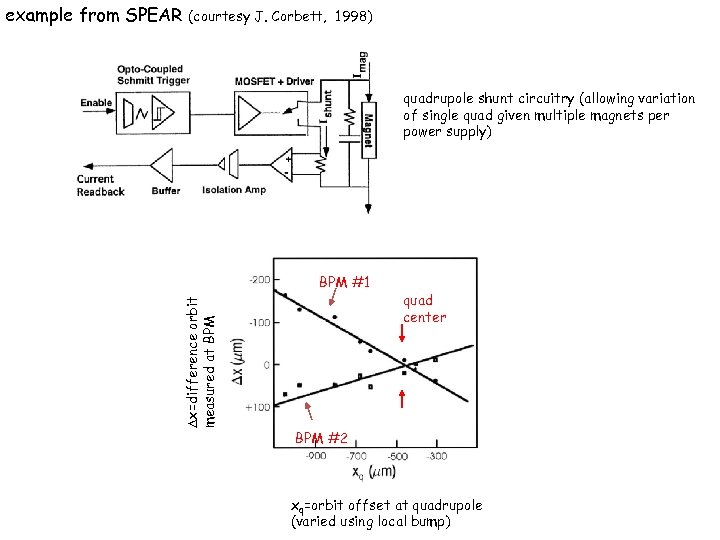
example from SPEAR (courtesy J. Corbett, 1998) quadrupole shunt circuitry (allowing variation of single quad given multiple magnets per power supply) x=difference orbit measured at BPM #1 quad center BPM #2 xq=orbit offset at quadrupole (varied using local bump)
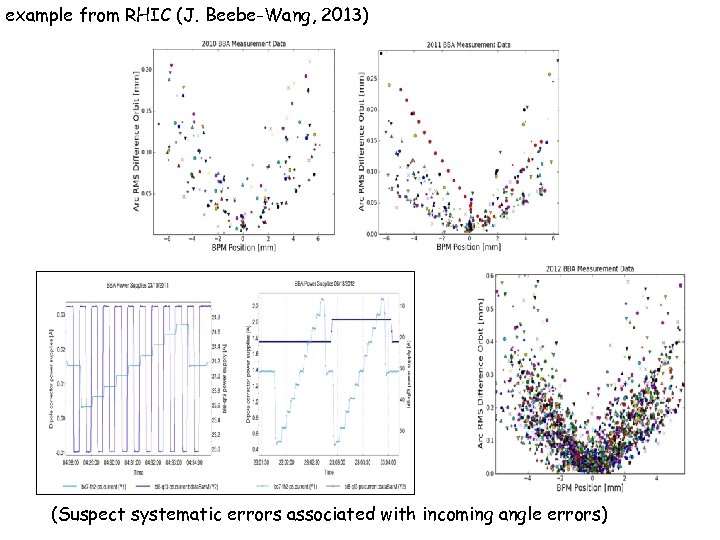
example from RHIC (J. Beebe-Wang, 2013) (Suspect systematic errors associated with incoming angle errors)
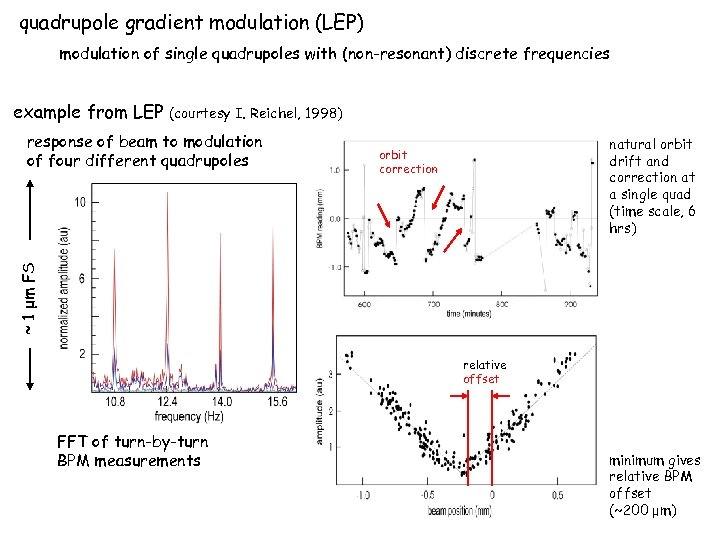
quadrupole gradient modulation (LEP) modulation of single quadrupoles with (non-resonant) discrete frequencies example from LEP (courtesy I. Reichel, 1998) natural orbit drift and correction at a single quad (time scale, 6 hrs) orbit correction ~ 1 μm FS response of beam to modulation of four different quadrupoles relative offset FFT of turn-by-turn BPM measurements orbit variation measured at BPM close to modulated quad using position jitter (time scale short) minimum gives relative BPM offset (~200 μm)

Beam-based alignment of single elements: sextupoles recall (normal sextupole): Θx~Bz=b 2 (x 2 -z 2) Θz~Bx=2 b 2 xz Possible approaches (using sampled quadrupole field): 1. use additional quadrupole trim windings, mounted on the sextupoles, quadrupole-based BBA (KEK) – (assumes coinciding magnetic centers of trim windings and sextupole) 2. measure shift in betatron tune vs sextupole strength (PEP-II, HERA, …): θ x~ ( xβ + xco )2 - ( zβ + zco )2 ~ … + xβxco + … zβzco + … off-axis in x (xco≠ 0) θx~xβ (quadrupole field); similarly in z 3. measure tune separation near the difference resonance vs sextupole strength (NLC): θz ~ … + xβzco + … off-axis in z (zco≠ 0) θz~xβ (skew quadrupole field) need for each sextupole an individual power supply

Possible approaches (using sampled dipole field): 1. using local orbit bumps (KEK, DESY): horizontal sextupole alignment: θx = -0. 5 Ks (xbump-xs)2 θz = -0. 5 Ks (xbump-xs)zs vertical sextupole alignment: θz = Ks (x 0 -xs)(zbump-zs) xs and zs are the sextupole offsets change strength of all sextupoles by Ks measure induced orbit change repeat for different bump amplitudes independent of the number of sextupoles driven by a single power supply x 0 is a preferably large horizontal orbit offset (for enhanced sensitivity)
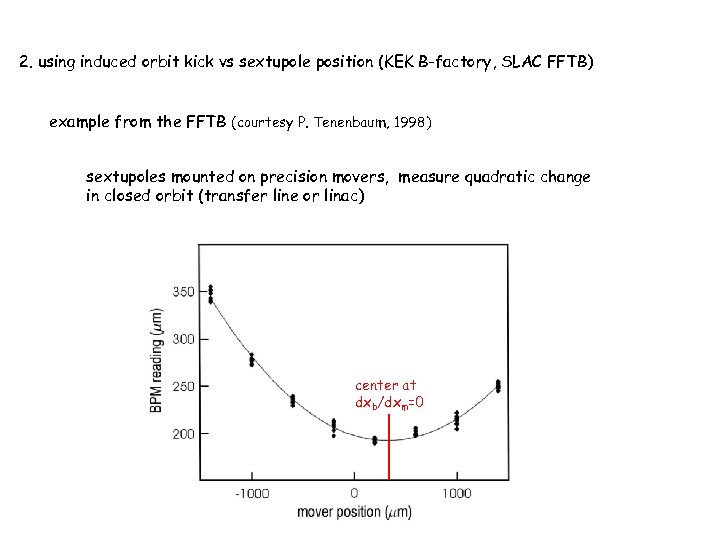
2. using induced orbit kick vs sextupole position (KEK B-factory, SLAC FFTB) example from the FFTB (courtesy P. Tenenbaum, 1998) sextupoles mounted on precision movers, measure quadratic change in closed orbit (transfer line or linac) center at dxb/dxm=0
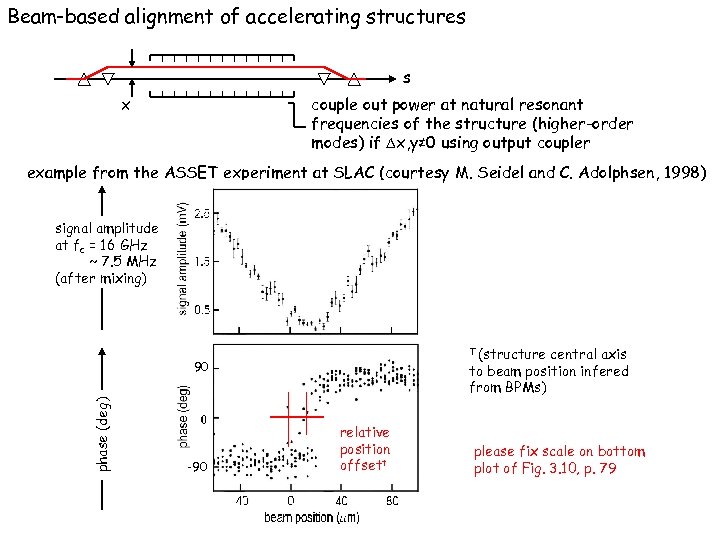
Beam-based alignment of accelerating structures s x couple out power at natural resonant frequencies of the structure (higher-order modes) if x, y≠ 0 using output coupler example from the ASSET experiment at SLAC (courtesy M. Seidel and C. Adolphsen, 1998) signal amplitude at fc = 16 GHz ~ 7. 5 MHz (after mixing) T (structure central axis to beam position infered from BPMs) phase (deg) 90 -90 relative position offsett please fix scale on bottom plot of Fig. 3. 10, p. 79

Homework #3. Design a 2 -corrector “ -bump” (phase advance between correctors is ). a) determine the ratio of the applied kick angles 1/ 2 in terms of the beta functions at the correctors 1 and 2, b) supposing 1= 2, what is the position offset in the middle of the bump (take = 1/2) assuming a 1 mrad applied deflection angle? # 4. Using 4 correctors, determine the coefficients of so-called symmetric (x≠ 0 and x’=0) and asymmetric bumps (x=0 and x’≠ 0) at the middle of the bump assuming a symmetric optic about this point and that =0 there. Hint: evaluate the required kick angles using two correctors and apply symmetry arguments to determine the kick angles at the other correctors. With = 1/2= 2/2, what are the deflections angles required to produce x=1 mm and x’=1 mrad at the symmetry point? symmetric bump: asymmetric bump: s Hint for both exercises: apply linear superposition s
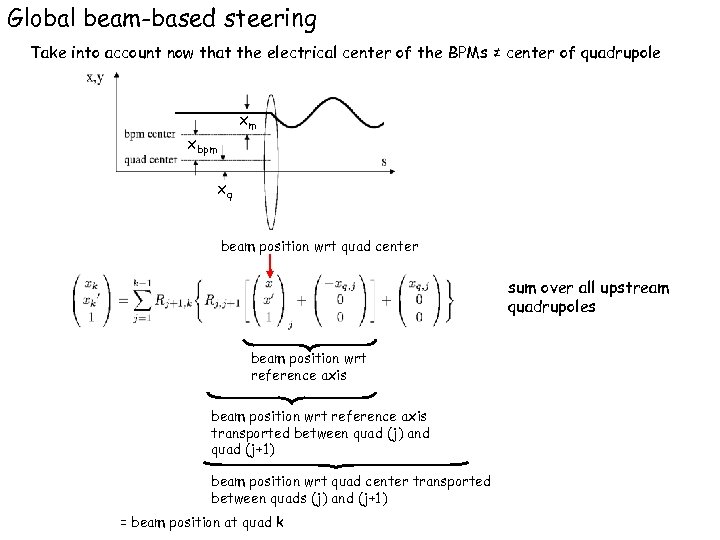
Global beam-based steering Take into account now that the electrical center of the BPMs ≠ center of quadrupole xm xbpm xq beam position wrt quad center sum over all upstream quadrupoles beam position wrt reference axis transported between quad (j) and quad (j+1) beam position wrt quad center transported between quads (j) and (j+1) = beam position at quad k

again rearrange terms sum over upstream quadrupoles function to be minimized: measurements fitting function with unknowns xq, xbpm, and (x 0, x 0’) Since the number of measurements is about ½ the number of unknowns, an independent set of measurements is required. One possibility is to scale the lattice (all quadrupole and corrector strengths) and repeat the measurement.

Beam Steering Algorithms

Beam Steering Algorithms review: so far we have discussed beam-based alignment of single elements which, while accurate, is time consuming and so used most often during early stages of accelerator commissioning and in interaction regions, where single-element alignment tolerances are most critical lattice diagnostics which is often needed prior to being able to implement automated steering algorithms, which may be model-dependent and are significantly less prone to errors if “bad BPMs” are already excluded from the data samples until now (in the discussion of BBA and lattice diagnostics) only the coherent motion of the bunch centroid (center of charge) has been considered Beam steering is applied over long regions of the accelerator and is significantly more time-efficient than BBA of single elements. Note that while the center of charge is measured by the BPMs, the steering algorithms generally do minimize the projected beam emittance. With x = horizontal or vertical, x = xβ + x dispersive orbit defined by magnetic focussing The emittance εx ~ σx 2/β, where σx = <x 2>1/2 = <(xβ + x )2>1/2 closed orbit which contains for example a dispersive term σ =<x 2>1/2= 2< 2>1/2

“One-to-One” steering Beam is steered to zero the transverse displacements measured by the BPMs. The BPMs are typically mounted inside the quadrupoles (where the β-functions are largest). closed bump that would minimize the BPM readings (but would also generate dispersion) Beam position measured at a downstream BPM (denoted by subscript, j): In matrix form with indices i denote each corrector kick m is the total number of BPM measurements n is the total number correctors Solving the matrix equation: or x is the vector containing the BPM measurements Θ is the vector containing the unknown kick angles

Again , the solution is given by Here, θ is an (n 1) matrix [n=number of correctors] M is an (n m) matrix x is an (m 1) matrix [m=number of BPM readings (per plane of interest)] If m>n, the matrix M is overdetermined m=n, the matrix M is square and the solution is simply θ=M-1 x m<n, the matrix M is underdetermined and more measurements are needed (to ensure that the number of unknowns is at least equal to the number of measurements). To constrain the solution in this case, some parameter (e. g. the beam energy) needs to be varied and the measurement repeated (however, the measurement fails to be noninvasive)

minimization procedure: (using linear least-squares algorithm) The solution to the matrix equation minimizing can equivalently be found by fitting function with unknowns Θi (i = number of unknown kicks) measurements (j = number of BPM measurements) i. e. (algebra) i. e. vary the unknowns θi given the BPM measurements xj and the assumed transfer elements Mji so that the relation holds (as closely as possible) (reorganizing terms) This equation, expressed in matrix form, is equivalent to the result from before:

Homework # 5. One-to-One steering a) Consider a transport line with a single BPM. Given a measured transverse displacement of x 1, give an expression for the required kick angle of a single upstream corrector to zero the displacement. The answer may be expressed in terms of the beta functions at the corrector βc and at the BPM βb and of the relative phase advance b- c. b) Consider a transport line with the geometry, lattice functions, and symbol definitions shown below: x correctors BPMs (i) c 1 = π/2 c 2 = π 1 = 3π/2 2 = 2π Plot the required kick angles θ 1 and θ 2 as a function of the measured displacements x 1 and x 2 assuming that the beta functions at the correctors and the BPMs are (for purposes of this illustration) all equal and equal to 5 m. Express the slopes in both graphs numerically. Remark: this example, while easy to solve numerically, is well adapted for extension to more BPMs and correctors if solved using MATLAB. As a then reminder, if (ii) Suppose x 1=x 2=10 mm. Assuming a beam energy of 1 Ge. V and corrector dipole lengths of 6 cm, what are the magnetic fields required to provide the corrections? Reminder: where Bρ =magnetic rigidity = p/c = E (Ge. V)/0. 3 [T-m] s

Singular valued decomposition (SVD) Global orbit correction using the SVD algorithm offers the advantage of reducing not only the rms of the BPM measurements, but also the rms of the applied corrector strengths. Correctors compensating (or “fighting”) one another generate unwanted dispersion. This powerful algorithm may also be used in application to orbit feedback, dispersion-free steering, and in the computation of multiknobs matrix of corrector kick angles, (n 1) matrix Matrix equation to be solved: measured orbit displacements, (m 1) matrix (linear) orbit response matrix, (m n) matrix m=number of BPM readings n=number of correctors If m>n, the matrix A may be decomposed (easily using matlab, for example) U is an (m n) matrix V is an (n n) matrix The column vectors of U and V are orthonormal satisfying (I n is the (n n) identity matrix)

Again, A is an (m n) matrix m=number of BPM readings n=number of correctors m=n: A is square matrix and the solution for the correctors is If none of the wi are zero, the solution is unique (example to follow). If one or more of the wi are zero (degenerate case), there may not be an exact solution. In this case, replace 1/wi by zero which gives still the solution in the least squares sense; i. e |A●θ- x| and |θ|2 are minimized. m<n: Add rows with zeroes to the vectors and matrices in x=Aθ until the A matrix is square and apply the SVD algorithm as just described (again a degenerate case) m>n: SVD solution will agree with the result of the least-square fit
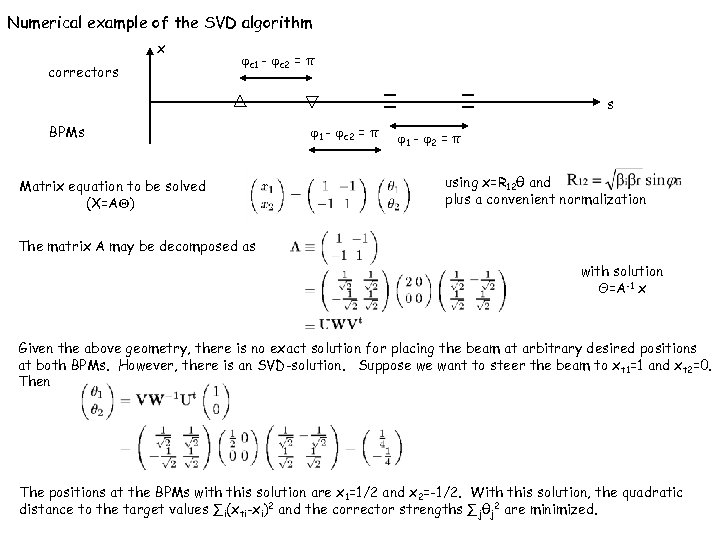
Numerical example of the SVD algorithm x correctors c 1 - c 2 = π s BPMs Matrix equation to be solved (X=AQ) 1 - c 2 = π 1 - 2 = π using x=R 12θ and plus a convenient normalization The matrix A may be decomposed as with solution Θ=A-1 x Given the above geometry, there is no exact solution for placing the beam at arbitrary desired positions at both BPMs. However, there is an SVD-solution. Suppose we want to steer the beam to x t 1=1 and xt 2=0. Then The positions at the BPMs with this solution are x 1=1/2 and x 2=-1/2. With this solution, the quadratic distance to the target values ∑i(xti-xi)2 and the corrector strengths ∑jθj 2 are minimized.
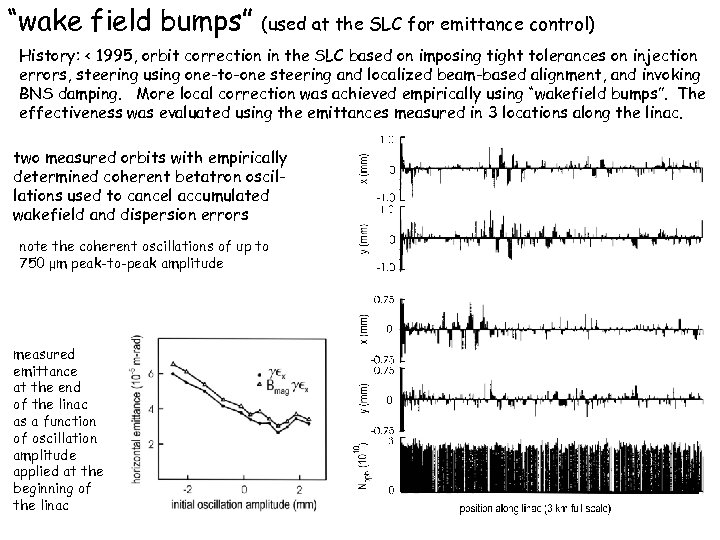
“wake field bumps” (used at the SLC for emittance control) History: < 1995, orbit correction in the SLC based on imposing tight tolerances on injection errors, steering using one-to-one steering and localized beam-based alignment, and invoking BNS damping. More local correction was achieved empirically using “wakefield bumps”. The effectiveness was evaluated using the emittances measured in 3 locations along the linac. two measured orbits with empirically determined coherent betatron oscillations used to cancel accumulated wakefield and dispersion errors note the coherent oscillations of up to 750 μm peak-to-peak amplitude measured emittance at the end of the linac as a function of oscillation amplitude applied at the beginning of the linac
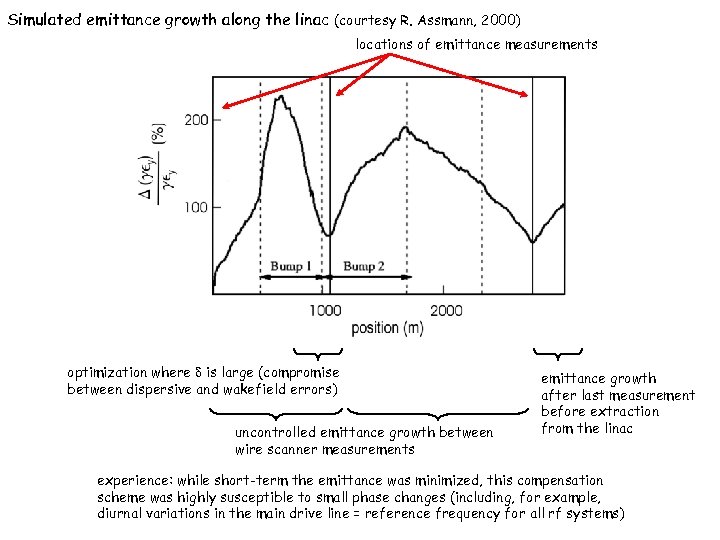
Simulated emittance growth along the linac (courtesy R. Assmann, 2000) locations of emittance measurements optimization where is large (compromise between dispersive and wakefield errors) uncontrolled emittance growth between wire scanner measurements emittance growth after last measurement before extraction from the linac experience: while short-term the emittance was minimized, this compensation scheme was highly susceptible to small phase changes (including, for example, diurnal variations in the main drive line = reference frequency for all rf systems)
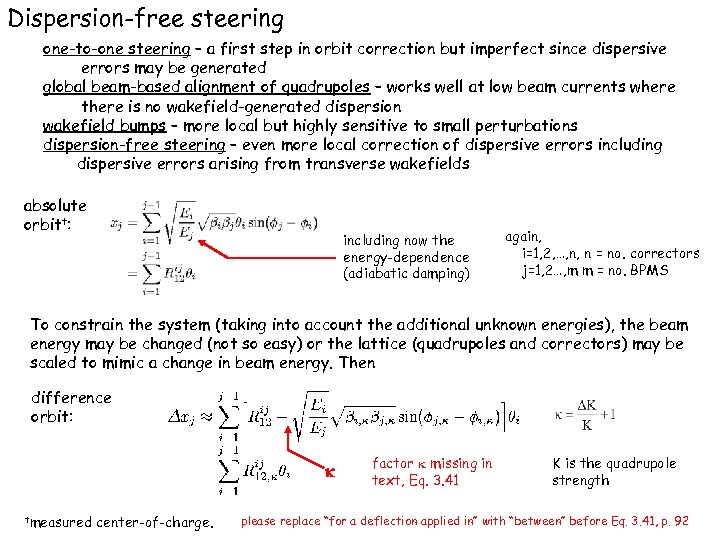
Dispersion-free steering one-to-one steering – a first step in orbit correction but imperfect since dispersive errors may be generated global beam-based alignment of quadrupoles – works well at low beam currents where there is no wakefield-generated dispersion wakefield bumps – more local but highly sensitive to small perturbations dispersion-free steering – even more local correction of dispersive errors including dispersive errors arising from transverse wakefields absolute orbitt: including now the energy-dependence (adiabatic damping) again, i=1, 2, …, n, n = no. correctors j=1, 2…, m m = no. BPMS To constrain the system (taking into account the additional unknown energies), the beam energy may be changed (not so easy) or the lattice (quadrupoles and correctors) may be scaled to mimic a change in beam energy. Then difference orbit: tmeasured center-of-charge. factor missing in text, Eq. 3. 41 K is the quadrupole strength please replace “for a deflection applied in” with “between” before Eq. 3. 41, p. 92
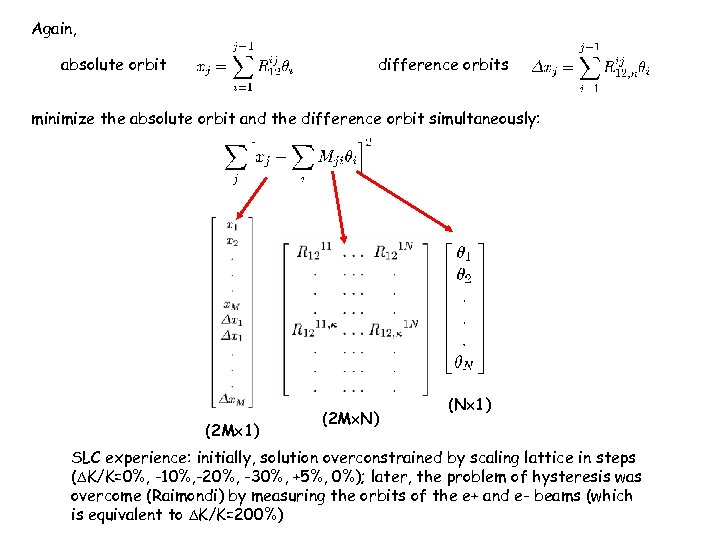
Again, absolute orbit difference orbits minimize the absolute orbit and the difference orbit simultaneously: (2 M 1) (2 M N) (N 1) SLC experience: initially, solution overconstrained by scaling lattice in steps ( K/K=0%, -10%, -20%, -30%, +5%, 0%); later, the problem of hysteresis was overcome (Raimondi) by measuring the orbits of the e+ and e- beams (which is equivalent to K/K=200%)
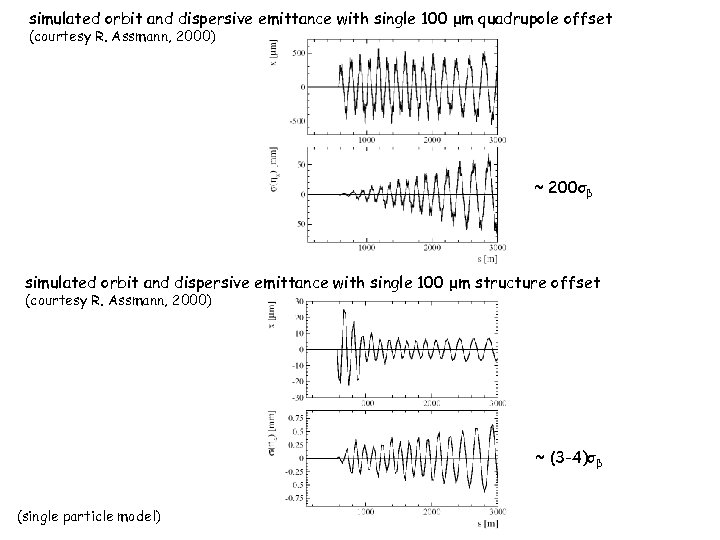
simulated orbit and dispersive emittance with single 100 μm quadrupole offset (courtesy R. Assmann, 2000) ~ 200σβ simulated orbit and dispersive emittance with single 100 μm structure offset (courtesy R. Assmann, 2000) ~ (3 -4)σβ (single particle model)
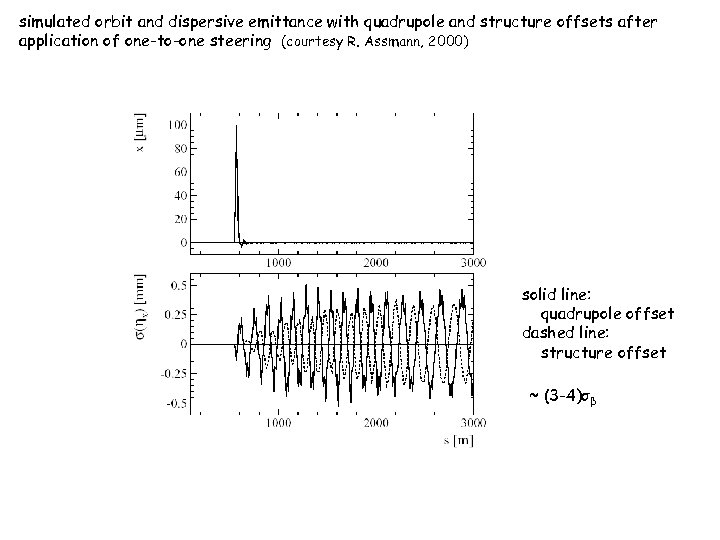
simulated orbit and dispersive emittance with quadrupole and structure offsets after application of one-to-one steering (courtesy R. Assmann, 2000) solid line: quadrupole offset dashed line: structure offset ~ (3 -4)σβ
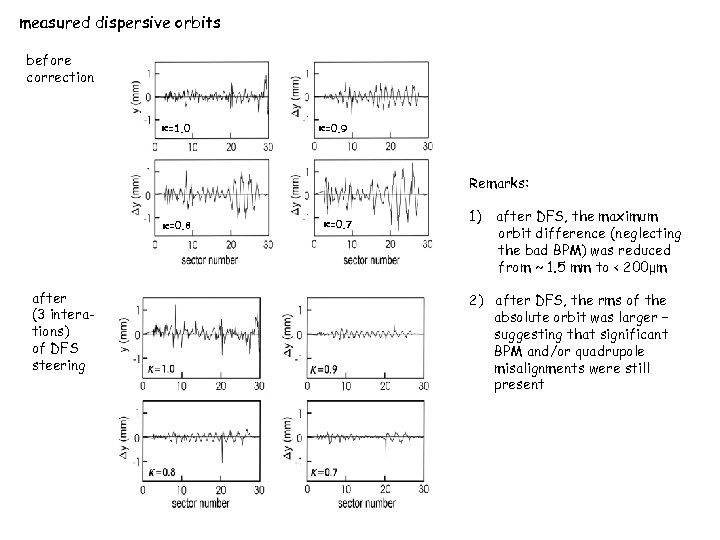
measured dispersive orbits before correction =1. 0 =0. 9 Remarks: =0. 8 after (3 interations) of DFS steering =0. 7 1) after DFS, the maximum orbit difference (neglecting the bad BPM) was reduced from ~ 1. 5 mm to < 200μm 2) after DFS, the rms of the absolute orbit was larger – suggesting that significant BPM and/or quadrupole misalignments were still present
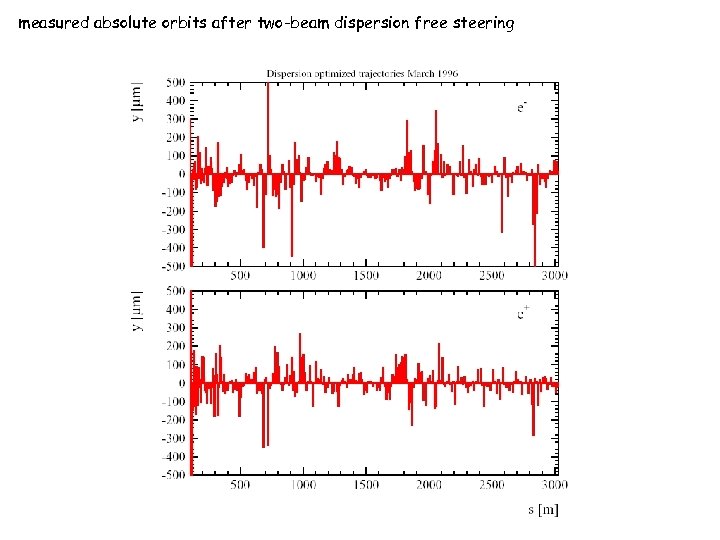
measured absolute orbits after two-beam dispersion free steering
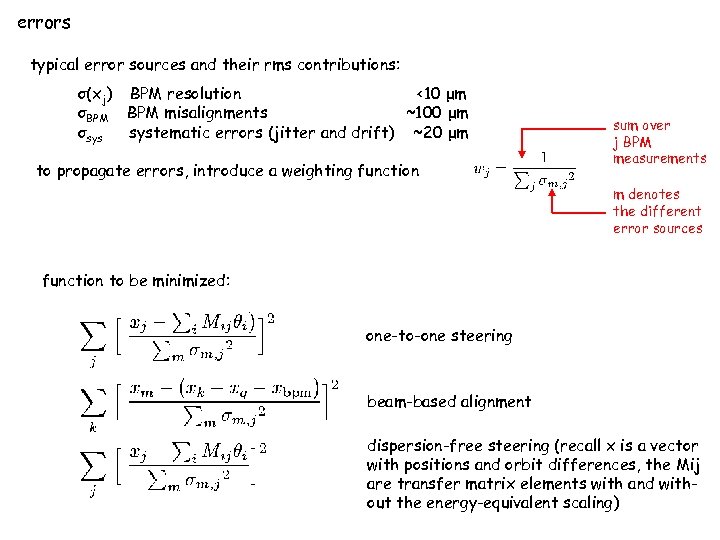
errors typical error sources and their rms contributions: σ(xj) BPM resolution <10 μm σBPM misalignments ~100 μm σsys systematic errors (jitter and drift) ~20 μm to propagate errors, introduce a weighting function sum over j BPM measurements m denotes the different error sources function to be minimized: one-to-one steering beam-based alignment dispersion-free steering (recall x is a vector with positions and orbit differences, the Mij are transfer matrix elements with and without the energy-equivalent scaling)
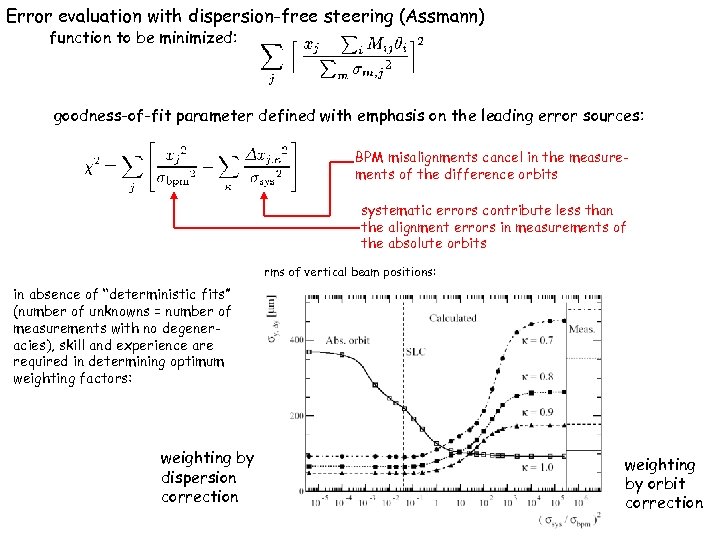
Error evaluation with dispersion-free steering (Assmann) function to be minimized: goodness-of-fit parameter defined with emphasis on the leading error sources: BPM misalignments cancel in the measurements of the difference orbits systematic errors contribute less than the alignment errors in measurements of the absolute orbits rms of vertical beam positions: in absence of “deterministic fits” (number of unknowns = number of measurements with no degeneracies), skill and experience are required in determining optimum weighting factors: weighting by dispersion correction weighting by orbit correction

Brief overview of some experiences with “higher-order” optics corrections at RHIC Dispersion due to skew quad errors, (kl) Coupling due to skew quad errors, (kl) Simultaneous minimization In practice, studies revealed that vertical dispersion was not dominated by skew quads but generated by the previously existing global coupling correction. The global coupling in turn was largely correcting for local coupling in the IRs due to rolls of the triplet quads (which was then corrected) “Simultaneous global coupling and vertical dispersion correction in RHIC”, C. Liu et al, NIM (2014)

Summary: Using the multipole field expansion, we discussed relative alignment errors and (some of) their effects on the beam (e. g. “feed-down effect”) Typical magnet-to-beam alignment tolerances, storage rings (i. e. synchrotron light sources): circular collider IPs (i. e. B-factories, HERA, LHC) linear collider IPs (i. e. NLC, TESLA) ~ 10 μm ~ 5 μm < 1 μm are considerably tighter than what can be achieved by precision alignment (surveying) which is on the order of (100 -200) m To overcome these difficulties, beam-based alignment and beam steering are used We reviewed various methods of beam-based alignment of single magnetic elements including various methods for aligning quadrupoles and sextupoles. As a precursor to beam steering methods, “lattice diagnostics” was presented, which is yet another method for localizing optics and BPM errors (the “bad BPMs” would then be excluded from steering algorithms) An example was presented, whereby an incomplete model with known shortcomings (as aften the case) could nonetheless provided information on optical and BPM errors

The steering method of choice (incidentally: unavoidable in large accelerators) depends on many factors including availability and reliability of BPMs relative importance of well-controlled orbits versus investment of effort relative importance versus investment of beam time prevailing conditions (i. e. presence of wakefields at high beam currents) Common methods of beam steering were described and algorithms were given for numerical analysis The methods presented included: one-to-one steering global beam-based alignment SVD steering (“wakefield bumps”) dispersion free steering Aspects of the mathematics were illustrated using simple examples 2 -corrector / 2 -BPM 2 minimization and SVD solution Completely overdetermined systems (as nowadays typical) require additional constraints (represented by the “weighting factors”), which implies non-deterministic solutions which require experience and skill to optimize Once optimal orbits have been determined, orbit feedback (not yet presented) may be used to maintain the orbits. The mechanics used by feedback are the same as used by the steering methods.

To Do All the above: assumes model is good Model versus reality (SWARM? ) Model with predictive power Tutorial on SVD and Least-Squares including “bad BPMs” and RHIC data available on request
9df5ab5f739a1c8763952c22f2ed0a2a.ppt