6-Lattice-spaceGroup.ppt
- Количество слайдов: 72

Translational symmetry Space Lattice or Bravais Lattice Symmetry. Screw axis Space group
Translational symmetry
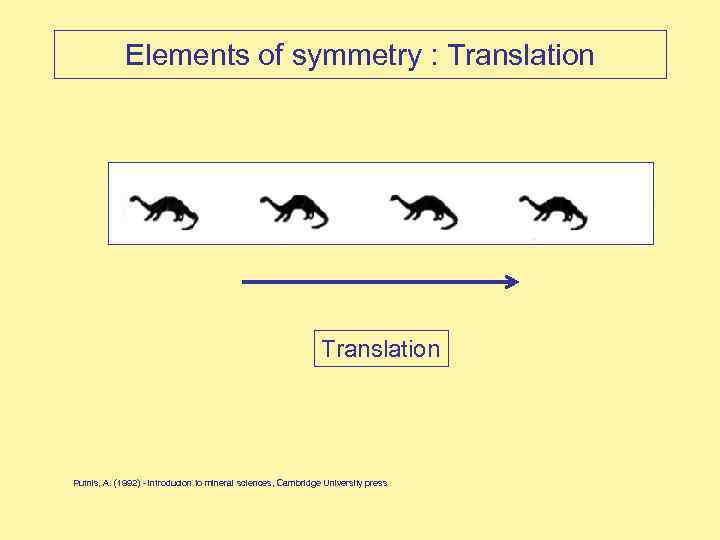
Elements of symmetry : Translation Putnis, A. (1992) - introducion to mineral sciences, Cambridge University press
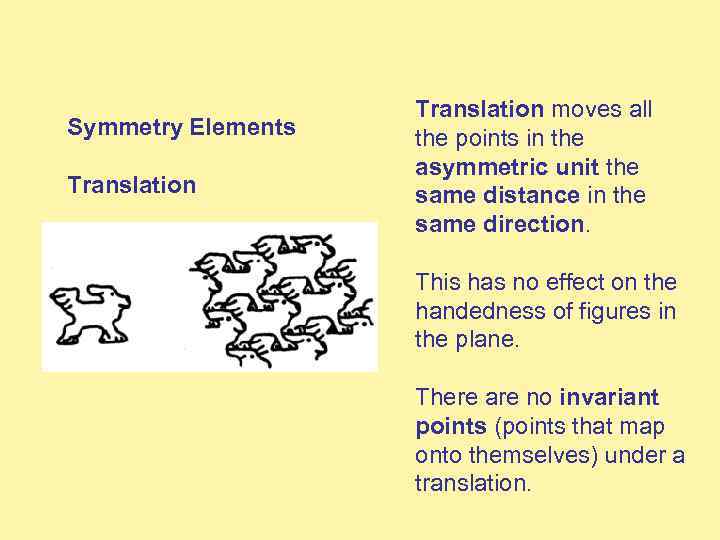
Symmetry Elements Translation moves all the points in the asymmetric unit the same distance in the same direction. This has no effect on the handedness of figures in the plane. There are no invariant points (points that map onto themselves) under a translation.
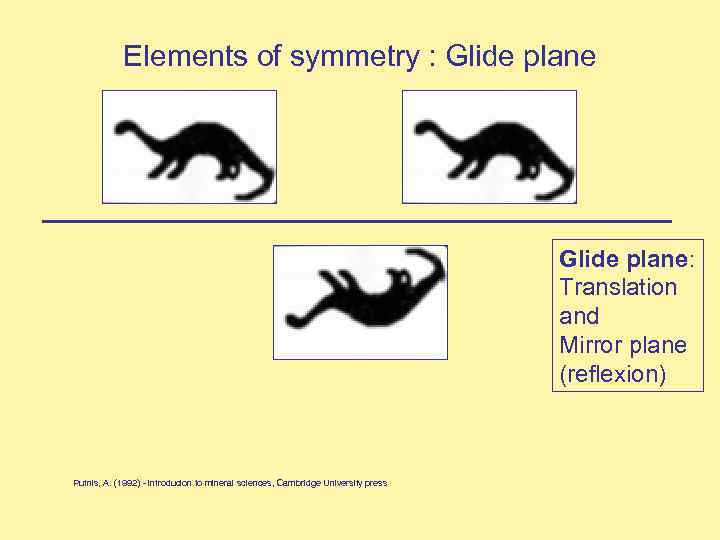
Elements of symmetry : Glide plane: Translation and Mirror plane (reflexion) Putnis, A. (1992) - introducion to mineral sciences, Cambridge University press
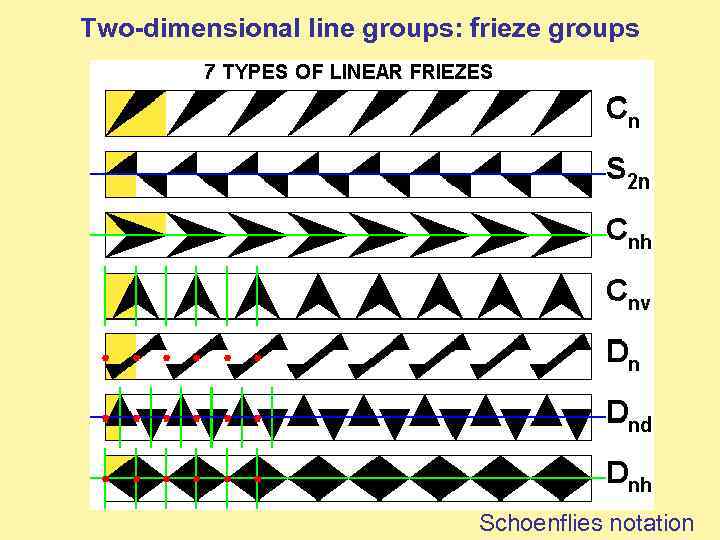
Two-dimensional line groups: frieze groups Schoenflies notation
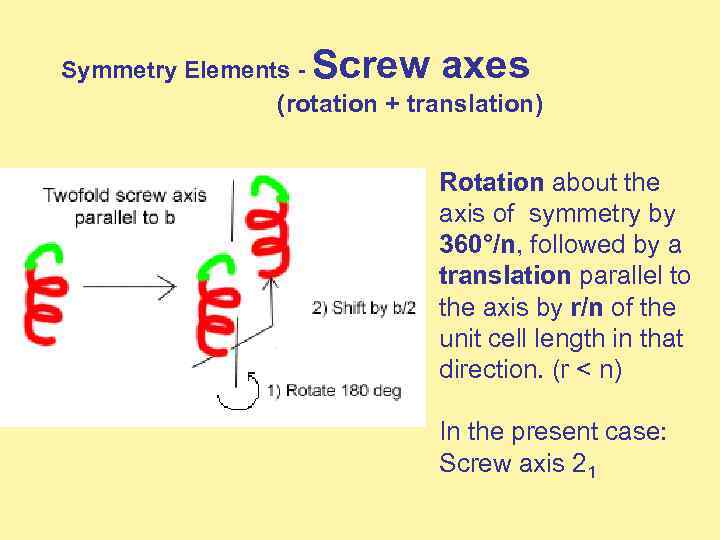
Screw axes Symmetry Elements (rotation + translation) Rotation about the axis of symmetry by 360°/n, followed by a translation parallel to the axis by r/n of the unit cell length in that direction. (r < n) In the present case: Screw axis 21
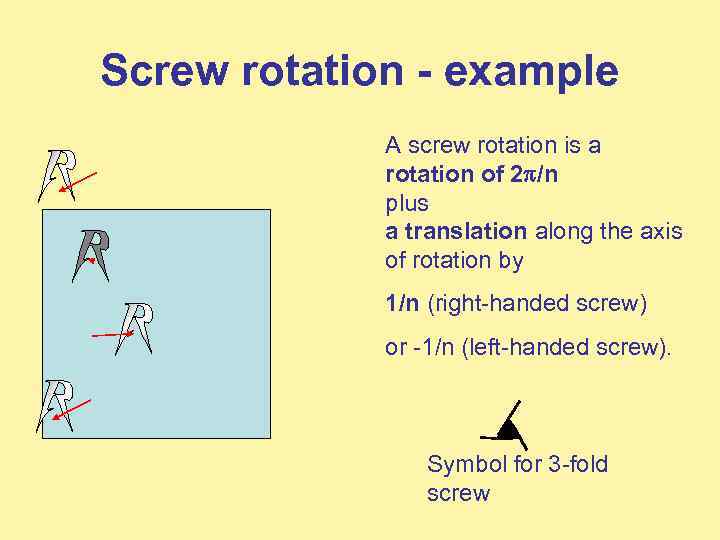
Screw rotation - example A screw rotation is a rotation of 2 /n plus a translation along the axis of rotation by 1/n (right-handed screw) or -1/n (left-handed screw). Symbol for 3 -fold screw
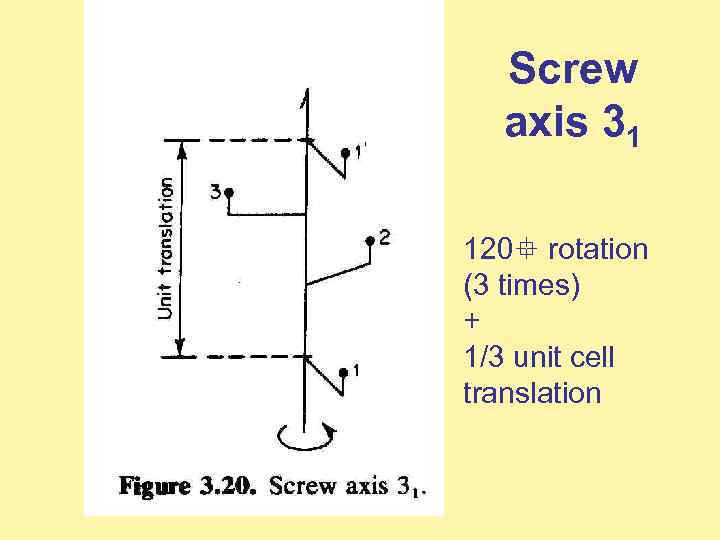
Screw axis 31 120 rotation (3 times) + 1/3 unit cell translation

Screw rotation 21 31 61 62 32 41 63 64 42 43 65 Example: 6 -4 fold in the projection. Screw moves up and to the right 4/6 units. Equivalent positions are related by rotation AND translation
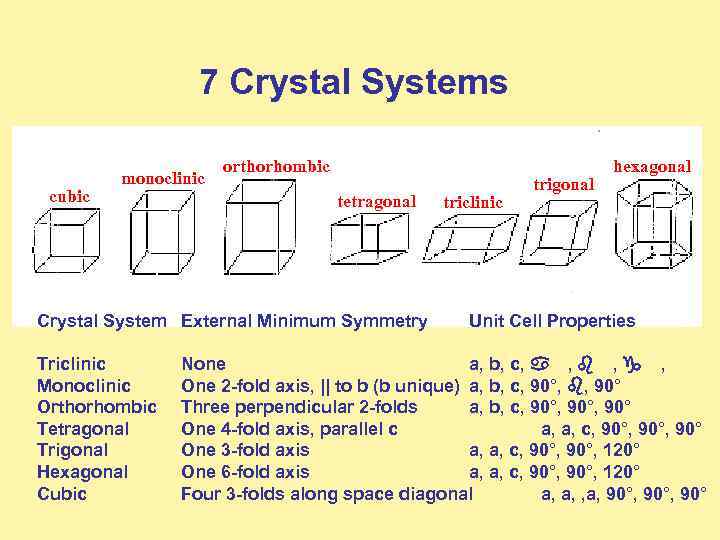
7 Crystal Systems cubic monoclinic orthorhombic tetragonal Crystal System External Minimum Symmetry Triclinic Monoclinic Orthorhombic Tetragonal Trigonal Hexagonal Cubic triclinic trigonal hexagonal Unit Cell Properties None a, b, c, , One 2 -fold axis, || to b (b unique) a, b, c, 90°, , 90° Three perpendicular 2 -folds a, b, c, 90°, 90° One 4 -fold axis, parallel c a, a, c, 90°, 90° One 3 -fold axis a, a, c, 90°, 120° One 6 -fold axis a, a, c, 90°, 120° Four 3 -folds along space diagonal a, a, 90°, 90°
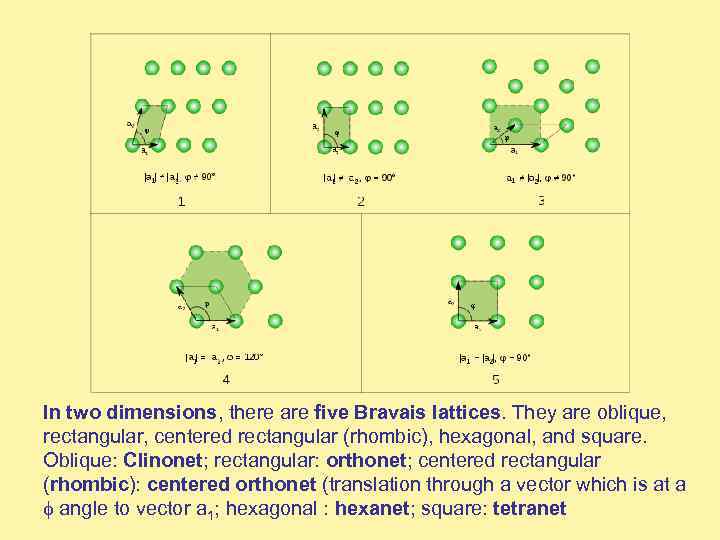
In two dimensions, there are five Bravais lattices. They are oblique, rectangular, centered rectangular (rhombic), hexagonal, and square. Oblique: Clinonet; rectangular: orthonet; centered rectangular (rhombic): centered orthonet (translation through a vector which is at a angle to vector a 1; hexagonal : hexanet; square: tetranet
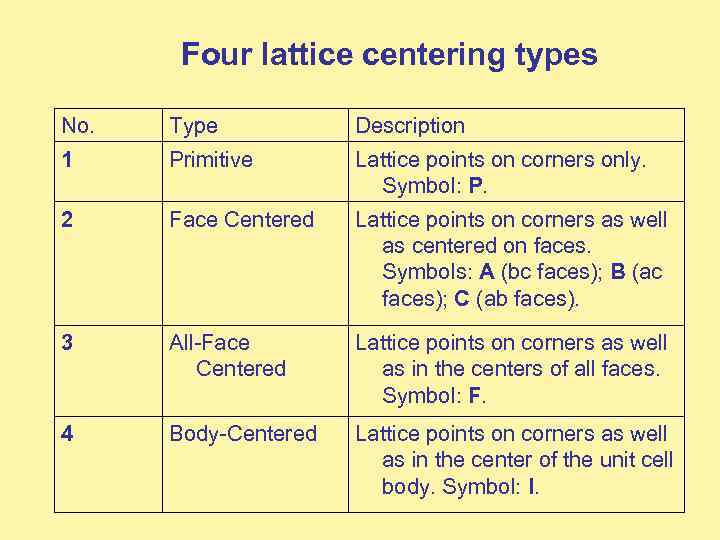
Four lattice centering types No. Type Description 1 Primitive Lattice points on corners only. Symbol: P. 2 Face Centered Lattice points on corners as well as centered on faces. Symbols: A (bc faces); B (ac faces); C (ab faces). 3 All-Face Centered Lattice points on corners as well as in the centers of all faces. Symbol: F. 4 Body-Centered Lattice points on corners as well as in the center of the unit cell body. Symbol: I.
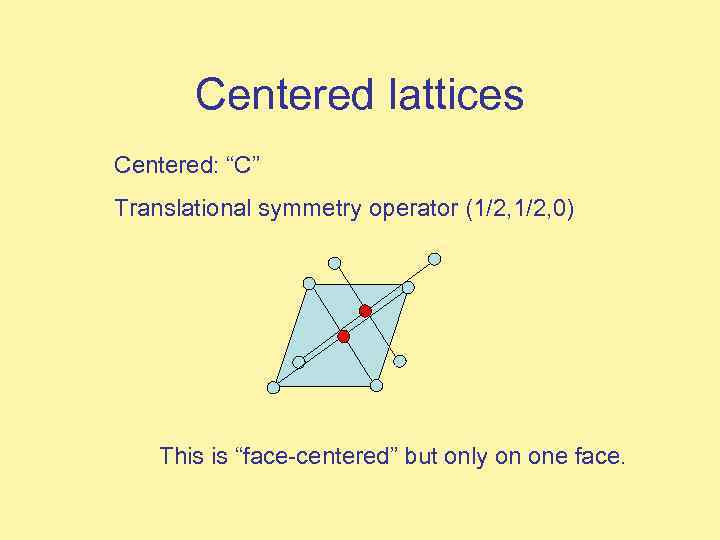
Centered lattices Centered: “C” Translational symmetry operator (1/2, 0) This is “face-centered” but only on one face.
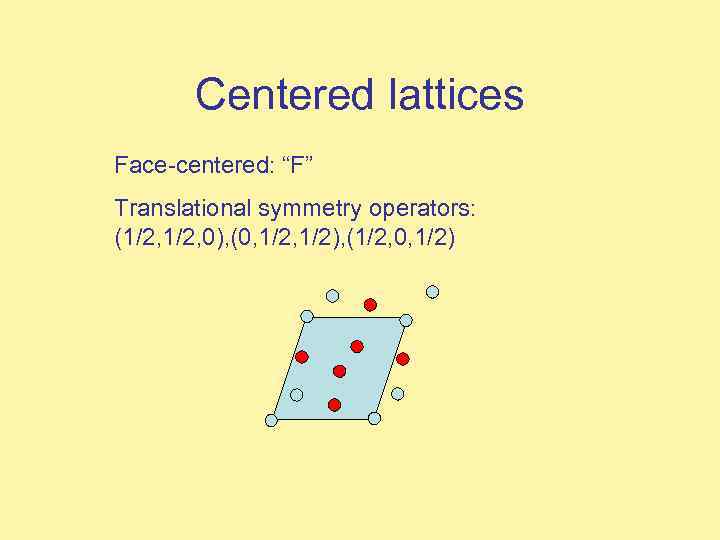
Centered lattices Face-centered: “F” Translational symmetry operators: (1/2, 0), (0, 1/2), (1/2, 0, 1/2)
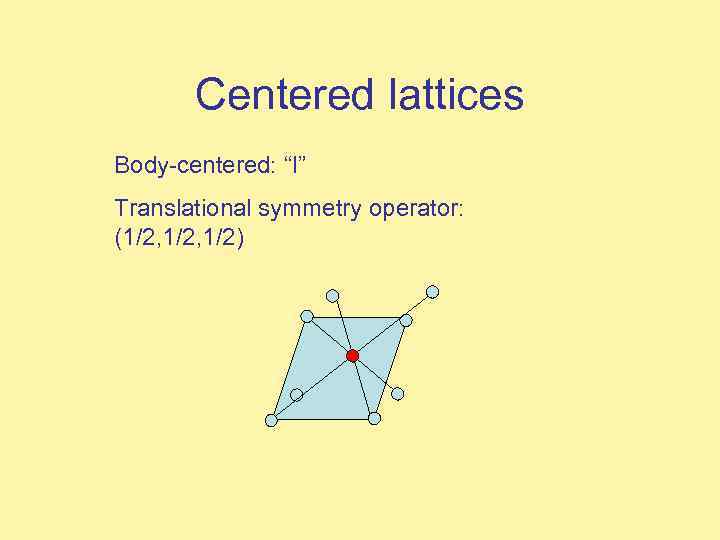
Centered lattices Body-centered: “I” Translational symmetry operator: (1/2, 1/2)
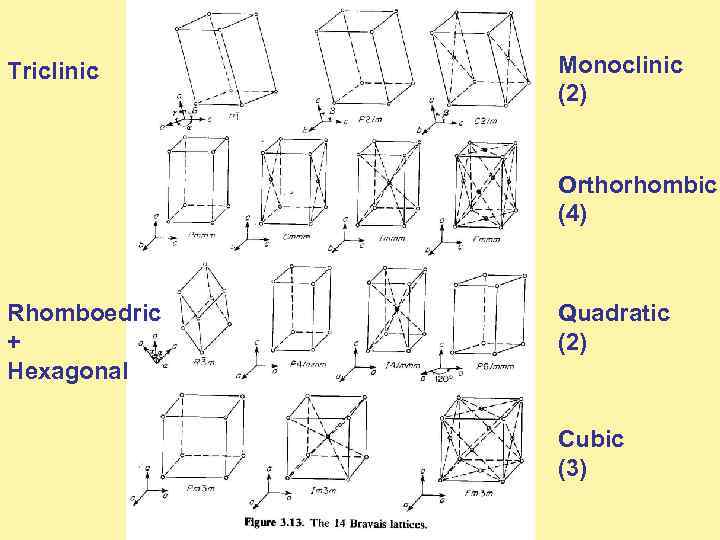
Triclinic Monoclinic (2) Orthorhombic (4) Rhomboedric + Hexagonal Quadratic (2) Cubic (3)

Auguste Bravais (1811 -1863) Lattices • In 1848, Auguste Bravais demonstrated that in a 3 -dimensional system there are fourteen possible lattices • A Bravais lattice is an infinite array of discrete points with identical environment • Seven crystal systems + four lattice centering types = 14 Bravais lattices • Lattices are characterized by translation symmetry

Tetragonal lattices are either primitive (P) or body-centered (I) C centered lattice = Primitive lattice
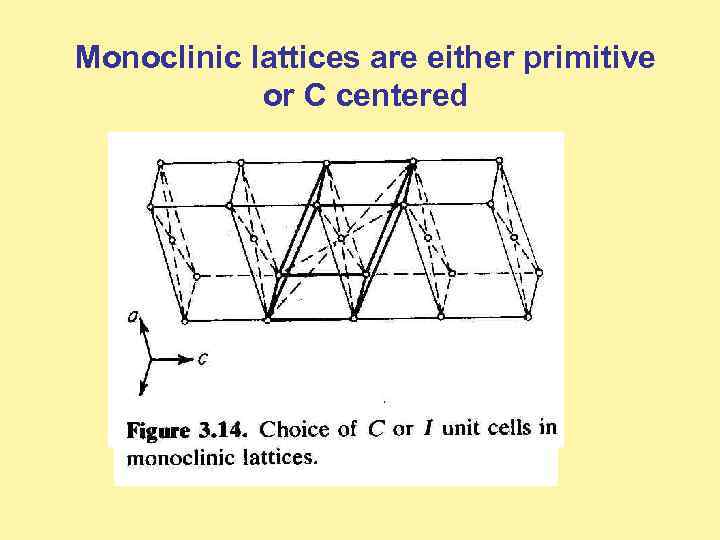
Monoclinic lattices are either primitive or C centered

Definition Lattice - The concept of a lattice is directly related to the idea of translational symmetry. A lattice is a network or array composed of a single motif which has been translated and repeated at fixed intervals throughout space. In a crystal, the atoms show an internal ordered arrangement in three dimensions. The three dimensional network is referred as a lattice.
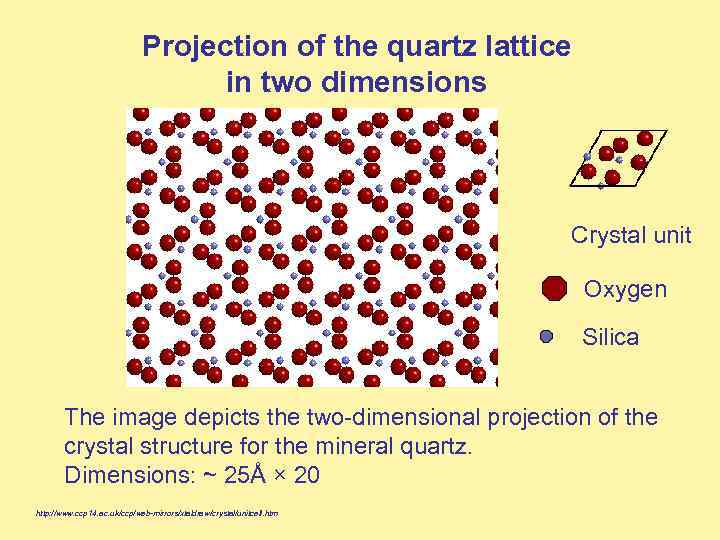
Projection of the quartz lattice in two dimensions Crystal unit Oxygen Silica The image depicts the two-dimensional projection of the crystal structure for the mineral quartz. Dimensions: ~ 25Å × 20 http: //www. ccp 14. ac. uk/ccp/web-mirrors/xtaldraw/crystal/unitcell. htm
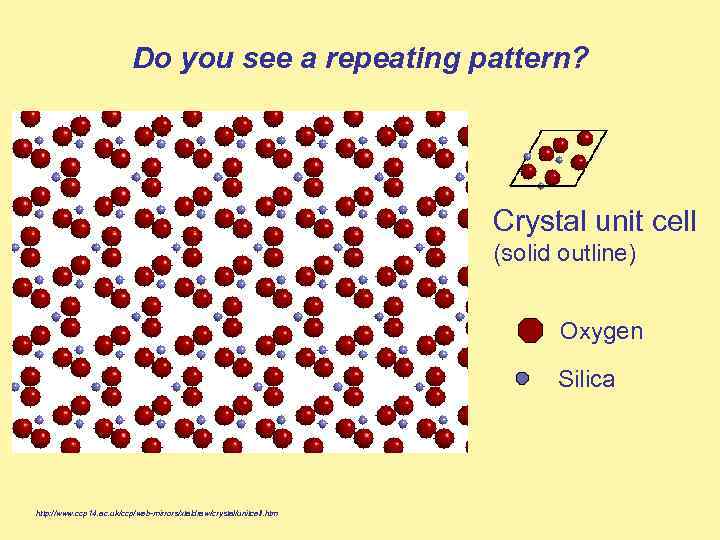
Do you see a repeating pattern? Crystal unit cell (solid outline) Oxygen Silica http: //www. ccp 14. ac. uk/ccp/web-mirrors/xtaldraw/crystal/unitcell. htm
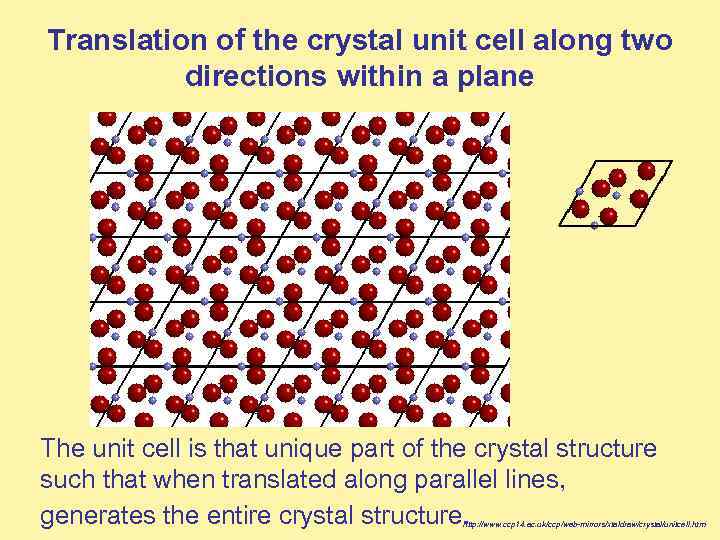
Translation of the crystal unit cell along two directions within a plane The unit cell is that unique part of the crystal structure such that when translated along parallel lines, generates the entire crystal structure. http: //www. ccp 14. ac. uk/ccp/web-mirrors/xtaldraw/crystal/unitcell. htm
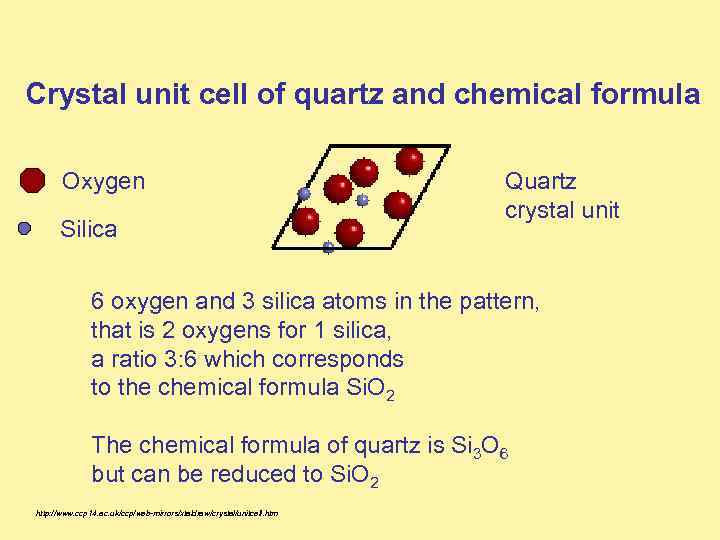
Crystal unit cell of quartz and chemical formula Oxygen Silica Quartz crystal unit 6 oxygen and 3 silica atoms in the pattern, that is 2 oxygens for 1 silica, a ratio 3: 6 which corresponds to the chemical formula Si. O 2 The chemical formula of quartz is Si 3 O 6 but can be reduced to Si. O 2 http: //www. ccp 14. ac. uk/ccp/web-mirrors/xtaldraw/crystal/unitcell. htm
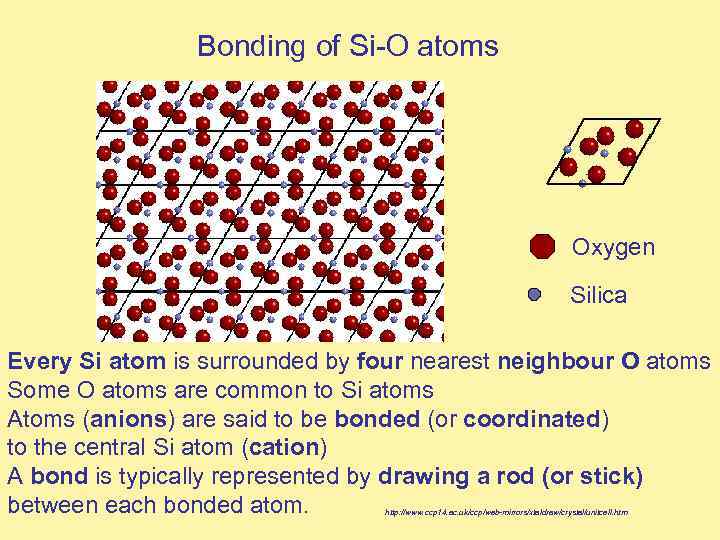
Bonding of Si-O atoms Oxygen Silica Every Si atom is surrounded by four nearest neighbour O atoms Some O atoms are common to Si atoms Atoms (anions) are said to be bonded (or coordinated) to the central Si atom (cation) A bond is typically represented by drawing a rod (or stick) between each bonded atom. http: //www. ccp 14. ac. uk/ccp/web-mirrors/xtaldraw/crystal/unitcell. htm

Projection of the quartz lattice in 3 dimensions Oxygen Silica To complete the coordination sphere of each Si, additional Si and O must be drawn outside of the initial pattern, giving a view of the three-dimensional crystal structure of the mineral quartz http: //www. ccp 14. ac. uk/ccp/web-mirrors/xtaldraw/crystal/unitcell. htm
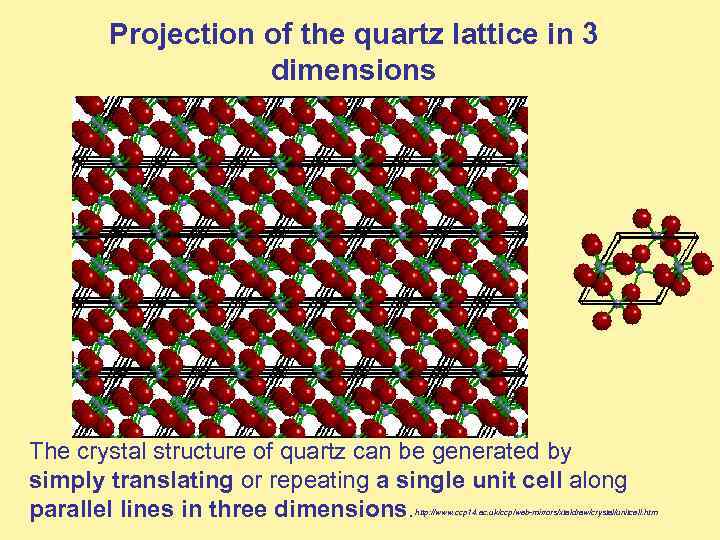
Projection of the quartz lattice in 3 dimensions The crystal structure of quartz can be generated by simply translating or repeating a single unit cell along parallel lines in three dimensions. http: //www. ccp 14. ac. uk/ccp/web-mirrors/xtaldraw/crystal/unitcell. htm

Definition Lattice - The concept of a lattice is directly related to the idea of translational symmetry. A lattice is a network or array composed of a single motif which has been translated and repeated at fixed intervals throughout space. In a crystal, the atoms show an internal ordered arrangement in three dimensions. The three dimensional network is referred as a lattice.

Definition The unit cell of a lattice is the smallest unit which can be repeated in three dimensions in order to construct the lattice. In a crystal, the unit cell consists of a specific group of atoms which are bonded to one another in a set geometrical arrangement. The corners of the unit cell therefore serve as points which are repeated to form a lattice array; these points are termed lattice points. The vectors which connect a straight line of equivalent lattice points and delineate the edges of the unit cell are known as the crystallographic axes. (http: //dave. ucsc. edu/myrtreia/crystal. html#SYMMETRY).

Height: 5. 5 cm Hauy’s wood models The wood model represents a dodecahedron with pentagonal faces (pyritohedron) constructed from a cubic nucleus by decrement of two rows of "integrant cubic molecules » . The model edges show 17 cubic "molecules » . http: //www. mineralogy. eu/models/pyritohedron 01. html

Height: 7 cm Hauy’s wood models The model illustrates a complex differential decrement of cubic "molecules" on the edges and on the vertices. http: //www. mineralogy. eu/models/pyritohedron 01. html Haüy - R. J. Annales de Chimie, 17, 225 -319 (1793)

Space group - In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains. In crystallography, they are also called the crystallographic or Fedorov groups, and represent a description of the symmetry of the crystal. A definitive source regarding 3 -dimensional space groups is the International Tables for Crystallography (Hahn 2002).

Space group The space groups in three dimensions are made from combinations of the 32 crystallographic point groups with the 14 Bravais lattices, each of the latter belonging to one of 7 crystal systems.

Space group This results in a space group being some combination of the translational symmetry of a unit cell including lattice centering, the point group symmetry operations of reflection, rotation and improper rotation (also called rotoinversion), and the screw axis and glide plane symmetry operations. The combination of all these symmetry operations results in a total of 230 different space groups describing all possible crystal symmetries.
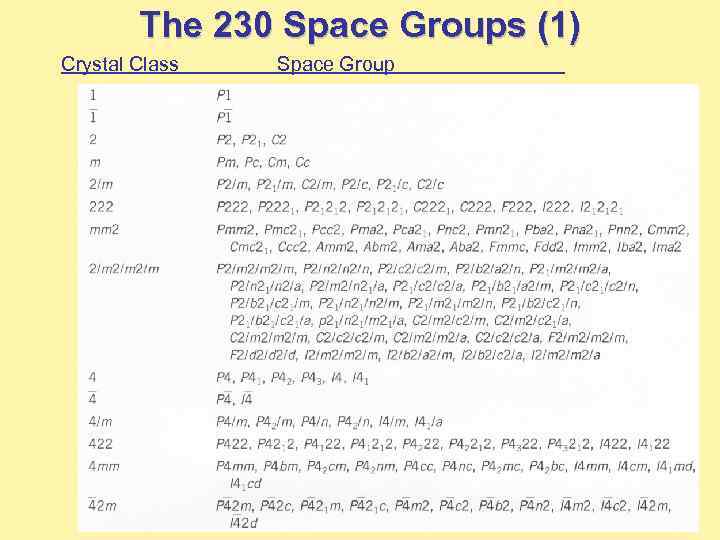
The 230 Space Groups (1) Crystal Class Space Group
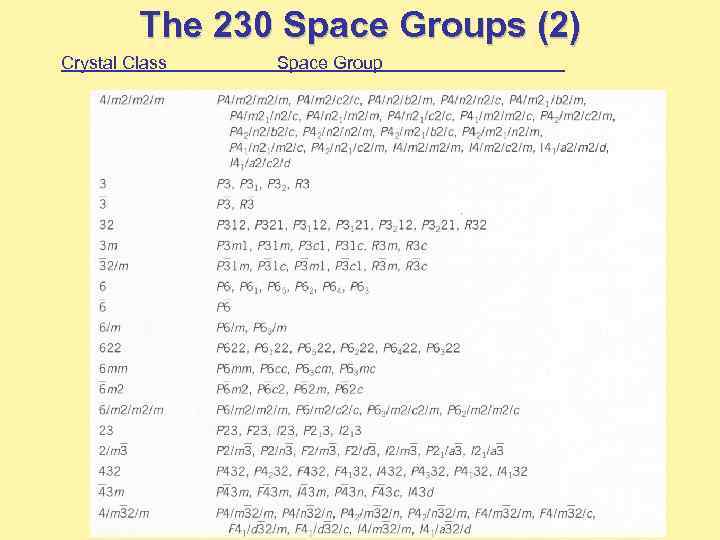
The 230 Space Groups (2) Crystal Class Space Group

Symmetry and matrice notation

Symmetry An object or function is symmetrical if a spatial transformation of it looks identical to the original. X This is rotated by 180° X This is the original

Types of symmetry operations • Point of inversion • mirror plane • rotation (2, 3, 4 or 6 -fold) • translation • glide plane • screw axis • lattice symmetry

Mathematical Definition • Define geometric transformations: – reflection, rotation, translation (“slide”), – glide reflection (“slide and reflect”), identity, … • A symmetry is a transformation • The symmetries of an object are the set of transformations which leave object looking unchanged • Think of symmetries as axes, mirror lines, …

Symmetry operators A spatial transformation can be expressed as an operator that changes the coordinates of every point in the object the same way. Symmetry operators do not distort the object. In other words, the distance between any two points is the same before and after being moved by the symmetry operation. Here is the operator for a 180° rotation around Z. equivalent positions

REMINDER 3 x 3 Matrix multiplication http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

Fractional coordinates The crystallographic coordinate system is defined by the unit cell. The location of a point is defined by fraction of traveled (from 0 to 1) along each unit cell axis. c (0. 33, 0. 25, 0. 55) b a Fractional coordinates are always measured parallel to each axis. The axes are not necessarily 90° apart! http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

Centre of symmetry - point of inversion http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

Mirror plane http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

Glide plane x http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

Rotation http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

screwrotation 120° 1/3 of a unit cell http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

Rotational symmetry A 2 -fold (180°) rotation around the Z-axis http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

Rotation matrices. . . the mathematical description of a rotation. y axis of rotation (x’, y’) r atom starts here. . . rotates by b. . . goes here (x, y) x In polar coordinates, a rotation is the addition of angles. http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

REMINDER: sum of angles rules cos ( = cos sin ( = sin cos http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

Adding angles in Cartesian space converting internal motion to Cartesian motion y x = |r|cos (x’, y’) y = |r|sin r (x, y) x x' = |r| cos ( y' = |r| sin ( = |r|(cos sin = |r|(sin cos = (|r| cos |r| sin = (|r| sin cos |r| cos sin = x cos y sin = y cos x sin in matrix notation. . . rotation matrix http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

2 D rotation using matrix notation “row times column” x' = x cos y sin = = (|r| cos |r| sin = |r| cos ( y' = y cos x sin = (|r| sin cos |r| cos sin = |r| sin ( http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

Transposing the matrix reverses the rotation To rotate the opposite direction, flip the matrix about the diagonal. the “transpose” inverse rotation matrix = transposed rotation matrix. . because cos + sin = 1 http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

A 3 D rotation matrix Is the product of 2 D rotation matrices. Ro tat ion Ro tat aro un ion 3 D aro tat un dz -ax is http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf ro dy -ax is ion

Example: Rotate v=(1. , 2. , 3. ) around Z by 60°, then rotate around Y by -60° http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf
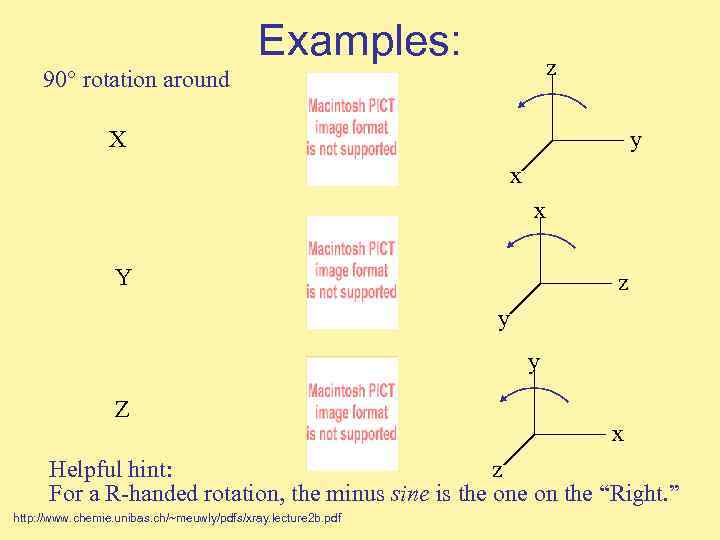
Examples: z 90° rotation around X y x x Y z y y Z x Helpful hint: z For a R-handed rotation, the minus sine is the on the “Right. ” http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

Properties of rotation matrices • Square, 2 x 2 or 3 x 3 • The product of any two rotation matrices is a rotation matrix • The inverse equals the transpose, R-1 = RT • orthogonality • The dot-product of any row or column with itself is one. • The dot-product of any row or column with a different row or column is zero. • |x| equals |Rx|, for any rotation R. More at http: //mathworld. wolfram. com/Rotation. Matrix. html

2 -fold rotation R 2 -fold symbol P 2 R 180° rotation. Called a 2 -fold because doing it twice brings you back to where you started. http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf Equivalent positions in fractional coordinates: x, y, z -x, -y, z

3 -fold symbol R P 3 R R 3 -fold rotation In fractional coordinates: Equivalent positions : x, y, z http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf -y, x-y, z -x+y, -x, z

4 -fold rotation R R P 4 R R 4 -fold symbol In fractional coordinates (same as orthogonal coords): Equivalent positions: http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf x, y, z -y, x, z -x, -y, z y, -x, z

6 -fold rotation R R R P 6 RR R In fractional coordinates: 6 -fold symbol Equivalent positions: x, y, z -x, -y, z http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf -y, x-y, z y, -x+y, z -x+y, -x, z x-y, x, z

Space groups A symmetry “group” is a set of symmetry operators that is closed, meaning any two operations, applied in succession, create a third operation that is part of the group. A “space group” is a symmetry group that includes lattice symmetry operators. All space groups implicitly include lattice operators: (± 1 , ± 1)

Group theory A space group is a closed set of operators. If you apply any two operators in succession. the result is another one of the operators in the group. Equivs for P 21: (x, y, z), (-x, -y, z+1/2) http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

Space groups The combination of all available symmetry operations (32 point groups), together with translation symmetry, within the all available lattices (14 Bravais lattices) lead to 230 Space Groups that describe the only ways in which identical objects can be arranged in an infinite lattice. The International Tables list those by symbol and number, together with symmetry operators, origins, reflection conditions, and space group projection diagrams. http: //www. chemie. unibas. ch/~meuwly/pdfs/xray. lecture 2 b. pdf

Space groups Cell type P, C, I or F I=body centered I 4122 Principle axis of symmetry is 4 -fold screw Secondary axes of symmetry are proper 2 -folds

The International Tables for Crystallography Equivalent positions: (x, y, z), (-x, -y, z+1/2)
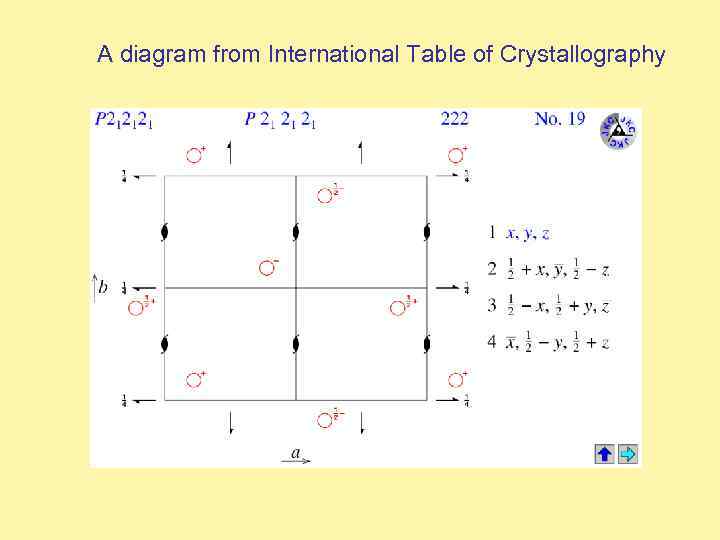
A diagram from International Table of Crystallography

Identification of the Space Group is called indexing the crystal. The International Tables for X-ray Crystallography tell us a huge amount of information about any given space group. For instance, if we look up space group P 2, we find it has a 2 -fold rotation axis and the following symmetry equivalent positions: X , Y , Z -X , Y , -Z and an asymmetric unit defined by: 0 ≤ x ≤ 1 0 ≤ y ≤ 1 0 ≤ z ≤ 1/2 An interactive tutorial on Space Groups can be found on-line in Bernhard Rupp’s Crystallography 101 Course: http: //wwwstructure. llnl. gov/Xray/tutorial/spcgrps. htm

Cubic space group P 213 x, y, z -x+1/2, -y, z+1/2 -x, y+1/2, z+1/2 x+1/2, -y+1/2, -z z, x, y z+1/2, -x+1/2, -y -z+1/2, -x, y+1/2 -z, x+1/2, -y+1/2 y, z, x -y, z+1/2, -x+1/2 y+1/2, -z+1/2, -x -y+1/2, -z, x+1/2

6-Lattice-spaceGroup.ppt