Transforming DEVS to Non-Modular Form For Faster Cellular

Transforming DEVS to Non-Modular Form For Faster Cellular Space Simulation Fahad A. Shiginah, Bernard P. Zeigler {shiginah, zeigler}@ece. arizona. edu Arizona Center for Integrative Modeling and Simulation Electrical and Computer Engineering Department University of Arizona

Content n n n n Introduction Cellular Space Modeling Cellular Models in DEVS The New Approach for Message Reduction Transforming to Non-Modular DEVS Experimental Results Conclusions

Introduction n n n DEVS has been attracting researchers as a basis of Cellular modeling in complex physical systems. Parallel DEVS made it possible to implement cellular models in DEVS models are modular units that can access the states of other models through message passing. Representing cellular spaces in modular DEVS resulted in having cells communicating with each other to know neighboring states. In large scale cellular space, huge number of inter-cell messages will be employed which result in performance reduction. To overcome this problem, the non-modular form of DEVS should be consider as an alternative for faster large cellular space simulations.

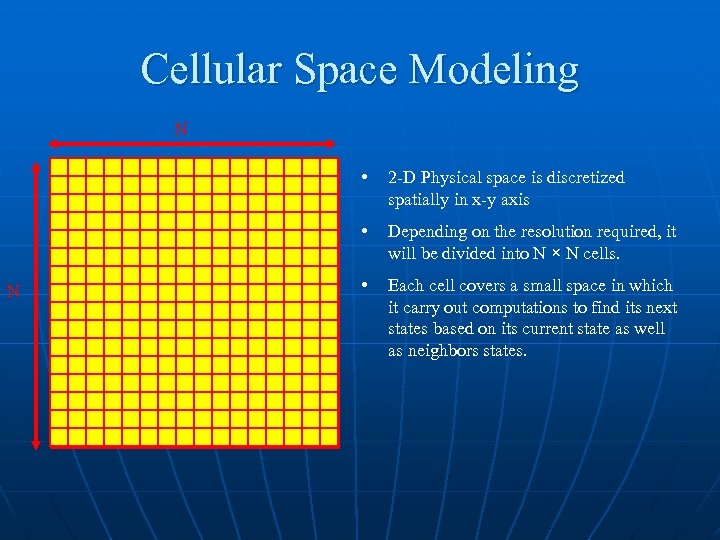Cellular Space Modeling N • • N 2 -D Physical space is discretized spatially in x-y axis Depending on the resolution required, it will be divided into N × N cells. • Each cell covers a small space in which it carry out computations to find its next states based on its current state as well as neighbors states.

Cellular Models in DEVS N • A cell is implemented as DEVS atomic model. • The whole cellular space will be a coupled/hierarchical model containing all cells (atomic models). • Modularity in DEVS allow cell to communicate through ports only. • Each cell calculates its next state based on its current state and external inputs from neighbors (if exists at ports). • All cells run in parallel (Parallel DEVS) • Simulation continues until all cells are in passive mode or reaches a predefined stopping point. N

Encapsulation Scheme • Our goal is to reduce number of intercell communication. • The new encapsulation will divide the cellular space into smaller subspace. • Each subspace will encapsulate a group of cells. • In each subspace, cells will be arranged in arrays to preserve their states and variables where they can access their neighbors states directly. • This eliminates the ports and messages between all cells in one subspace where ports will be needed at the boundaries of the subspace only. • Now, subspace is implemented as DEVS atomic model having ports to carry out the communication between cells at the boundaries. N N

Messages in conventional Approach In a cellular space of N × N dimension, each cell can send messages to its 4 neighboring cells (Neumann neighbors). Assuming that in a single iteration a cell will send V messages in each of the 4 directions as the worst case scenario. The conventional approach will result in 4 VN 24 VN messages per iteration given that the cells at the boundaries will not send to at least one of its neighbors.

Message Reduction in Our Approach That cellular space of N × N dimension can be divided into S × S subspaces (Atomic DEVS) with N 2/S 2 internal cells each. A subspace will just send VN/S in each direction and the total number of messages per iteration will be 4 VNS-4 VN given that the subspaces at the boundaries will not send to at least one of its neighbors. The percentage reduction of messages will be (N-S)/(N-1)% which will result in 100% reduction if S=1 or 0% if S=N.

Review: Parallel DEVS [1] Atomic DEVS Model (M) M = < X, Y, S, δint, δext, δcon, λ, ta> X is a set of input values. S is a set of states. Y is a set of output values. δint : S S is the internal transition function. δext : Q × Xb S is the external transition function, where Q = {(s, e) | s S, 0 ≤ e ≤ ta(s)} is the total state set e is the time elapsed since last transition Xb denotes the collection of bags over X δcon : Q × Xb S is the confluent transition function, λ: S Yb is the output function CM= X is the set of input values. Y is the set of output values. D is the set of components. for each i in D: Mi is a component which is an atomic model Mi = < Xi, Yi , Si , δint i , δext i , δcon i , λi, tai> for each i in D {self}: Ii is the influencees of i, i is not in Ii. self is the coupled model itself CM which allow external inputs and outputs. for each j in Ii : Zi, j is the i to j output translation function (coupling). Zself, j : Xself Xj Zi, self : Yi Yself Zi, j : Xi Yj ta: S R 0 ∞ is the time advance function. Coupled DEVS Model (CM)

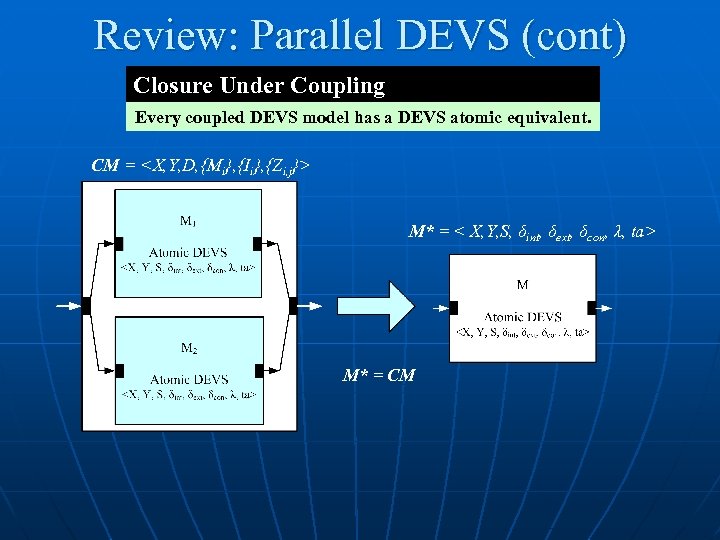Review: Parallel DEVS (cont) Closure Under Coupling Every coupled DEVS model has a DEVS atomic equivalent. CM = M* = < X, Y, S, δint, δext, δcon, λ, ta> M* = CM

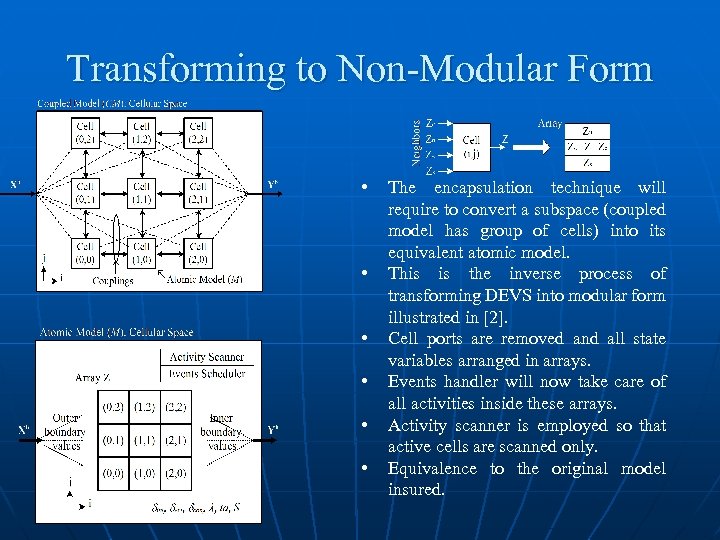Transforming to Non-Modular Form • • • The encapsulation technique will require to convert a subspace (coupled model has group of cells) into its equivalent atomic model. This is the inverse process of transforming DEVS into modular form illustrated in [2]. Cell ports are removed and all state variables arranged in arrays. Events handler will now take care of all activities inside these arrays. Activity scanner is employed so that active cells are scanned only. Equivalence to the original model insured.

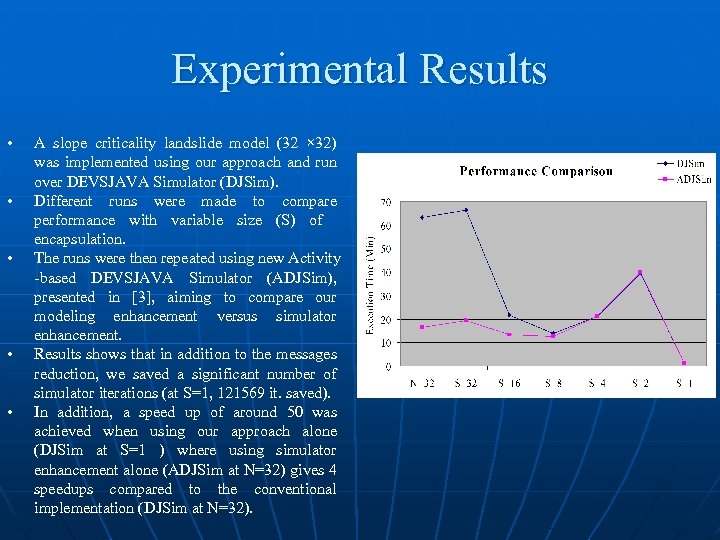Experimental Results • • • A slope criticality landslide model (32 × 32) was implemented using our approach and run over DEVSJAVA Simulator (DJSim). Different runs were made to compare performance with variable size (S) of encapsulation. The runs were then repeated using new Activity -based DEVSJAVA Simulator (ADJSim), presented in [3], aiming to compare our modeling enhancement versus simulator enhancement. Results shows that in addition to the messages reduction, we saved a significant number of simulator iterations (at S=1, 121569 it. saved). In addition, a speed up of around 50 was achieved when using our approach alone (DJSim at S=1 ) where using simulator enhancement alone (ADJSim at N=32) gives 4 speedups compared to the conventional implementation (DJSim at N=32). Message Reduction (%) Iterations N=32 0 S=32 Execution Time (Min) DJSim ADJSim 171478 63. 17 16. 56 0 171478 66. 35 19. 29 S=16 51. 60 150149 21. 73 13. 43 S=8 77. 40 126171 13. 89 12. 61 S=4 90. 30 124755 21. 22 21. 06 S=2 96. 70 124755 39. 53 40. 04 S=1 100 49909 1. 36

CONCLUSION n The new approach significantly enhances the performance of cellular space simulation in DEVS because of the following: • Reducing inter-cell communications • Reducing number of simulator iterations that deals with messages only. • Efficiently scan active cells in the system only. n n n Simulation restructuring does not deal with inter-cell messaging overhead. Therefore, both model and simulator enhancements must by employed together to simulate large scale cellular modeling environments. Best performance was achieved when all cells are in one atomic model. This may give a great enhancement in distributed cellular simulation by transforming the subcellular space in a single machine entirely into non-modular form. Further investigation is required to test our approach on large distributed cellular space simulation to justify this claim. The new approach can be applied to any other non-hierarchal cellular model. However, applying it manually is complex and error prone. An automated way of conversion needs to be implemented for fast, accurate conversion process.

REFERENCES 1. 2. 3. Chow, A. C. , and Zeigler, B. P. 1994. “Parallel DEVS: a parallel, hierarchical, modular modeling formalism and its distributed simulator”. In Winter Simulation Conference Proceedings, Orlando, FL. Zeigler, B. P. , Kim T. , and Praehofer, H. 2000. Theory of Modeling and Simulation: Integrating Discrete Event and Continuous Complex Dynamic Systems. Academic Press. Hu, X. , and Zeigler, B. P. 2004. “A High Performance Simulation Engine for Large-Scale Cellular DEVS Models”. High Performance Computing Symposium (HPC'04), Advanced Simulation Technologies Conference.