234915a9d7b1d6513af36119f1da7712.ppt
- Количество слайдов: 45

Transactions Controlling Concurrent Behavior

Busy, busy. . . • In production environments, it is unlikely that we can limit our system to just one user at a time. – Consequently, it is possible for multiple queries or transactions to be submitted at approximately the same time. • If all of the queries were very small (i. e. , in terms of time), we could probably just execute them on a first come first served basis. • However, many queries are both complex and time consuming. – Executing these queries would make other queries wait a long time for a chance to execute. • So, in practice, the DBMS may be running many different transactions at about the same time.

Concurrent Transactions • Unlike operating systems, which support interaction of processes, a DMBS needs to keep processes from troublesome interactions. • Even when there is no “failure, ” several transactions can interact to turn a consistent state into an inconsistent state.

Transactions • A process that reads or modifies the DB is called a transaction. • It’s a unit of execution of database operations. Basic JDBC transaction pattern Connection conn =. . . ; conn. set. Auto. Commit(false); try {. . . //JDBC statements } finally { conn. commit(); }

COMMIT and ROLLBACK • The SQL statement COMMIT causes a transaction to complete. – It’s database modifications are now permanent in the database. • The SQL statement ROLLBACK also causes the transaction to end, but by aborting. – No effects on the database. • Failures like division by 0 or a constraint violation can also cause rollback, even if the programmer does not request it.

ACID Transactions • ACID transactions are: – Atomic : Whole transaction or none is done. – Consistent : Database constraints preserved. – Isolated : It appears to the user as if only one process executes at a time. • That is, even though actions of several transactions might be interleaved, the net effect is identical to executing all transactions one after another in some serial order. – Durable : Effects of a process survive a crash. • Optional: weaker forms of transactions are often supported as well.

Interleaving • For performance reasons, a DBMS has to interleave the actions of several transactions. However, the interleaving must be done carefully… • Consider two transactions T 1 and T 2, each of which, when running alone preserves database consistency: – T 1 transfers $100 from A to B, and – T 2 increments both A and B by 1% (e. g. daily interest) – Consider the following interleaving. (1) T 1 deducts $100 from A, (2) T 2 increments both A and B by 1%, (3) T 2 adds $100 to B. – What’s the problem? – B just lost $1.

Transactions and Schedules • A transaction is a list of actions. The actions could be: – read, write, commit, abort • A schedule is a list of actions from a set of transactions. E. g. T 1 r(A) w(A) T 2 r(B) w(B) commit r(C) w(C) commit

Anomalies: Reading Uncommitted Data T 1 r(A) w(A) T 2 r(A) w(A) r(B) w(B) commit • T 1 transfers $100 from A to B, and • T 2 increments both A and B by 1% (e. g. daily interest) • The problem is that the bank didn’t pay interest on the $100 that was being transferred. • Of course there would be no problem if we executed T 1 and after that T 2, or vice versa.

Anomalies: Unrepeatable Reads • Suppose that A is the number of copies available for a book. • Transactions T 1 and T 2 both place an order for this book. First they check the availability of the book. • Consider now the following: 1. T 1 checks whether A is greater than 1. Suppose T 1 sees (reads) value 1. 2. 3. 4. 5. • T 2 also reads A and sees 1. T 2 decrements A to 0. T 2 commits. T 1 tries to decrement A, which is now 0, and gets an error because some integrity check doesn’t allow it. This situation can never arise in a serial execution of T 1 and T 2.

Anomalies: Overwriting uncommitted data • • Suppose that Larry and Harry are two employees, and their salaries must be kept the equal. T 1 sets their salaries to $2000 and T 2 sets their salaries to $1000. Now consider the following schedule: T 1 r(Larry) w(Larry) T 2 r(Harry) w(Harry) r(Larry) w(Larry) commit Unfortunately, Harry will be paid more than Larry.

Summarizing the Terminology • A transaction (model) is a sequence of r and w actions on database elements. • A schedule is a sequence of reads/writes actions performed by a collection of transactions. • Serial Schedule = All actions for each transaction are consecutive. r 1(A); w 1(A); r 1(B); w 1(B); r 2(A); w 2(A); r 2(B); w 2(B); … • Serializable Schedule: A schedule whose “effect” is equivalent to that of some serial schedule. We will introduce a sufficient condition for serializability.

Conflicts • ri(X); rj(Y) ≡ rj(Y); ri(X) – i. e. we can always flip ri(X); rj(Y) (even when X=Y). • We can flip ri(X); wj(Y) as long as X≠Y • However, ri(X); wj (X) wj(X); ri (X) – In the RHS, Ti reads the value of X written by Tj, whereas it is not so in the LHS. • We can flip wi(X); wj(Y); provided X≠Y • However, wi(X); wj(X); wi(X); – The final value of X may be different depending on which write occurs last.

Conflicts (Cont’d) Sumarizing, there is a conflict if one of these two conditions hold. 1. A read and a write of the same X, or 2. Two writes of the same X • • Such actions conflict in general and may not be swapped in order. All other events (reads/writes) may be swapped without changing the effect of the schedule (on the DB). Definition • A schedule is conflict-serializable if it can be converted into a serializable schedule by a series of non conflicting swaps of adjacent elements

Example r 1(A); w 1(A); r 2(A); w 2(A); r 1(B); w 1(B); r 2(B); w 2(B) r 1(A); w 1(A); r 2(A); r 1(B); w 2(A); w 1(B); r 2(B); w 2(B) r 1(A); w 1(A); r 1(B); r 2(A); w 1(B); w 2(A); r 2(B); w 2(B) r 1(A); w 1(A); r 1(B); w 1(B); r 2(A)w 2(A); r 2(B); w 2(B)

Conflict serializability • Sufficient condition for serializability but not necessary. Example S 1: w 1(Y); w 1(X); w 2(Y); w 2(X); w 3(X); This is serial S 2: w 1(Y); w 2(X); w 1(X); w 3(X); • S 2 isn’t conflict serializable, but it is serializable. It has the same effect as S 1. – Intuitively, the values of X written by T 1 and T 2 have no effect, since T 3 overwrites them.

Serializability/precedence Graphs • Non swappable pairs of actions represent potential conflicts between transactions. • The existence of non swappable actions enforces an ordering on the transactions that house these actions. • Nodes: transactions {T 1, …, Tk} • Arcs: There is an arc from Ti to Tj if they have conflict access to the same database element X and Ti is first; in written Ti <S Tj.
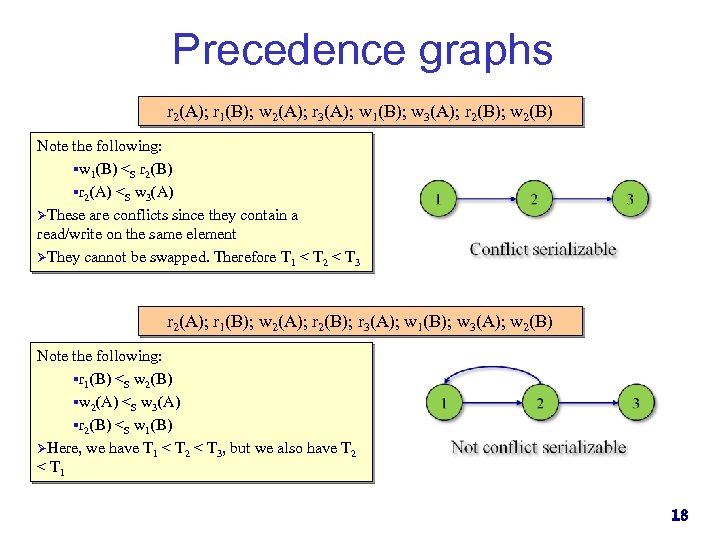
Precedence graphs r 2(A); r 1(B); w 2(A); r 3(A); w 1(B); w 3(A); r 2(B); w 2(B) Note the following: §w 1(B) <S r 2(B) §r 2(A) <S w 3(A) ØThese are conflicts since they contain a read/write on the same element ØThey cannot be swapped. Therefore T 1 < T 2 < T 3 r 2(A); r 1(B); w 2(A); r 2(B); r 3(A); w 1(B); w 3(A); w 2(B) Note the following: §r 1(B) <S w 2(B) §w 2(A) <S w 3(A) §r 2(B) <S w 1(B) ØHere, we have T 1 < T 2 < T 3, but we also have T 2 < T 1 18

• If there is a cycle in the graph – Then, there is no serial schedule which is conflict equivalent to S. • Each arc represents a requirement on the order of transactions in a conflict equivalentserial schedule. • A cycle puts too many requirements on any linear order of transactions. • If there is no cycle in the graph – Then any topological order of the graph suggests a conflict equivalent schedule. • A topological ordering of a directed acyclic graph (DAG) is a linear ordering of its nodes in which each node comes before all nodes to which it has outbound edges.

Why the Precedence Graph Test Works? Idea: if the precedence graph is acyclic, then we can swap actions to form a serial schedule. Given that the precedence graph is acyclic, there exists Ti in S such that there is no Tj in S that Ti depends on. – We swap all actions of Ti to the front (of S). – (Actions of Ti)(Actions of the other n 1 transactions) – The tail is a precedence graph that is the same as the original without Ti, i. e. it has n 1 nodes. – Repeat for the tail.

Schedulers • A scheduler takes requests from transactions for reads and writes, and decides if it is “OK” to allow them to operate on DB or defer them until it is safe to do so. • Ideal: a scheduler forwards a request iff it cannot result in a violation of serializability. – Too hard to decide this in real time. • Real: a scheduler forwards a request if it cannot result in a violation of conflict erializability. s

Lock Actions • Before reading or writing an element X, a transaction Ti requests a lock on X from the scheduler. • The scheduler can either grant the lock to Ti or make Ti wait for the lock. • If granted, Ti should eventually unlock (release) the lock on X. • Shorthands: – li(X) = “transaction Ti requests a lock on X” – ui(X) = “Ti unlocks/releases the lock on X”

Validity of Locks • The use of locks must be proper in 2 senses: – Consistency of Transactions: • Read or write X only when hold a lock on X. – ri(X) or wi(X) must be preceded by some li(X) with no intervening ui(X). • If Ti locks X, Ti must eventually unlock X. – Every li(X) must be followed by ui(X). – Legality of Schedules: • Two transactions may not have locked the same element X without one having first released the lock. – A schedule with li(X) cannot have another lj(X) until ui(X) appears in between.
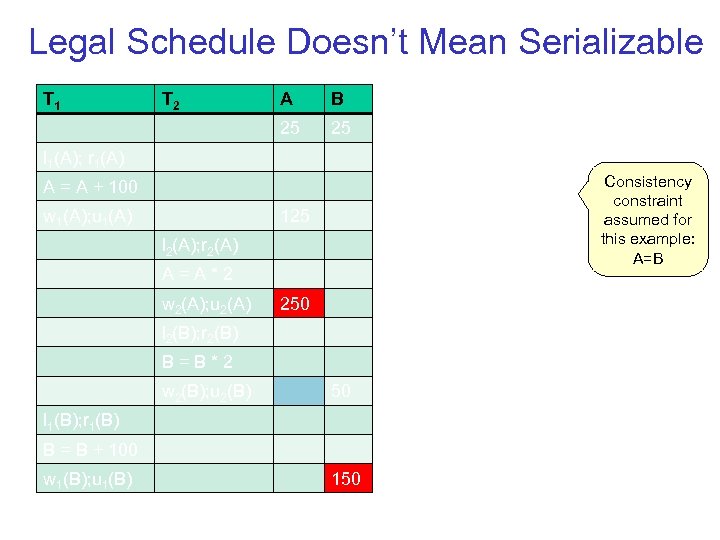
Legal Schedule Doesn’t Mean Serializable T 1 T 2 A B 25 25 l 1(A); r 1(A) Consistency constraint assumed for this example: A=B A = A + 100 w 1(A); u 1(A) 125 l 2(A); r 2(A) A=A*2 w 2(A); u 2(A) 250 l 2(B); r 2(B) B=B*2 w 2(B); u 2(B) 50 l 1(B); r 1(B) B = B + 100 w 1(B); u 1(B) 150
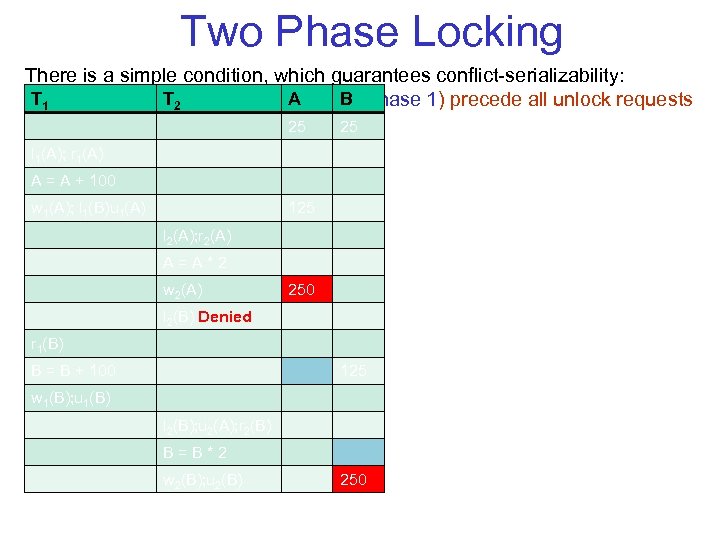
Two Phase Locking There is a simple condition, which guarantees conflict serializability: T T 2 A B In 1 every transaction, all lock requests (phase 1) precede all unlock requests (phase 2). 25 25 l 1(A); r 1(A) A = A + 100 w 1(A); l 1(B)u 1(A) 125 l 2(A); r 2(A) A=A*2 w 2(A) 250 l 2(B) Denied r 1(B) B = B + 100 125 w 1(B); u 1(B) l 2(B); u 2(A); r 2(B) B=B*2 w 2(B); u 2(B) 250

Why 2 PL Works? • Precisely: a legal schedule S of 2 PL transactions is conflict erializable. s • Proof is an induction on n, the number of transactions.

Why 2 PL Works (Cont’d) • Basis: if n=1, then S={T 1}, and hence S is conflict serializable. • Induction: S={T 1, …, Tn}. Find the first transaction, say Ti, to perform an unlock action, say ui(X). We show that the r/w actions of Ti can be moved to the front of the other transactions without conflict. Consider some action such as wi(Y). Can it be preceded by some conflicting action wj(Y) or rj(Y)? In such a case we cannot swap them. – If so, then uj(Y) and li(Y) must intervene, as • • wj(Y). . . uj(Y). . . li(Y). . . wi(Y). – Since Ti is the first to unlock, ui(X) appears before uj(Y). – But then li(Y) appears after ui(X), contradicting 2 PL. • Conclusion: wi(Y) can slide forward in the schedule without conflict; similar argument for a ri(Y) action.

Shared/Exclusive Locks • Problem: while simple locks + 2 PL guarantee conflict erializability, s they do not allow two readers of DB element X at the same time. • But having multiple readers is not a problem for conflict erializability (since read actions commute). s

Shared/Exclusive Locks (Cont’d) • Solution: Two kinds of locks: 1. Shared lock sli(X) allows Ti to read, but not write X. – It prevents other transactions from writing X but not from reading X. 2. Exclusive lock xli(X) allows Ti to read and/or write X; no other transaction may read or write X.

• Consistency of transaction conditions: – A read ri(X) must be preceded by sli(X) or xli(X), with no intervening ui(X). – A write wi(X) must be preceded by xli(X), with no intervening ui(X). • Legal schedules: – No two exclusive locks. • If xli(X) appears in a schedule, then there cannot be a xlj(X) until after a ui(X) appears. – No exclusive and shared locks. • If xli(X) appears, there can be no slj(X) until after ui(X). • If sli(X) appears, there can be no wlj(X) until after ui(X). • 2 PL condition: – No transaction may have a sl(X) or xl(X) after a u(Y).

Scheduler Rules • When there is more than one kind of lock, the scheduler needs a rule that says “if there is already a lock of type A on DB element X, can I grant a lock of type B on X? ” • The compatibility matrix answers the question. Compatibility Matrix for Shared/Exclusive Locks is:

Exercise r 1(A); r 2(B); r 3(C); r 1(B); r 2(C); r 3(D); w 1(A); w 2(B); w 3(C); T 1 xl(A); r 1(A) T 2 T 3 xl(B); r 2(B) xl(C); r 3(C) sl(B) denied sl(C) denied sl(D); r 3(D); ul(D) w 1(A); w 2(B); w 3(C); ul(C) sl(C); r 2(C); ul(B); ul(C) sl(B); r 1(B); ul(A); ul(B)

Upgrading Locks • Instead of taking an exclusive lock immediately, a transaction can take a shared lock on X, read X, and then upgrade the lock to exclusive so that it can write X. Upgrading Locks allows more concurrent operation: Had T 1 asked for an exclusive lock on B before reading B, the request would have been denied, because T 2 already has a shared lock on B.

Exercise r 1(A); r 2(B); r 3(C); r 1(B); r 2(C); r 3(D); w 1(A); w 2(B); w 3(C); T 1 sl(A); r 1(A) T 2 T 3 sl(B); r 2(B) sl(C); r 3(C) sl(B); r 1(B) sl(C); r 2(C) sl(D); r 3(D) xl(A); w 1(A); ul(B) xl(B); w 2(B); ul(C) xl(C); w 3(C); ul(D)

Possibility for Deadlocks Example: T 1 and T 2 each reads X and later writes X. Problem: when we allow upgrades, it is easy to get into a deadlock situation.

Solution: Update Locks • • • Update lock uli(X). – Only an update lock (not shared lock) can be upgraded to exclusive lock (if there are no shared locks anymore). – A transaction that will read and later on write some element A, asks initially for an update lock on A, and then asks for an exclusive lock on A. Such transaction doesn’t ask for a shared lock on A. Legal schedules: – read action permitted when there is either a shared or update lock. – An update lock can be granted while there is a shared lock, but the scheduler will not grant a shared lock when there is an update lock. 2 PL condition: No transaction may have an sl(X), ul(X) or xl(X) after a u(Y).

Example T 1 sl(A); r(A) T 2 T 3 ul(A); r(A) sl(A) Denied xl(A) Denied u(A) xl(A); w(A) u(A) sl(A); r(A) u(A)

(No) Deadlock Example T 1 and T 2 each read X and later write X. Deadlock when using sl and xl locks only. Fine when using update locks.

Exercise r 1(A); r 2(B); r 3(C); r 1(B); r 2(C); r 3(D); w 1(A); w 2(B); w 3(C); T 1 ul(A); r 1(A) T 2 T 3 ul(B); r 2(B) ul(C); r 3(C) sl(B) denied sl(C) denied sl(D); r 3(D); xl(A); w 1(A); xl(B); w 2(B); xl(C); w 3(C); ul(D); ul(C) sl(C); r 2(C); ul(B); ul(C) sl(B); r 1(B); ul(A); ul(B)

Benefits of Upgrade Locks T 1 T 2 T 3 T 4 T 5 T 6 T 7 T 8 T 9 s(A); r(A) u(A); r(A) s(A); denied u(A) xl(A); w(A) u(A) s(A); r(A)

What should we lock? • The whole table or just single rows? What’s database object? What should be the locking granularity? SELECT min(year) FROM Movies; • What happens if we insert a new tuple with the smallest year? • Phantom problem: A transaction retrieves a collection of tuples twice and sees different results, even though it doesn’t modify those tuples itself.

Transaction support in SQL • SET TRANSACTION ISOLATION LEVEL X – Where X can be • SERIALIZABLE (Default) • REPEATABLE READ • READ COMMITED • READ UNCOMMITED With a scheduler based on locks: • A SERIALIZABLE transaction obtains locks before reading and writing objects, including locks on sets (e. g. table) of objects that it requires to be unchangeable and holds them until the end, according to 2 PL. • A REPEATABLE READ transaction sets the same locks as a SERIALIZABLE transaction, except that it doesn’t lock sets of objects, but only individual objects.

Transaction support in SQL • • A READ COMMITED transaction T obtains exclusive locks before writing objects and keeps them until the end. However, it obtains shared locks before reading values and then immediately releases them; their effect is to ensure that the transaction that last modified the values is complete. Thus, 1. T reads only the changes made by committed transactions. 2. No value written by T is changed by any other transaction until T is completed. 3. However, a value read by T may well be modified by another transaction (which eventually commits) while T is still in progress. 4. T is also exposed to the phantom problem. A READ UNCOMMITED transaction doesn’t obtain any shared lock at all. So, it can read data that is being modified. Such transactions are allowed to be READ ONLY only. So, such transaction doesn’t ask for any lock at all.
In Summary Level READ UNCOMMITED READ COMMITTED REPEATABLE READ SERIALIZABLE Reading Uncommited Data (Dirty Read) Unrepeatable Read Phantom
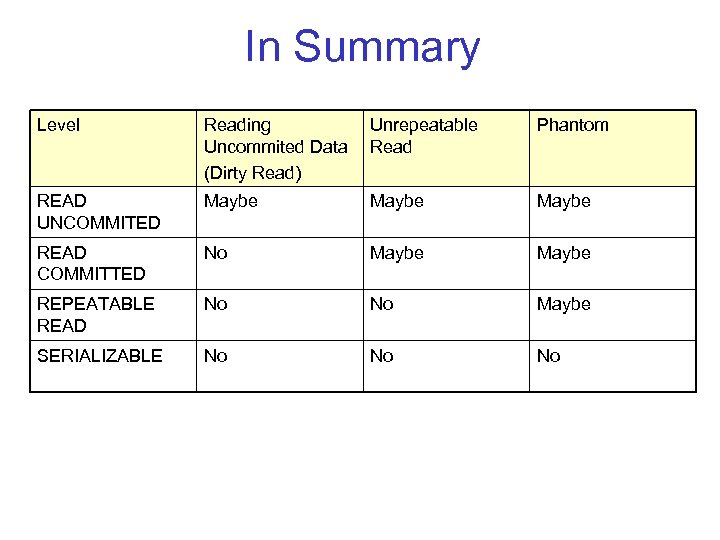
In Summary Level Reading Uncommited Data (Dirty Read) Unrepeatable Read Phantom READ UNCOMMITED Maybe READ COMMITTED No Maybe REPEATABLE READ No No Maybe SERIALIZABLE No No No
234915a9d7b1d6513af36119f1da7712.ppt