TOWARDS VIRTUAL TRY-ON TECHNOLOGY André Gagalowicz Projet MIRAGES

TOWARDS VIRTUAL TRY-ON TECHNOLOGY André Gagalowicz Projet MIRAGES INRIA - Rocquencourt - Domaine de Voluceau 78153 Le Chesnay Cedex E-Mail : Andre. Gagalowicz@inria. fr Tél : 01 39 63 54 08

TABLE OF CONTENTS I. INTRODUCTION II. CONTEXT II. 1. Input II. 2. Output III. SIMULATION PROCESS III. 1. Numerical model for textile material III. 2. Scene creation III. 3. Evolution of the system over time IV. RESULTS V. CONCLUSION

I. INTRODUCTION Aim : Commercial software in order to buy garments through internet Presentation restricted to the case of WOVEN textiles Limitation to a planar surface approach

APPLICATION: VIRTUAL TRY-ON (+ VIRTUAL PROTOTYPING) FUNDING: Big Contract from ANR RNTL (french government) for 3 years started in April 2007 Partners: - TEMAT INDUSTRIES (3 D scanner SYMCAD) - LA REDOUTE (biggest French garment distributor) - Nadina Corrado (Fashion designer) - ENSITM (French Institute specialist of the mechanics of textile) - INRIA (MIRAGES project; specialist in garment simulation) Target: produce a first prototype

Textiles have a NONLINEAR Behaviour HYSTERETIC

TENSION F e

SHEAR F q

BENDING M K

II. CONTEXT II. 1 Input

III. 1 Numerical model for textile material a) Classical mass/spring model (finite elements)

II. CONTEXT II. 2 Output Evolution of the system over time - 3 D data - images

III. SIMULATION PROCESS III. 1 Numerical model for textile materials III. 2 Creation of the scene III. 3 Evolution of the system over time

III. 1 Numerical Model for Textile Material (continued) b) Improved mass/spring model • Warp/Weft structure is preserved • Mixture of bipolar springs (tension and shear) and quadripolar (angular) springs

III. 1 Numerical model for textile material (continued) c) 2 D pattern Meshing Industrial representation of 2 D patterns

III. 2 Creation of the scene III. 2. 1. Scene description

III. 2. 2. Garment Confection a) 2 D patterns positioned AUTOMATICALLY around the numerical mannequin b) Sewing of 2 D patterns c) Gravity is added

III-2 -2 a: Automatic prepositioning of the garment CRUCIAL for the application and VERY DIFFICULT Our solution solves the problem GEOMETRICALLY The 3 D garment appears sewn around the body and with a very small amount of spring deformations (. 001 mm of average deformation) The simulator is only used for the final tuning (tremendous reduction of the computing time)

How is it done ? THE 3 D MANNEQUIN Hypothesis : • The body is standing • The body has his legs and arms put apart symmetrically

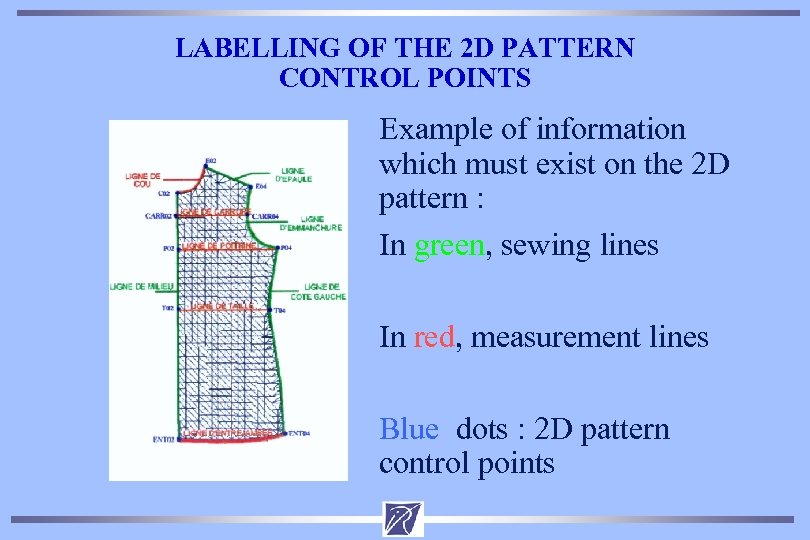LABELLING OF THE 2 D PATTERN CONTROL POINTS Example of information which must exist on the 2 D pattern : In green, sewing lines In red, measurement lines Blue dots : 2 D pattern control points

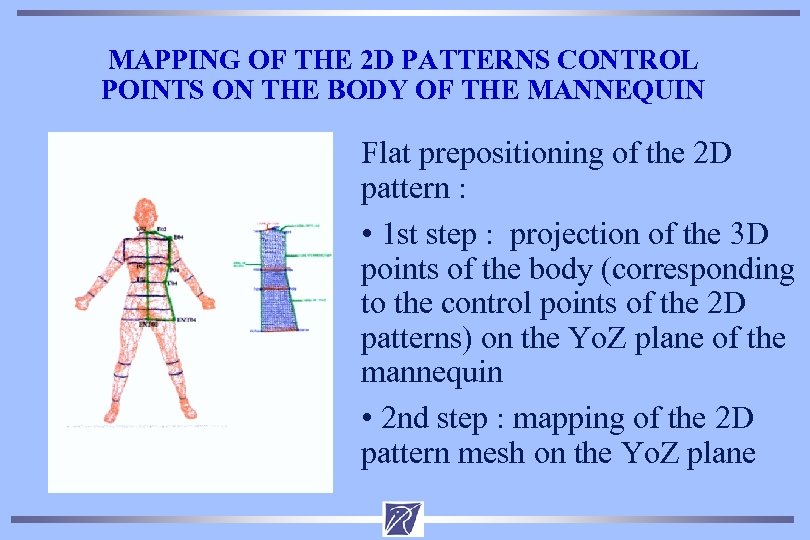MAPPING OF THE 2 D PATTERNS CONTROL POINTS ON THE BODY OF THE MANNEQUIN Flat prepositioning of the 2 D pattern : • 1 st step : projection of the 3 D points of the body (corresponding to the control points of the 2 D patterns) on the Yo. Z plane of the mannequin • 2 nd step : mapping of the 2 D pattern mesh on the Yo. Z plane

III. 2. 2. b 2 D pattern sewing 2 D patterns are sewn along sewing edges Remark : Ambiguïty of the sewing information on the pattern !

III. 2. 3. Blowing of the Garment around the body

III. 3. Evolution of the system over time III. 3. 1. Integration of the law of dynamics III. 3. 2. Control of the nonlinearity, the viscosity model and of the hysteresis III. 3. 3. Spatial coherence maintenance

III. 3. 1 Integration of the law of dynamics • Fondamental law of dynamics SF • • ext = m. A + c v Implicit integration method (Baraff) viscosity parameters measured from real textile

III. 3. 2 Control of the nonlinearity and of the hysteresis • Nonlinear and hysteretical springs control the KES of textile • Validation by simulating Kawabata tests

RESULTS ON THE CONTROL OF THE KES INSURE THAT OUR MECHANICAL MODEL MIMICS PRECISELY REAL WARP/WEFT TEXTILE DOES NOT CONTROL COMPRESSION

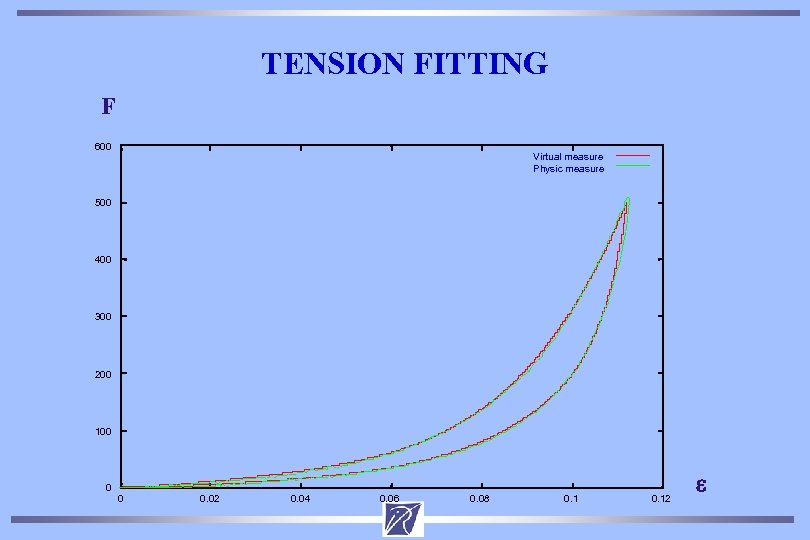TENSION FITTING F 600 Virtual measure Physic measure 500 400 300 200 100 0 0 0. 02 0. 04 0. 06 0. 08 0. 12 e

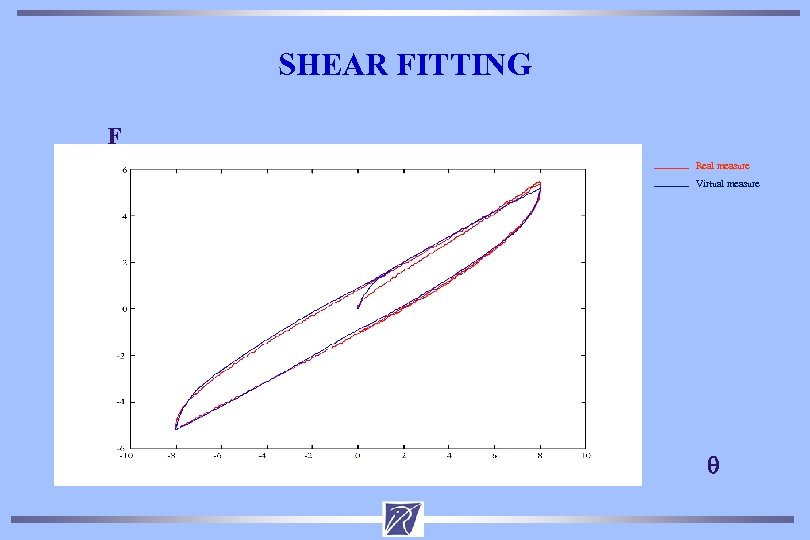SHEAR FITTING F Real measure Virtual measure q

BENDING FITTING M K

EXPERIMENTAL DETERMINATION OF DAMPING PARAMETERS in THE EQUATION OF DYNAMICS: c. V AIM: obtain a total phisical control of the equation of dynamics

Damping model (Rayleigh) F = ( M + K) V • M : mass matrix • K : stiffness matrix and have never been computed precisely before.

Rayleigh’s damping model applied for fabric model 3 spring types => 3 stiffness matrices K. K = Kbnd + Ksh + Ktns Bending Shearing Tensile Rayleigh's Model => Fdamp=( M+ bnd Kbnd+ sh Ksh+ tns Ktns) V

Identification of Rayleigh’s model parameters(1)

Identification of Rayleigh’s model parameters(2)

Real fall down

Global Minimization Ferror=MA-MG-Fsprings-Fdamp Minimizing ||Ferror || by differentiating Linear system : A ( bnd sh tns)T =b Numerically A is ill-conditioned => the solution is not stable Use of an iterative minimization algorithm

RESULT: Comparison between the real and the virtual FREE-FALL in the VISCOUS part of the trajectory

III. 3. 3 Spatial coherence maintenance • Detection of collisions • Response to collisions (done implicitly by the integration scheme)

Detection of Collisions • Optimisation through the use of bounding boxes • Use of buckets

Response to Collisions: collision avoided IMPLICITELY (BARAFF method)

Implementation • SGI 02 Unix Workstation • C++ • Tcl scripts for the scene configuration and kinematics

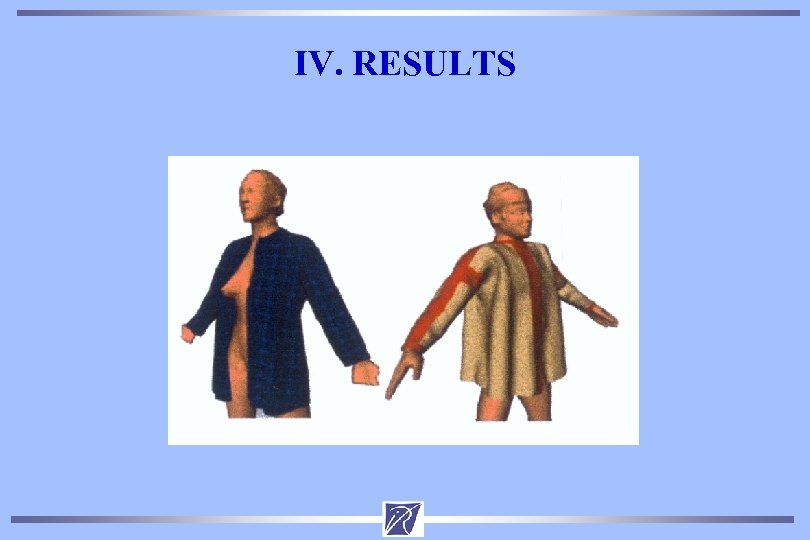IV. RESULTS

V. CONCLUSION Numerous soft objects have the same behaviour as textiles Example : Muscular tissues, … Extension to the volumetric case is STRAIGHTFORWARD but requires HEAVY computations actually

SOME SIMULATION RESULTS

CONTINUED

BUCKLING MODELING

STUDY OF BUCKLING (REAL)

STUDY OF BUCKLING (SIMULATED)