e515b41a04afe3b00acee8b394275762.ppt
- Количество слайдов: 22

Towards Value Disclosure Analysis in Modeling General Databases Xintao Wu Songtao Guo Yingjiu Li UNC Charlotte Singapore Management Univ SAC’ 06 April 23 -27, 2006, Dijon, France

Outline p p p Motivation General Location Model Value Disclosure Analysis n n n p Basic disclosure scenario Conditional disclosure scenario Combinatorial disclosure scenario Conclusion and Future Work SAC, Dijon, France April 23 -27, 2006 2

Motivation p Information Disclosure in general databases Identity Disclosure SSN Name Value Disclosure Zip Race 1 28223 Asian 20 2 28223 Asian 3 28262 n SAC, Dijon, France 28223 Dividends Wages Interests M 10 k 85 k 2 k 30 F 15 k 70 k 18 k Black 20 M 50 k 120 k 35 k . . Age Sex . . . Asian 20 M 80 k 110 k 15 k April 23 -27, 2006 3

Motivation p Previous work n Additive randomization approach p p p n Multiplicative rotation approach p p n Chen et al. ICDM 05 Kargupta et al. TKDE 06 Limitation p p p Agrawal & Srikant, SIGMOD 00, Agrawal &Aggawal PODS 01 Kargupta et al. ICDM 03, Du et al. SIGMOD 05 Various methods from statistical databases Conduct disclosure analysis on the data space Prune to potential attacking Our Modeling based approach n n n First build an approximate statistical model Analyze disclosure on the parameter space Apply the model to generate data for future mining SAC, Dijon, France April 23 -27, 2006 4

Application p Database Application Testing on the local development databases p p n a small number of data samples cannot conduct performance testing Testing against the live production databases p privacy disclosure incorrectly update the underlying databases. Generate mock databases for application software testing such that the generated data n n n Valid Resembling to original data in terms of statistical distribution Privacy preserving SAC, Dijon, France April 23 -27, 2006 5
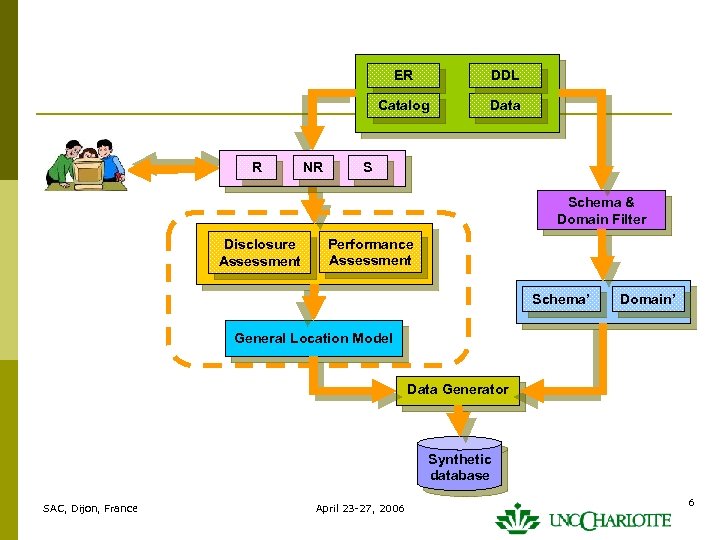
ER Catalog R NR DDL Data S Schema & Domain Filter Disclosure Assessment Performance Assessment Schema’ Domain’ General Location Model Data Generator Synthetic database SAC, Dijon, France April 23 -27, 2006 6
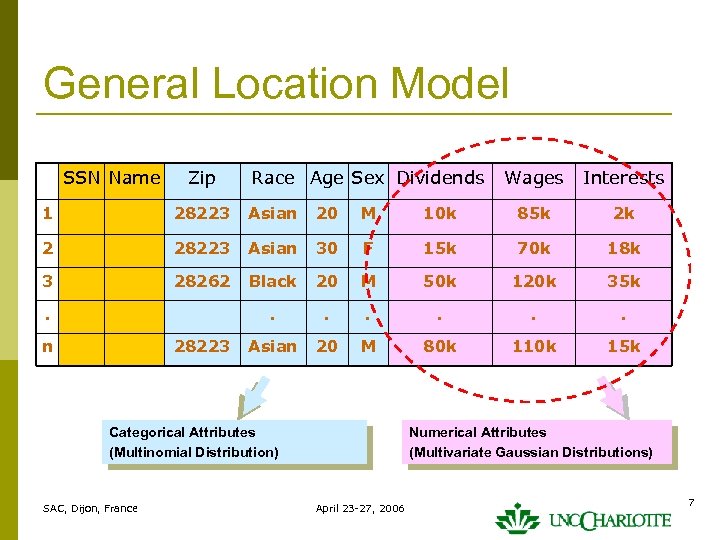
General Location Model SSN Name Zip Race Age Sex Dividends Wages Interests 1 28223 Asian 20 M 10 k 85 k 2 k 2 28223 Asian 30 F 15 k 70 k 18 k 3 28262 Black 20 M 50 k 120 k 35 k . . . Asian 20 M 80 k 110 k 15 k . n 28223 Categorical Attributes (Multinomial Distribution) SAC, Dijon, France Numerical Attributes (Multivariate Gaussian Distributions) April 23 -27, 2006 7

General Location Model p Given a dataset which contains n tuples n Categorical attributes: n Numerical attributes: p The categorical part can be summarized by a contingency table with cells. The number of tuples in each cell, has a multinomial distribution p For each cell d, the numerical attributes satisfy a conditionally multivariate normal distribution SAC, Dijon, France April 23 -27, 2006 8

Parameter Fitting p The MLE estimates of parameter where SAC, Dijon, France as follows is the set of tuples belonging to cell d April 23 -27, 2006 9

Value Disclosure p Attackers may be able to estimate or infer the value of a certain confidential numerical attribute of an entity or a group of entities with a level of accuracy than a threshold p All numerical attribute values are generated from multivariate normal distribution, specifically from SSN Name Zip Race Age Sex Dividends Wages Interests 28262 30 M … … … . . 28262 Asian 30 M 28223 White 50 F … … 28223 SAC, Dijon, France Asian White 50 F April 23 -27, 2006 10

Value Disclosure Analysis n Basic Disclosure Scenario p p p n Conditional Scenario p n All numerical attributes are confidential The analysis is based on probability density contour. The disclosure is measured in terms of confidence interval or confidence region. Non-confidential + confidential attributes Combinatorial Scenario p Linear combinations exist among both confidential and non-confidential attributes SAC, Dijon, France April 23 -27, 2006 11

Privacy Measure n Confidence Interval p p n Agrawal & Srikant SIGMOD 00 If the original value can be estimated with c% confidence to lie in the interval [a, b], then the interval width (b-a) defines the amount of privacy at c% confidence level Confidence Region p In the p-dimensional case, a c% confidence region is determined by the probability density contour of data. SAC, Dijon, France April 23 -27, 2006 12

Basic Disclosure Scenario n Confidential attributes (X) ~ N(μ, Σ) n The projection of this multidimensional ellipsoid on axis zi has bounds: SAC, Dijon, France April 23 -27, 2006 13

Basic Disclosure Scenario n Measure Privacy p Heuristic method § Use a hyper-rectangle to approximate the ellipsoid § Measure privacy for one dimension p n Adjust parameters Original Interval SAC, Dijon, France Dissimilarity Constrain (d) New Interval April 23 -27, 2006 14

Conditional Scenario p Confidential attributes (X) and Non-confidential attributes (S) n E. g. , the non-confidential values of Dividends and Wages can help predict confidential values of Interests n Same method with conditional Parameters: SAC, Dijon, France April 23 -27, 2006 15

Combinatorial Scenario Race Age Sex Dividends Asian Black 20 30 20 M F M 10 k 15 k 50 k Wages Interests 85 k 70 k 120 k 2 k 18 k 35 k Total Income 87 k 103 k 205 k • Many Potential Combinations exist, e. g. Dividends + Wages + Interests = Total Income • Even if the level of security provided for a single confidential attribute is adequate, the level of security provided for linear combinations of confidential attributes could be very low. SAC, Dijon, France April 23 -27, 2006 16

Combinatorial Scenario p Canonical Correlation Analysis (CCA) n A statistical procedure that is used to identify and quantify the relationship between two sets of variables, S and X. n CCA can identify a linear combination of variables in one set , X, that have the highest correlation with a linear combination of variables in another set, S. n It can be used to evaluate the level of security when estimating the linear combinations of the confidential attributes, X, using the non-confidential attributes, S. SAC, Dijon, France April 23 -27, 2006 17

Combinatorial Scenario p Canonical Correlation Analysis (CCA) n λ 1 : represents the most general measure of inferential value disclosure for any combination 1− λ 1 : the worst-case security n λ 1 ≤λ : no combinatorial disclosure exists Adjust parameters n If λi > λ then λi = λ, keeping other eigenvalues, eigenvectors unchanged. Get a new n Adjust : optimization problem n p SAC, Dijon, France April 23 -27, 2006 18

Conclusion p Propose a model-based privacy preserving approach p Investigate value disclosure in three scenarios SAC, Dijon, France April 23 -27, 2006 19

Future Work p How to conduct individual value disclosure analysis when individual privacy intervals are specified p How the information loss due to modeling affects the utility of generated data SAC, Dijon, France April 23 -27, 2006 20

Acknowledgement p NSF Grant n n p Personnel n n p CCR-0310974 IIS-0546027 Xintao Wu, Songtao Guo, UNC Charlotte Yingjiu Li, Singapore Management Univ. More Info n n http: //www. cs. uncc. edu/~xwu/ xwu@uncc. edu, SAC, Dijon, France April 23 -27, 2006 21

Questions? Thank you! SAC, Dijon, France April 23 -27, 2006 22
e515b41a04afe3b00acee8b394275762.ppt