Towards A Formalization Of Teamwork With Resource Constraints

Towards A Formalization Of Teamwork With Resource Constraints Praveen Paruchuri, Milind Tambe, Fernando Ordonez University of Southern California Sarit Kraus Bar-Ilan University, Israel University of Maryland, College Park December, 2003 University of Southern California 1

Motivation: Teamwork with Resource Constraints Agent teams: Agents maximize team rewards and also ensure limited resource consumption E. g. , Limited communication bandwidth, limited battery power etc Example Domain: Sensor Net Agents - Limited replenishable energy Mars Rovers - Limited energy for each daily activity University of Southern California 2

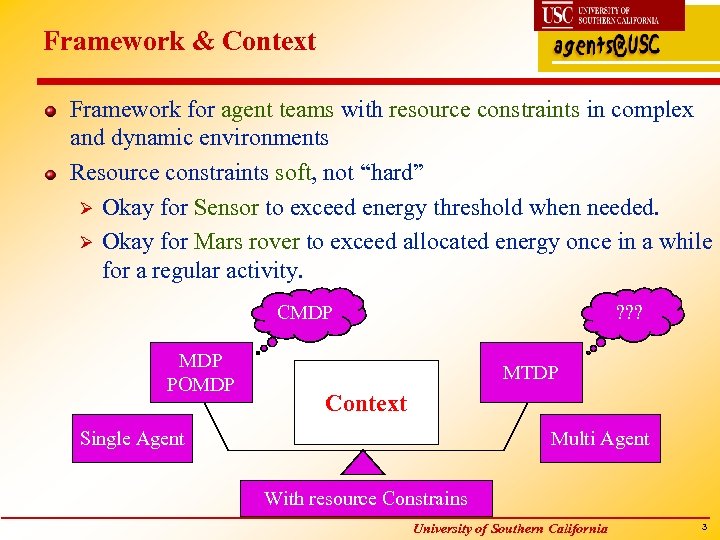Framework & Context Framework for agent teams with resource constraints in complex and dynamic environments Resource constraints soft, not “hard” Ø Okay for Sensor to exceed energy threshold when needed. Ø Okay for Mars rover to exceed allocated energy once in a while for a regular activity. CMDP POMDP ? ? ? MTDP Context Single Agent Multi Agent With resource Constrains University of Southern California 3

Our Contributions Extended MTDP ( EMTP ) – A Distributed MDP framework Bound Expected Resource Consumption Maximize Expected Team Reward EMTDP ≠ CMDP with many agents. Ø Policy Randomization in CMDP – Causes miscoordination in teams. Ø Algorithm for transforming conjoined EMTDP (initial formulation dealing with joint actions) into actual EMTDP (reasoning about individual actions). Proof of equivalence between different transformations. Solution algorithm for the actual EMTDP. University of Southern California 4

E-MTDP: Formally Defined An E-MTDP (for a 2 agent case) is a tuple where, Ø S, A, P, R : As defined in MTDP. Ø C 1 = [ ]: Vector of cost of resource k for joint action a in state i ( for agent 1). Ø T 1 = [ ]: Threshold on expected resource k consumption. Ø N =[ ]: Vector of joint communication costs for joint action a in state i. Ø Q : Threshold on communication costs Simplifying assumptions: Ø Individual observability (no POMDPs) Ø Two agents University of Southern California 5

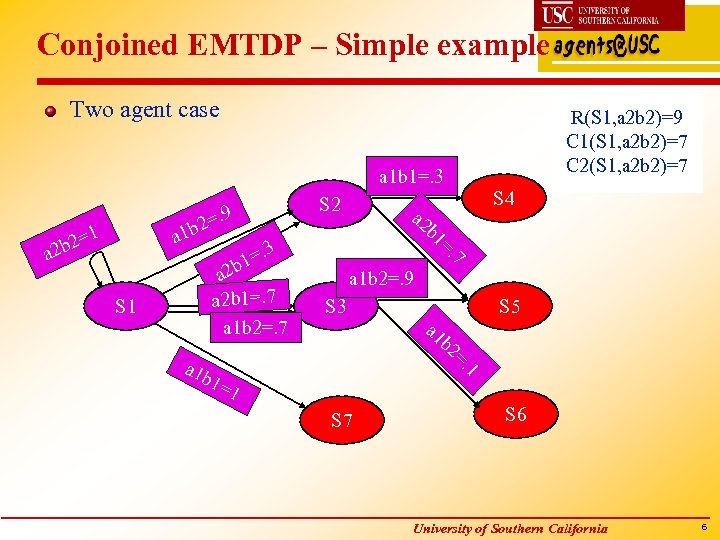Conjoined EMTDP – Simple example Two agent case R(S 1, a 2 b 2)=9 C 1(S 1, a 2 b 2)=7 C 2(S 1, a 2 b 2)=7 a 1 b 1=. 3 9 . b 2= a 1 2=1 a 2 b S 2 a 2 b 1=. 7 a 1 b 2=. 7 a 2 b 1=. 7 . 3 1= a 2 b S 1 S 4 a 1 b 2=. 9 S 3 a 1 b S 5 2=. 1 a 1 b 1=1 S 7 S 6 University of Southern California 6

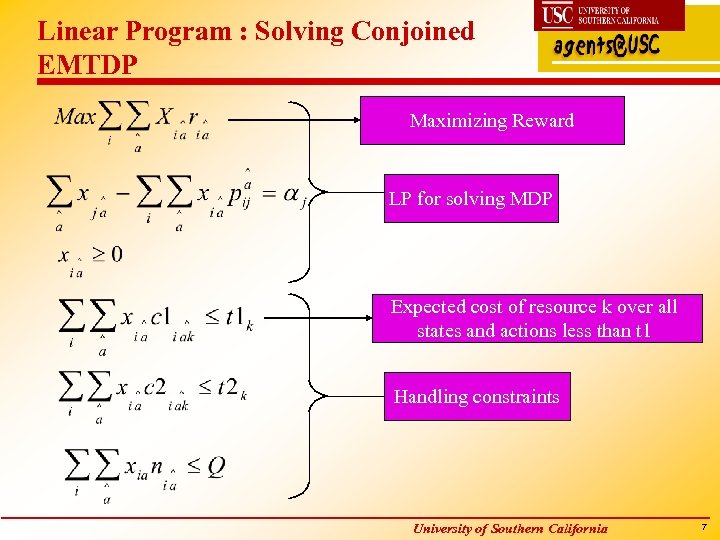Linear Program : Solving Conjoined EMTDP Maximizing Reward LP for solving MDP Expected cost of resource k over all states and actions less than t 1 Handling constraints University of Southern California 7

Sample LP solution VISITED( X 11) VISITED( X 12) VISITED( X 13) VISITED( X 14) 0. 000000 0. 3653846 0. 6346154 0. 000000 a 1 b 1 to be executed 0% time a 1 b 2 : 36% = 9/25 a 2 b 1 : 64% = 16/25 a 2 b 2 : 0% B 1(16/25) B 2(9/25) a 1( 9/25) 144/625 =. 23 81/625 =. 13 a 2(16/25) 256/625 =. 4 Should have been 0. (Miscoordination) 144/625 =. 23 University of Southern California 8

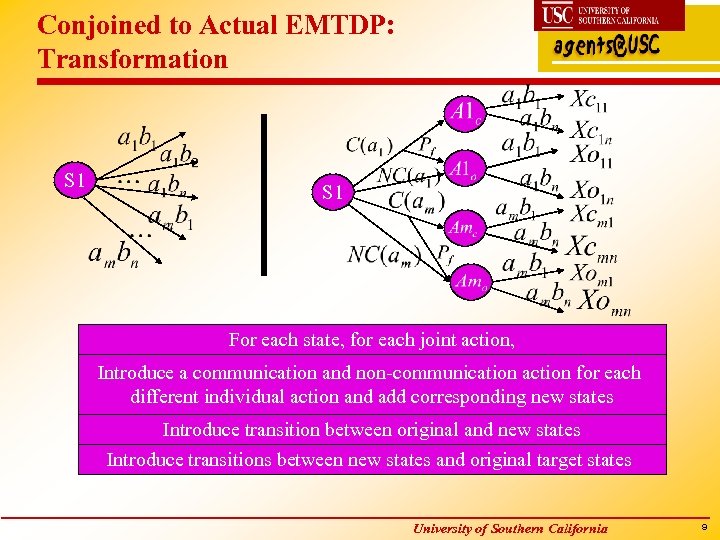Conjoined to Actual EMTDP: Transformation S 1 For each state, for each joint action, Introduce a communication and non-communication action for each different individual action and add corresponding new states Introduce transition between original and new states Introduce transitions between new states and original target states University of Southern California 9

Non-linear Constraints Need to introduce non-linear constraints For each original state Ø For each new state introduced by no communication action – Set conditional probability of corresponding actions equal Ex: P(b 1/ ) = P(b 1/ )=……=P(b 1/ ) && ……. . && P(bn/ ) = P(bn/ )=……=P(bn/ ). , , - Observable, Reached by Comm action - Unobservable, No Comm action University of Southern California 10

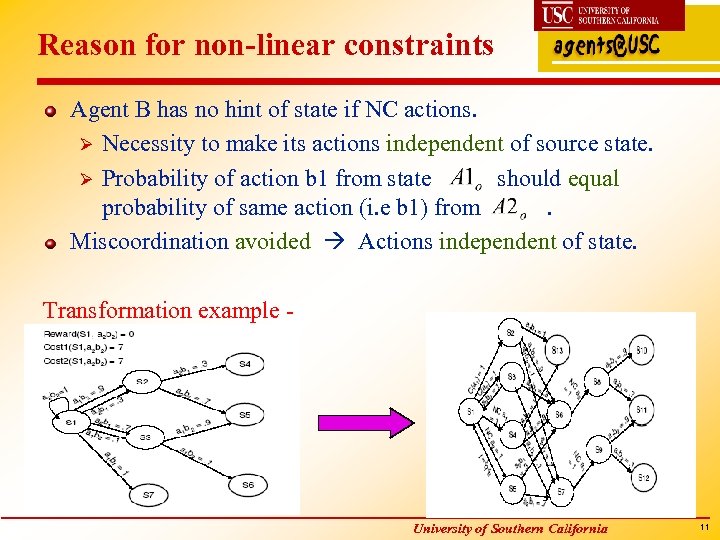Reason for non-linear constraints Agent B has no hint of state if NC actions. Ø Necessity to make its actions independent of source state. Ø Probability of action b 1 from state should equal probability of same action (i. e b 1) from. Miscoordination avoided Actions independent of state. Transformation example - University of Southern California 11

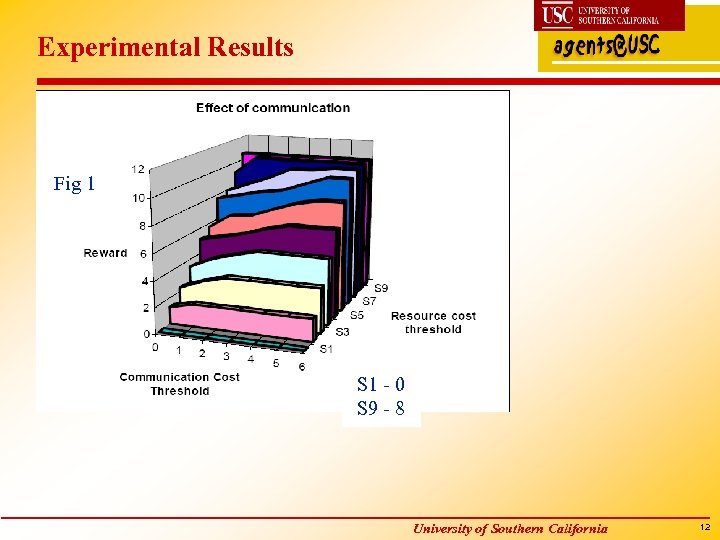Experimental Results Fig 1 S 1 - 0 S 9 - 8 University of Southern California 12

Experiments : Example domain 2 Domain 1: Comparing Expected rewards – Comm Threshold Conjoined Deterministic Miscoordination EMTDP 0 10. 55 0 No reward 6. 99 3 10. 55 0 No 8. 91 6 10. 55 0 No 10. 55 ( Miscoordination resulted in violating resource constraints ) Domain 2 A team of two rovers and several scientists using them Each scientist has a daily routine of observations Rover can use a limited amount of energy in serving a scientist Experiment conducted: Observe Martian rocks Rovers Maximize observation output within the energy budget provided. Soft constraint – Exceeding energy budget on a day is not catastrophic Overutilizing frequently affects other scientist’s work Uncertainty – Only. 75 chance of succeeding in an observation EMTDP had about 180 states, 1500 variables and 40 non-linear constraints. Could handle problem of this order in below 20 secs. University of Southern California 13

Summary and Future Work Novel formalization of teamwork with resource constraints Maximize expected team reward but bound expected resource consumption. Provided a EMTDP formulation where agents avoid miscoordination even though randomized policies. Proved equivalence of different EMTDP transformation strategies ( see paper for details ) Introduction of non-linear constraints. Future Work Ø Need to fix on complexity. Ø Experiment on n-agent case. Ø Extend work to partially observable domains. University of Southern California 14

Thank You Any Questions ? ? ? University of Southern California 15