Tough Modeling System 1 Бурков Денис 11 -1

Tough Modeling System 1 Бурков Денис 11 -1 класс Марчукова Татьяна 11 -3 класс Николаенко Валерия 11 -3 класс Тимофеев Антон 10 -1 класс Научный руководитель: Галинский Виталий Александрович, Преподаватель информатики и программирования ФМЛ № 30 3/15/2018 Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 2 Составные части проекта • Low level: взаимодействие с низкоуровневым API – Microsoft Direct. X (9. 0) • Иерархическое многоуровневое моделирование • Процедурная анимация • Спецэффекты • Анимационное моделирование • Физическое моделирование Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 3 Низкий уровень • • • Взаимодействие с API Microsoft Direct X (9. 0) Задание базовых примитивов Использование аппаратной буферизации Мультитекстурирование Оптимизация вывода примитивов Оптимизация избыточных вызовов смены состояний • Оптимизация конвейера вывода Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

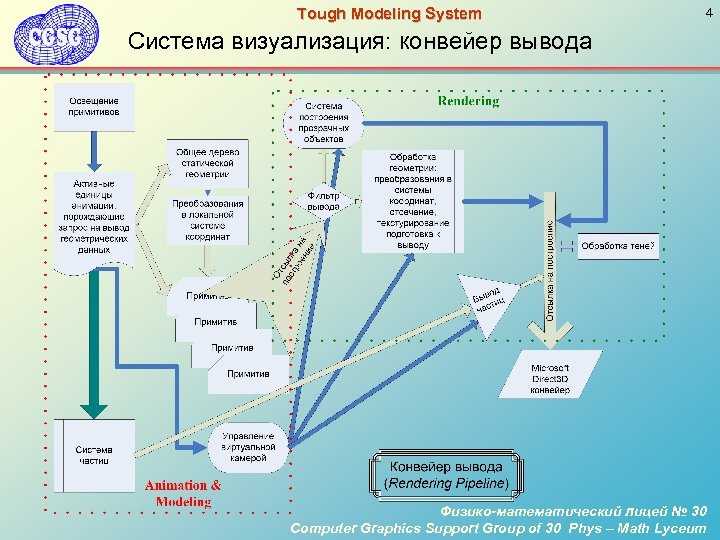
Tough Modeling System 4 Система визуализация: конвейер вывода Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 5 Прозрачные объекты § § Вывод прозрачных объектов связан с определенными трудностями, потому что через них видно предметы, находящиеся позади них Нами разработан алгоритм, позволяющий решить проблему “отложенного” отображения прозрачных объектов для динамической системы реального времени Описание алгоритма Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 6 Вывод текста Демонстрация вывода строки ‘CG’ Пример текстуры шрифта courier и arial Текстурные координаты для символа ’С’ вычисляются следующим образом (здесь: Vertices — массив вершин четырехугольника, поле Tex — текстурные координаты): LY = (INT)((BYTE)C / 16. 0); LY /= 16. 0; LX = ((BYTE)C % 16) / 16. 0; /* 0. 0625 – 1 / 16. 0 – размер одной буквы в текстуре */ Vertices[0]. Tex. U = LX; Vertices[0]. Tex. V = LY + 0. 0625; Vertices[1]. Tex. U = LX; Vertices[1]. Tex. V = LY; Vertices[2]. Tex. U = LX + 0. 0625; Vertices[2]. Tex. V = LY + 0. 0625; Vertices[3]. Tex. U = LX + 0. 0625; Vertices[3]. Tex. V = LY; Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 7 Иерархическое моделирование • Представление сцен в виде дерева объектов. Каждый узел содержит: § Набор геометрических примитивов § Собственную систему координат § Относительную систему координат перехода к узлу верхнего уровня § Параметры вывода Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 8 Процедурная анимация § Объекты (единицы анимации) § Методы (реагирования и отображения) § Синхронизация по времени (с помощью § Функции Win. API Querry. Perfomance. Counter ) Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 9 Прикладные задачи • • • Эффекты на основе частиц Нахождение столкновений Оптические спецэффекты Анимационное моделирование Физическое моделирование Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 10 Оптические спецэффекты § Блики на камере (Lens Flares) § Отражение (на буфере шаблона (Stencil Buffer) ) § Тени (на основе построения области затенения(shadow volume) с использованием буфера шаблона) Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 11 Блики на камере (Lens Flares) § Алгоритм вывода ореолов: Max. Size = COM_MIN(Высота_экрана, Ширина_экрана); Light. In. Cam = Позиция_источника_света – Позиция_камеры; HW = Ширина_экрана / 2. 0; HH = Высота_экрана / 2. 0; for (i = 0; i < Количество_ореолов; i++) { Sc = Размер_ореола * 2 * Max. Size; Вывод_примитива(В_системе_координат_эк рана, Матрица. Масштабирования(4 * Max. Size * Размер_i-го_ореола, 1) * Матрица. Переноса(HW + Light. In. Cam. X * Относительное_расположение_i-го ореола Sc, HH – Light. In. Cam. Y * Относительное_расположение_i-го ореола Sc, 0), Примитив_i-го_ореола); } Текстура бликов Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 12 Вывод теней и отражений Вывод теней основан на построении области затенения (shadow-volume), части пространства, в которой находится тень. Основу алгоритма вывода теней и отражений составляет идея использования буфера шаблона (stencil buffer), который позволяет на аппаратном уровне регистрировать процесс вывода примитивов на экран, а также сравнивать его значения с эталонным для запрета/разрешения последующего построения. Алгоритм вывода теней Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 13 Нахождение столкновений § Алгоритм пересечения с луча со сценой: § 1) Разбиение сцены на voxels; § 2) Нахождение пересечения с ближайшим voxel’ем и установление перехода от одного voxel’а к другому (адаптированный итерационный алгоритм Брезенхема (Bresenham)); § 3) Пересечение со всеми треугольниками данного voxel’а; если ни с кем не пересеклись, то переходим к следующему. Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 14 Разбиение сцены на voxels § Треугольник добавляется к voxel’ю, если выполнится хотя бы один из перечисленных пунктов: - все три вершины внутри вокселя - какое-либо ребро вокселя пересекает треугольник - какое-либо ребро треугольника пересекает воксель Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 15 Эффекты на основе системы частиц Взрыв: Снег: Пример использования двух источников: Снег реализуется одним источником, центр взрыва и дым порождающим частицы в горизонтальной плоскост Обработка каждого источника включает: - Определение количества новых частиц - Инициализация параметров новых частиц - Удаление старых частиц - Изменение параметров и положения активных частиц - Разворот частиц в плоскость камеры. Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 16 Анимационное моделирование • Инверсная кинематика • Деформация свободных форм (Free From Deformation) • Моделирование поведения кожи Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

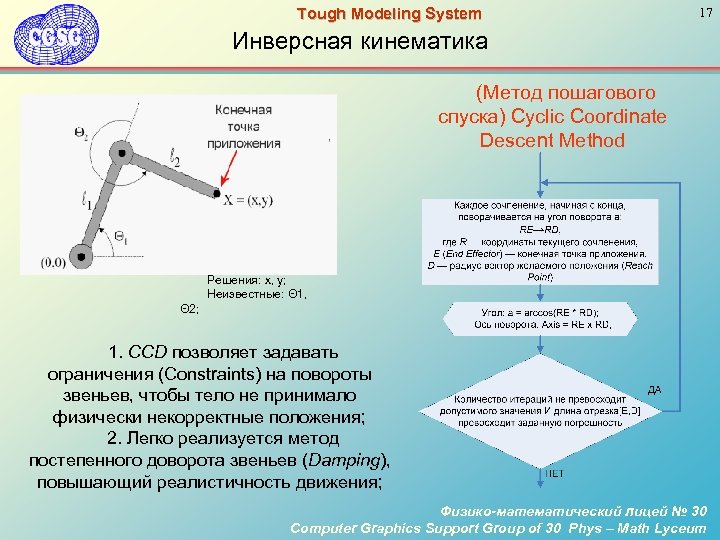
Tough Modeling System 17 Инверсная кинематика (Метод пошагового спуска) Cyclic Coordinate Descent Method Решения: x, y; Неизвестные: Θ 1, Θ 2; 1. CCD позволяет задавать ограничения (Constraints) на повороты звеньев, чтобы тело не принимало физически некорректные положения; 2. Легко реализуется метод постепенного доворота звеньев (Damping), повышающий реалистичность движения; Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 18 Метод пошагового спуска (Cyclic Coordinate Descent Method) Этапы поворота сочленений 1. 3. 2. 4. Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 19 Деформация свободных форм (Free Form Deformation) — Опорные точки куба. — Начальное положение точки. Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 20 Моделирование поведения кожи На каждую точку геометрии кожи влияют от одной до четырех костей, чтобы измерить их влияние, для каждой кости задаются некоторые веса. Тогда, если Wi — вес кости, причем Bi — матрица кости положение точки с учетом влияния костей расчитывается по формуле: V = V 0 * Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 21 Физическое моделирование – Моделирование поведения тряпок и твердых тел (на основе релаксированной сетке частиц) – Движение машины (с передним и задним приводом колес) Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 22 Физическое моделирование на основе частиц Уравнения движения частиц: каждая частица содержит два параметра такие, как: позиция x и мгновенная скорость v, которые вычисляют: x’ = x + v dt v’ = v + a dt или x’ = 2 x – x* + a dt 2 x* = x, где ее текущее положение x и предыдущее x* по II закону Ньютона: a = f / m; f – сила, действующая на частицу Релаксация системы: Моделирование тряпок Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 23 Движение машины Переднеприводная - - вслед за колесами поворачивается точка середины передней оси. смещается на расстояние, на которое сместилась машина. высчитывается угол между главной осью машины и отрезком с концами в центре машины и новым положением точки передней оси (это и есть угол поворота корпуса). Машина поворачивается и ее положение дотягивается до сдвинутой точки передней оси. Заднеприводная В случае заднеприводной происходят те же действия, только изначально поворачивается и сдвигается точка середины задней оси, и дотягивание производится относительно задней точки. Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum

Tough Modeling System 24 Физико-математический лицей № 30 Computer Graphics Support Group of 30 Phys – Math Lyceum