Topics in the border of economics and computation

Topics in the border of economics and computation seminar Gabrielle Demange, David gale, Matilda Sotomayor Presented by: Avinatan Hasidim Yair Weinberger

Menu 1. Definitions 2. Progressive auction mechanism – intuitive display 3. Proof of the progressive auction mechanism 4. Approximate auction mechanism – intuitive display 5. Proof of the approximate auction mechanism

Definitions • Let I denote a group of items and B a group of bidders. We assume a bidder can buy at most one item. • Each bidder assigns a value vb to every item in I, where vb N. • We will define a price p : I N. • The surplus of b given the item and a price vector p is vb - p( )

More Definitions 1. An assignment is a injective function : B’ I. Such that B’ B. 2. If (b) = we will say that assigns to b. 3. We will assume that there is a minimal price function s: I R, s. t. the owner of will not sell it at a price less than s( )

More Definitions • We will give an informal definition of an equilibrium – it is a state in which items are assigned to bidders s. t. everyone is “content”, in the meaning that 1. No bidder will be willing to offer more for an item in order to get it. 2. No seller is willing to reduce the price of an item in order to sell it.

We assume that the participants are kind hearted and honest.

The progressive auction mechanism • We will assume all valuations are integers. • We begin with the auctioneer reading an initial price vector P 0 which is equal to s. • At each stage each bidder says what items interest him – his demands set. • We will say that a set of items is over demanded if the number of bidders demanding only items from this set is greater then the number of items in this set.

The progressive auction mechanism – cont. • If we can assign to each bidder an item in his demand set then we are done. • Else there is an over demanded set. • With the help of hall’s assignment theorem the auctioneer finds the minimal over demanded set. • The auctioneer then raises the price of all the items in this set in one unit.

The progressive auction mechanism – cont. • The bidders then gives their new demands sets and the auctioneer repeats the above steps. • Obviously, the process will end, because in each step we raise the price of at least one item. Eventually, the price of the item will be greater then any of the bidders evaluations’.

Definitions • Db(p) = { : vb - p( )= max [vb - p( )]} I • A price is called competitive if there exists an assignment such that (b) Dp(b) • A couple (p, ) is called an equilibrium if p is competitive, is the assignment, and also if (b) then p( ) = s( ).

Convergence of the progressive auction mechanism Theorem (1) Let P be the price vector obtained from the progressive auction mechanism and let Q be any other competitive price then

Proof of theorem 1 By contradiction, At stage t=0, P Q, let t be the last stage that Pt Q. Now let’s look at stage t+1 We will prove that S-S 1 is not empty and overdemanded S: The minimal overdemanded set S 1: { | Pt+1( )>Q( )}

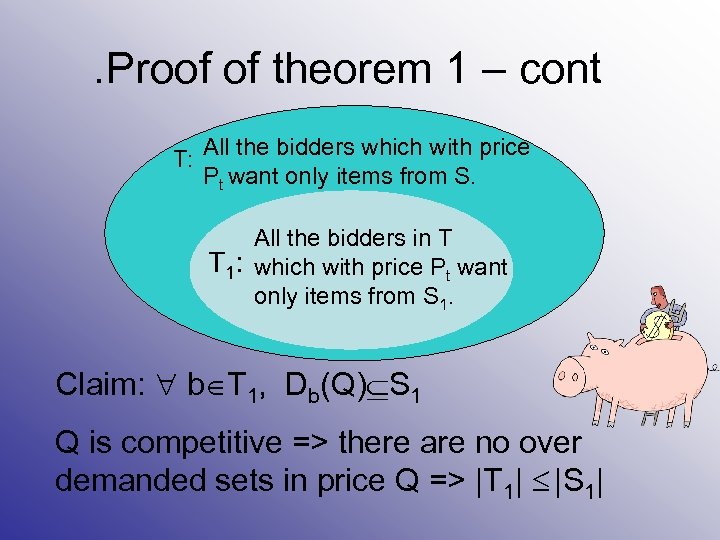
. Proof of theorem 1 – cont T: All the bidders which with price Pt want only items from S. All the bidders in T T 1: which with price Pt want only items from S 1. Claim: b T 1, Db(Q) S 1 Q is competitive => there are no over demanded sets in price Q => |T 1| |S 1|

. Proof of theorem 1 – cont T-T 1 is exactly the set of bidders which in price Pt want only items from S-S 1 From our previous claims it follows that |T-T 1|>|S-S 1| Thus S-S 1 is over demanded Contradiction (To the fact that S is minimal) Q. E. D.

Theorem (2): If p Is The Minimum Competitive Price Then There is an assignment * such that (p, *) is an equilibrium

• Let be an assignment and 1 an overpriced item in : P( 1)>S( 1) We will change to a different assignment in which will no longer be overpriced.

Theorem 2 – Building the Graph • • Vertices B I Edges - (b) = green Db(p) red B’ I’ – all the vertices reachable from 1

Case I • B’ contains an unassigned bidder • Let ( 1 b 1, 2 b 2… kbk , b) a path from 1 to b • Change the colors of arrows, like Hall’s theorem – define (b 1)= 1, (b 2)= 2 , …, (b)= k

Case II • Suppose all b B’ are assigned. • Claim – There exists ’ I’ such that p( ’ ) = s( ’ ). • Proof – If ’ does not exist we can lower all prices of items in I’. Since no b outside of B’ wants items from I’ we will have a lower competitive price – in contradiction to the minimality of p.

Case II - Continued • Choose ’ I’ s. t. p( ’) = s( ’) • Let ( 1 b 1, 2 b 2, …, kbk, ’) be a path from 1 to ’. • Again change the directions of the arrows and define (b 1)= 1, (b 2)= 2 , …, (bk)= k • ’ is unassigned but not overpriced Q. E. D.

The approximate auction mechanism • We begin with the auctioneer reading an initial price vector P 0 which is equal to s. • Any bidder may now bid for any item, we say that he is committed to that item.

The approximate auction mechanism – cont. • At a general stage, some bidders will be assigned to some items. Each uncommitted bidder may then: • 1. Bid for an unassigned item, he now becomes committed to that item. 2. Bid for an assigned item, he is now committed to this item, the price of this item raises by and all the bidders that were committed to this item are no uncommitted. 3. Drop out from the bidding.

Theorem (3): No Bidder Bids for an Item if at Time t its price pt( ) ≥ p( ) + k • Define is expansive at time t if pt( ) > p( ) • Lemma 1 – If b bids for an expansive item then he is assigned by . • Proof – if b were unassigned then for every item and especially for we have vb - p( ) 0, but then also vb - pt( ) 0 and then b wouldn’t bid for .

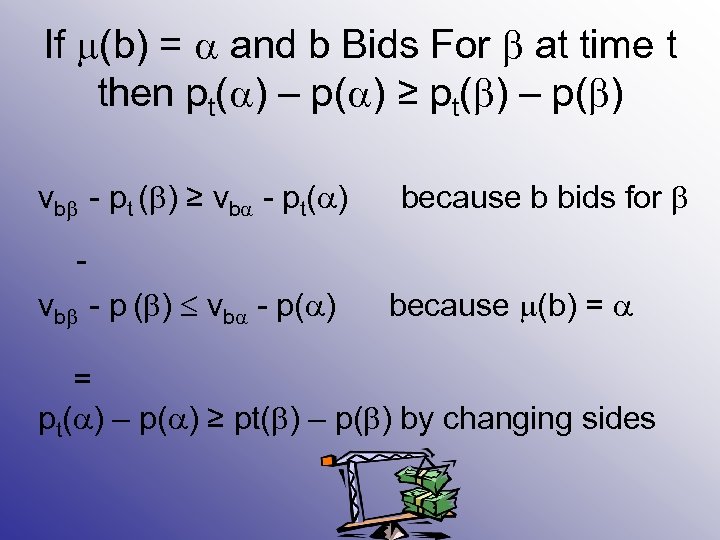
If (b) = and b Bids For at time t then pt( ) – p( ) ≥ pt( ) – p( ) vb - pt ( ) ≥ vb - pt( ) because b bids for vb - p ( ) vb - p( ) because (b) = = pt( ) – p( ) ≥ pt( ) – p( ) by changing sides

Back to Theorem 3 • Assume by contradiction that b 1 bids for when pt( ) ≥ p( ) + k and we will derive that k is unbounded, which is a contradiction. • is expensive b 1 is assigned to 1. (1) • pt( 1) – p( 1) ≥ pt( ) – pt( ) ≥ k (2) • pt( 1) ≥ p( 1) + k > p( 1) ≥ s( 1) • Thus some bidder b 2 is committed to 1 at time t…

Theorem 3 - continued • By lemma 1 b 2 is assigned by (b 2) = 2 • Since b 1 and b 2 are both assigned k ≥ 2. • 2 is expensive we need b 3, b 4… Q. E. D.

Theorem (4): pf( ) ≥ p( ) - k • The price obtained this way will not be too low. • We will assume that exists 1 s. t. pf( 1) < p( 1)- k • We will change sides and obtain (notice that the prices rise at ) p( 1) ≥ pf( ) + (k+1) > s( 1) • 1 is assigned by , say to b 1

. Theorem 4 cont • But then exists b’ 1 that demands 1 at price p, for else, one could decrease the price p and still have equilibrium. But b’ 1 is assigned to 2, that satisfies pf( 2) p( 2) - k. • Now we can deduce the existence of 3, 4, …, K+1 and this contradicts the definition of k. Q. E. D.

A more general model • Our model is good when we assign items to bidders. • Alas, sometimes the “items” have different prices for different bidders. For example, when we try to assign jobs to workers the workers may demand a different salary for each job. • How will that affect our auction mechanisms?

. A more general model - cont • Instead of a price vector we will use a price matrix, Swj of current salaries, where swj is the salary that w would demand if he were to accept job j. • An employer j would then choose those workers which vwj - swj is maximal.

Summary • We have seen two methods to perform an auction. • The first, the progressive auction mechanism, is an exact method but not comfortable to the bidders. • The second, the approximate auction mechanism is more comfortable and as accurate as one may wish.