Topics in Space Weather Lecture 11 The Upper

Topics in Space Weather Lecture 11 The Upper Atmosphere Robert R. Meier School of Computational Sciences George Mason University rmeier@gmu. edu CSI 769 15 November 2005 1

Remaining Lectures • Lecture 11 – November 15 – Upper Atmosphere • Lecture 12 – November 22 – Ionosphere – Geomagnetic storms • Lecture 13 – November 29 – Geomagnetic storms & magnetosphere connection – Aurora and Airglow • Lecture 14 – December 6 – Effects on Technological Systems – John Goodman will give last lecture 2

Topics - Lecture 11 • • • Sun as a star Solar effects on the atmosphere Upper atmospheric processes Temperature Density and composition Winds 3

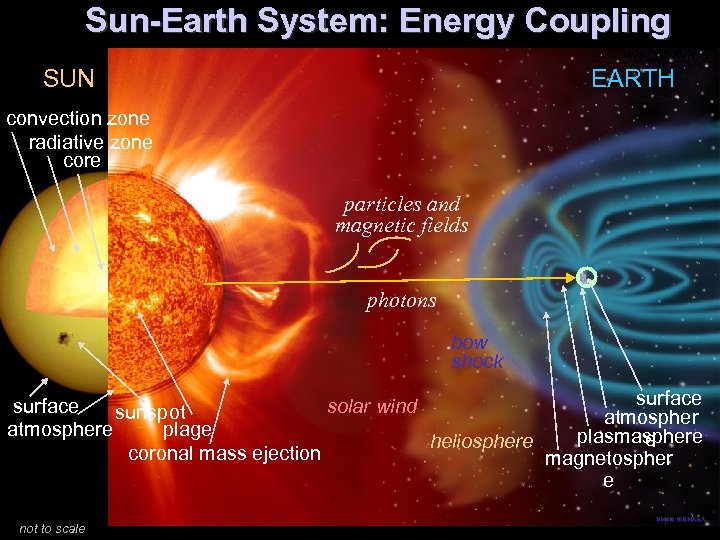Sun-Earth System: Energy Coupling SUN EARTH convection zone radiative zone core particles and magnetic fields photons bow shock surface solar wind sunspot atmosphere plage plasmasphere e heliosphere coronal mass ejection magnetospher e not to scale 4

SOLAR - TERRESTRIAL ENERGY SOURCES Source Deposition Solar Radiation Altitude • total Energy (Wm -2) 1366 Solar Cycle Change (Wm-2) 1. 2 surface • UV 200 -300 nm 15. 4 0. 17 • VUV 0 -200 0. 15 Particles nm • electron aurora III 0. 06 120 km • solar protons 0. 002 90 km Peak Joule Heating • galactic cosmic rays (strong storm) 0. 0000007 -1 • E=180 0. 4 90 km m. Vm 200 km Solar Wind 0. 0006 10 -80 km 50 -500 km 9030090 above 500 5

Sun as a Star 6

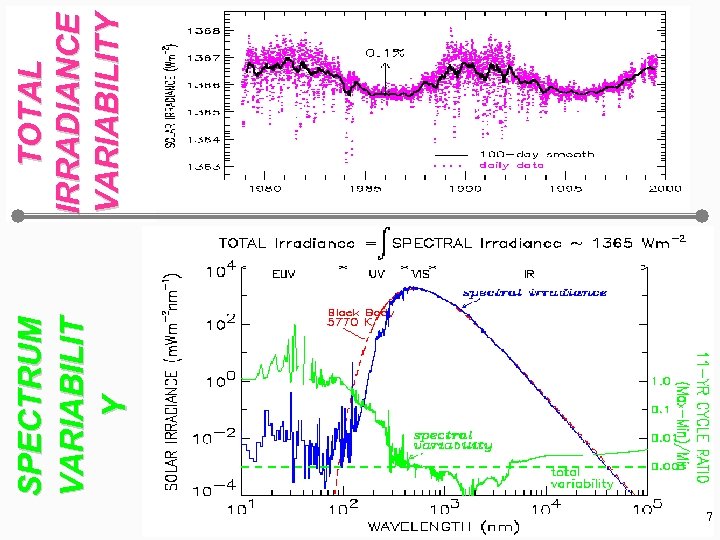7 SPECTRUM VARIABILIT Y TOTAL IRRADIANCE VARIABILITY

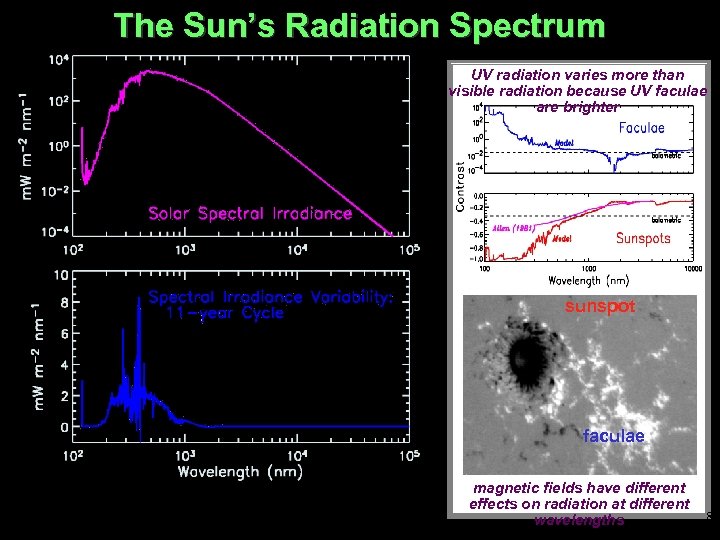The Sun’s Radiation Spectrum UV radiation varies more than visible radiation because UV faculae are brighter sunspot faculae magnetic fields have different effects on radiation at different wavelengths 8

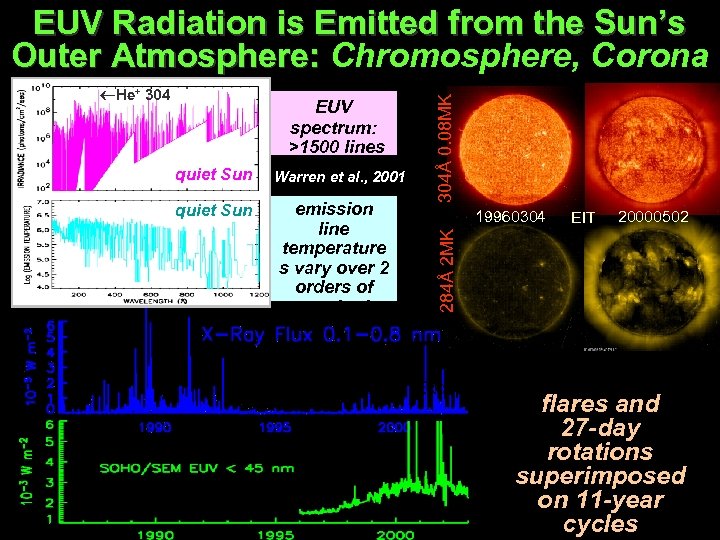quiet Sun EUV spectrum: >1500 lines 5 continua Warren et al. , 2001 emission line temperature s vary over 2 orders of magnitude 19960304 EIT 20000502 284Å 2 MK He+ 304Å 0. 08 MK EUV Radiation is Emitted from the Sun’s Outer Atmosphere: Chromosphere, Corona GOES 750 K Exospheric Temperature 1300 K flares and 27 -day rotations superimposed on 11 -year cycles 9

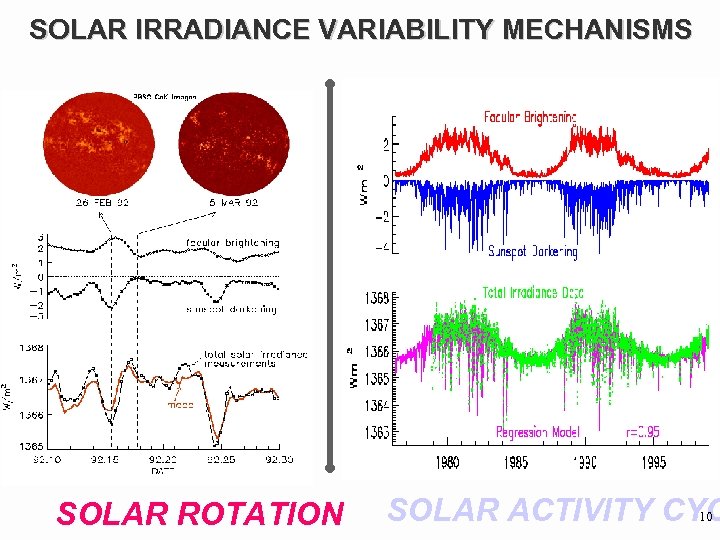SOLAR IRRADIANCE VARIABILITY MECHANISMS SOLAR ROTATION SOLAR ACTIVITY CYC 10

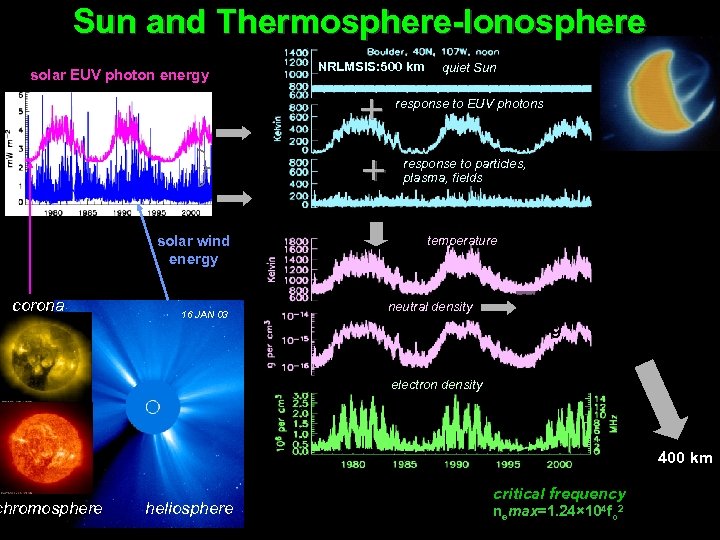Sun and Thermosphere-Ionosphere NRLMSIS: 500 km solar EUV photon energy Ap solar wind kinetic energy solar wind energy corona chromosphere 16 JAN 03 quiet Sun response to EUV photons response to particles, plasma, fields temperature neutral density NAVSPACECOM spacecraft drag electron density 400 km heliosphere critical frequency nemax=1. 24× 104 fo 2 11

304 quiet Sun EUV spectrum: >1500 lines 5 continua 304Å 0. 08 MK EUV Radiation is Emitted from the Sun’s Outer Atmosphere: Chromosphere, Corona quiet Sun Primary EUV Sources of Upper Atmosphere Heating: ch chromospheric cr coronal ch+cr mixed Roble, 1987 emission line temperature s vary over 2 orders of magnitude 750 K EIT 20000502 284Å 2 MK 19960304 Exospheric Temperature 1300 K 12

He II “ 304” Å Irradiance Variability 11 -year cycle SOHO/ 27 -day rotation model TIMED/ Solar Cycle EUV Spectrum Variability NRLEUV HFG EUVAC SOLAR 200 0 episodic flaring SEM “ 304”Å 5 min particle irradiance contaminati on 13

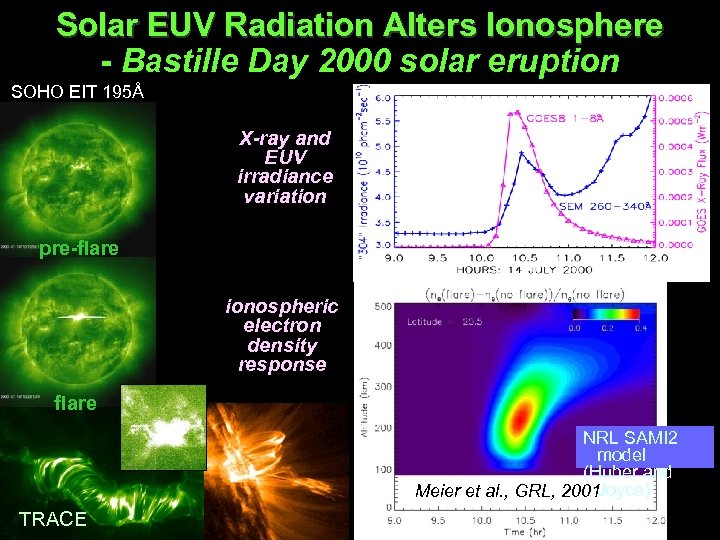Solar EUV Radiation Alters Ionosphere - Bastille Day 2000 solar eruption SOHO EIT 195Å X-ray and EUV irradiance variation pre-flare ionospheric electron density response flare NRL SAMI 2 model (Huber and Joyce) Meier et al. , GRL, 2001 TRACE 14

Availability of Solar XR, EUV & UV Data • Solar Extreme Ultraviolet (SEE) data from NASA/TIMED satellite – http: //lasp. colorado. edu/see/ • Solar Radiation and Climate Experiment (SORCE) – http: //lasp. colorado. edu/sorce/ • Solar EUV model (EUV 81) [Hinteregger et al. , Geophys. Res. Lett. 8, 1147 -1150, 1981] – Can be found at SEE website, along with other models (click on Data-General information and other data-Solar Irradiance Models) 15

Solar Effects on the Atmosphere 16

Solar Energy Deposition Atmospheric Structure SPACE WEATHER EUV FUV MUV RADIATION GLOBAL CHANGE 17

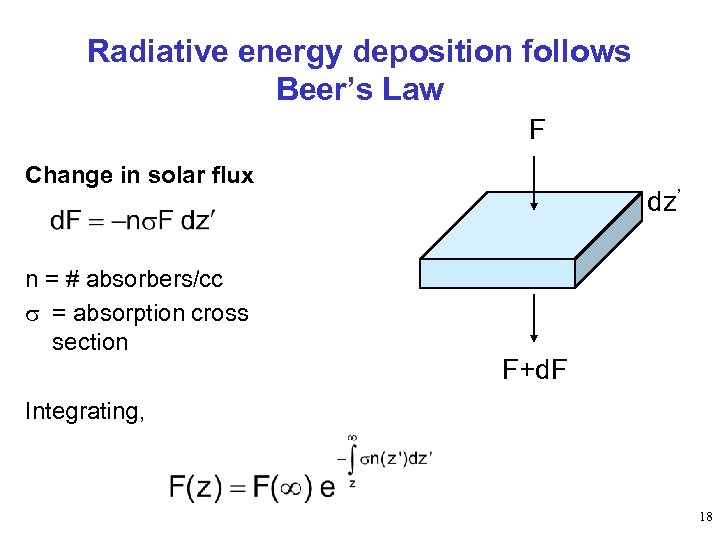Radiative energy deposition follows Beer’s Law F Change in solar flux n = # absorbers/cc s = absorption cross section dz’ F+d. F Integrating, 18

Optical Depth • Definition • For several species – i = N 2, O • Altitude of unit optical depth: F(z)= F( ) e-1 – Solve (z) = 1 for z (See slide 16) 19

Column Density • If const. , • Vertical Column Density number of atoms/molecules in a 1 cm 2 column above altitude z 20

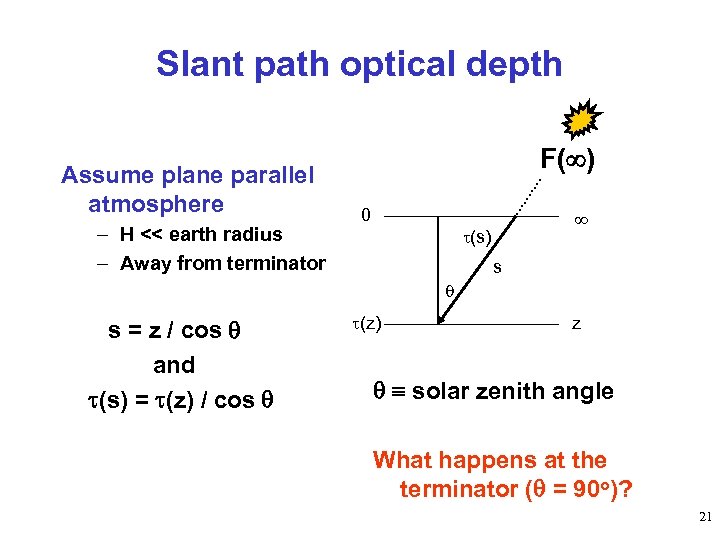Slant path optical depth Assume plane parallel atmosphere – H << earth radius – Away from terminator F( ) 0 (s) s s = z / cos and (s) = (z) / cos (z) z solar zenith angle What happens at the terminator ( = 90 o)? 21

Large solar zenith angles • Allowing for earth curvature and isothermal atmosphere, then: (s) = (z) Ch(x, ) – – X = (Re + z)/H Re = earth radius H = scale height Ch(x, ) = Chapman function * where + > 90 o and - < 90 o • Must do numerical integration along slant path from Sun: – If not isothermal – If accounting for oblate spheroid shape of Earth 22 * From Rishbeth and Garriott, Intro. To Iono. Phys.

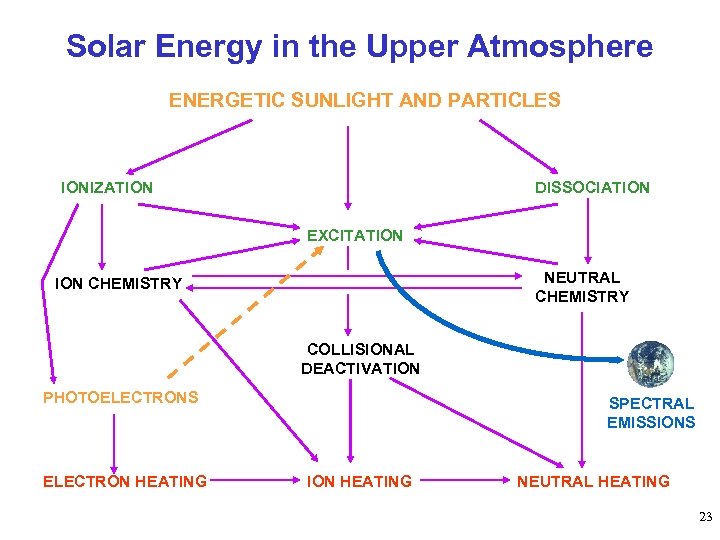Solar Energy in the Upper Atmosphere ENERGETIC SUNLIGHT AND PARTICLES IONIZATION DISSOCIATION EXCITATION NEUTRAL CHEMISTRY ION CHEMISTRY COLLISIONAL DEACTIVATION PHOTOELECTRONS ELECTRON HEATING SPECTRAL EMISSIONS ION HEATING NEUTRAL HEATING 23

Atmospheric Absorption Processes • Ionization – O 2 + h O 2+ + e*, … • Dissociation – N 2 + h N + N, … • Excitation – O + h O* • O* O + h ’ • O* + X O + X radiation quenching or deactivation • Dissociative ionization – excitation – N 2 + h N+* + N + e, …. . . 24

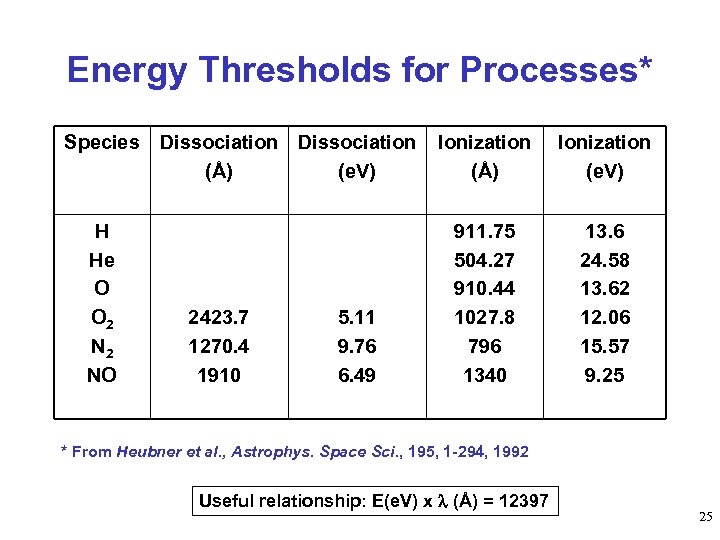Energy Thresholds for Processes* Species Dissociation (Å) (e. V) H He O O 2 NO 2423. 7 1270. 4 1910 5. 11 9. 76 6. 49 Ionization (Å) Ionization (e. V) 911. 75 504. 27 910. 44 1027. 8 796 1340 13. 6 24. 58 13. 62 12. 06 15. 57 9. 25 * From Heubner et al. , Astrophys. Space Sci. , 195, 1 -294, 1992 Useful relationship: E(e. V) x (Å) = 12397 25

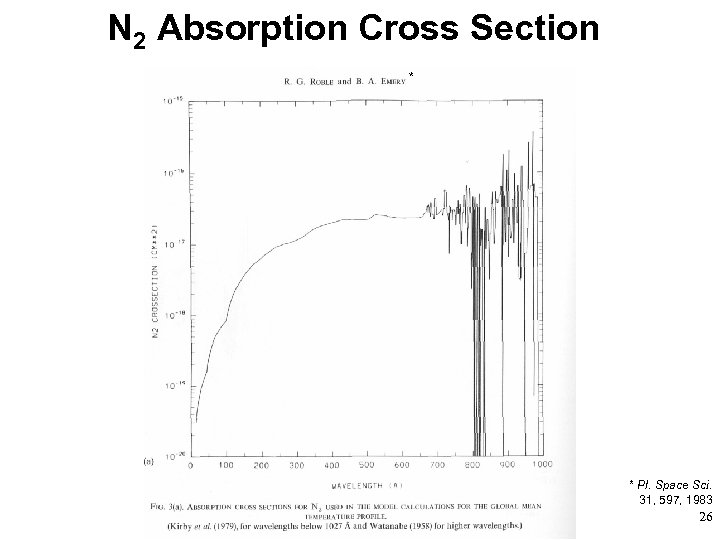N 2 Absorption Cross Section * * Pl. Space Sci. 31, 597, 1983 26

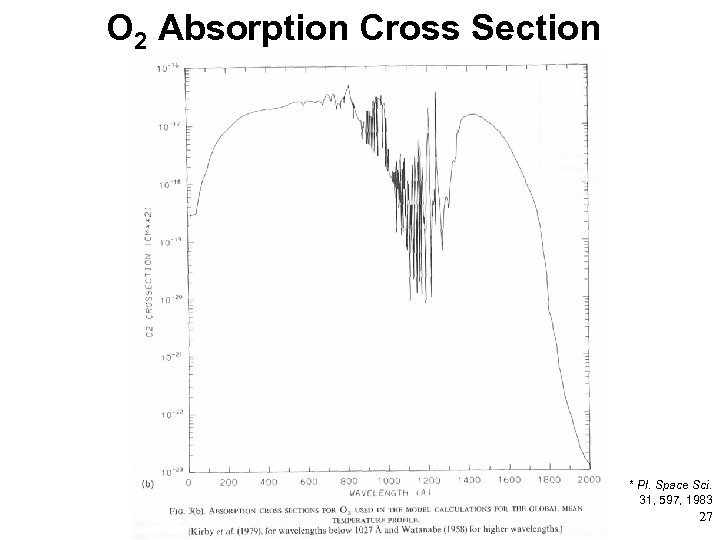O 2 Absorption Cross Section * * Pl. Space Sci. 31, 597, 1983 27

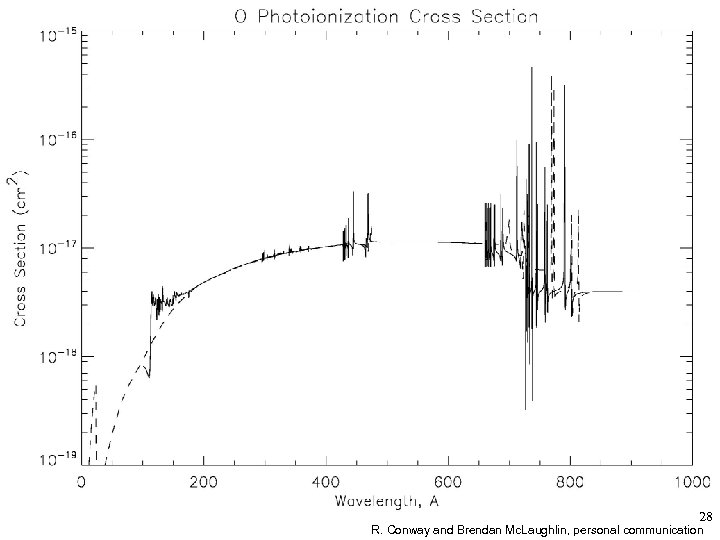28 R. Conway and Brendan Mc. Laughlin, personal communication

SOLAR CYCLE CHANGES IN EUV RADIATION IMPACT UPPER ATMOSPHERE TEMPERATURE and DENSITY Solar Cycle Changes at 700 km: Neutral Temperature: 2 times Neutral Density: 50 times Electron Density: 10 times 29

Atmospheric Processes Described by Thermospheric Global Circulation Models (GCMs) 30

GCM Physics: Upper Atmosphere Geoff Crowley Atmospheric & Space Technology Research Associates (ASTRA) 11118 Quail Pass San Antonio, TX 78249 210 -691 -0432 Objective: What’s required to build a GCM? (Equations, numerical techniques, parameterizations, boundary conditions, input specifications, validation with data) 31

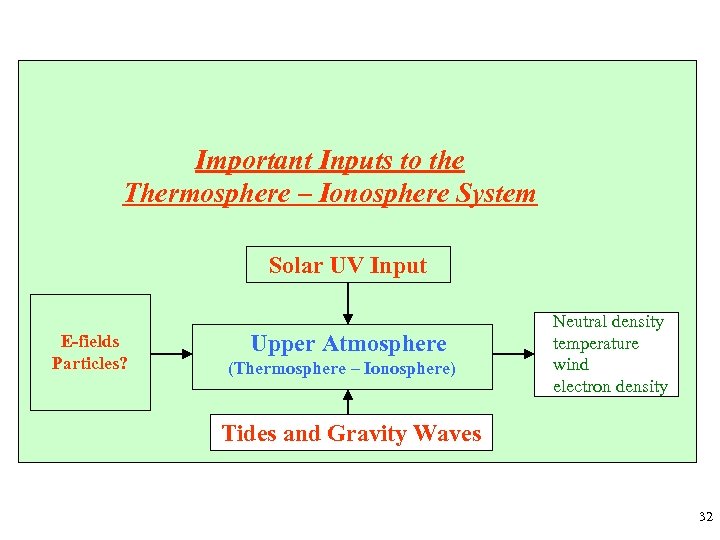Important Inputs to the Thermosphere – Ionosphere System Solar UV Input E-fields Particles? Upper Atmosphere (Thermosphere – Ionosphere) Neutral density temperature wind electron density Tides and Gravity Waves 32

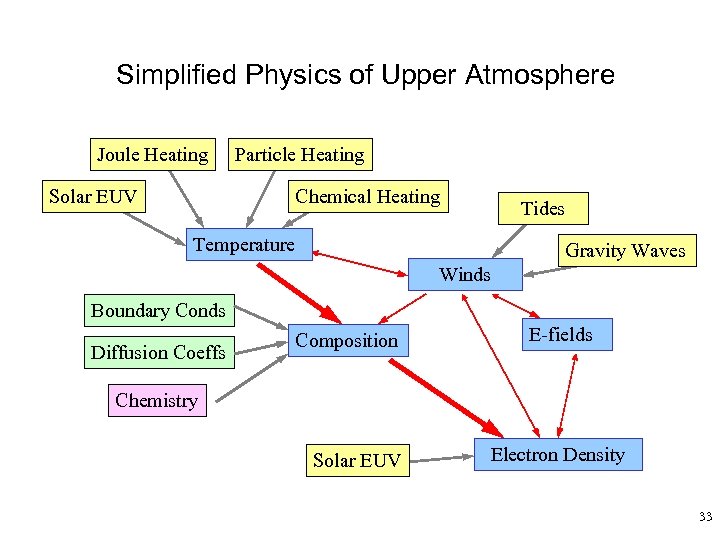Simplified Physics of Upper Atmosphere Joule Heating Solar EUV Particle Heating Chemical Heating Tides Temperature Gravity Waves Winds Boundary Conds Diffusion Coeffs Composition E-fields Chemistry Solar EUV Electron Density 33

Energy equation Molecular conduction radiation advection Many terms adiab. heating The leap-frog method is employed with vertical thermal conductivity treated implicitly to second order accuracy. This leads to a tridiagonal scheme requiring boundary conditions at the top and bottom of the domain as implied by the differential equation. Advection is treated implicitly to fourth order in the horizontal, second order in the vertical 34

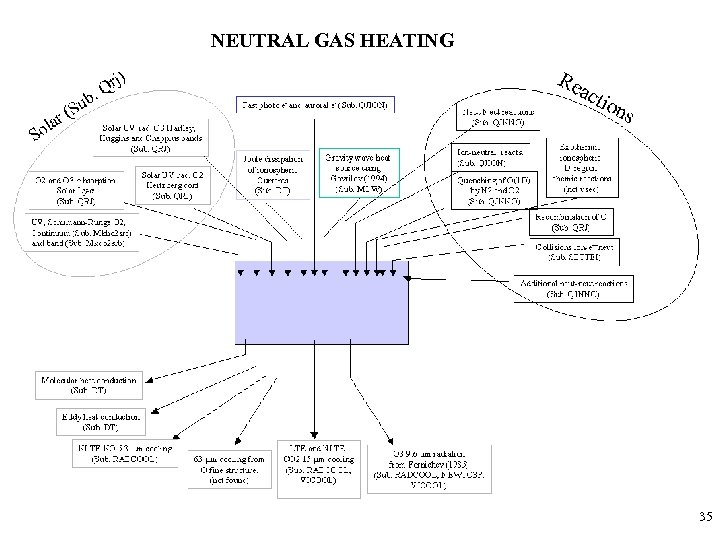NEUTRAL GAS HEATING 35

Continuity equation Vert. adv. molecular diffusion eddy diffusion Horiz. advection Recombination Production i is the mass mixing ratio for species i: i = I(z) / I(z), where is the mass density The leap-frog method is employed leading to a tridiagonal scheme requiring boundary conditions at the top and bottom of the domain. 36

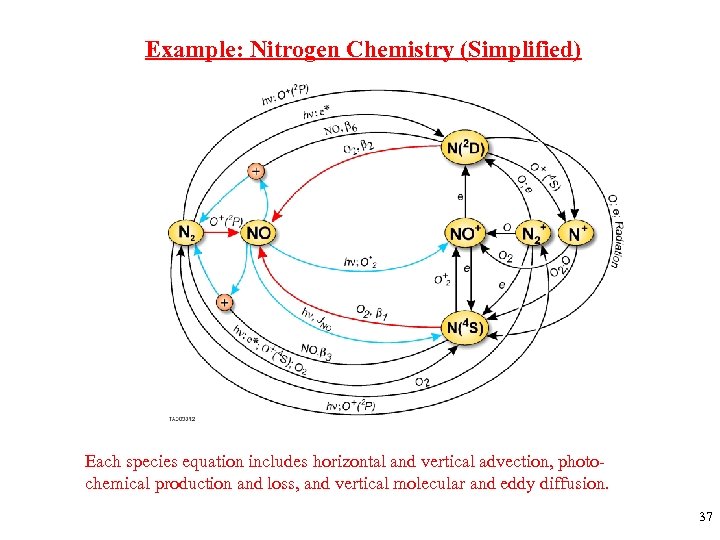Example: Nitrogen Chemistry (Simplified) Each species equation includes horizontal and vertical advection, photochemical production and loss, and vertical molecular and eddy diffusion. 37

Neutral Species The model includes 15 separate neutral species, not counting some excited states which are also tracked. CO 2, O, N 2, CO, O 2, O 3, H, H 2 O, HO 2, N, NO 2, Ar, and He. Ionized Species The model includes 7 ion species O+, N+, CO 2+, NO+, and H+ with ionization primarily from solar EUV and x-ray. The ions are assumed to be in photochemical equilibrium with one another and the free electrons. 38

Momentum equations Zonal velocity Coriolis Viscosity (Molecular and Eddy) ion drag Rayleigh friction momentum advection Pressure gradients gravity wave drag Meridional velocity The Leap frog method is employed with vertical molecular viscosity treated implicitly to second order accuracy. Since the zonal and meridional momentum equations are coupled through Coriolis and off-diagonal ion drag terms, the system reduces to a diagonal block matrix scheme, where (2 x 2) matrices and two component vectors are used at each level. Boundary conditions for the zonal (u) and meridional ( v) wind components are needed at the top and bottom of the model. 39

Upper atmospheric temperature, density and composition Some simplified concepts 40

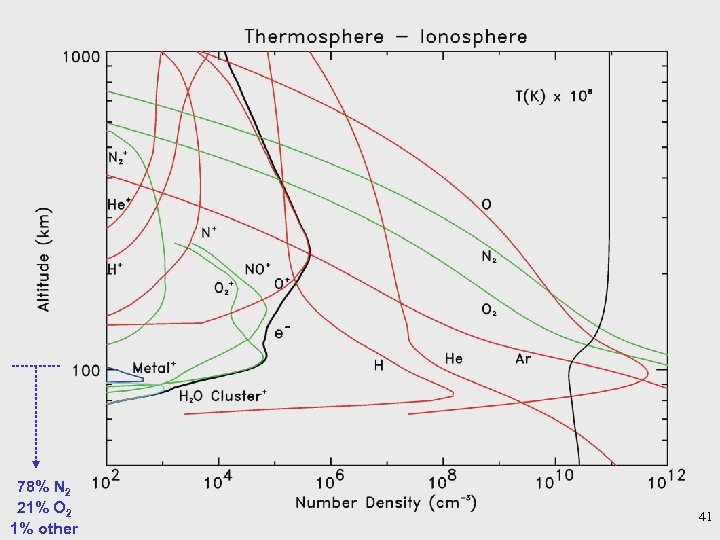78% N 2 21% O 2 1% other 41

Thermodynamics • Temperature equation very difficult to solve • Even under simplified 1 -D geometry, the temperature equation is a 2 nd order timedependent PDE – See Equation 8. 77 of Gombosi • Net heating rate (Production – Loss) is positive in thermosphere (low cooling rate) – Leads to increase in temperature with altitude – Heat conducted downward and radiated to space in the lower thermosphere by CO 2, NO, and small amount of O fine structure radiation 42

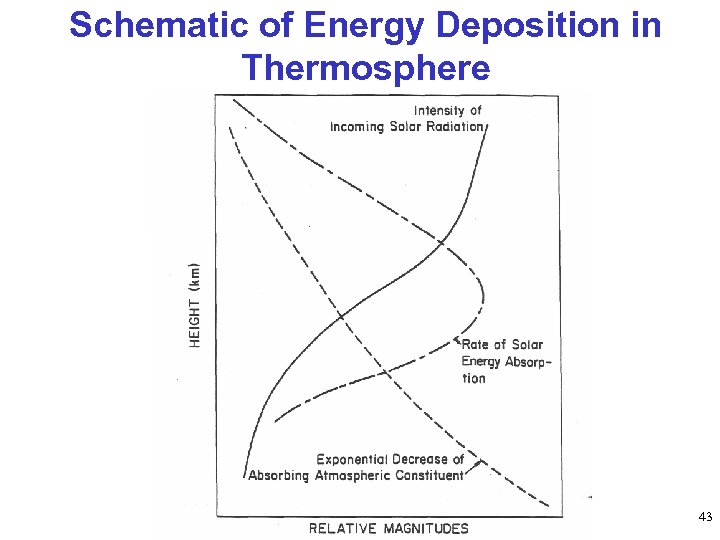Schematic of Energy Deposition in Thermosphere 43

Bates [1959] Temperature Profile Analytic approximation for temperature profile: T(z) = T - (T - Tzo) e-s(z – zo) – s = shape function » Varies with conditions » typical ~ 0. 02 km-1 – Matches observations – Functional form agrees with GCM models 44

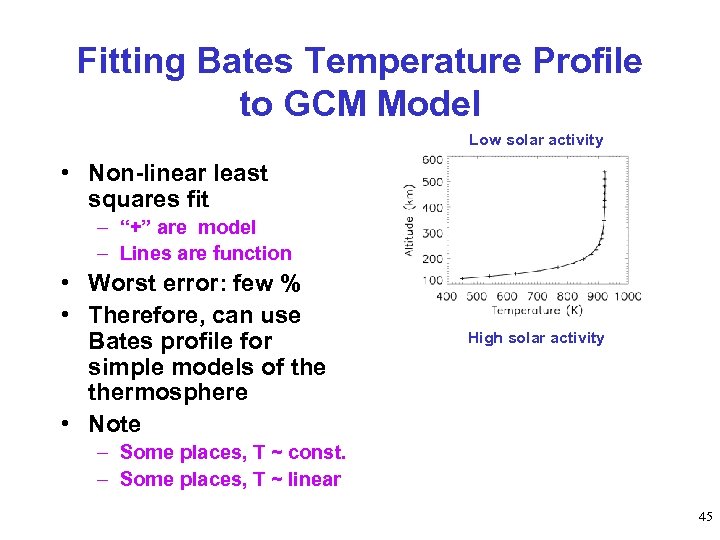Fitting Bates Temperature Profile to GCM Model Low solar activity • Non-linear least squares fit – “+” are model – Lines are function • Worst error: few % • Therefore, can use Bates profile for simple models of thermosphere • Note High solar activity – Some places, T ~ const. – Some places, T ~ linear 45

Diffusion • Eddy diffusion – Turbulent mixing/wave breaking approximated by diffusion of small eddys • Molecular diffusion – Each species follows its own scale height • Turbopause – Where eddy and molecular diffusion rates are equal – Typically ~ 105 km • But transition is smooth over some altitude interval • Below is called the homosphere • Above is the heterosphere 46

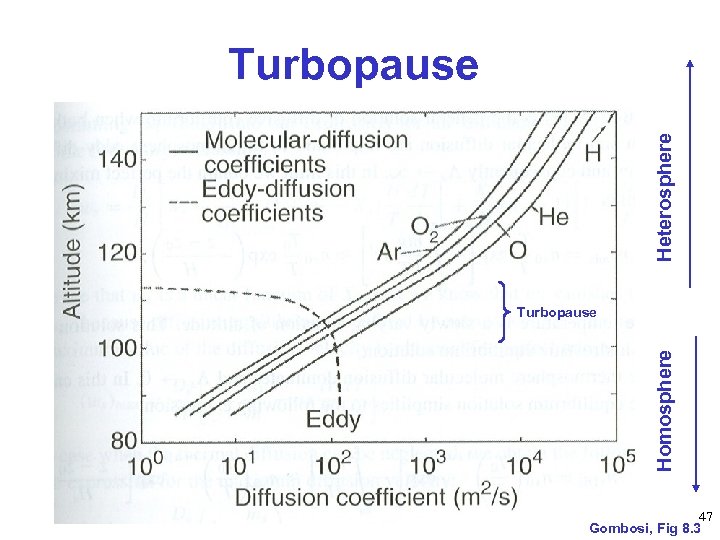Heterosphere Turbopause Homosphere Turbopause 47 Gombosi, Fig 8. 3

Diffusive Equilibrium • Maxwell-Boltzmann velocity distribution • No net vertical diffusion velocity • No chemistry • Steady-state, static equilibrium – Ignore velocities • Chapter 8 [Gombosi] 48

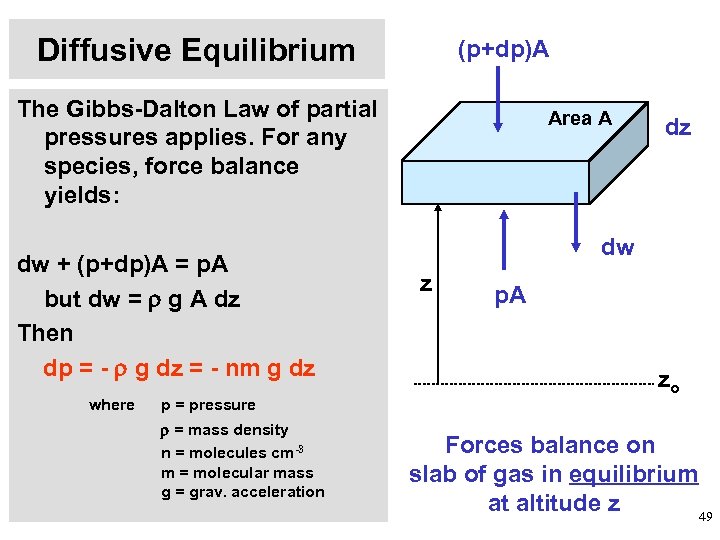Diffusive Equilibrium (p+dp)A The Gibbs-Dalton Law of partial pressures applies. For any species, force balance yields: dw + (p+dp)A = p. A but dw = g A dz Then dp = - g dz = - nm g dz where p = pressure = mass density n = molecules cm-3 m = molecular mass g = grav. acceleration Area A dz dw z p. A zo Forces balance on slab of gas in equilibrium at altitude z 49

Combine with Ideal Gas Law p=nk. T dp = k. T dn + nk d. T = - nm g dz dividing by nk. T dn/n + d. T/T + dz/H = 0 where H = k. T/(mg) If T and g constant, then n(z) = n(zo) e-(z-z )/H Note-Earth is an oblate spheroid: - Equatorial Radius: 6378 km & g = 9. 78 m/s 2 - Polar Radius: 6357 km & g = 9. 83 m/s 2 - Mean Radius: 6371 km o 50

Barometric Equation From Ideal Gas Law p=nk. T And with n(z) = n(zo) e-(z-z )/H o Substituting: p(z) = p(zo) e-(z-z )/H o This applies over small altitude intervals or at high altitudes where T is ~ constant 51

Non-isothermal Atmosphere Diffusive equilibrium: dn/n + d. T/T + dz/H = 0 d Log n + d Log T = - dz/H Integrating: n(z) = n(zo) T(zo)/T(z) e- dz/H or p(z) = p(zo) e- dz/H 52

Multi-constituent Atmosphere Total Pressure: p(z) = pi where i = N 2, O Test for Diffusive Equilibrium dpi = - ni mi g dz = - pi mi g dz / (k. T) Solving for g/(k. T) for species I and j, leads to: Integrating, I=atomic mass of i Meier et al. JGR, 106, 15519, 2001 53

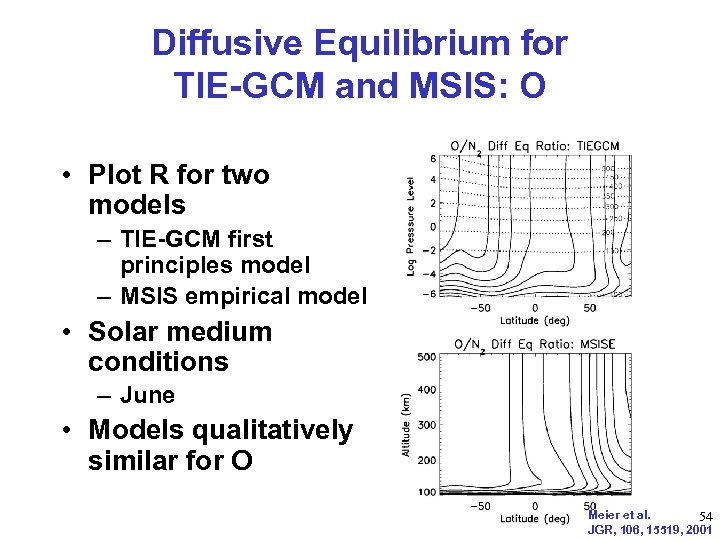Diffusive Equilibrium for TIE-GCM and MSIS: O • Plot R for two models – TIE-GCM first principles model – MSIS empirical model • Solar medium conditions – June • Models qualitatively similar for O Meier et al. 54 JGR, 106, 15519, 2001

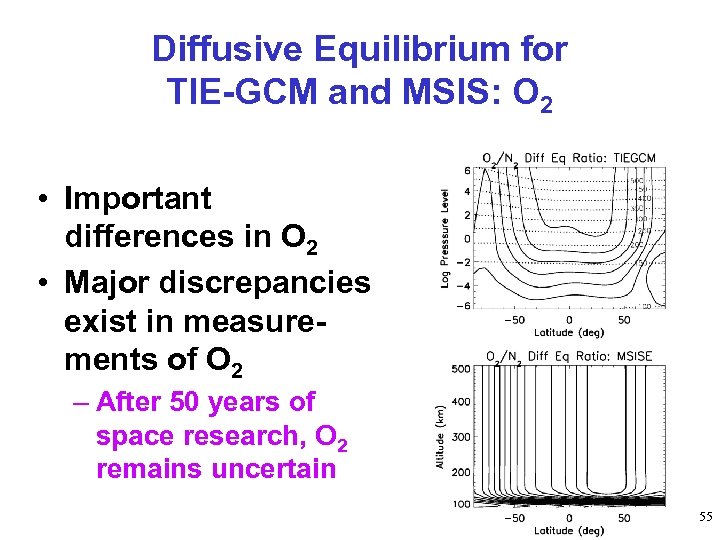Diffusive Equilibrium for TIE-GCM and MSIS: O 2 • Important differences in O 2 • Major discrepancies exist in measurements of O 2 – After 50 years of space research, O 2 remains uncertain 55

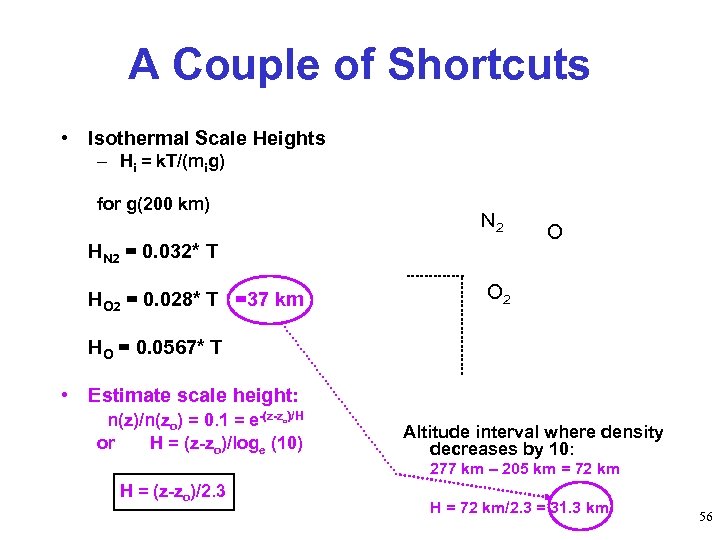A Couple of Shortcuts • Isothermal Scale Heights – Hi = k. T/(mig) for g(200 km) N 2 HN 2 = 0. 032* T HO 2 = 0. 028* T =37 km O O 2 HO = 0. 0567* T • Estimate scale height: n(z)/n(zo) = 0. 1 = e-(z-z )/H or H = (z-zo)/loge (10) o Altitude interval where density decreases by 10: 277 km – 205 km = 72 km H = (z-zo)/2. 3 H = 72 km/2. 3 = 31. 3 km 56

Bates-Walker Model Atmosphere [Walker, J. Atmos. Sci, 22, 462, 1965] Using the Bates T(z): T(z) = T – (T - Tzo) e-s(z-zo)) And diffusive equilibrium: ni(z) = ni(zo) T(zo)/T(z) e- dz/Hi And changing to geopotential altitude: = (z-zo)(Re+ zo)/(Re+ z) Then where 57

Bates-Walker Model Atmosphere cont. • Gives good representation of atmosphere in diffusive equilibrium • Basis of many atmospheric studies • Basis of MSIS-class empirical models of the upper atmosphere – Needs to be modified for O and O 2 photochemistry, which is important below ~ 200 km 58

Departures from Diffusive Equilibrium: Simplified O 2 Photochemistry* • Loss O 2 + h O + O • Production O + M O 2 + M • Diffusion time t. D = H 2/D j = 4. 2 to 6. 8 x 10 -6 s-1 solar min to max t. L = j-1 = 2. 4 to 1. 5 x 105 s k = 2. 76 x 10 -34 e 710/T cm 6 s-1 t. P = (k n. O n. M)-1 s t. D(110 km) ~ 2. 4 x 105 s t. D(120 km) ~ 1. 2. x 105 s • Therefore O 2 not in diffusive equilibrium (t. L ~ t. D) 59 * Other O 2 photochemistry also involved: Gombosi, 8. 8. 2

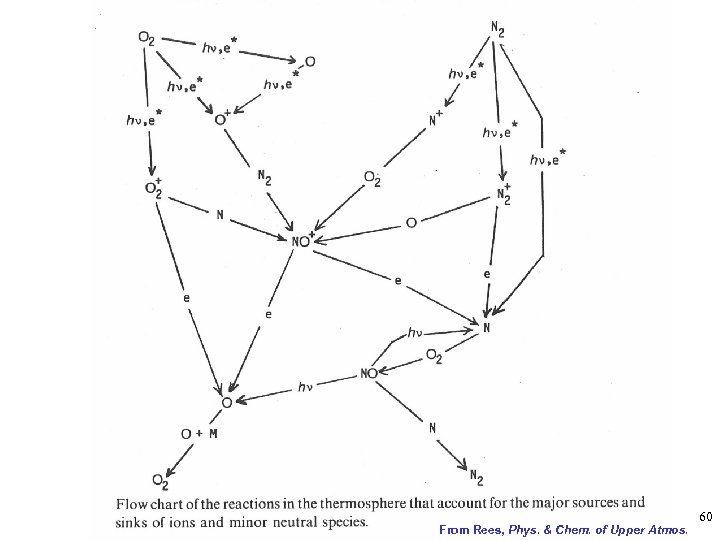From Rees, Phys. & Chem. of Upper Atmos. 60

MSIS Class Empirical Atmospheric Models • MSIS-class Models Are the Community Standard • Inputs: Day, Time (UT, Apparent Solar Local Time), Location, Solar EUV Flux Proxy (F 10. 7 , F 10. 7 81 day ave), Magnetic Activity (ap, Ap) • Outputs: Composition (N 2, O, N, He, Ar, H, Oa), Total Mass Density, and Temperature, 0 - 1000 km • Empirical, Analytic, Assimilative – Spherical Harmonics + Bates-Walker Altitude Profile – Interpolates Among Or Extrapolates Numerous Data Sets To User-Specified Inputs – Nominal 1 s Error 15 -25 % (vs Altitude/Latitude) • NRLMSIS 2000 E supercedes MSISE-90: Automated/Web Distribution 61

MSIS Data Bases • Data Sets Incorporated Into NRLMSIS – Satellites (Mass spectrometer [MS], EUV absorption) – Rockets (MS, Pressure gauge, falling sphere, grenade) – Ground-based Incoherent Scatter Radar (ISR) – Middle Atmosphere Program (MAP) Handbook Tables – Satellite Drag, Accelerometer – Recent O 2 Data: Solar Maximum Mission (SMM) • Data Sets Yet To Be Incorporated – Upper Atmosphere Research Satellite (UARS) – NRL/DOD UV Remote Sensing: ARGOS, SSULI 62

MSIS Accessibility • Description and downloading: – http: //uap-www. nrl. navy. mil/models_web/msis_home. htm – http: //modelweb. gsfc. nasa. gov/models/msis. html • MSIS 90 (earlier version) • Reference to NRLMSIS 2000 – Picone, J. M. , A. E. Hedin, D. P. Drob, and A. C. Aikin, J. Geophys. Res. , 107(A 12), 1468 (2002) • MSIS solar-geophysical inputs can be found at: – ftp: //ftp. ngdc. noaa. gov/STP/GEOMAGNETIC_DATA/INDICES/KP_AP/ – http: //www. sec. noaa. gov/today. html 63

NRLMSIS Example: March 21 F 10. 7 = 150, Ap = 4 , Altitude = 300 km 64

NRLMSIS Example: June 21 F 10. 7 = 150, Ap = 4, Altitude = 300 km 65

How Good are the Models? • Compare MSIS & TIE-GCM Models Solar-Geophysical Conditions • • Summer Solstice Solar Medium Low Geomagnetic Latitudes Longitudes Altitude Range GMT June 19 F 10. 7=150 Ap = 4 -60 to + 60 o all 110 – 478 km 00: 00 H • Plot Ratios of GCM/MSIS Parameters 66

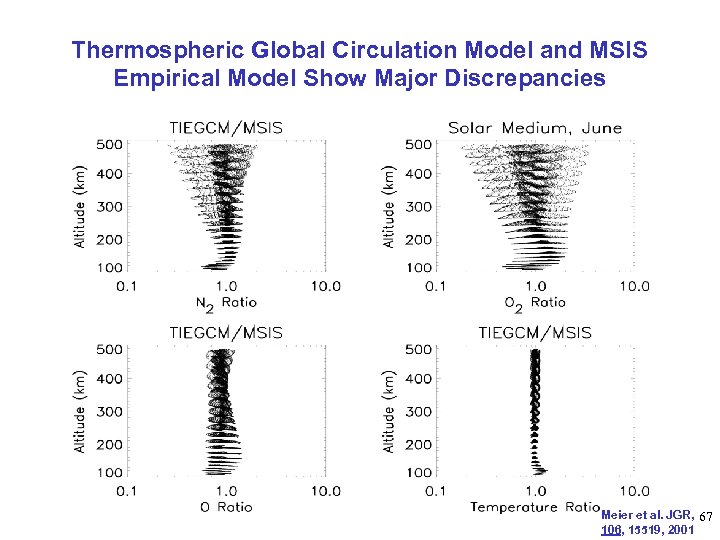Thermospheric Global Circulation Model and MSIS Empirical Model Show Major Discrepancies Meier et al. JGR, 67 106, 15519, 2001

Upper Atmospheric Dynamics Short Summary (More after ionosphere and geomagnetic storm lectures) 68

Atmospheric Momentum Sources • Solar (Heating) Tide • Coriolis Force • Ion Drag • Gravity Waves 69

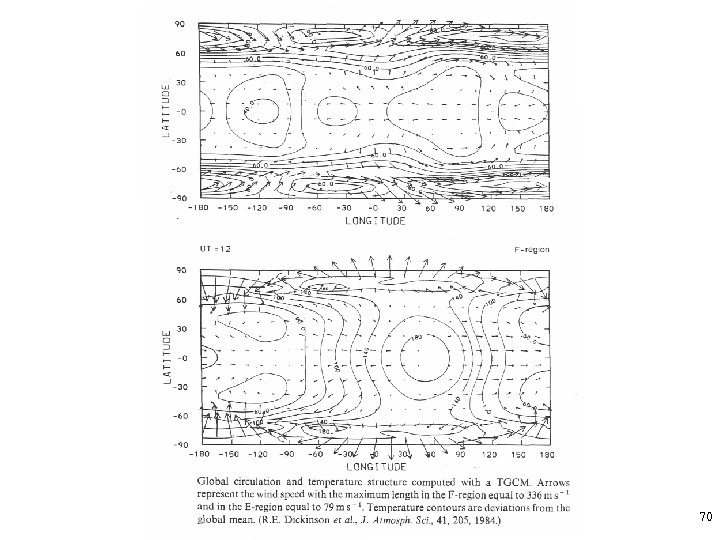70

Altitude-Latitude Variation of Thermospheric Circulation from GCM Model Geomagnetic Activity Quiet Average Storm 71