c5704c42dad97007f2818d6fa3812812.ppt
- Количество слайдов: 72
 Topic Uncertainty
Topic Uncertainty
 Uncertainty is Pervasive u What is uncertain in economic systems? – tomorrow’s prices – future wealth – future availability of commodities – present and future actions of other people.
Uncertainty is Pervasive u What is uncertain in economic systems? – tomorrow’s prices – future wealth – future availability of commodities – present and future actions of other people.
 Uncertainty is Pervasive u What are rational responses to uncertainty? – buying insurance (health, life, auto) – a portfolio of contingent consumption goods.
Uncertainty is Pervasive u What are rational responses to uncertainty? – buying insurance (health, life, auto) – a portfolio of contingent consumption goods.
 States of Nature u Possible states of Nature: – “car accident” (a) – “no car accident” (na). u Accident occurs with probability a, does not with probability na ; a + na = 1. u Accident causes a loss of Rs. L.
States of Nature u Possible states of Nature: – “car accident” (a) – “no car accident” (na). u Accident occurs with probability a, does not with probability na ; a + na = 1. u Accident causes a loss of Rs. L.
 Contingencies u. A contract implemented only when a particular state of Nature occurs is state-contingent. u E. g. the insurer pays only if there is an accident.
Contingencies u. A contract implemented only when a particular state of Nature occurs is state-contingent. u E. g. the insurer pays only if there is an accident.
 Contingencies u. A state-contingent consumption plan is implemented only when a particular state of Nature occurs. u E. g. take a vacation only if there is no accident.
Contingencies u. A state-contingent consumption plan is implemented only when a particular state of Nature occurs. u E. g. take a vacation only if there is no accident.
 State-Contingent Budget Constraints u Each Rs. 1 of accident insurance costs . u Consumer has Rs. m of wealth. u Cna is consumption value in the noaccident state. u Ca is consumption value in the accident state.
State-Contingent Budget Constraints u Each Rs. 1 of accident insurance costs . u Consumer has Rs. m of wealth. u Cna is consumption value in the noaccident state. u Ca is consumption value in the accident state.
 State-Contingent Budget Constraints Cna Ca
State-Contingent Budget Constraints Cna Ca
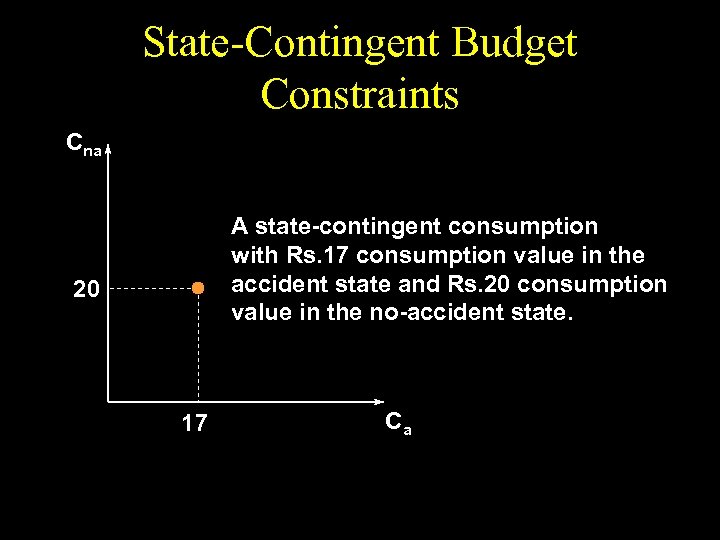 State-Contingent Budget Constraints Cna A state-contingent consumption with Rs. 17 consumption value in the accident state and Rs. 20 consumption value in the no-accident state. 20 17 Ca
State-Contingent Budget Constraints Cna A state-contingent consumption with Rs. 17 consumption value in the accident state and Rs. 20 consumption value in the no-accident state. 20 17 Ca
 State-Contingent Budget Constraints u Without insurance, u Ca = m - L u Cna = m.
State-Contingent Budget Constraints u Without insurance, u Ca = m - L u Cna = m.
 State-Contingent Budget Constraints Cna m The endowment bundle. Ca
State-Contingent Budget Constraints Cna m The endowment bundle. Ca
 State-Contingent Budget Constraints u Buy Rs. K of accident insurance. u Cna = m - K. u Ca = m - L - K + K = m - L + (1 - )K.
State-Contingent Budget Constraints u Buy Rs. K of accident insurance. u Cna = m - K. u Ca = m - L - K + K = m - L + (1 - )K.
 State-Contingent Budget Constraints u Buy Rs. K of accident insurance. u Cna = m - K. u Ca = m - L - K + K = m - L + (1 - )K. u So K = (Ca - m + L)/(1 - )
State-Contingent Budget Constraints u Buy Rs. K of accident insurance. u Cna = m - K. u Ca = m - L - K + K = m - L + (1 - )K. u So K = (Ca - m + L)/(1 - )
 State-Contingent Budget Constraints u Buy Rs. K of accident insurance. u Cna = m - K. u Ca = m - L - K + K = m - L + (1 - )K. u So K = (Ca - m + L)/(1 - ) u And Cna = m - (Ca - m + L)/(1 - )
State-Contingent Budget Constraints u Buy Rs. K of accident insurance. u Cna = m - K. u Ca = m - L - K + K = m - L + (1 - )K. u So K = (Ca - m + L)/(1 - ) u And Cna = m - (Ca - m + L)/(1 - )
 State-Contingent Budget Constraints u Buy Rs. K of accident insurance. u Cna = m - K. u Ca = m - L - K + K = m - L + (1 - )K. u So K = (Ca - m + L)/(1 - ) u And Cna = m - (Ca - m + L)/(1 - ) u I. e.
State-Contingent Budget Constraints u Buy Rs. K of accident insurance. u Cna = m - K. u Ca = m - L - K + K = m - L + (1 - )K. u So K = (Ca - m + L)/(1 - ) u And Cna = m - (Ca - m + L)/(1 - ) u I. e.
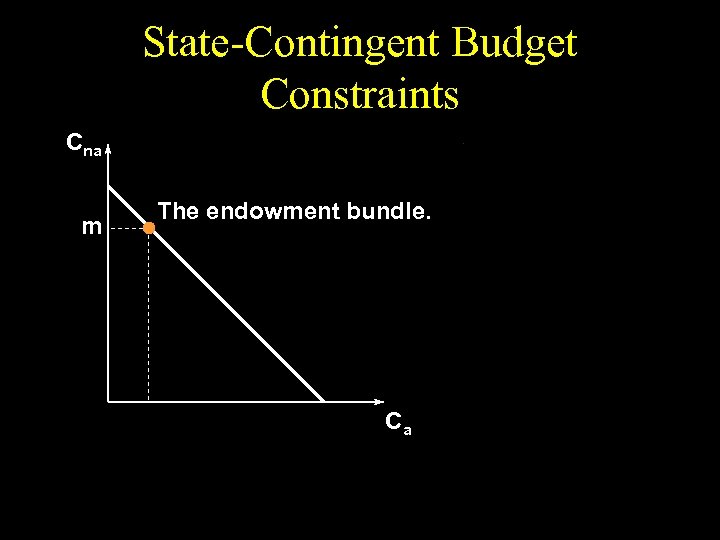 State-Contingent Budget Constraints Cna m The endowment bundle. Ca
State-Contingent Budget Constraints Cna m The endowment bundle. Ca
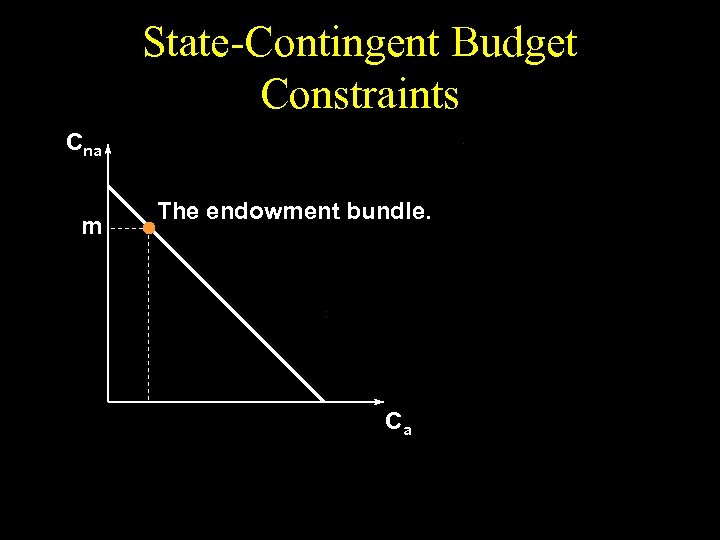 State-Contingent Budget Constraints Cna m The endowment bundle. Ca
State-Contingent Budget Constraints Cna m The endowment bundle. Ca
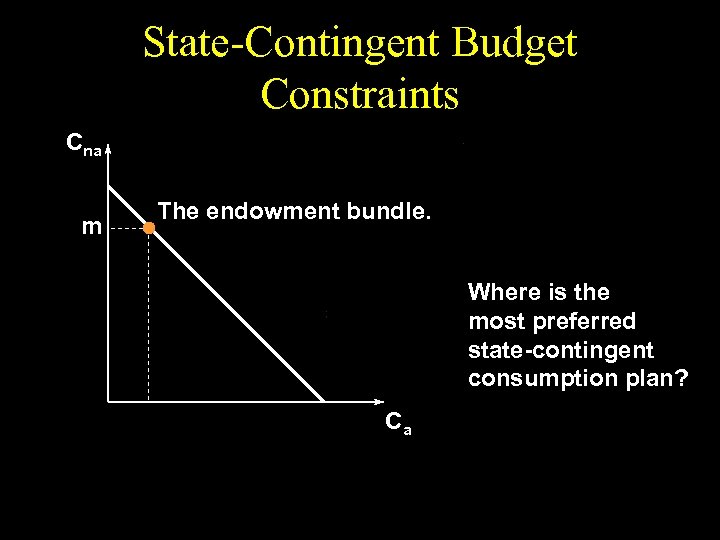 State-Contingent Budget Constraints Cna m The endowment bundle. Where is the most preferred state-contingent consumption plan? Ca
State-Contingent Budget Constraints Cna m The endowment bundle. Where is the most preferred state-contingent consumption plan? Ca
 Preferences Under Uncertainty u Think of a lottery. u Win Rs. 90 with probability 1/2 and win Rs. 0 with probability 1/2. u U(Rs. 90) = 12, U(Rs. 0) = 2. u Expected utility is
Preferences Under Uncertainty u Think of a lottery. u Win Rs. 90 with probability 1/2 and win Rs. 0 with probability 1/2. u U(Rs. 90) = 12, U(Rs. 0) = 2. u Expected utility is
 Preferences Under Uncertainty u Think of a lottery. u Win Rs. 90 with probability 1/2 and win Rs. 0 with probability 1/2. u U(Rs. 90) = 12, U(Rs. 0) = 2. u Expected utility is
Preferences Under Uncertainty u Think of a lottery. u Win Rs. 90 with probability 1/2 and win Rs. 0 with probability 1/2. u U(Rs. 90) = 12, U(Rs. 0) = 2. u Expected utility is
 Preferences Under Uncertainty u Think of a lottery. u Win Rs. 90 with probability 1/2 and win Rs. 0 with probability 1/2. u Expected money value of the lottery is
Preferences Under Uncertainty u Think of a lottery. u Win Rs. 90 with probability 1/2 and win Rs. 0 with probability 1/2. u Expected money value of the lottery is
 Preferences Under Uncertainty u EU = 7 and EM = Rs. 45. u U(Rs. 45) > 7 Rs. 45 for sure is preferred to the lottery risk-aversion. u U(Rs. 45) < 7 the lottery is preferred to Rs. 45 for sure risk-loving. u U(Rs. 45) = 7 the lottery is preferred equally to Rs. 45 for sure riskneutrality.
Preferences Under Uncertainty u EU = 7 and EM = Rs. 45. u U(Rs. 45) > 7 Rs. 45 for sure is preferred to the lottery risk-aversion. u U(Rs. 45) < 7 the lottery is preferred to Rs. 45 for sure risk-loving. u U(Rs. 45) = 7 the lottery is preferred equally to Rs. 45 for sure riskneutrality.
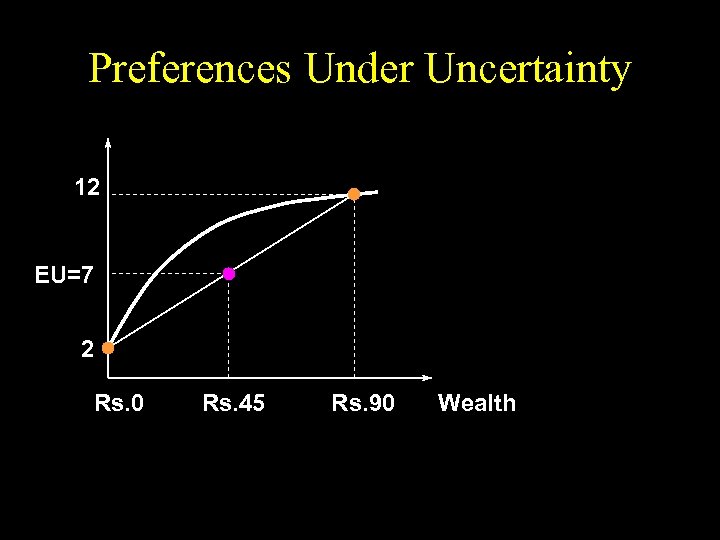 Preferences Under Uncertainty 12 EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
Preferences Under Uncertainty 12 EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
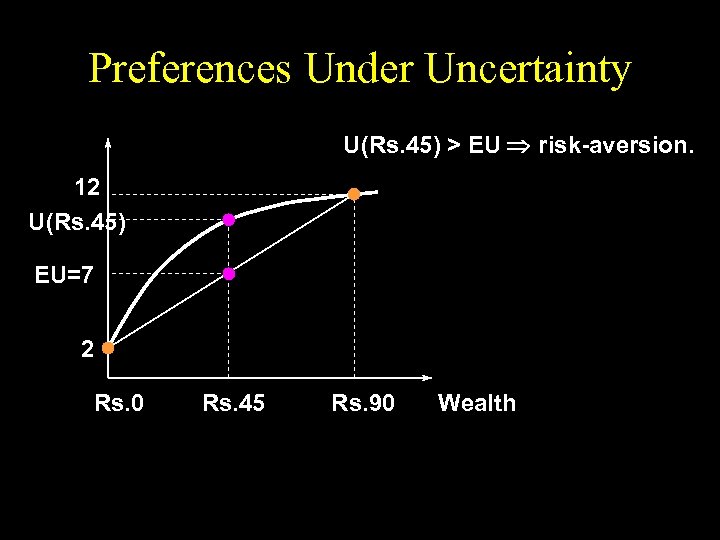 Preferences Under Uncertainty U(Rs. 45) > EU risk-aversion. 12 U(Rs. 45) EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
Preferences Under Uncertainty U(Rs. 45) > EU risk-aversion. 12 U(Rs. 45) EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
 Preferences Under Uncertainty U(Rs. 45) > EU risk-aversion. 12 U(Rs. 45) MU declines as wealth rises. EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
Preferences Under Uncertainty U(Rs. 45) > EU risk-aversion. 12 U(Rs. 45) MU declines as wealth rises. EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
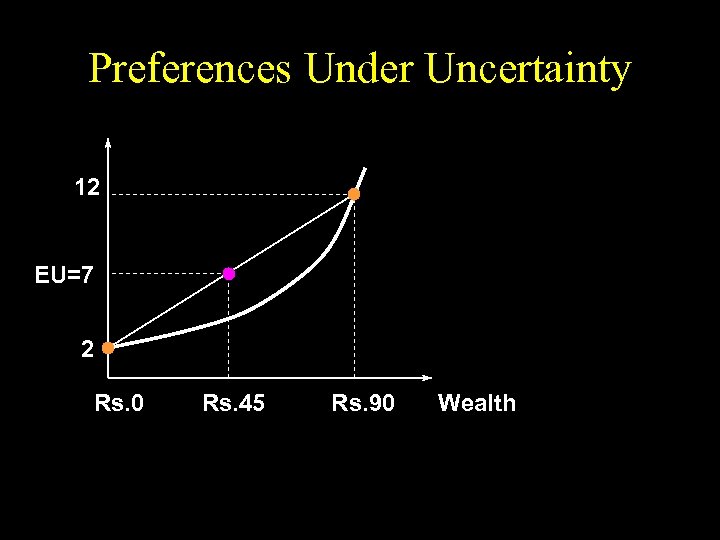 Preferences Under Uncertainty 12 EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
Preferences Under Uncertainty 12 EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
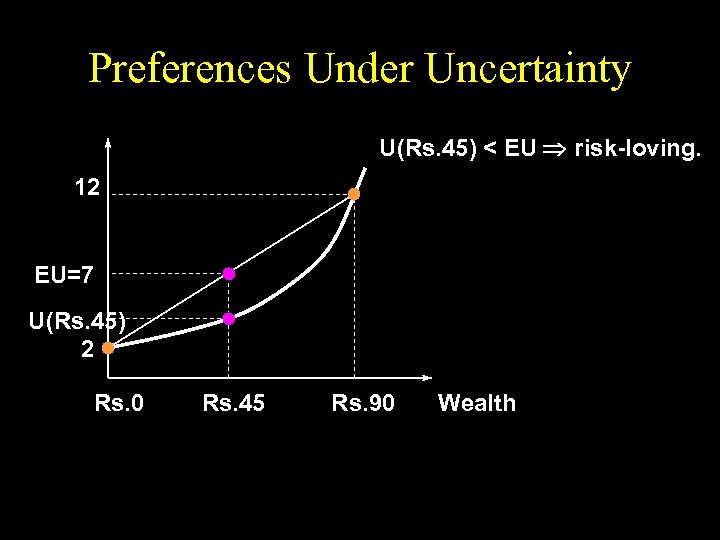 Preferences Under Uncertainty U(Rs. 45) < EU risk-loving. 12 EU=7 U(Rs. 45) 2 Rs. 0 Rs. 45 Rs. 90 Wealth
Preferences Under Uncertainty U(Rs. 45) < EU risk-loving. 12 EU=7 U(Rs. 45) 2 Rs. 0 Rs. 45 Rs. 90 Wealth
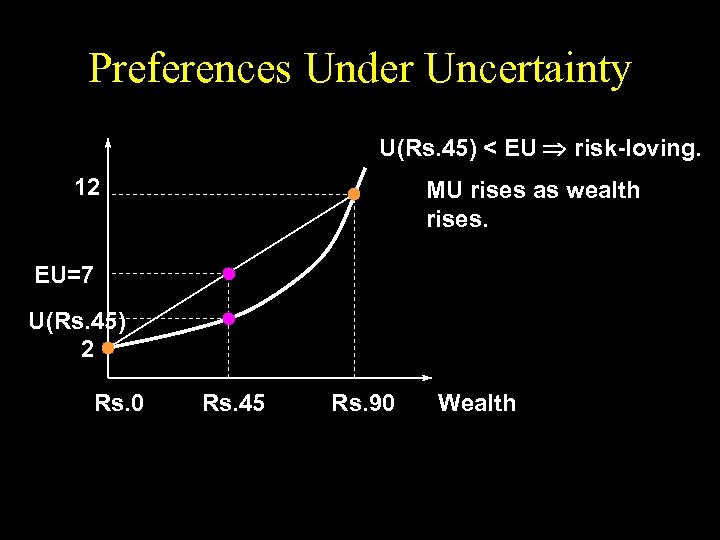 Preferences Under Uncertainty U(Rs. 45) < EU risk-loving. 12 MU rises as wealth rises. EU=7 U(Rs. 45) 2 Rs. 0 Rs. 45 Rs. 90 Wealth
Preferences Under Uncertainty U(Rs. 45) < EU risk-loving. 12 MU rises as wealth rises. EU=7 U(Rs. 45) 2 Rs. 0 Rs. 45 Rs. 90 Wealth
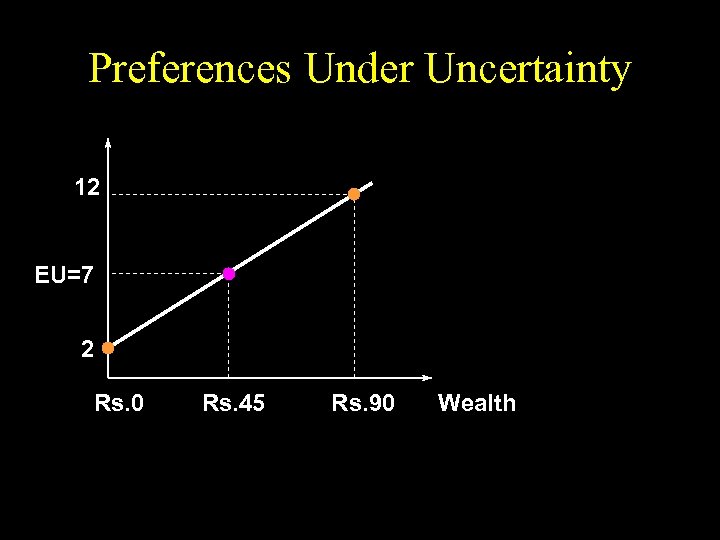 Preferences Under Uncertainty 12 EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
Preferences Under Uncertainty 12 EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
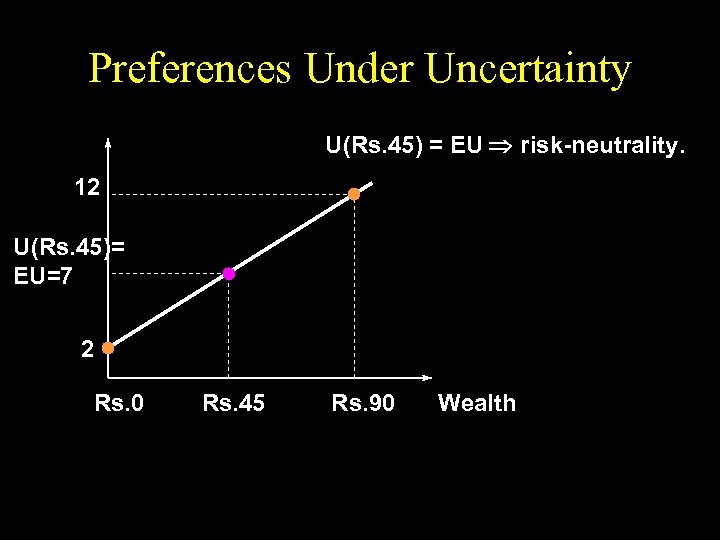 Preferences Under Uncertainty U(Rs. 45) = EU risk-neutrality. 12 U(Rs. 45)= EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
Preferences Under Uncertainty U(Rs. 45) = EU risk-neutrality. 12 U(Rs. 45)= EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
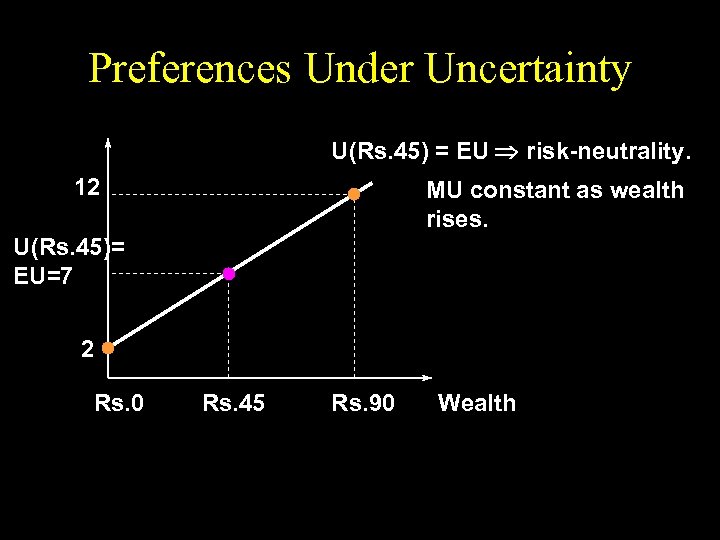 Preferences Under Uncertainty U(Rs. 45) = EU risk-neutrality. 12 MU constant as wealth rises. U(Rs. 45)= EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
Preferences Under Uncertainty U(Rs. 45) = EU risk-neutrality. 12 MU constant as wealth rises. U(Rs. 45)= EU=7 2 Rs. 0 Rs. 45 Rs. 90 Wealth
 Preferences Under Uncertainty u State-contingent consumption plans that give equal expected utility are equally preferred.
Preferences Under Uncertainty u State-contingent consumption plans that give equal expected utility are equally preferred.
 Preferences Under Uncertainty Cna Indifference curves EU 1 < EU 2 < EU 3 EU 2 EU 1 Ca
Preferences Under Uncertainty Cna Indifference curves EU 1 < EU 2 < EU 3 EU 2 EU 1 Ca
 Preferences Under Uncertainty u What is the MRS of an indifference curve? u Get consumption c 1 with prob. 1 and c 2 with prob. 2 ( 1 + 2 = 1). u EU = 1 U(c 1) + 2 U(c 2). u For constant EU, d. EU = 0.
Preferences Under Uncertainty u What is the MRS of an indifference curve? u Get consumption c 1 with prob. 1 and c 2 with prob. 2 ( 1 + 2 = 1). u EU = 1 U(c 1) + 2 U(c 2). u For constant EU, d. EU = 0.
 Preferences Under Uncertainty
Preferences Under Uncertainty
 Preferences Under Uncertainty
Preferences Under Uncertainty
 Preferences Under Uncertainty
Preferences Under Uncertainty
 Preferences Under Uncertainty
Preferences Under Uncertainty
 Preferences Under Uncertainty
Preferences Under Uncertainty
 Preferences Under Uncertainty Cna Indifference curves EU 1 < EU 2 < EU 3 EU 2 EU 1 Ca
Preferences Under Uncertainty Cna Indifference curves EU 1 < EU 2 < EU 3 EU 2 EU 1 Ca
 Choice Under Uncertainty u Q: How is a rational choice made under uncertainty? u A: Choose the most preferred affordable state-contingent consumption plan.
Choice Under Uncertainty u Q: How is a rational choice made under uncertainty? u A: Choose the most preferred affordable state-contingent consumption plan.
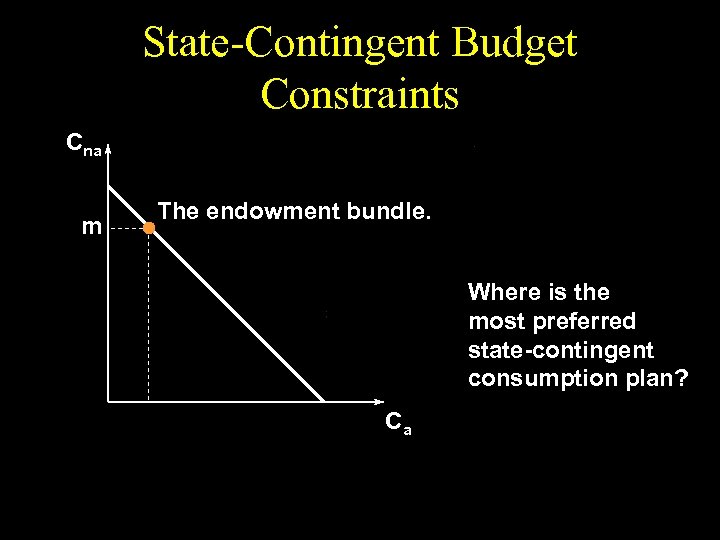 State-Contingent Budget Constraints Cna m The endowment bundle. Where is the most preferred state-contingent consumption plan? Ca
State-Contingent Budget Constraints Cna m The endowment bundle. Where is the most preferred state-contingent consumption plan? Ca
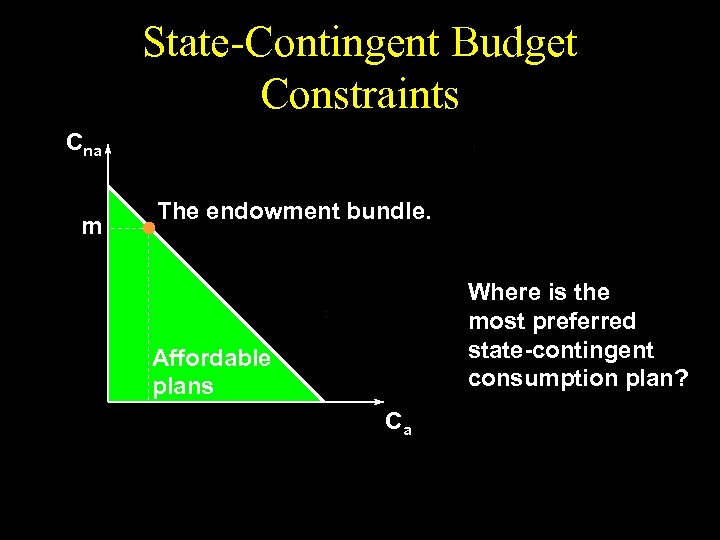 State-Contingent Budget Constraints Cna m The endowment bundle. Where is the most preferred state-contingent consumption plan? Affordable plans Ca
State-Contingent Budget Constraints Cna m The endowment bundle. Where is the most preferred state-contingent consumption plan? Affordable plans Ca
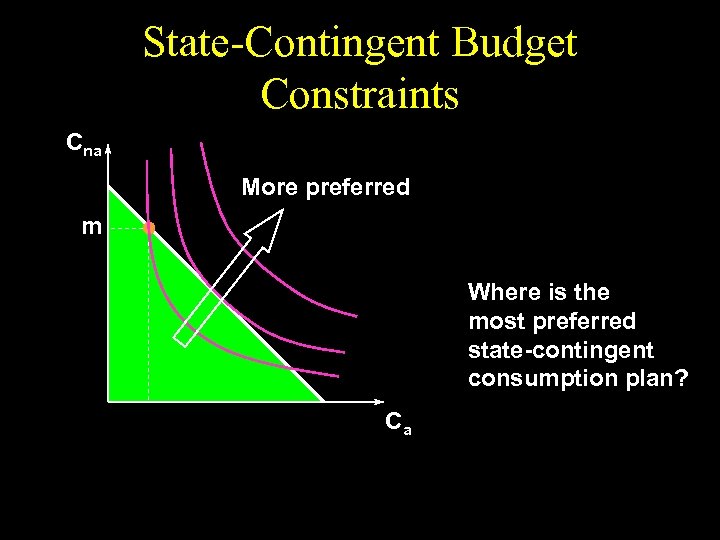 State-Contingent Budget Constraints Cna More preferred m Where is the most preferred state-contingent consumption plan? Ca
State-Contingent Budget Constraints Cna More preferred m Where is the most preferred state-contingent consumption plan? Ca
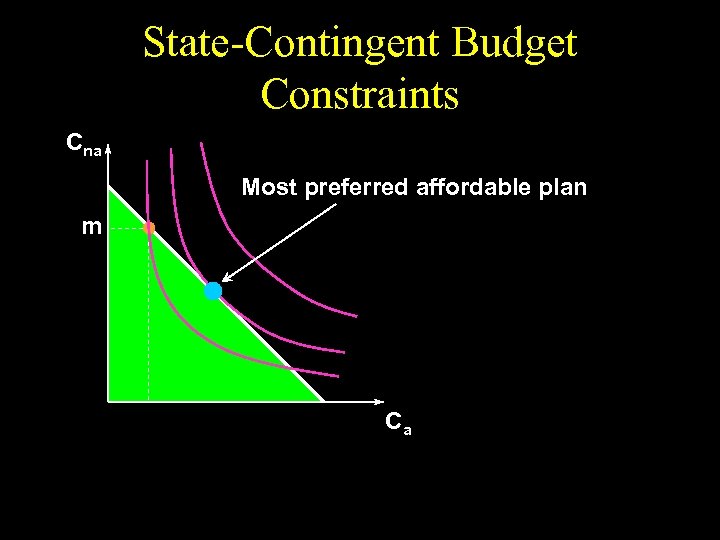 State-Contingent Budget Constraints Cna Most preferred affordable plan m Ca
State-Contingent Budget Constraints Cna Most preferred affordable plan m Ca
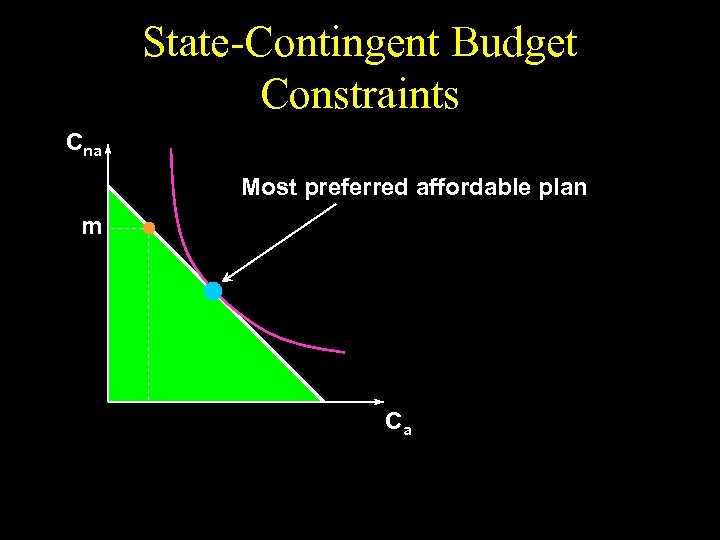 State-Contingent Budget Constraints Cna Most preferred affordable plan m Ca
State-Contingent Budget Constraints Cna Most preferred affordable plan m Ca
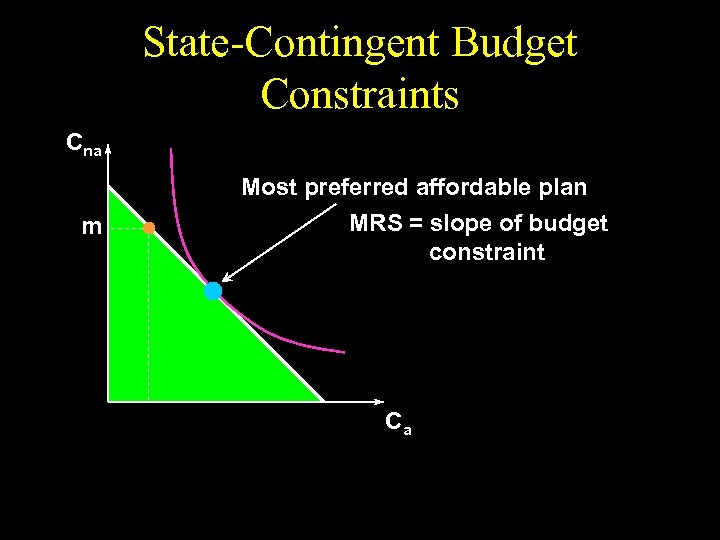 State-Contingent Budget Constraints Cna m Most preferred affordable plan MRS = slope of budget constraint Ca
State-Contingent Budget Constraints Cna m Most preferred affordable plan MRS = slope of budget constraint Ca
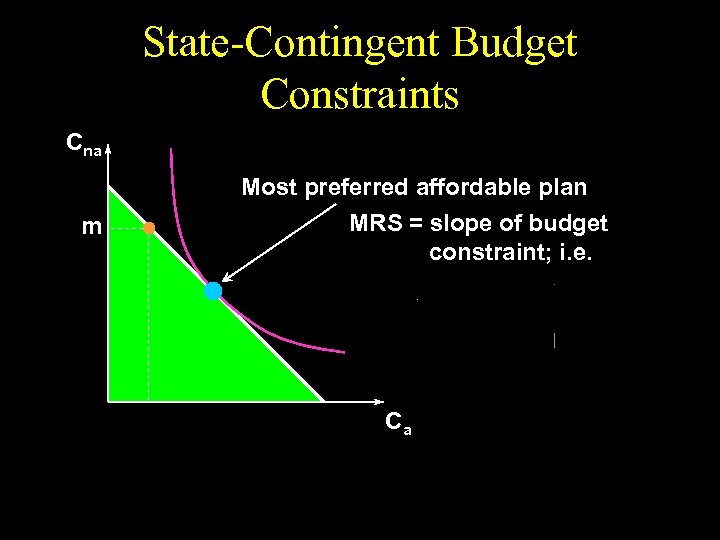 State-Contingent Budget Constraints Cna m Most preferred affordable plan MRS = slope of budget constraint; i. e. Ca
State-Contingent Budget Constraints Cna m Most preferred affordable plan MRS = slope of budget constraint; i. e. Ca
 Competitive Insurance u Suppose entry to the insurance industry is free. u Expected economic profit = 0. u I. e. K - a. K - (1 - a)0 = ( - a)K = 0. u I. e. free entry = a. u If price of Rs. 1 insurance = accident probability, then insurance is fair.
Competitive Insurance u Suppose entry to the insurance industry is free. u Expected economic profit = 0. u I. e. K - a. K - (1 - a)0 = ( - a)K = 0. u I. e. free entry = a. u If price of Rs. 1 insurance = accident probability, then insurance is fair.
 Competitive Insurance u When insurance is fair, rational insurance choices satisfy
Competitive Insurance u When insurance is fair, rational insurance choices satisfy
 Competitive Insurance u When insurance is fair, rational insurance choices satisfy u I. e.
Competitive Insurance u When insurance is fair, rational insurance choices satisfy u I. e.
 Competitive Insurance u When insurance is fair, rational insurance choices satisfy u I. e. u Marginal utility of income must be the same in both states.
Competitive Insurance u When insurance is fair, rational insurance choices satisfy u I. e. u Marginal utility of income must be the same in both states.
 Competitive Insurance u How much fair insurance does a riskaverse consumer buy?
Competitive Insurance u How much fair insurance does a riskaverse consumer buy?
 Competitive Insurance u How much fair insurance does a riskaverse consumer buy? u Risk-aversion MU(c) as c .
Competitive Insurance u How much fair insurance does a riskaverse consumer buy? u Risk-aversion MU(c) as c .
 Competitive Insurance u How much fair insurance does a riskaverse consumer buy? u Risk-aversion u Hence MU(c) as c .
Competitive Insurance u How much fair insurance does a riskaverse consumer buy? u Risk-aversion u Hence MU(c) as c .
 Competitive Insurance u How much fair insurance does a riskaverse consumer buy? u Risk-aversion MU(c) as c . u Hence u I. e. full-insurance.
Competitive Insurance u How much fair insurance does a riskaverse consumer buy? u Risk-aversion MU(c) as c . u Hence u I. e. full-insurance.
 “Unfair” Insurance u Suppose insurers make positive expected economic profit. u I. e. K - a. K - (1 - a)0 = ( - a)K > 0.
“Unfair” Insurance u Suppose insurers make positive expected economic profit. u I. e. K - a. K - (1 - a)0 = ( - a)K > 0.
 “Unfair” Insurance u Suppose insurers make positive expected economic profit. u I. e. K - a. K - (1 - a)0 = ( - a)K > 0. u Then > a
“Unfair” Insurance u Suppose insurers make positive expected economic profit. u I. e. K - a. K - (1 - a)0 = ( - a)K > 0. u Then > a
 “Unfair” Insurance u Rational choice requires
“Unfair” Insurance u Rational choice requires
 “Unfair” Insurance u Rational u Since choice requires
“Unfair” Insurance u Rational u Since choice requires
 “Unfair” Insurance u Rational choice requires u Since u Hence for a risk-averter.
“Unfair” Insurance u Rational choice requires u Since u Hence for a risk-averter.
 “Unfair” Insurance u Rational choice requires u Since u Hence for a risk-averter. u I. e. a risk-averter buys less than full “unfair” insurance.
“Unfair” Insurance u Rational choice requires u Since u Hence for a risk-averter. u I. e. a risk-averter buys less than full “unfair” insurance.
 Uncertainty is Pervasive u What are rational responses to uncertainty? – buying insurance (health, life, auto) – a portfolio of contingent consumption goods.
Uncertainty is Pervasive u What are rational responses to uncertainty? – buying insurance (health, life, auto) – a portfolio of contingent consumption goods.
 Uncertainty is Pervasive u What are rational responses to uncertainty? – buying insurance (health, life, auto) – a portfolio of contingent consumption goods.
Uncertainty is Pervasive u What are rational responses to uncertainty? – buying insurance (health, life, auto) – a portfolio of contingent consumption goods.
 Uncertainty is Pervasive u What are rational responses to uncertainty? – buying insurance (health, life, auto) ? – a portfolio of contingent consumption goods.
Uncertainty is Pervasive u What are rational responses to uncertainty? – buying insurance (health, life, auto) ? – a portfolio of contingent consumption goods.
 Diversification u Two firms, A and B. Shares cost Rs. 10. u With prob. 1/2 A’s profit is Rs. 100 and B’s profit is Rs. 20. u With prob. 1/2 A’s profit is Rs. 20 and B’s profit is Rs. 100. u You have Rs. 100 to invest. How?
Diversification u Two firms, A and B. Shares cost Rs. 10. u With prob. 1/2 A’s profit is Rs. 100 and B’s profit is Rs. 20. u With prob. 1/2 A’s profit is Rs. 20 and B’s profit is Rs. 100. u You have Rs. 100 to invest. How?
 Diversification u Buy only firm A’s stock? u Rs. 100/10 = 10 shares. u You earn Rs. 1000 with prob. 1/2 and Rs. 200 with prob. 1/2. u Expected earning: Rs. 500 + Rs. 100 = Rs. 600
Diversification u Buy only firm A’s stock? u Rs. 100/10 = 10 shares. u You earn Rs. 1000 with prob. 1/2 and Rs. 200 with prob. 1/2. u Expected earning: Rs. 500 + Rs. 100 = Rs. 600
 Diversification u Buy only firm B’s stock? u Rs. 100/10 = 10 shares. u You earn Rs. 1000 with prob. 1/2 and Rs. 200 with prob. 1/2. u Expected earning: Rs. 500 + Rs. 100 = Rs. 600
Diversification u Buy only firm B’s stock? u Rs. 100/10 = 10 shares. u You earn Rs. 1000 with prob. 1/2 and Rs. 200 with prob. 1/2. u Expected earning: Rs. 500 + Rs. 100 = Rs. 600
 Diversification u Buy 5 shares in each firm? u You earn Rs. 600 for sure. u Diversification has maintained expected earning and lowered risk.
Diversification u Buy 5 shares in each firm? u You earn Rs. 600 for sure. u Diversification has maintained expected earning and lowered risk.
 Diversification u Buy 5 shares in each firm? u You earn Rs. 600 for sure. u Diversification has maintained expected earning and lowered risk. u Typically, diversification lowers expected earnings in exchange for lowered risk.
Diversification u Buy 5 shares in each firm? u You earn Rs. 600 for sure. u Diversification has maintained expected earning and lowered risk. u Typically, diversification lowers expected earnings in exchange for lowered risk.
 Risk Spreading/Mutual Insurance u 100 risk-neutral persons each independently risk a Rs. 10, 000 loss. u Loss probability = 0. 01. u Initial wealth is Rs. 40, 000. u No insurance: expected wealth is
Risk Spreading/Mutual Insurance u 100 risk-neutral persons each independently risk a Rs. 10, 000 loss. u Loss probability = 0. 01. u Initial wealth is Rs. 40, 000. u No insurance: expected wealth is
 Risk Spreading/Mutual Insurance u Mutual insurance: Expected loss is u Each of the 100 persons pays Rs. 1 into a mutual insurance fund. u Mutual insurance: expected wealth is u Risk-spreading benefits everyone.
Risk Spreading/Mutual Insurance u Mutual insurance: Expected loss is u Each of the 100 persons pays Rs. 1 into a mutual insurance fund. u Mutual insurance: expected wealth is u Risk-spreading benefits everyone.


