Topic 3 The Time Value of Money Chapter

Topic 3 The Time Value of Money Chapter Organization 3. 1. Future Value and Compounding 3. 2. Present Value and Discounting 3. 3. More on Present and Future Values 3. 4. Present and Future Values of Multiple Cash Flows 3. 5. Valuing Level Cash Flows: Annuities and Perpetuities 3. 6. Comparing Rates: The Effect of Compounding 3. 7. Loan Types and Loan Amortization 1

3. 1. Future Value and Compounding The future value (FV) is the cash value of an investment at some time in the future Suppose you invest € 100 in a saving account that pays 10% interest per year. How much will you have in one year? 2

3. 1. Future Value and Compounding The future value (FV) is the cash value of an investment at some time in the future. Suppose you invest € 100 in a saving account that pays 10% interest per year. How much will you have in one year? € 110 100 x 1, 1 = € 110 (1+r) r – an interest rate 3

3. 1. Future Value and Compounding If you leave € 110 in bank for the next year, how much will you have in two years? € 121 = € 110 x 1, 1 These € 121 consists of four parts: € 100 — the original principal € 10 — 10% interest you earned the first year € 10 — 10% interest you earned the second year € 1 — interest you earned the second year on the interest paid the first year 4

3. 1. Future Value and Compounding The compound interest means earning interest on interest. The simple interest is the interest which is not reinvested and it is earned each period only on the original principal. 5

3. 1. Future Value and Compounding Now take a closer look at how we calculated the € 121 future value. € 121 = € 110 x 1, 1= € 100 x 1, 1 = = € 100 x 1, 12 If we invest € 121 for one year again we will have € 133, 10 = € 121 x 1, 1 = € 100 x 1, 13 Future value = € 100 x (1+r)t 6

3. 1. Future Value and Compounding Future value = € 100 x (1+r)t — future value interest factor What would your 100 be worth after five years? FV =€ 100 x(1+0, 1)5 = 100 x 1, 6105 =161, 05 1, 1 yx 5 = 1, 6105 7

3. 1. Future Value and Compounding Future value = € 100 x (1+r)t 8

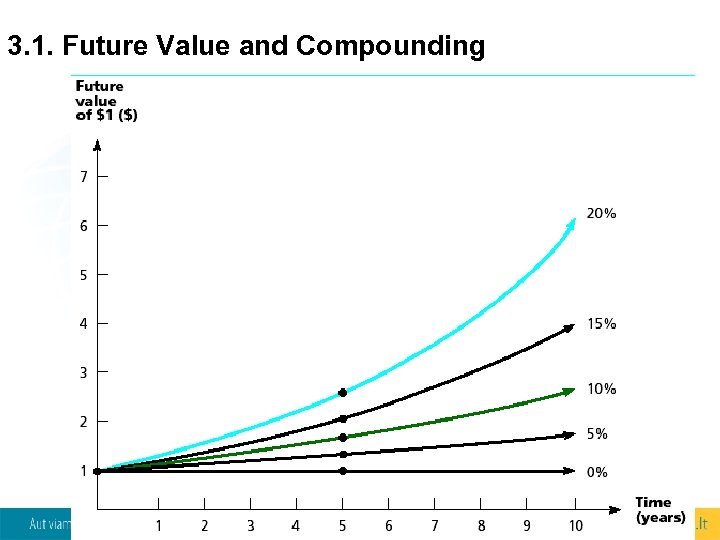3. 1. Future Value and Compounding 9

3. 2. Present Value and Discounting How much do we have to invest today at 10% to get € 100 in one year? FV = € 100 x (1+r)t € 100 = Present value x (1+0, 1)1 € 100 Present value = ——— = € 90, 909 1, 1 10

3. 2. Present Value and Discounting To discount means to calculate the present value of some future amount 1 / (1+r)t — discount factor 11

3. 2. Present Value and Discounting Suppose you need to have € 1. 000 in two years. If you can earn 7%, how much do you have to invest to make sure that you have the € 1. 000 when you need it? € 1. 000 = PV x 1, 072 PV = € 1. 000 / 1, 1449 = € 873, 44 1, 07 yx 2 1/x x 1000 = 873, 44 12

3. 3. More on Present and Future Values FVt = PV x (1+r)t PV = FVt / (1+r)t Your company proposes to buy an asset for € 335. This investment is very safe. You would sell off the asset in three years for € 400. You know you could invest the $335 elsewhere at 10 percent with very little risk. What do you think of the proposed investment? 13

3. 3. More on Present and Future Values FVt = PV x (1+r)t FV = € 335 x 1, 13 = € 335 x 1, 331 = € 445, 89 This is not a good investment. How much should you invest in order to make this investment be as good as the other one? PV = FVt / (1+r)t PV= € 400 / (1+0, 1)3 = 400 / 1, 331 =€ 300, 53 14

3. 3. More on Present and Future Values FVt = PV x (1+r)t PV = FVt / (1+r)t Determining the Discount Rate r We are offered an investment that costs us € 1. 000 and will double our money in eight years. To compare this to other investments, we would like to know what discount rate is implicit in these numbers? 15

3. 3. More on Present and Future Values FVt = PV x (1+r)t € 2. 000 = € 1. 000 x (1+r)8 2 = (1+r)8 8 √ 2 = 1+r 21/8 = 1+r 1, 090508 = 1+r r = 9, 0508% 16

3. 3. More on Present and Future Values The Rule of 72. For reasonable rates of return, the time it takes to double your money is given approximately by 72 / r%. t ≈ 72/r% 8 ≈ 72/r% r ≈ 72/8 ≈ 9% This rule is fairly accurate for discount rates in the range of 5 percent to 20 percent. 17

3. 3. More on Present and Future Values Finding the number of periods t Suppose we are interested in purchasing an asset that costs € 50, 000. We currently have € 25, 000. If we can earn 12 percent on this € 25, 000, how long will it take to have € 50, 000? t ≈ 72/r% t ≈ 72/12% ≈ 6 years 18

3. 3. More on Present and Future Values FVt = PV x (1+r)t € 50. 000 = € 25. 000 x (1+0, 12)t = 2 log 1, 12 t = log 2 t x log 1, 12 = log 2 t = log 2 / log 1, 12 t = 0, 301029 / 0, 049218 = 6, 11625 years 19

3. 4. Present and Future Values of Multiple Cash Flows 0 1 100 x 1, 08 +108 2 x 1, 08 224, 64 20

3. 4. Present and Future Values of Multiple Cash Flows 0 1 100 x 1, 08 2 x 1, 08 116, 64 108 224, 64 21

3. 4. Present and Future Values of Multiple Cash Flows Based on this example, there are two ways to calculate future values of multiple cash flows: 1. compound the accumulated balance forward one year at a time or 2. calculate the future value of each cash flow first and then add them up 0 1 2 2. 000 3 4 2. 000 5 22 2. 000

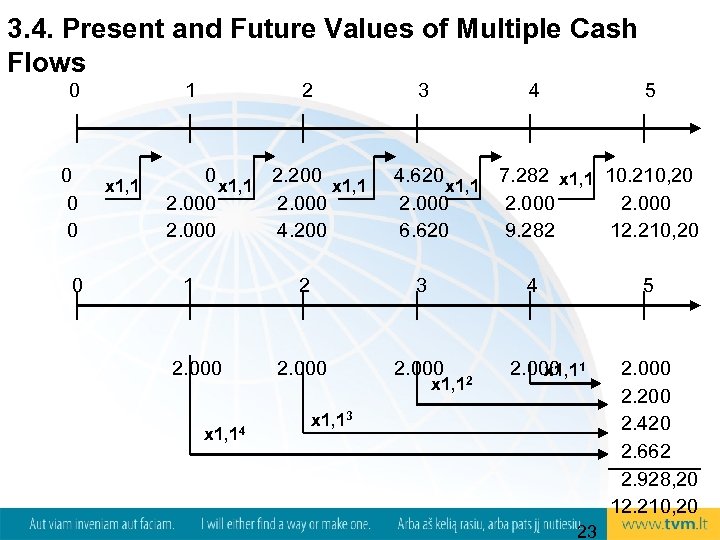3. 4. Present and Future Values of Multiple Cash Flows 0 0 0 1 x 1, 1 2 0 x 1, 1 2. 200 x 1, 1 2. 000 4. 200 1 3 4 4. 620 x 1, 1 7. 282 x 1, 1 10. 210, 20 2. 000 6. 620 9. 282 12. 210, 20 2 2. 000 x 1, 14 5 3 4 2. 000 x 1, 12 5 2. 000 1 x 1, 13 23 2. 000 2. 200 2. 420 2. 662 2. 928, 20 12. 210, 20

3. 4. Present and Future Values of Multiple Cash Flows Suppose you need 1. 000 in one year and 2. 000 in two years. If you can earn 9% on your money, how big should be the initial sum to exactly cover these amounts in the future 0 1 2 x 1 1, 091 1. 000 1 x 1, 092 2. 000 24

3. 4. Present and Future Values of Multiple Cash Flows 2. 000 / 1, 092 = 1. 683, 36 1. 000 / 1, 091 = 917. 43 1. 683, 36 + 917, 43 = 2. 600, 79 We can check our answer 2. 600, 79 x 1, 09 = 2. 834, 86 – 1. 000 = 1. 834, 86 x 1, 09 = 2. 000 25

3. 4. Present and Future Values of Multiple Cash Flows You are offered an investment that will pay you 200 in one year, 400 the second year, 600 the third year, and 800 at the end of the fourth year. You can earn 12% on very similar investments. What is the most you should pay for this one? 0 1 2 3 4 200 400 600 800 26

3. 4. Present and Future Values of Multiple Cash Flows 0 1 2 3 4 200 400 600 800 200 x 1/1, 121 = 200/1, 1200 = 178, 57 400 x 1/1, 122 = 400/1, 2544 = 318, 88 600 x 1/1, 123 = 600/1, 4049 = 427, 07 800 x 1/1, 124 = 800/1, 5735 = 508, 41 Total present value = 1. 432, 93 27

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities A series of constant or level cash flows that occur at the end of each period for some fixed number of periods is called an ordinary annuity. Suppose we were examining an asset that promised to pay 500 at the end of each of the next three years. If we wanted to earn 10% on our money, how much would we offer for this annuity? 28

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities 0 1 2 3 500 500 PV = (500/1, 11)+(500/1, 12)+(500/1, 13) = = 454, 55 + 413, 22 + 375, 66 = 1. 243, 43 29

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities The present value of an annuity of C period for t periods when the rate of return or interest is r given by: An. PV = C x {1 -[1/(1+r)t]}/r = = 500 x{1 -[1/(1+0, 1)3]}/0, 1 = 500 x[1–(1/1, 331)]/0, 1= = 500 x (1 -0, 75131)/0, 1 = 500 x 2, 48685 = 1. 243, 43 30

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities You have determined you can afford to pay € 632 per month towards a new car. You call up your local bank and find out that the going rate is 1% per month for 48 months. How much can you borrow? An. PV = C x {1 -[1/(1+r)t]}/r = = 632 x {1 - [1/(1+0, 01)48]}/0, 01 = = 632 x [ 1 -(1/1, 61223)]/0, 01 = = 632 x(1 -0, 6203)/0, 01 = 632 x 37, 9740 = = € 24. 000 31

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities Finding the payment. Suppose you wish to start up a new business. To produce and market your product you need to borrow 100. 000. You propose to pay off the loan quickly by making five equal annual payments. If the interest rate is 18%, what will the payment be? An. PV = C x {1 -[1/(1+r)t]}/r 100. 000 = C x {1 - [1/(1+0, 18)5]}/0, 18 100. 000 = C x (1 -0, 4371)/0, 18 100. 000 = C x 3, 1272 C = 100. 000 / 3, 1272 = 31. 977 32

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities Finding the Number of Payments. You ran a little short on your vocation, so you put € 1. 000 on your credit card. You can only afford to make the minimum payment of € 20 per month. The interest rate on the credit card is 1, 5% per month. How long will you need to pay off the € 1. 000? An. PV = C x {1 -[1/(1+r)t]}/r 1000 = 20 x {1 - [1/(1+0, 015)t]}/0, 015 33

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities 1000/20 x 0, 015 = 1 - 1/(1+0, 015)t 0, 75 -1 = - 1/(1, 015)t 0, 25 = 1/(1, 015)t ¼ = 1/1, 015 t = 4 log 1, 015 t = log 4 t x log 1, 015 = log 4 t = log 4 / log 1, 015 = = 0, 60206 / 0, 006466 = 93, 11 34

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities Finding the Rate. An insurance company offers to pay you € 1. 000 per year for 4 years if you pay € 3. 000 up front. What rate is implicit in this 4 -year annuity? An. PV = C x {1 -[1/(1+r)t]}/r 3. 000 = 1. 000 x {1 - [1/(1+r)4]}/r then r=10% 1. 000 x {1 - [1/(1+0, 1)4]}/0, 1 = 3. 169, 90 35

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities 3. 000 = 1. 000 x {1 - [1/(1+r)4]}/r then r = 12% 1. 000 x{1 - [1/(1+0, 12)4]}/0, 12= 3. 037, 35 Then r = 13% 1. 000 x{1 - [1/(1+0, 13)4]}/0, 13= 2. 974, 47 r = 12, 59% 36

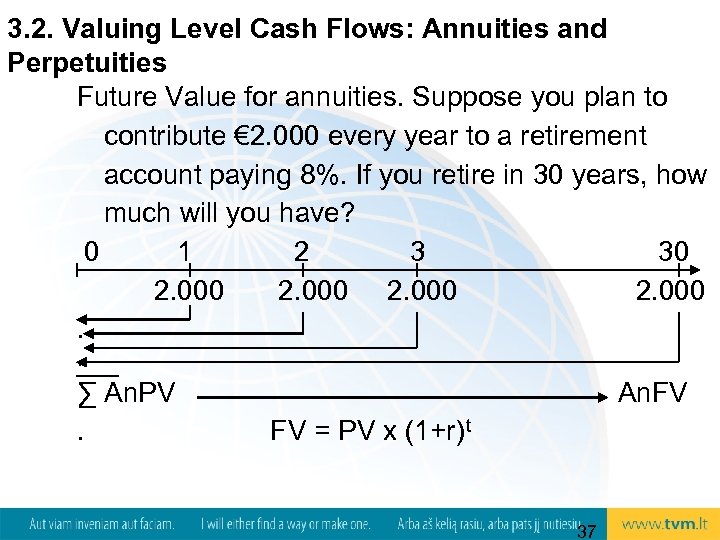3. 2. Valuing Level Cash Flows: Annuities and Perpetuities Future Value for annuities. Suppose you plan to contribute € 2. 000 every year to a retirement account paying 8%. If you retire in 30 years, how much will you have? 0 1 2 3 30 2. 000. . ∑ An. PV. An. FV FV = PV x (1+r) t 37

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities An. PV = C x {1 -[1/(1+r)t]}/r An. PV=2. 000 x{1 -[1/(1+0, 08)30]}/0, 08 An. PV = 2. 000 x [1 - 0, 0994)]/0, 08 = = 22. 515, 57 An. FV = 22. 515, 57 x (1+ 0, 08)30 = = 22. 515, 57 x 10, 063 = 226. 566, 46 38

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities An. FV = An. PV x (1+r)t = = C x {1 -[1/(1+r)t]}/r x (1+r)t = An. FV = C x {(1+r)t - 1}/r 39

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities An. FV = C x {(1+r)t - 1}/r An. FV= 2. 000 x{(1+0, 08)30 -1}/0, 08 An. FV = 2. 000 x (10, 0627 -1)/0, 08 = An. FV=2. 000 x 113, 2832 = 226. 566, 46 40

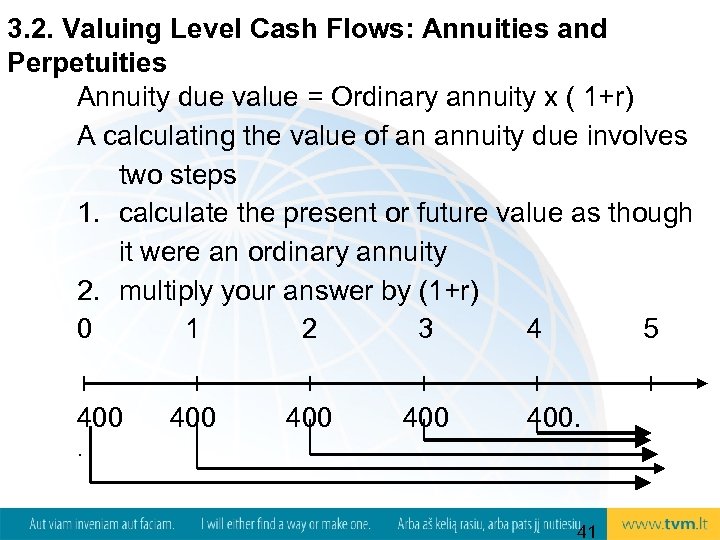3. 2. Valuing Level Cash Flows: Annuities and Perpetuities Annuity due value = Ordinary annuity x ( 1+r) A calculating the value of an annuity due involves two steps 1. calculate the present or future value as though it were an ordinary annuity 2. multiply your answer by (1+r) 0 1 2 3 4 5 400 400 400. . 41

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities r = 10% An. FV = 400 x 1, 15+ 400 x 1, 14+ 400 x 1, 13+ 400 x 1, 12+ 400 x 1, 11= = 440, 00 +484, 00 +532, 400 + 585, 64 + + 644, 204 = 2. 686, 244 An. FV = C x {(1+r)t - 1}/r x (1+r) An. FV = {400 x [(1+0, 1)5 – 1]/0, 10} x 1, 1= = 2. 686, 244 42

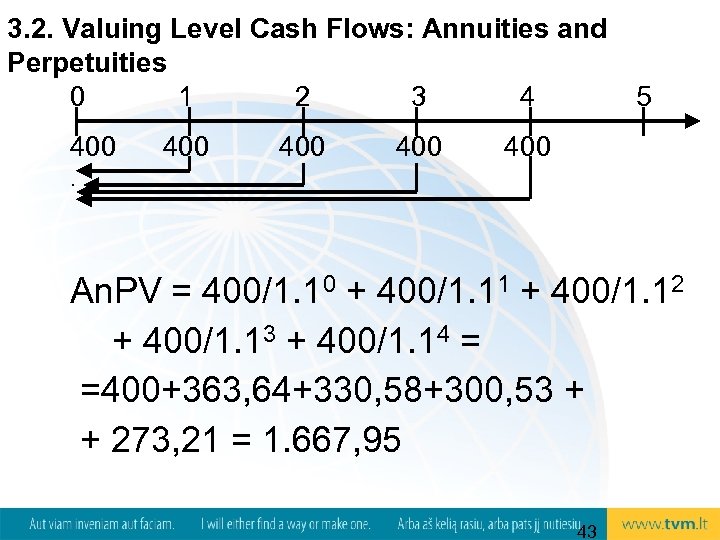3. 2. Valuing Level Cash Flows: Annuities and Perpetuities 0 1 2 3 4 400 400 5 400 . An. PV = 400/1. 10 + 400/1. 11 + 400/1. 12 + 400/1. 13 + 400/1. 14 = =400+363, 64+330, 58+300, 53 + + 273, 21 = 1. 667, 95 43

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities An. PV = C x {1 -[1/(1+r)t]}/r x (1+r) An. PV=400 x{1–[1/(1+0, 1)5]}/0, 1 x x (1+0, 1) = 400 x 3, 7908/0, 1 x 1, 1= = 1. 516, 32 x 1, 1 = 1. 667, 95 44

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities. A perpetuity is an annuity in which the cash flows continue forever. ì é 1 ùü í 1 - ê ¥ úý 1 î ë ( + r ) ûþ = Perp. PV C r 45

3. 2. Valuing Level Cash Flows: Annuities and Perpetuities PV for a perpetuity = C / r An investment offers a perpetual cash flow of 500 every year. The return you require on such investment is 8%. What is the value of this investment? PV for a perpetuity = C/r = = 500/0, 08 = 6. 250 46

3. 3. Comparing Rates: The Effect of Compounding If a rate is quoted as 10% compounded semiannually, then it means that the investment actually pays 5% every six months. A natural question then arises: Is 5% every six months the same thing as 10% per year? 100 x 1, 052 = 110, 25 Annual interest rate = 10, 25% 47

3. 3. Comparing Rates: The Effect of Compounding The 10% is called a stated, quoted interest rate, or annual percentage rate (APR) The 10, 25% is called the effective annual rate (EAR) 48

3. 3. Comparing Rates: The Effect of Compounding Bank A: 15% compounded daily Bank B: 15, 5% compounded quarterly Bank C: 16% compounded annually Which of these is the best if you are thinking of opening a savings account? The EAR of Bank C is 16% 49

3. 3. Comparing Rates: The Effect of Compounding Bank B is actually paying 0, 155/4 = 0, 03875 or 3, 875% per quarter An investment of 100 for four quarters would grow to: 100 x 1, 038754 = 116, 42 EAR = 16. 42% Bank A has a daily interest rate 0, 15/365 = 0, 000411 or 0, 0411% daily 100 x 1, 000411365 = 116, 18 EAR = 16, 18% 50

3. 3. Comparing Rates: The Effect of Compounding EAR = [ 1+ (APR/m )]m – 1 where m is the number of times the interest is compounded during the year APR is annual percentage rate EAR is effective annual rate For example, 12% is compounded monthly EAR = [ 1 + (0, 12 / 12)]12 -1 = 1, 0112 -1 = = 1, 126825 -1 = 12, 6825% 51

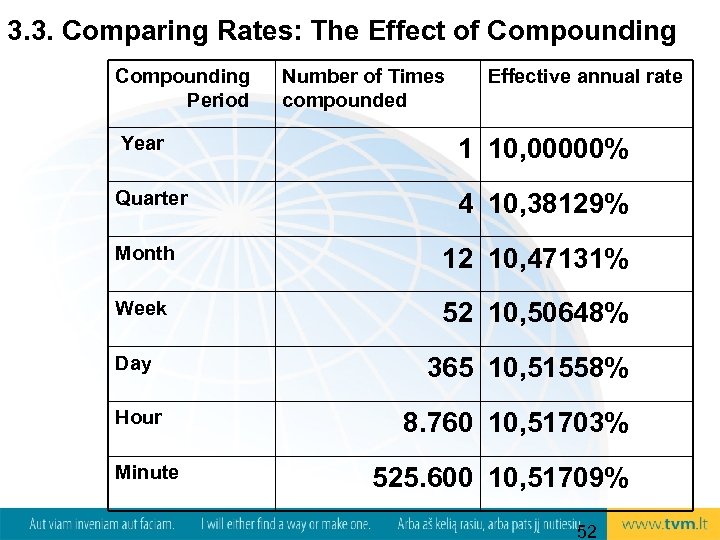3. 3. Comparing Rates: The Effect of Compounding Period Number of Times compounded Effective annual rate Year 1 10, 00000% Quarter 4 10, 38129% Month 12 10, 47131% Week 52 10, 50648% Day Hour Minute 365 10, 51558% 8. 760 10, 51703% 525. 600 10, 51709% 52

3. 3. Comparing Rates: The Effect of Compounding EAR = e APR -1 where e is the number 2, 71828 EAR = 2, 718280, 10 -1 = 1, 1051709 - 1= = 0, 1051709 or 10, 51709% 53

3. 4. Loan Types and Loan Amortization Three basic types of loans are: • pure discount loans • interest-only loans • amortized loans 54

6. 4. Loan Types and Loan Amortization Pure discount loan is the loan when the borrower receives money today and repays a single lump sum at some time in the future. 0 14. 186 1 2 x 1, 125 3 4 5 = 25. 000 where r = 12% 55

6. 4. Loan Types and Loan Amortization Interest-only loan repayment plan calls for the borrower to pay interest each period and to repay the entire principal (the original loan amount) at some point in the future. 0 1 2 3 1. 000 100 where r = 10% 100 1. 100 56

6. 4. Loan Types and Loan Amortization The process of providing for a loan to be paid off by making regular principal reductions is called amortizing the loan. • A simple way of amortizing a loan is to have the borrower pay the interest each period plus some fixed amount. • The most common way of amortizing a loan is to have the borrower make a single, fixed payment every period. 57

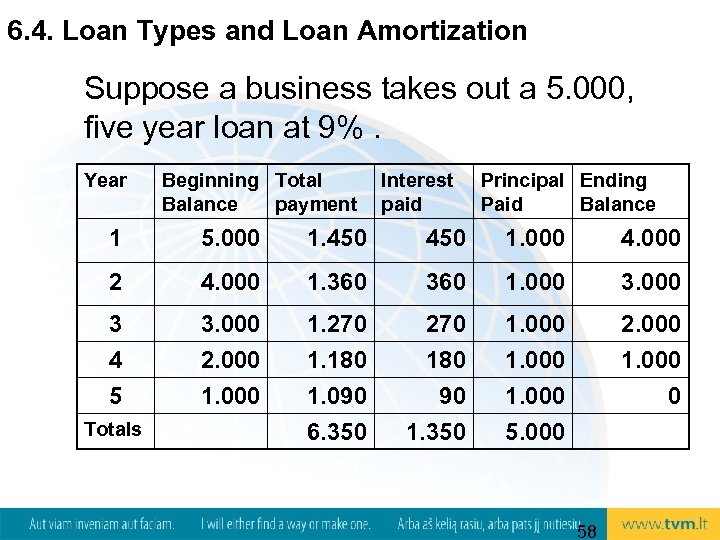6. 4. Loan Types and Loan Amortization Suppose a business takes out a 5. 000, five year loan at 9%. Year Beginning Total Balance payment Interest paid Principal Ending Paid Balance 1 5. 000 1. 450 1. 000 4. 000 2 4. 000 1. 360 1. 000 3 3. 000 1. 270 1. 000 2. 000 4 2. 000 1. 180 1. 000 5 1. 000 1. 090 90 1. 000 0 6. 350 1. 350 5. 000 Totals 58

6. 4. Loan Types and Loan Amortization An. PV = C x {1 -[1/(1+r)t]}/r 5. 000 = C x {1 - [1/(1+0, 09)5]}/0, 09 5. 000 = C x (1 -0, 6499)/0, 09 5. 000 = C x 3, 8897 C = 5. 000 / 3, 8897 = 1. 285, 46 59

6. 4. Loan Types and Loan Amortization Year Beginning Balance Total payment Interest paid Principal Paid Ending Balance 1 5. 000, 00 1. 285, 46 450, 00 835, 46 4. 164, 54 2 4. 164, 54 1. 285, 46 374, 81 910, 35 3. 253, 88 3 3. 253, 88 1. 285, 46 292, 85 992, 61 2. 261, 27 4 2. 261, 27 1. 285, 46 203, 51 1. 081, 95 1. 179, 32 1. 285, 46 106, 14 1. 179, 32 Totals 6. 427, 30 1. 427, 31 5. 000, 00 60 0, 00