Topic 3 Derivatives Options puts and calls

Topic 3: Derivatives • Options: puts and calls • How much is an option worth? • [Forwards and futures] • [Swaps] • [Structured finance]

A call option Gives the holder the right* to purchase a security at the exercise price (a) on or before the expiry date (American option) (b) on the expiry date (European option) Generally American options are more valuable than European (why? ). But in the case of a non-dividend paying stock, an American option may be sold, but will never be exercised before the expiry date. *but no obligation

Other terms • A put option: …the right to sell a security… • Don’t forget: you can sell or buy an option • At the money: price of security=exercise price • In the money: price of security>exercise price • Out of the money: price of security

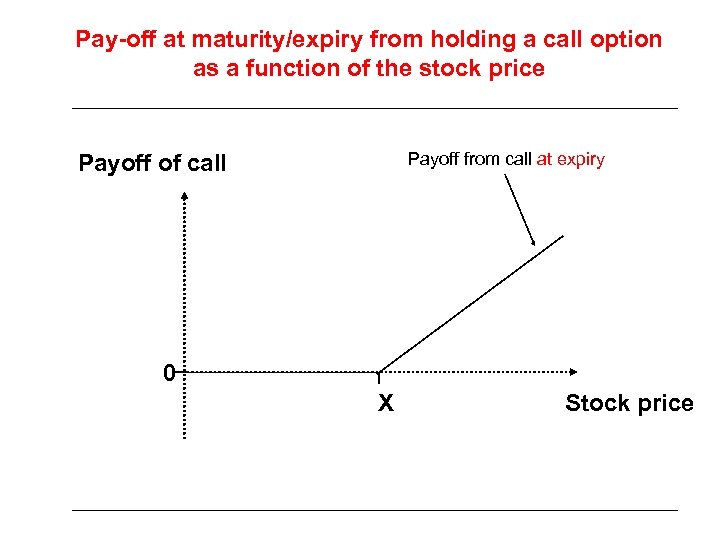Pay-off at maturity/expiry from holding a call option as a function of the stock price Payoff from call at expiry Payoff of call 0 X Stock price

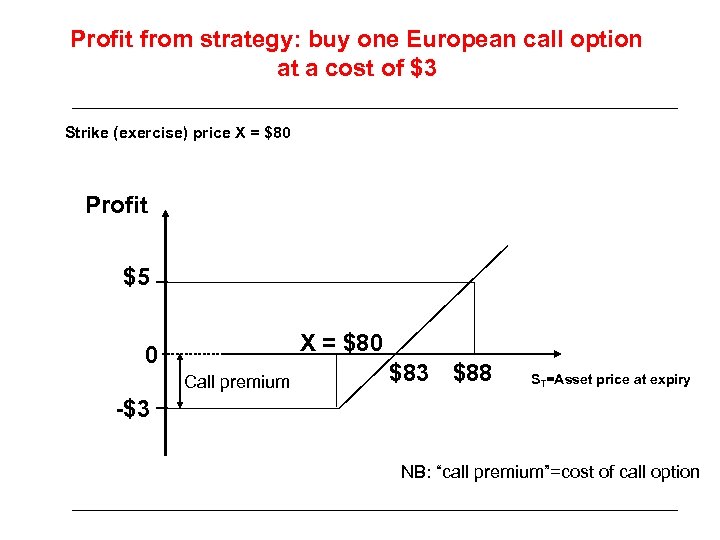Profit from strategy: buy one European call option at a cost of $3 Strike (exercise) price X = $80 Profit $5 X = $80 0 Call premium $83 $88 ST=Asset price at expiry -$3 NB: “call premium”=cost of call option

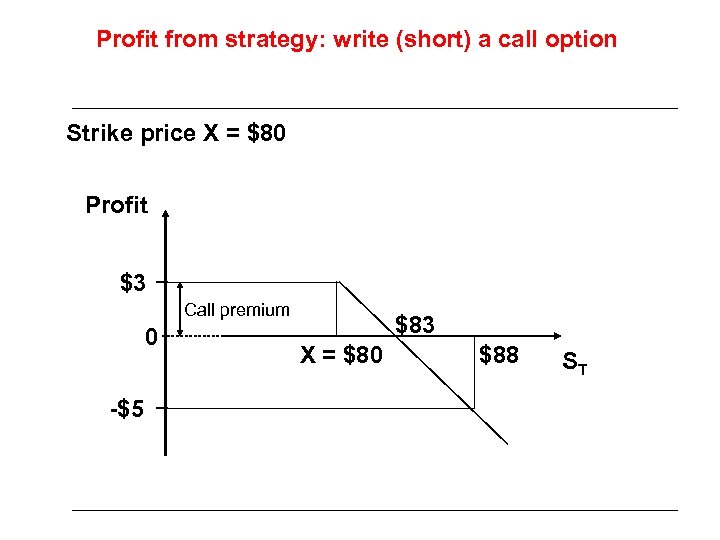Profit from strategy: write (short) a call option Strike price X = $80 Profit $3 Call premium 0 -$5 $83 X = $80 $88 ST

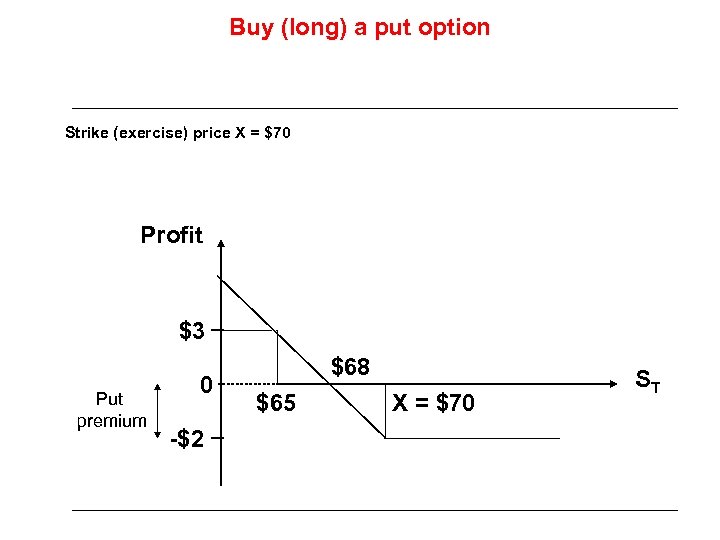Buy (long) a put option Strike (exercise) price X = $70 Profit $3 Put premium 0 -$2 $68 $65 X = $70 ST

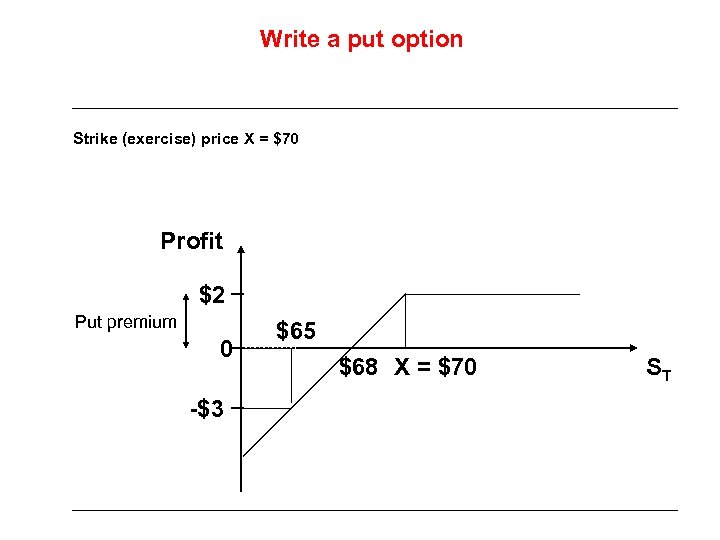Write a put option Strike (exercise) price X = $70 Profit $2 Put premium 0 -$3 $65 $68 X = $70 ST

Some live option prices http: //www. ise. com/Web. Form/m d_livevol. aspx? category. Id=12 4&header 3=true&menu 1=true International securities exchange >>Market trading and data tools >> Quotes, volatility and calculator

Why hold a call or put in your portfolio? Although often seen (and used) as risky, speculative instruments, options can be a valuable part of a risk management strategy e. g. : Protective put: – You’d like to invest in a stock, but want to limit your downside risk – Note that the same can be achieved by holding a call plus a bond Fraudster Madoff’s supposed plan: “split-strike”

In algebra If S is the market price of the security X the exercise price and T the expiry date. Payoff to call holder: ST – X if ST > X ; 0 otherwise Payoff to call writer: – (ST – X) if ST > X ; 0 otherwise

Put-call parity: • The value of a call must equal: • the value of the underlying stock plus • the value of a put with the same exercise price etc minus • A bond with the same maturity value as the exercise price of the stock

Why hold a call or put in your portfolio? (2) Solutions to views about risk patterns: Problem: You might think a security is headed for a period of volatility: but you don’t know if it will go up or down: Solution: Hold a “straddle”, i. e. a call and a put simultaneously (with the same exercise price and same maturity Problem: You think the security will go up but not all that much, so would like to benefit from the upside, but not pay the full call option premium Solution: Hold a spread, i. e. hold a call and write another call with a higher exercise price:

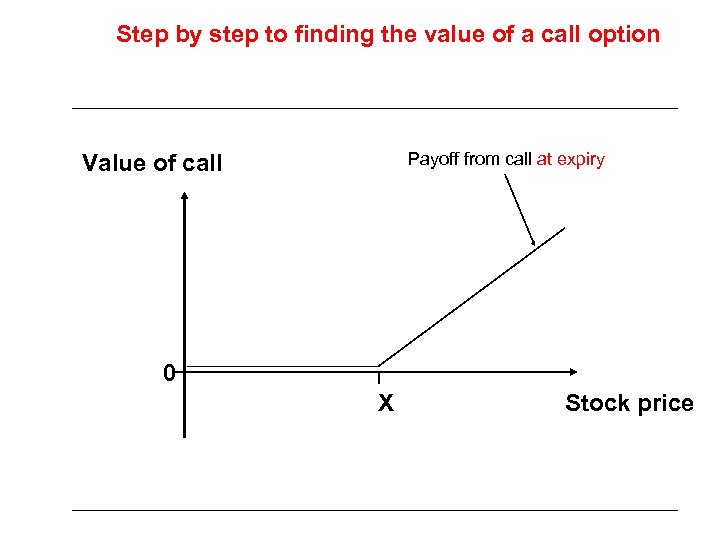Step by step to finding the value of a call option Payoff from call at expiry Value of call 0 X Stock price

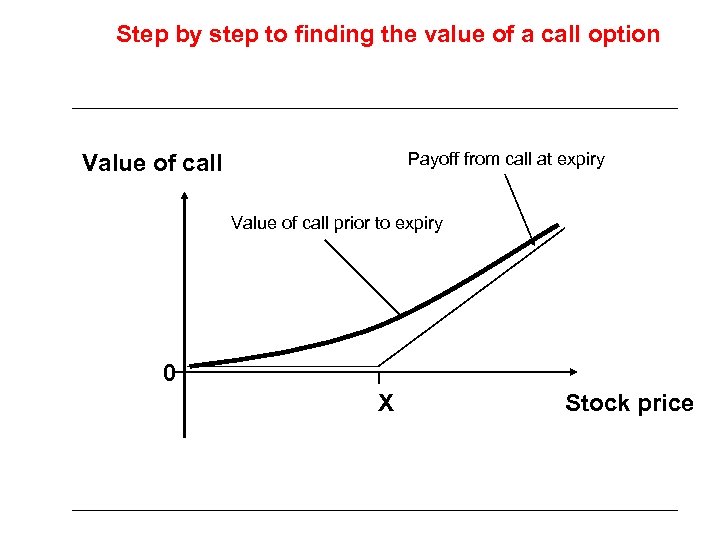Step by step to finding the value of a call option Payoff from call at expiry Value of call prior to expiry 0 X Stock price

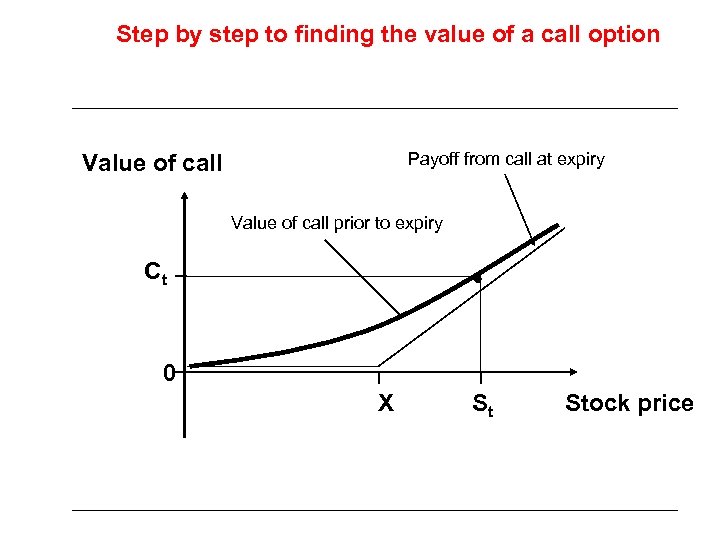Step by step to finding the value of a call option Payoff from call at expiry Value of call prior to expiry Ct 0 X St Stock price

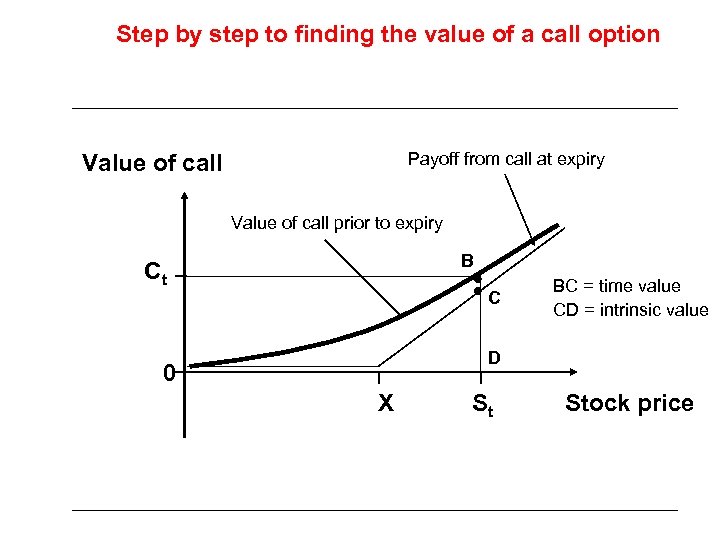Step by step to finding the value of a call option Payoff from call at expiry Value of call prior to expiry B Ct C BC = time value CD = intrinsic value D 0 X St Stock price

Options in unexpected places • An equity claim on a leveraged firm is an option • A collateralized loan is (for the lender) like a call on the collateral • An investment idea which can be implemented sometime in the future is like an option: when to exercise it?

How much should you pay for an option? • Simple case: two period, two states of world (u and d) • Find a portfolio that perfectly hedges the option • Payoffs equal in both states • One holds the stock (and some borrowing) • The other holds the option • This portfolio must have the same value as the stock

How much should you pay for an option? (2) • We find that the price does depend on the interest rate for borrowing • But not on the final stock price or the beta of the stock • Hedge ratio: how many units of the stock needed to hedge the option?

How much should you pay for an option? (3) • More general: two period, three states of world – could come from two half-steps (uu, ud, du and dd) • And we can continue the subdivision …. to continuous time …. and the binomial gets closer to a Normal distribution • The maths gets more complicated • (Stochastic calculus) • (Black and Scholes)

How much should you pay for an option? (4) N(d) = The probability that a random draw from a standard Normal (Gaussian) distribution will be less than d.

How much should you pay for an option? (4) Price of stock Price of call Interest rate Exercise price Time to maturity Stock price volatility N(d) = The probability that a random draw from a standard Normal (Gaussian) distribution will be less than d.

How much should you pay for an option? (5) Surprising feature of the Black-Scholes solution: Option value does not depend on the expected rate of return on the stock If N close to 1, then stock price is well above exercise price (relative to the volatility), so option almost certain to be exercised

How much should you pay for an option? (6) Surprising feature of the Black-Scholes solution: Option value does not depend on the expected rate of return on the stock The data needs: if we believe Black-Scholes and want to know option prices, hardest part is stock volatility σ Implied volatility: if we know the option price and believe Black-Scholes, then we can solve back for σ If N close to 1, then stock price is well above exercise price (relative to the volatility), so option almost certain to be exercised

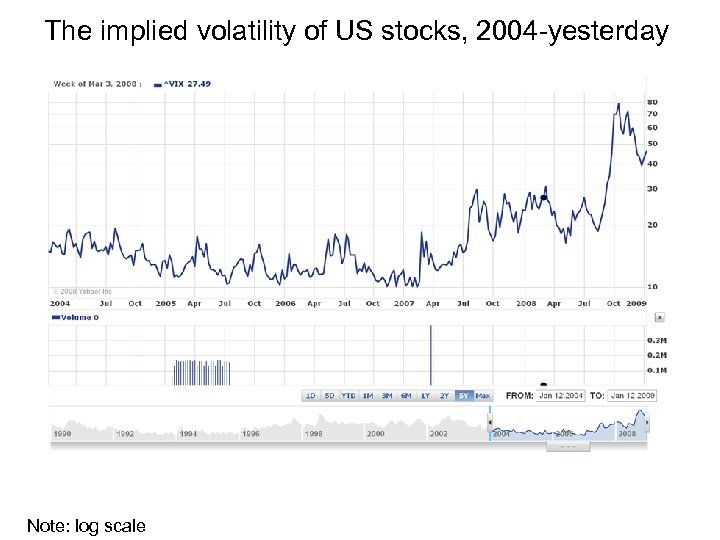The implied volatility of US stocks, 2004 -yesterday Note: log scale

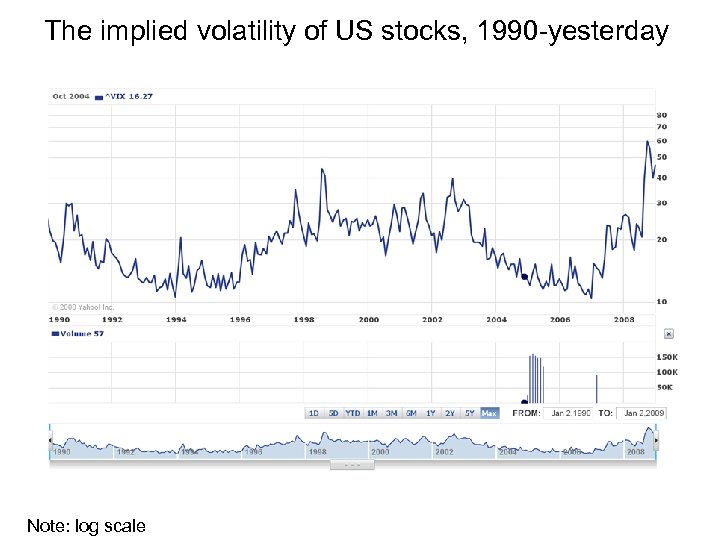The implied volatility of US stocks, 1990 -yesterday Note: log scale

Hedge ratio (“delta”) • (Already defined for the two-state model) • Is the change in the price of the option for a $1 increase in the stock price – i. e. the slope of the option price curve • Is less than one (for call option) – But note that elasticity of option price with respect to stock price is higher – Equals N(d 1) in the Black Scholes formula • Think of it as the defining the proportions in which options and stocks must be held to hedge the risk

Assumptions underlying Black. Scholes and how well does it fit? • “Brownian motion” – normally distributed continuous price changes – no jumps • Fits quite well • But, especially after 1987, implied volatility seems systematically related to exercise price • Deep in the money puts are expensive • The volatility “smirk”

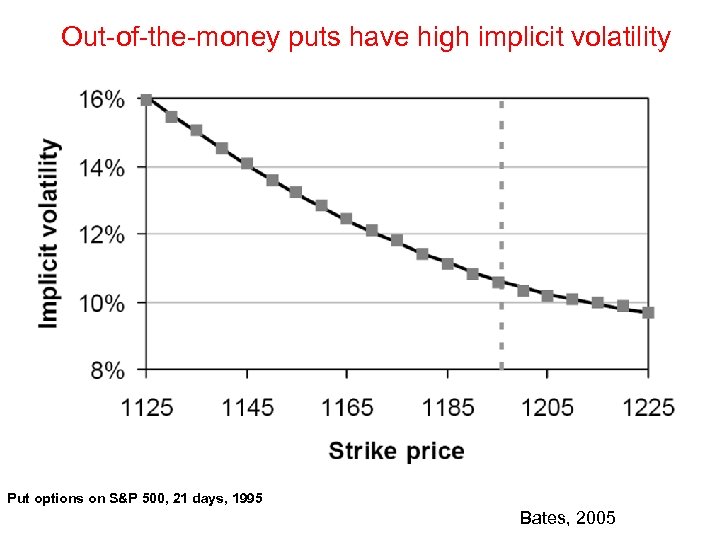Out-of-the-money puts have high implicit volatility Put options on S&P 500, 21 days, 1995 Bates, 2005

The Smirk

Out-of-the-money puts have high implicit volatility The Smirk Put options on S&P 500, 21 days, 1995 Bates, 2005

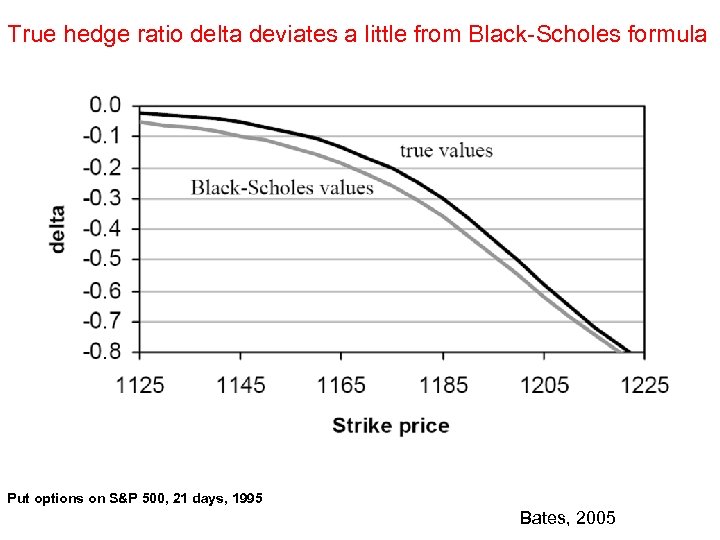True hedge ratio delta deviates a little from Black-Scholes formula Put options on S&P 500, 21 days, 1995 Bates, 2005

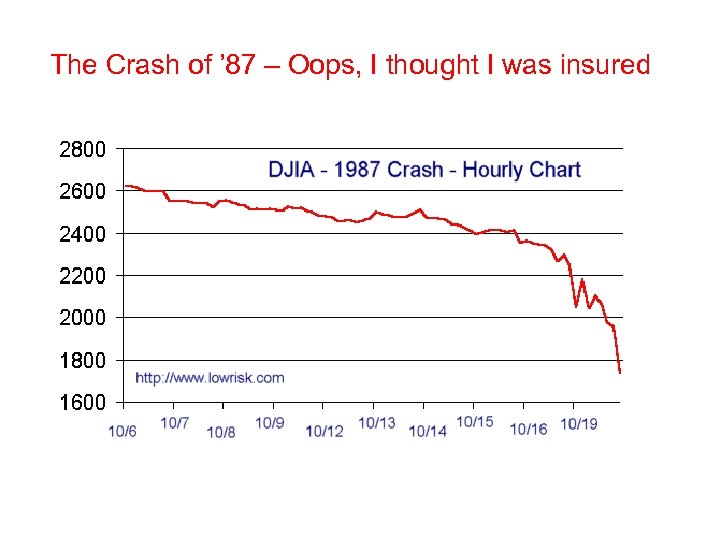The Crash of ’ 87 – Oops, I thought I was insured

The Crash of ’ 87 – Oops, I thought I was insured

Dynamic hedging and the crash of October 19, 1987 • Portfolio insurance products used dynamic hedging to try to eliminate downside risk – (using “protective” puts) • But market movements were too sudden – dynamic hedging adjustments couldn’t keep up with price movements – deltas increased and insurers needed to buy more puts and/or sell stock – Information systems couldn’t keep up – price information was out of date – Trading stopped for a while in some stocks and derivatives • So the insurance did not work properly – And indeed helped to destabilize the market – One-day fall in US stock prices of 20%

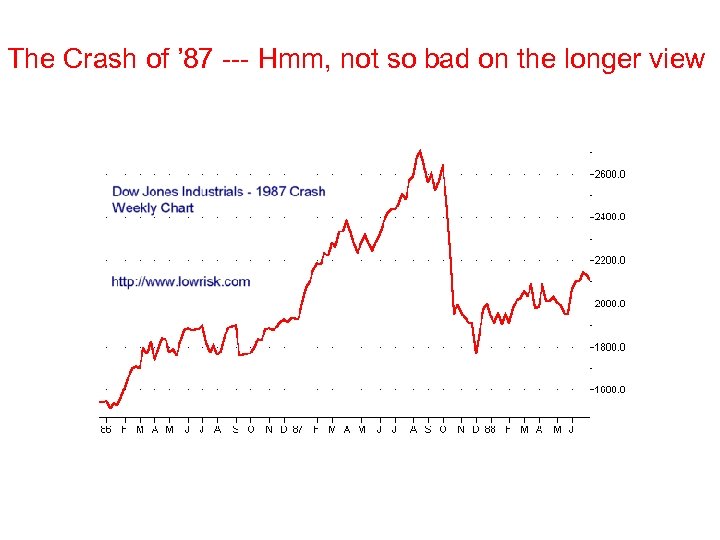The Crash of ’ 87 --- Hmm, not so bad on the longer view

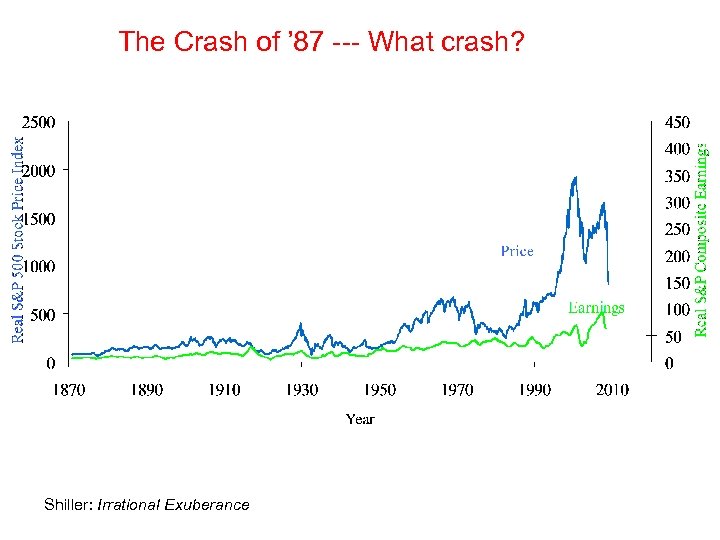The Crash of ’ 87 --- What crash? Shiller: Irrational Exuberance

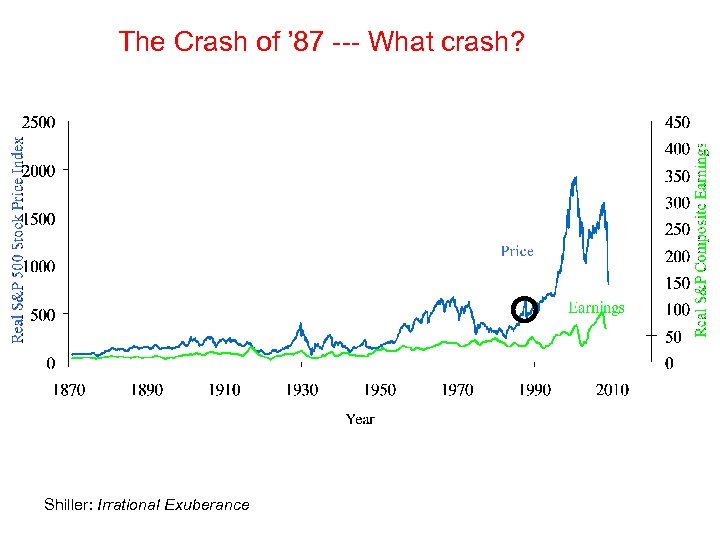The Crash of ’ 87 --- What crash? Shiller: Irrational Exuberance

Forward and futures markets • Forwards useful for hedging a known commitment due in the future. • Forward transactions and futures markets do much the same thing • Forward transactions are bilaterally negotiated or offered “over-thecounter” by e. g. a bank • Futures markets are organized exchanges where standardized contracts are traded…and the final settlement is in cash for the difference between spot and forward