dbd8324489ac696a02c4505661ddb028.ppt
- Количество слайдов: 104

Topic 28 Flexible Assembly Systems Spring 2002 IE 514 1

Job Shops z Each job has an unique identity z Make to order, low volume environment z Possibly complicated route through system z Very difficult Spring 2002 Flexible Assembly z Limited number of product types z Given quantity of each type z Mass production z High degree of automation z Even more difficult! IE 514 2

Flexible Assembly Systems Sequencing Unpaced Assembly Systems Simple flow line with finite buffers Application: assembly of copiers Sequencing Paced Assembly Systems Conveyor belt moves at a fixed speed Application: automobile assembly Scheduling Flexible Flow Systems Flow lines with finite buffers and bypass Application: producing printed circuit board Spring 2002 IE 514 3

Sequencing Unpaced Assembly Systems z. Number of machines in series z. No buffers z. Material handling system y. When a job finishes moves to next station y. No bypassing y. Blocking z. Can model any finite buffer situation Spring 2002 IE 514 4

Cyclic Schedules z. Schedules often cyclic or periodic: y. Given set of jobs scheduled in certain order x. Contains all product types x. May contain multiple jobs of same type y. Second identical set scheduled, etc. z. Practical if insignificant setup time y. Low inventory cost y. Easy to implement Spring 2002 IE 514 5

Minimum Part Set z Suppose l product types z Let Nk be target number of jobs of type k z Let z be the greatest common divisor z Then is the smallest set with ‘correct’ proportions z Called the minimum part set (MPS) Spring 2002 IE 514 6

Defining a Cyclic Schedule z. Consider the jobs in the MPS as n jobs z. Let pij be as before z. A cyclic schedule is determined by sequencing the job in the MPS z. Maximizing TP = Minimizing cycle time Spring 2002 IE 514 7
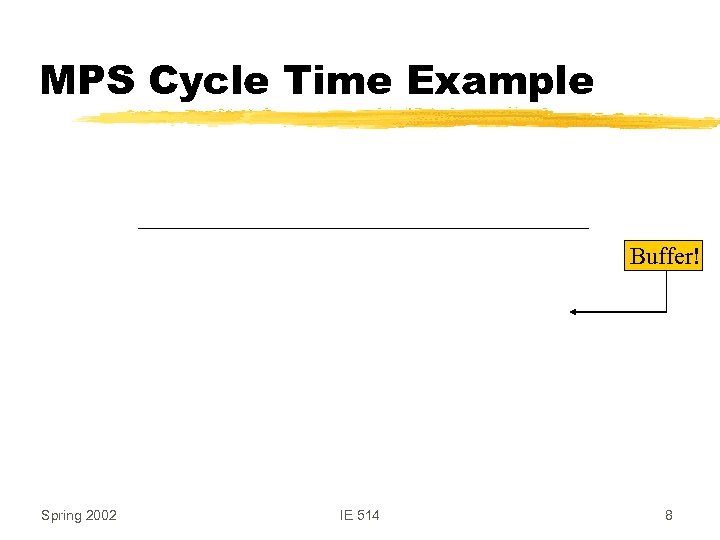
MPS Cycle Time Example Buffer! Spring 2002 IE 514 8
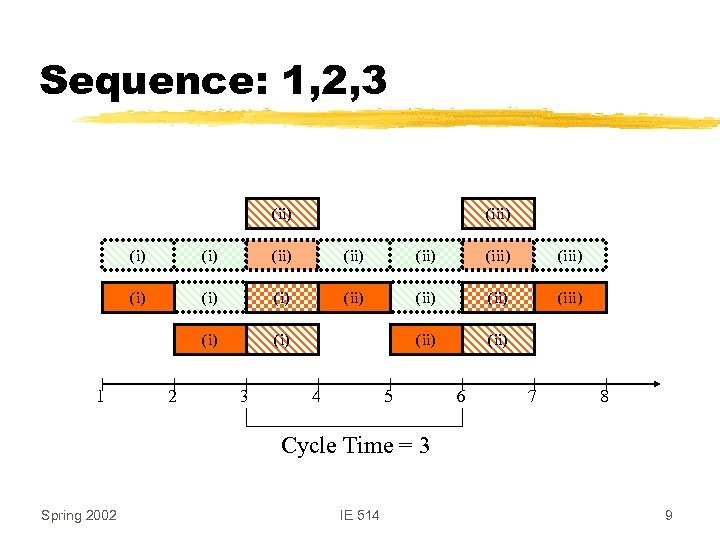
Sequence: 1, 2, 3 (ii) (i) (ii) (iii) (i) (ii) (i) 1 (i) (ii) 2 3 4 5 6 7 8 Cycle Time = 3 Spring 2002 IE 514 9
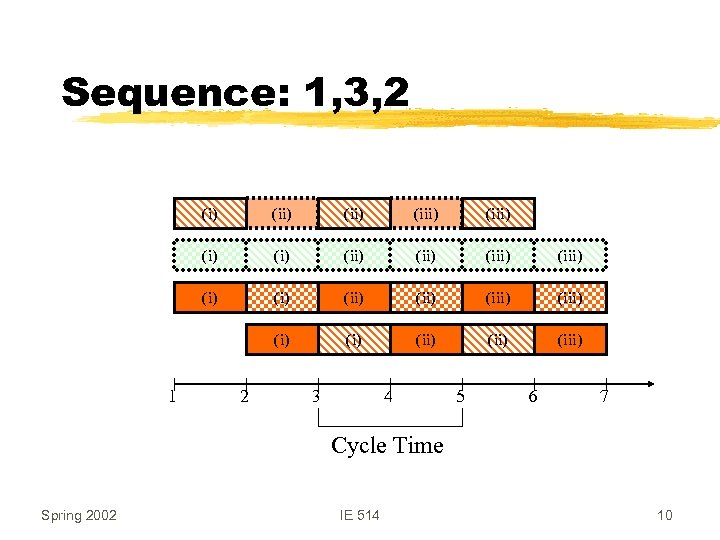
Sequence: 1, 3, 2 (i) (ii) (iii) (i) (i) (ii) (iii) (i) 1 (ii) (iii) 2 3 4 5 6 7 Cycle Time Spring 2002 IE 514 10

Minimizing Cycle Time z. Profile Fitting (PF) heuristic: y. Select first job j 1 x. Arbitrarily x. Largest amount of processing y. Generates profile y. Determine which job goes next Spring 2002 IE 514 11

PF: Next Job z. Compute for each candidate job y. Time machines are idle y. Time job is blocked y. Start with departure times: Spring 2002 IE 514 12

Nonproductive Time z. Calculate sum of idle and blocked time z. Repeat for all remaining jobs in the MPS z. Select job with smallest number z. Calculate new profile and repeat Spring 2002 IE 514 13

Discussion: PF Heuristic z. PF heuristic performs well in practice z. Refinement: y. Nonproductive time is not equally bad on all machines y. Bottleneck machine y. Use weight in the sum Spring 2002 IE 514 14

Discussion: PF Heuristic z. Basic assumptions y. Setup is not important y. Low WIP is important Cyclic schedules good z. Want to maximize throughput Minimize cycle time PF heuristic performs well Spring 2002 IE 514 15

Discussion: FMS z Flexible Manufacturing Systems (FMS) y. Numerically Controlled machines y. Automated Material Handling system y. Produces a variety of product/part types z Scheduling y. Routing of jobs y. Sequencing on machines y. Setup of tools z Similar features but more complicated Spring 2002 IE 514 16

Discussion: Solution Methods z. Formulated as ‘simple’ sequencing z. Can apply branch-and-bound z. In general constraints make mathematical programming formulation difficult z. PF heuristic easy to generalize Spring 2002 IE 514 17

Additional Complications z. The material handling system does not wait for a job to complete Paced assembly systems z. There may be multiple machines at each station and/or there may be bypass Flexible flow systems with bypass Spring 2002 IE 514 18

Topic 29 Paced Assembly Systems Spring 2002 IE 514 19

Paced Assembly Systems z. Conveyor moves jobs at fixed speeds z. Fixed distance between jobs y. Spacing proportional to processing time z. No bypass z. Unit cycle time ytime between two successive jobs Spring 2002 IE 514 20

Grouping and Spacing z. Attributes and characteristics of each job ycolor, options, destination of cars z. Changeover cost y. Group operations with high changeover z. Certain long operations y. Space evenly over the sequence y. Capacity constrained operations (criticality index) Spring 2002 IE 514 21

Objectives z. Minimize total setup cost z. Meet due dates for make-to-order jobs y. Total weighted tardiness z. Spacing of capacity constrained operations y. Pi(l) = penalty for working on two jobs l positions apart in ith workstation z. Regular rate of material consumption Spring 2002 IE 514 22

Grouping and Spacing Heuristic z. Determine the total number of jobs to be scheduled z. Group jobs with high setup cost operations z. Order each subgroup accounting for shipping dates z. Space jobs within subgroups accounting for capacity constrained operations Spring 2002 IE 514 23

Example z. Single machine with 10 jobs z. Each job has a unit processing time z. Setup cost z. If Spring 2002 there is a penalty cost IE 514 24

Example Data Spring 2002 IE 514 25

Grouping z. Group A: Jobs 1, 2, and 3 z. Group B: Jobs 4, 5, and 6 z. Group C: Jobs 7, 8, 9, and 19 z. Best order: A B C Spring 2002 IE 514 26
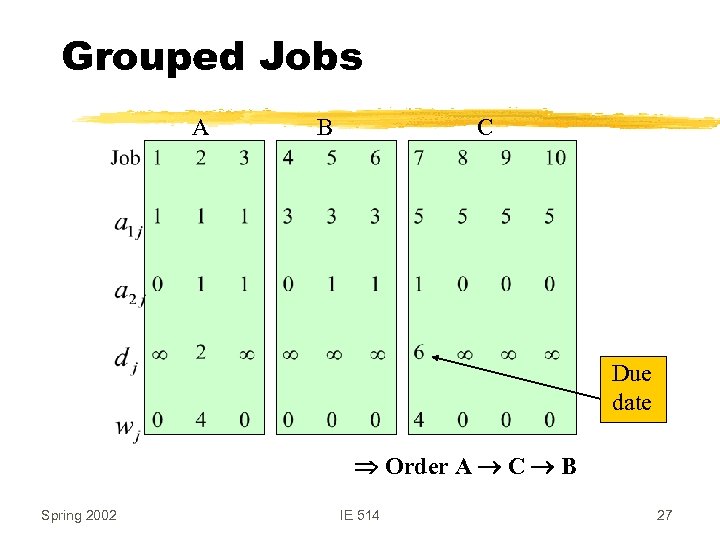
Grouped Jobs A B C Due date Order A C B Spring 2002 IE 514 27
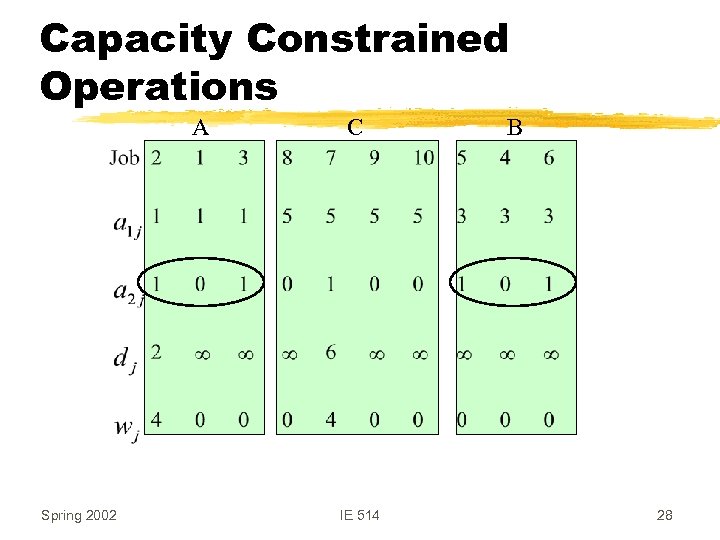
Capacity Constrained Operations A Spring 2002 C IE 514 B 28

Topic 30 Flexible Flow Systems Spring 2002 IE 514 29
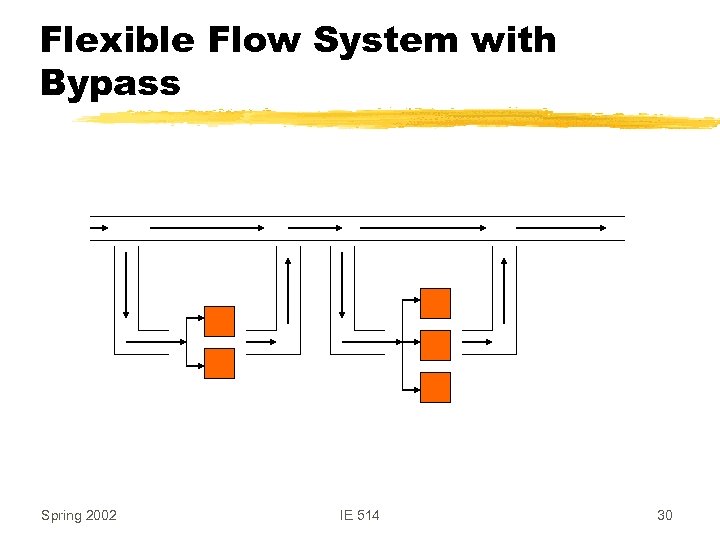
Flexible Flow System with Bypass Spring 2002 IE 514 30
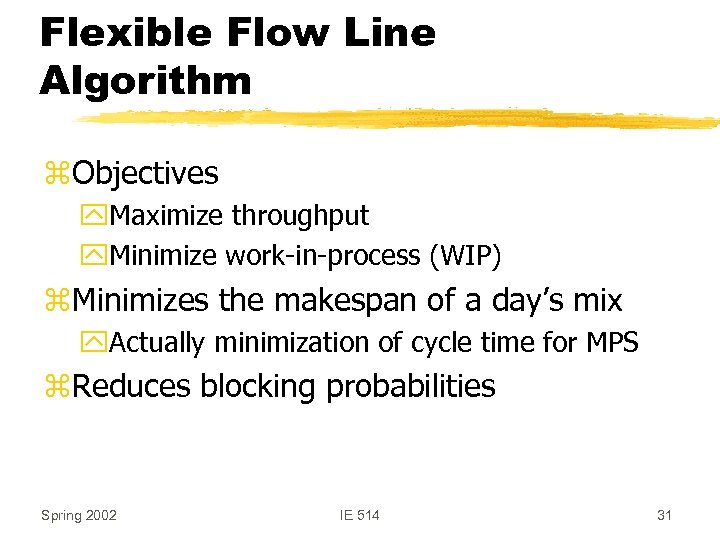
Flexible Flow Line Algorithm z. Objectives y. Maximize throughput y. Minimize work-in-process (WIP) z. Minimizes the makespan of a day’s mix y. Actually minimization of cycle time for MPS z. Reduces blocking probabilities Spring 2002 IE 514 31
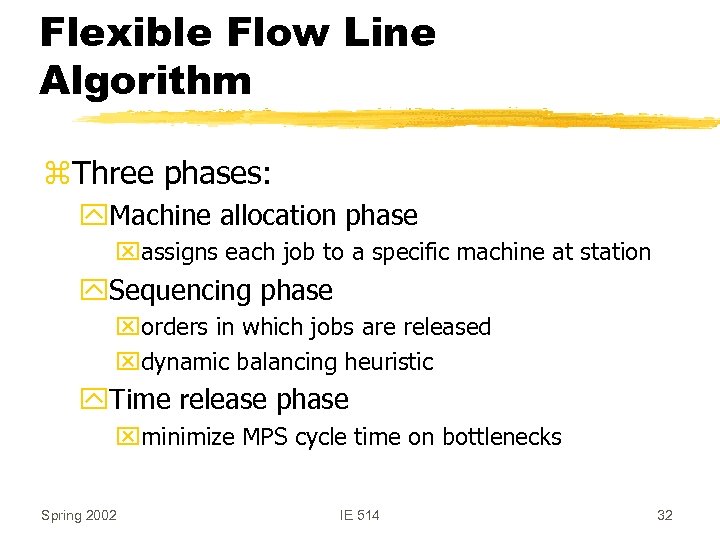
Flexible Flow Line Algorithm z. Three phases: y. Machine allocation phase xassigns each job to a specific machine at station y. Sequencing phase xorders in which jobs are released xdynamic balancing heuristic y. Time release phase xminimize MPS cycle time on bottlenecks Spring 2002 IE 514 32

Machine Allocation z. Bank of machines z. Which machine for which job? z. Basic idea: workload balancing z. Use LPT dispatching rule Spring 2002 IE 514 33

Sequencing z. Basic idea: spread out jobs sent to the same machine z. Dynamic balancing heuristic z. For a given station, let pij be processing time of job j on ith machine z. Let Spring 2002 IE 514 34

Dynamic Balancing Heuristic z. Let Sj be the jobs released before and including job j z. Define z. Target Spring 2002 IE 514 35

Minimizing Overload z. Define the overload of the ith machine z. The cumulative overload is z. Minimize Spring 2002 IE 514 36

Release Timing z. MPS workload of each machine known y. Highest workload = bottleneck y. MPS cycle time Bottleneck cycle time z. Algorithm y. Step 1: Release all jobs as soon as possible y. Step 2: Delay all jobs upstream from bottleneck as much as possible y. Step 3: Move up all jobs downstream from the bottleneck as much as possible Spring 2002 IE 514 37
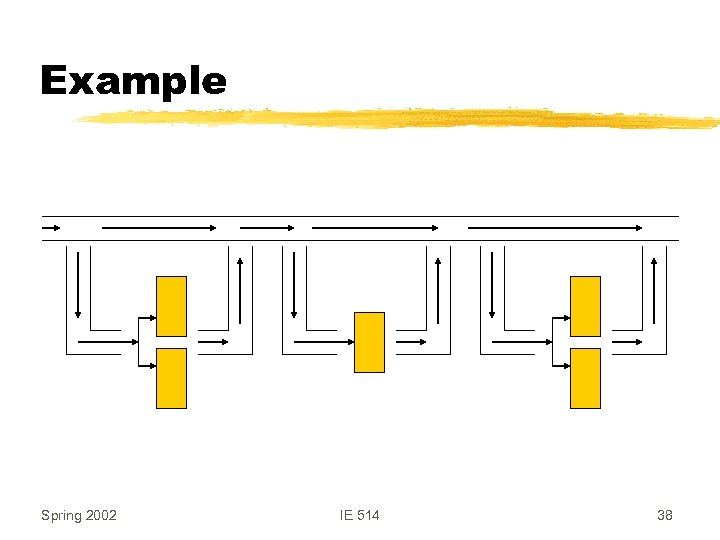
Example Spring 2002 IE 514 38

Data Spring 2002 IE 514 39

Machine Allocation Spring 2002 IE 514 40
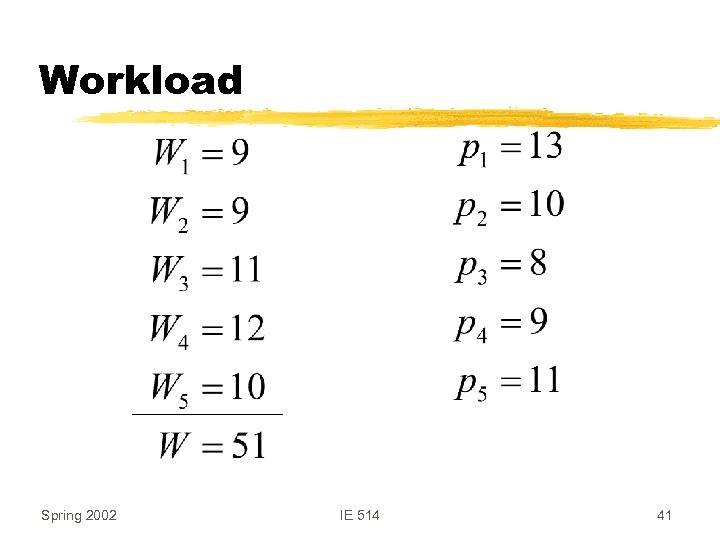
Workload Spring 2002 IE 514 41

Overload Spring 2002 IE 514 42
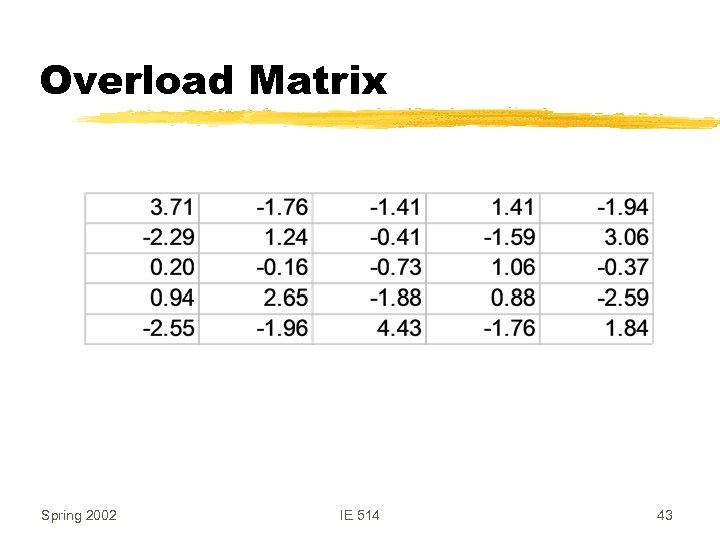
Overload Matrix Spring 2002 IE 514 43
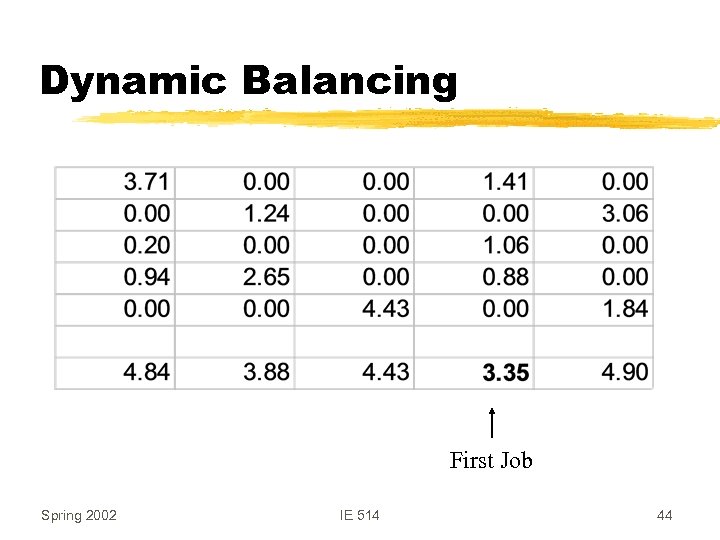
Dynamic Balancing First Job Spring 2002 IE 514 44

Selecting the Second Job z. Calculate the cumulative overload where Spring 2002 IE 514 45

Cumulative Overload Selected next Spring 2002 IE 514 46

Final Cycle z. Schedule jobs 4, 5, 1, 3, 2 z. Release timing phase y. Machine 4 is the bottleneck y. Delay jobs on Machine 1, 2, and 3 y. Expedite jobs on Machine 5 Spring 2002 IE 514 47

Topic 31 Lot Sizing Spring 2002 IE 514 48

Lot Sizing z. Domain: ylarge number of identical jobs ysetup time/cost significant ysetup may be sequence dependent z. Terminology yjobs = items ysequence of identical jobs = run Spring 2002 IE 514 49

Applications z. Continuous manufacturing ychemical, paper, pharmaceutical, etc. z. Service industry yretail procurement Spring 2002 IE 514 50

Objective z. Minimize total cost ysetup cost yinventory holding cost z. Trade-off z. Cyclic schedules Spring 2002 IE 514 51

Scheduling Decisions z. Determine the length of runs ylot sizes z. Determine the order of the runs ysequence to minimize setup cost z. Economic Lot Scheduling Problem (ELSP) Spring 2002 IE 514 52

Overview z. One type of item/one machine z. Several types of items/one machine yrotation schedules yarbitrary schedules z. Generalizations to multiple machines Spring 2002 IE 514 53

Problem Description z. Single machine z. Single item type z. Production rate q/time z. Demand rate g/time z. Problem: determine the run length Spring 2002 IE 514 54
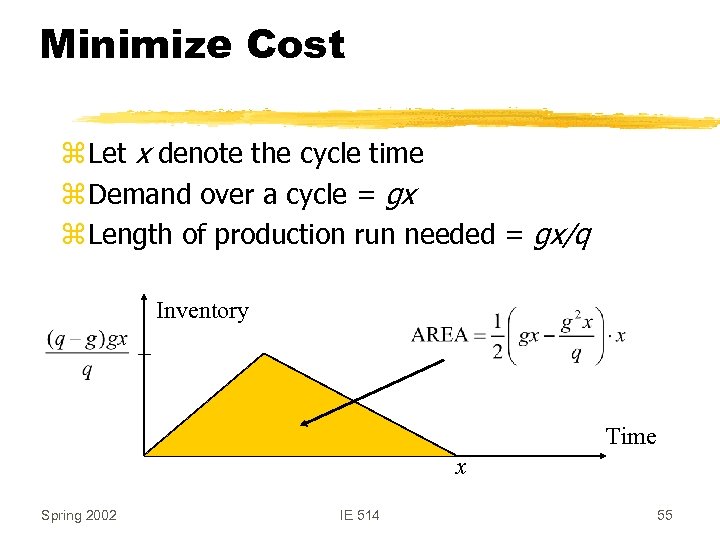
Minimize Cost z Let x denote the cycle time z Demand over a cycle = gx z Length of production run needed = gx/q Inventory Time x Spring 2002 IE 514 55
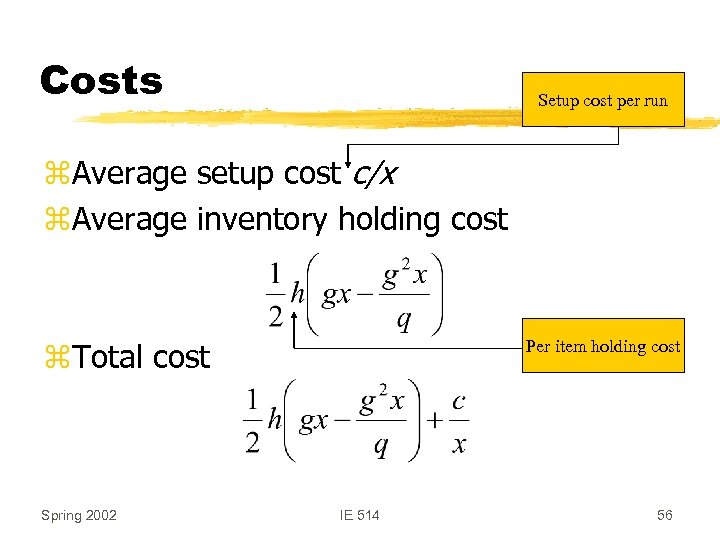
Costs Setup cost per run z. Average setup cost c/x z. Average inventory holding cost Per item holding cost z. Total cost Spring 2002 IE 514 56

Optimizing Cost z. Derivative z. Solve Spring 2002 IE 514 57
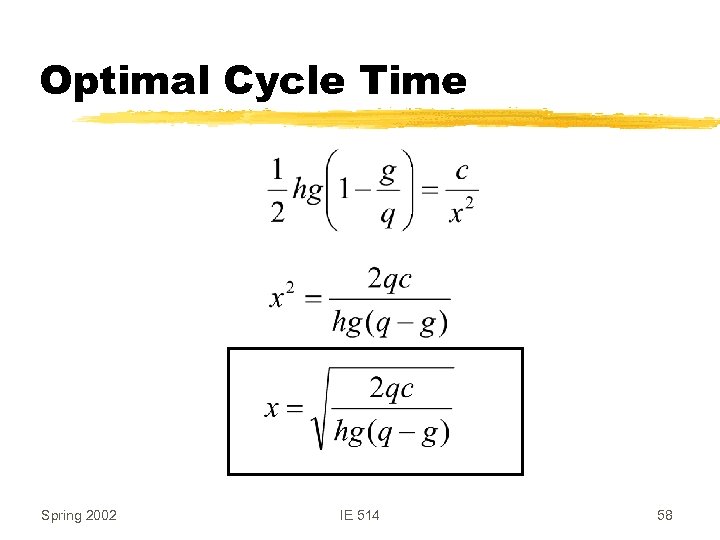
Optimal Cycle Time Spring 2002 IE 514 58
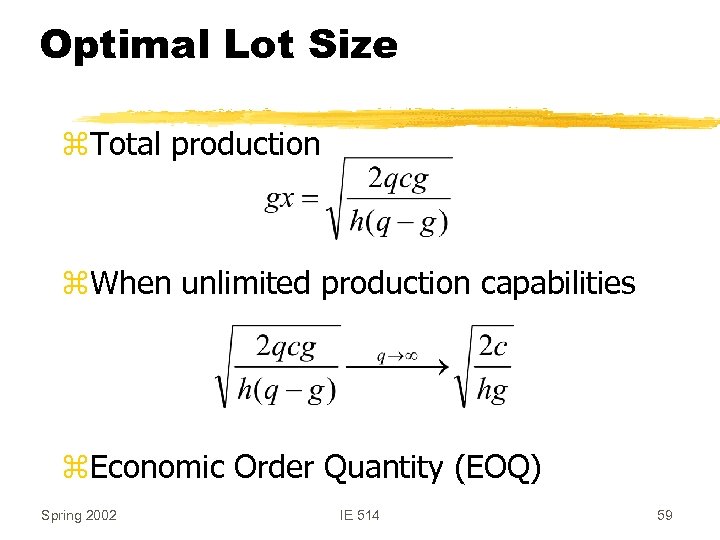
Optimal Lot Size z. Total production z. When unlimited production capabilities z. Economic Order Quantity (EOQ) Spring 2002 IE 514 59
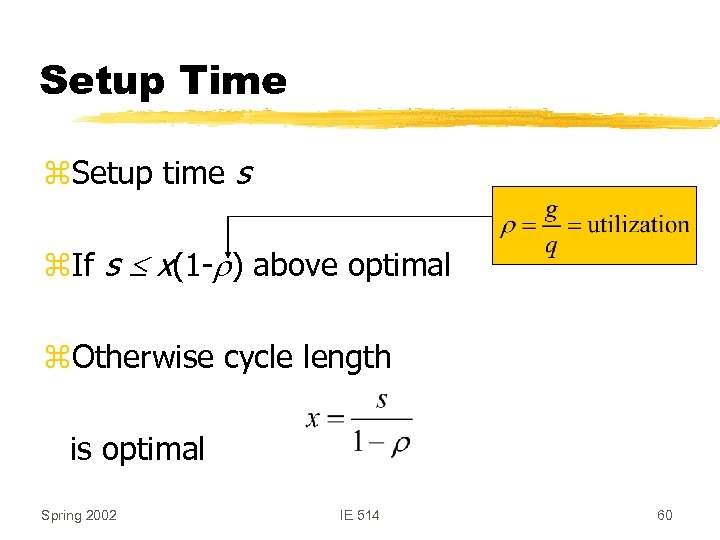
Setup Time z. Setup time s z. If s x(1 -r) above optimal z. Otherwise cycle length is optimal Spring 2002 IE 514 60

Numerical Example z. Production z. Demand z. Setup cost z. Holding cost Spring 2002 q = 90/month g = 50/month c = $2000 h = $20/item IE 514 61

Optimal Schedule z. Cycle time = 3 months z. Lot size = 150 items z. Idle time = 3(1 -5/9)=1. 33 months Spring 2002 IE 514 62

Example: Setup Times z. Now assume setup time z. If < 1. 33 months then 3 month cycle still optimal z. Otherwise the cycle time must be longer Spring 2002 IE 514 63
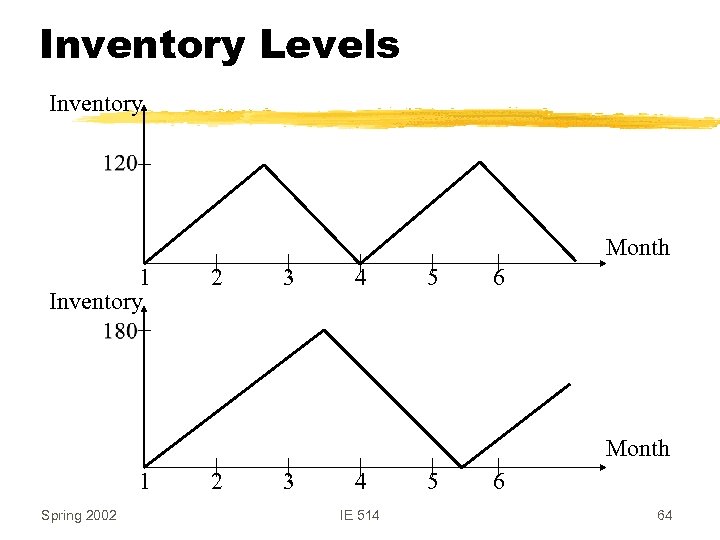
Inventory Levels Inventory Month 1 Inventory 2 3 4 5 6 Month 1 Spring 2002 2 3 4 IE 514 5 6 64

Example z A plant needs to produce 10000 car chassis per year z The plant capacity is 25000 chassis/year z Each chassis costs $2000 z It costs $200 to set up a production run z Holding cost is $500/chassis/year z What is the optimal lot size? Spring 2002 IE 514 65

Solution z. The optimal lot size is which means we should make runs in a year. Spring 2002 IE 514 66

Discussion z. Notice that the preceding result does not tell us how to produce those chassis in detail z. Lot size models are used for planning z. Time horizon usually a few months (short range planning) Spring 2002 IE 514 67

Topic 33 Lot Sizing with Multiple Items Spring 2002 IE 514 68

Multiple Items z Only considered one item type before z Now assume n different items z Demand rate for item j is gj z Production rate of item j is qj z Setup independent of the sequence z Rotation schedule: single run of each item Spring 2002 IE 514 69

Scheduling Decision z. Cycle length determines the run length for each item z. Only need to determine the cycle length x z. Expression for total cost/time unit Spring 2002 IE 514 70

Inventory Holding Cost z. Average inventory level for the j-th item z. Average total cost Spring 2002 IE 514 71

Optimal Lot-Size z. Solve as before z. Limiting case (infinite production rate) Spring 2002 IE 514 72

Example Spring 2002 IE 514 73
Solution Spring 2002 IE 514 74

Solution z. The total average cost per time unit is z. How can we do better than this? Spring 2002 IE 514 75

Topic 34 Lot Sizing with Setup Spring 2002 IE 514 76

Setup Times z. With sequence independent setup costs and no setup times the sequence within each lot does not matter Only a lot sizing problem z. Even with setup times, if they are not job dependent then still only lot sizing Spring 2002 IE 514 77

Job Independent Setup Times z. If sum of setup times < idle time then our optimal cycle length remains optimal z. Otherwise we take it as small as possible Spring 2002 IE 514 78

Job Dependent Setup Times z. Now there is a sequencing problem z. Objective: minimize sum of setup times z. Equivalent to the Traveling Salesman Problem (TSP) y. A salesman must visit n cities exactly once with the objective of minimizing the total travel time, starting and ending in the same city Spring 2002 IE 514 79

Equivalence to TSP z Item = city z Travel time = setup time z TSP is NP-hard z If best sequence has sum of setup times < idle time optimal lot size and sequence Spring 2002 IE 514 80

Long setup z. If sum of setups > idle time, then the optimal schedule has the property: y. Each machine is either producing or being setup for production z. An extremely difficult problem with arbitrary setup times Spring 2002 IE 514 81

Arbitrary Schedules z Sometimes a rotation schedule does not make sense (remember problem with no setup cost) z For example, we might want to allow a cycle 1, 4, 2, 4, 3, 4 if item 4 has no setup cost z No efficient algorithm exists Spring 2002 IE 514 82

Problem Formulation z. Assume sequence-independent setup z. Formulate as a nonlinear program Spring 2002 IE 514 83

Notation z. Setup cost and setup times z. All possible sequences z. Item k produces in l-th position z. Setup time sl, run time tl, and idle time ul Spring 2002 IE 514 84

Inventory Cost z. Let x be the cycle time z. Let v be the time between production of k z. Total inventory cost for k is Spring 2002 IE 514 85

Mathematical Program Subject to Spring 2002 IE 514 86

Two Problems z. Master problem yfinds the best sequence z. Subproblem yfinds the best production times, idle times, and cycle length z. Key idea: think of them seperately Spring 2002 IE 514 87

Subproblem Subject to Spring 2002 IE 514 88

Master Problem z. Sequencing complicated z. Heuristic approach z. Frequency Fixing and Sequencing (FFS) z. Focus on how often to produce each item y. Computing relative frequencies y. Adjusting relative frequencies y. Sequencing Spring 2002 IE 514 89

Computing Relative Frequencies z. Let yk denote the number of times item k is produced in a cycle z. We will ysimplify the objective function by substituting ydrop the second constraint Spring 2002 IE 514 90

Mathematical Program Subject to Spring 2002 IE 514 91
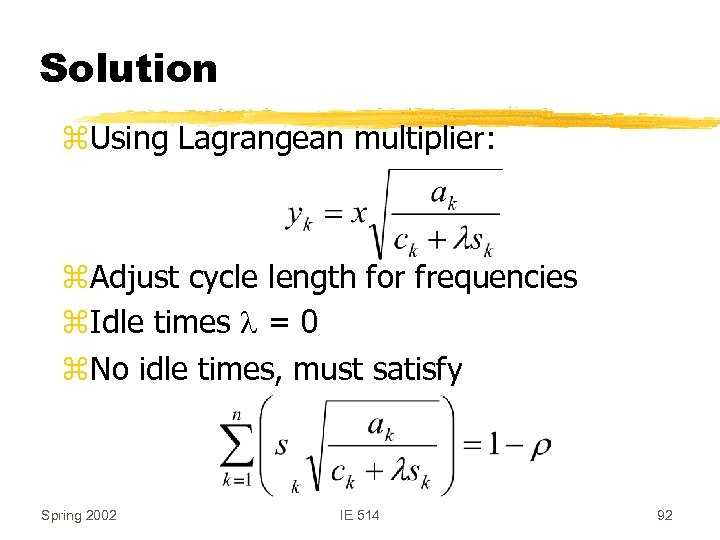
Solution z. Using Lagrangean multiplier: z. Adjust cycle length for frequencies z. Idle times l = 0 z. No idle times, must satisfy Spring 2002 IE 514 92

Adjusting the Frequencies z. Adjust the frequencies such that they are yinteger ypowers of 2 ycost within 6% of optimal cost z. New frequencies and run times Spring 2002 IE 514 93

Sequencing z. Variation of LPT z. Calculate z. Consider the problem with machines in parallel and jobs of length z. List pairs in decreasing order z. Schedule one at a time considering spacing Spring 2002 IE 514 94

Topic 35 Lot Sizing on Multiple Machines Spring 2002 IE 514 95

Multiple Machines z. So far, all models single machine models z. Extensions to multiple machines yparallel machines yflow shop yflexible flow shop Spring 2002 IE 514 96

Parallel Machines z. Have m identical machines in parallel z. Setup cost only z. Item process on only one machine z. Assume yrotation schedule yequal cycle for all machines Spring 2002 IE 514 97

Decision Variables z. Same as previous multi-item problem z. Addition: assignment of items to machines z. Objective: balance the load z. Heuristic: LPT with Spring 2002 IE 514 98

Different Cycle Lengths z Allow different cycle lengths for machines z Intuition: should be able to reduce cost z Objective: assign items to machines to balance the load z Complication: should not assign items that favor short cycle to the same machine as items that favor long cycle Spring 2002 IE 514 99

Heuristic Balancing z. Compute cycle length for each item z. Rank in decreasing order z. Allocation jobs sequentially to the machines until capacity of each machine is reached z. Adjust balance Spring 2002 IE 514 100

Further Generalizations z. Sequence dependent setup z. Must consider ypreferred cycle time ymachine balance ysetup times z. Unsolved z. General schedules even harder! z. Research needed : -) Spring 2002 IE 514 101

Flow Shop z. Machines configured in series z. Assume no setup time z. Assume production rate of each item is identical for every machine Can be synchronized z. Reduces to single machine problem Spring 2002 IE 514 102

Variable Production Rates z. Production rate for each item not equal for every machine z. Difficult problem z. Little research z. Flexible flow shop: need even more stringent conditions Spring 2002 IE 514 103
Discussion z. Applicability of lot sizing models yshort range planning ydemand assumed known xdetermines throughput ymake-to-stock systems xdue date of little importance/not available xextensions to mixed systems z. Multiple facilities in series ysupply chain management Spring 2002 IE 514 104
dbd8324489ac696a02c4505661ddb028.ppt