3620d0e9a9f319615f401ee80dd17507.ppt
- Количество слайдов: 102
 Top Ten #1 Descriptive Statistics NOTE! This Power Point file is not an introduction, but rather a checklist of topics to review
Top Ten #1 Descriptive Statistics NOTE! This Power Point file is not an introduction, but rather a checklist of topics to review
 Location: central tendency • Population Mean =µ= Σx/N = (5+1+6)/3 = 12/3 = 4 • Algebra: Σx = N*µ = 3*4 =12 • Do NOT use if N is small and extreme values • Ex: Do NOT use if 3 houses sold this week, and one was a mansion
Location: central tendency • Population Mean =µ= Σx/N = (5+1+6)/3 = 12/3 = 4 • Algebra: Σx = N*µ = 3*4 =12 • Do NOT use if N is small and extreme values • Ex: Do NOT use if 3 houses sold this week, and one was a mansion
 Location • • • Median = middle value Ex: 5, 1, 6 Step 1: Sort data: 1, 5, 6 Step 2: Middle value = 5 OK even if extreme values Home sales: 100 K, 200 K, 900 K, so mean =400 K, but median = 200 K
Location • • • Median = middle value Ex: 5, 1, 6 Step 1: Sort data: 1, 5, 6 Step 2: Middle value = 5 OK even if extreme values Home sales: 100 K, 200 K, 900 K, so mean =400 K, but median = 200 K
 Location • • Mode: most frequent value Ex: female, female Mode = female Ex: 1, 1, 2, 3, 5, 8: mode = 1
Location • • Mode: most frequent value Ex: female, female Mode = female Ex: 1, 1, 2, 3, 5, 8: mode = 1
 Relationship • Case 1: if symmetric (ex bell, normal), then mean = median = mode • Case 2: if positively skewed to right, then mode
Relationship • Case 1: if symmetric (ex bell, normal), then mean = median = mode • Case 2: if positively skewed to right, then mode
 Dispersion • • • How much spread of data How much uncertainty Range = Max-Min > 0 But range affected by unusual values Ex: Santa Monica = 105 degrees once a century, but range would be 105 -min
Dispersion • • • How much spread of data How much uncertainty Range = Max-Min > 0 But range affected by unusual values Ex: Santa Monica = 105 degrees once a century, but range would be 105 -min
 Standard Deviation • Better than range because all data used • Population SD = Square root of variance =sigma =σ • SD > 0
Standard Deviation • Better than range because all data used • Population SD = Square root of variance =sigma =σ • SD > 0
 Empirical Rule • • • Applies to mound or bell-shaped curves Ex: normal distribution 68% of data within + one SD of mean 95% of data within + two SD of mean 99. 7% of data within + three SD of mean
Empirical Rule • • • Applies to mound or bell-shaped curves Ex: normal distribution 68% of data within + one SD of mean 95% of data within + two SD of mean 99. 7% of data within + three SD of mean
 Sample Variance
Sample Variance
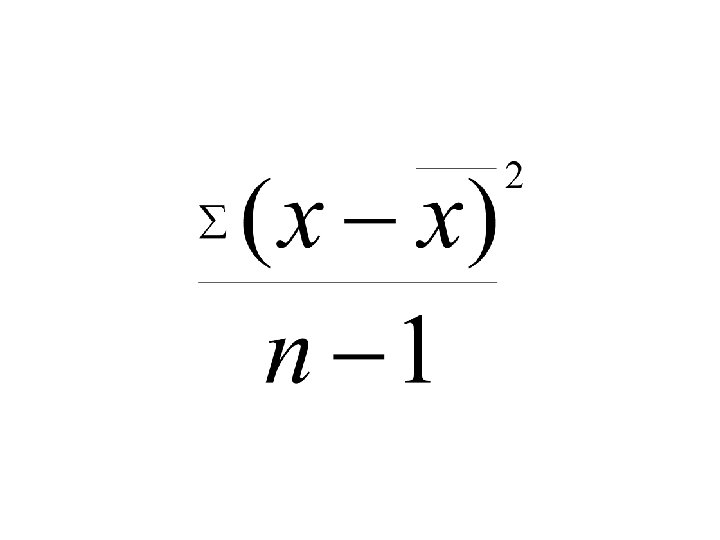
 Standard deviation = Square root of variance
Standard deviation = Square root of variance
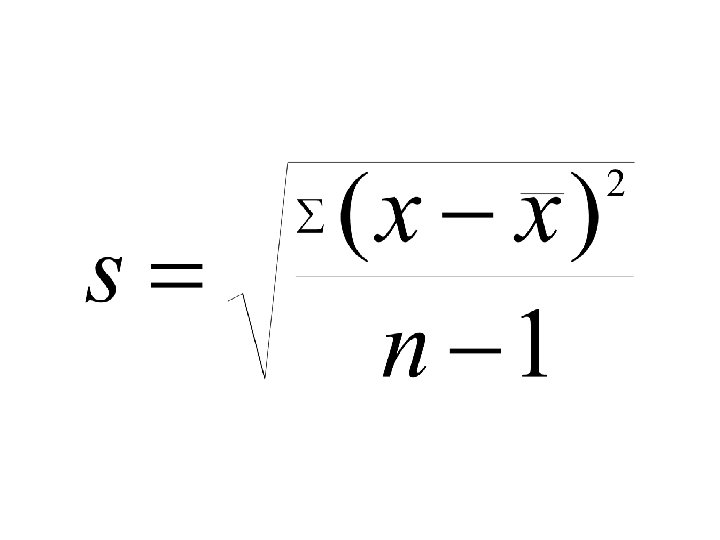
 Sample Standard Deviation X 6 6 7 8 13 Sum=40 Mean=40/5=8 6 -8=-2 7 -8=-1 8 -8=0 13 -8=5 Sum=0 (-2)= 4 4 (-1)= 1 0 (5)(5)= 25 Sum = 34
Sample Standard Deviation X 6 6 7 8 13 Sum=40 Mean=40/5=8 6 -8=-2 7 -8=-1 8 -8=0 13 -8=5 Sum=0 (-2)= 4 4 (-1)= 1 0 (5)(5)= 25 Sum = 34
 Standard Deviation Total variation = 34 • Sample variance = 34/4 = 8. 5 • Sample standard deviation = square root of 8. 5 = 2. 9
Standard Deviation Total variation = 34 • Sample variance = 34/4 = 8. 5 • Sample standard deviation = square root of 8. 5 = 2. 9
 Graphical Tools • Line chart: trend over time • Scatter diagram: relationship between two variables • Bar Chart: frequency for each category • Histogram: frequency for each class of measured data (graph of frequency distr) • Box Plot: graphical display based on quartiles, which divide data into 4 parts
Graphical Tools • Line chart: trend over time • Scatter diagram: relationship between two variables • Bar Chart: frequency for each category • Histogram: frequency for each class of measured data (graph of frequency distr) • Box Plot: graphical display based on quartiles, which divide data into 4 parts
 Top Ten #2 • Hypothesis Testing
Top Ten #2 • Hypothesis Testing
 Ho: Null Hypothesis • Population mean=µ • Population proportion=π • Never include sample statistic in hypothesis
Ho: Null Hypothesis • Population mean=µ • Population proportion=π • Never include sample statistic in hypothesis
 HA: Alternative Hypothesis • ONE TAIL ALTERNATIVE – Right tail: µ>number(smog ck) π>fraction(%defectives) Left tail: µ
HA: Alternative Hypothesis • ONE TAIL ALTERNATIVE – Right tail: µ>number(smog ck) π>fraction(%defectives) Left tail: µ
 Two-tail Alternative • Population mean not equal to number (too hot or too cold) • Population proportion not equal to fraction(% alcohol too weak or too strong)
Two-tail Alternative • Population mean not equal to number (too hot or too cold) • Population proportion not equal to fraction(% alcohol too weak or too strong)
 Reject null hypothesis if • • Absolute value of test statistic > critical value Reject Ho if |Z Value| > critical Z Reject Ho if | t Value| > critical t Reject Ho if p-value < significance level (note that direction of inequality is reversed) • Reject Ho if very large difference between sample statistic and population parameter in Ho
Reject null hypothesis if • • Absolute value of test statistic > critical value Reject Ho if |Z Value| > critical Z Reject Ho if | t Value| > critical t Reject Ho if p-value < significance level (note that direction of inequality is reversed) • Reject Ho if very large difference between sample statistic and population parameter in Ho
 Example: Smog Check • Ho: µ = 80 • HA: µ > 80 • If test statistic =2. 2 and critical value = 1. 96, reject Ho, and conclude that the population mean is likely > 80 • If test statistic = 1. 6 and critical value = 1. 96, do not reject Ho, and reserve judgment about Ho
Example: Smog Check • Ho: µ = 80 • HA: µ > 80 • If test statistic =2. 2 and critical value = 1. 96, reject Ho, and conclude that the population mean is likely > 80 • If test statistic = 1. 6 and critical value = 1. 96, do not reject Ho, and reserve judgment about Ho
 Type I vs Type II error • Alpha=α = P(type I error) = Significance level = probability you reject true null hypothesis • Ex: Ho: Defendant innocent • α = P(jury convicts innocent person) • Beta= β = P(type II error) = probability you do not reject a null hypothesis, given Ho false • β =P(jury acquits guilty person)
Type I vs Type II error • Alpha=α = P(type I error) = Significance level = probability you reject true null hypothesis • Ex: Ho: Defendant innocent • α = P(jury convicts innocent person) • Beta= β = P(type II error) = probability you do not reject a null hypothesis, given Ho false • β =P(jury acquits guilty person)
 Type I vs Type II Error Ho true Reject Ho Ho false Alpha =α = P(type I error) 1–β Do not reject Ho 1 -α Beta =β = P(type II error)
Type I vs Type II Error Ho true Reject Ho Ho false Alpha =α = P(type I error) 1–β Do not reject Ho 1 -α Beta =β = P(type II error)
 Top Ten #3 • Confidence Intervals: Mean and Proportion
Top Ten #3 • Confidence Intervals: Mean and Proportion
 Confidence Interval: Mean • Use normal distribution (Z table if): population standard deviation (sigma) known and either (1) or (2): (1) Normal population (2) Sample size > 30
Confidence Interval: Mean • Use normal distribution (Z table if): population standard deviation (sigma) known and either (1) or (2): (1) Normal population (2) Sample size > 30
 Confidence Interval: Mean • If normal table, then µ =(Σx/n)+ Z(σ/n 1/2), where n 1/2 is the square root of n
Confidence Interval: Mean • If normal table, then µ =(Σx/n)+ Z(σ/n 1/2), where n 1/2 is the square root of n
 Normal table • Tail =. 5(1 – confidence level) • NOTE! Different statistics texts have different normal tables • This review uses the tail of the bell curve • Ex: 95% confidence: tail =. 5(1 -. 95)=. 025 • Z. 025 = 1. 96
Normal table • Tail =. 5(1 – confidence level) • NOTE! Different statistics texts have different normal tables • This review uses the tail of the bell curve • Ex: 95% confidence: tail =. 5(1 -. 95)=. 025 • Z. 025 = 1. 96
 Example • n=49, Σx=490, σ=2, 95% confidence • µ = (490/49) + 1. 96(2/7) = 10 +. 56 • 9. 44 < µ < 10. 56
Example • n=49, Σx=490, σ=2, 95% confidence • µ = (490/49) + 1. 96(2/7) = 10 +. 56 • 9. 44 < µ < 10. 56
 Conf. Interval: Mean t distribution • Use if normal population but population standard deviation (σ) not known • If you are given the sample standard deviation (s), use t table, assuming normal population • If one population, n-1 degrees of freedom
Conf. Interval: Mean t distribution • Use if normal population but population standard deviation (σ) not known • If you are given the sample standard deviation (s), use t table, assuming normal population • If one population, n-1 degrees of freedom
 t distribution • µ = (Σx/n) + tn-1(s/n 1/2)
t distribution • µ = (Σx/n) + tn-1(s/n 1/2)
 Conf. Interval: Proportion • Use if success or failure (ex: defective or ok) Normal approximation to binomial ok if (n)(π) > 5 and (n)(1 -π) > 5, where n = sample size π= population proportion NOTE! NEVER use the t table if proportion!!
Conf. Interval: Proportion • Use if success or failure (ex: defective or ok) Normal approximation to binomial ok if (n)(π) > 5 and (n)(1 -π) > 5, where n = sample size π= population proportion NOTE! NEVER use the t table if proportion!!
 Confidence Interval: proportion • Π= p + Z(p(1 -p)/n)1/2 • Ex: 8 defectives out of 100, so p =. 08 and n = 100, 95% confidence Π=. 08 + 1. 96(. 08*. 92/100)1/2 =. 08 +. 05
Confidence Interval: proportion • Π= p + Z(p(1 -p)/n)1/2 • Ex: 8 defectives out of 100, so p =. 08 and n = 100, 95% confidence Π=. 08 + 1. 96(. 08*. 92/100)1/2 =. 08 +. 05
 Interpretation • If 95% confidence, then 95% of all confidence intervals will include the true population parameter • NOTE! Never use the term “probability” when estimating a parameter!! (ex: Do NOT say ”Probability that population mean is between 23 and 32 is. 95” because parameter is not a random variable)
Interpretation • If 95% confidence, then 95% of all confidence intervals will include the true population parameter • NOTE! Never use the term “probability” when estimating a parameter!! (ex: Do NOT say ”Probability that population mean is between 23 and 32 is. 95” because parameter is not a random variable)
 Point vs Interval Estimate • • • Point estimate: statistic (single number) Ex: sample mean, sample proportion Each sample gives different point estimate Interval estimate: range of values Ex: Population mean = sample mean + error Parameter = statistic + error
Point vs Interval Estimate • • • Point estimate: statistic (single number) Ex: sample mean, sample proportion Each sample gives different point estimate Interval estimate: range of values Ex: Population mean = sample mean + error Parameter = statistic + error
 Width of Interval • • • Ex: sample mean =23, error = 3 Point estimate = 23 Interval estimate = 23 + 3, or (20, 26) Width of interval = 26 -20 = 6 Wide interval: Point estimate unreliable
Width of Interval • • • Ex: sample mean =23, error = 3 Point estimate = 23 Interval estimate = 23 + 3, or (20, 26) Width of interval = 26 -20 = 6 Wide interval: Point estimate unreliable
 Wide interval if • (1) small sample size(n) • (2) large standard deviation(σ) • (3) high confidence interval (ex: 99% confidence interval wider than 95% confidence interval) If you want narrow interval, you need a large sample size or small standard deviation or low confidence level.
Wide interval if • (1) small sample size(n) • (2) large standard deviation(σ) • (3) high confidence interval (ex: 99% confidence interval wider than 95% confidence interval) If you want narrow interval, you need a large sample size or small standard deviation or low confidence level.
 Top Ten #4: Linear Regression • Regression equation: y=bo+b 1 x • y=dependent variable=predicted value • x= independent variable • bo=y-intercept =predicted value of y if x=0 • b 1=slope=regression coefficient =change in y per unit change in x
Top Ten #4: Linear Regression • Regression equation: y=bo+b 1 x • y=dependent variable=predicted value • x= independent variable • bo=y-intercept =predicted value of y if x=0 • b 1=slope=regression coefficient =change in y per unit change in x
 Slope vs correlation • Positive slope (b 1>0): positive correlation between x and y (y incr if x incr) • Negative slope (b 1<0): negative correlation (y decr if x incr) • Zero slope (b 1=0): no correlation(predicted value for y is mean of y), no linear relationship between x and y
Slope vs correlation • Positive slope (b 1>0): positive correlation between x and y (y incr if x incr) • Negative slope (b 1<0): negative correlation (y decr if x incr) • Zero slope (b 1=0): no correlation(predicted value for y is mean of y), no linear relationship between x and y
 Simple linear regression • Simple: one independent variable, one dependent variable • Linear: graph of regression equation is straight line
Simple linear regression • Simple: one independent variable, one dependent variable • Linear: graph of regression equation is straight line
 Coefficient of determination • R 2 = % of total variation in y that can be explained by variation in x • Measure of how close the linear regression line fits the points in a scatter diagram • R 2 = 1: max possible value: perfect linear relationship between y and x (straight line) • R 2 = 0: min value: no linear relationship
Coefficient of determination • R 2 = % of total variation in y that can be explained by variation in x • Measure of how close the linear regression line fits the points in a scatter diagram • R 2 = 1: max possible value: perfect linear relationship between y and x (straight line) • R 2 = 0: min value: no linear relationship
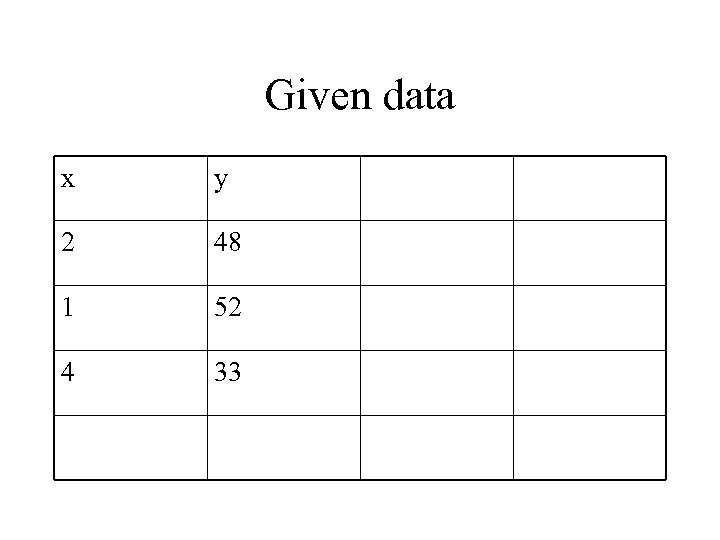
 example • Y = salary (female manager, in thousands of dollars) • X = number of children • n = number of observations
example • Y = salary (female manager, in thousands of dollars) • X = number of children • n = number of observations
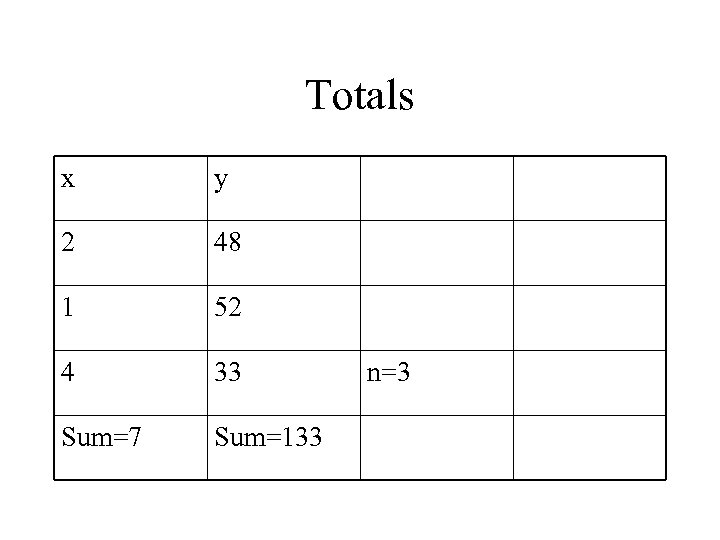
 Given data x y 2 48 1 52 4 33
Given data x y 2 48 1 52 4 33
 Totals x y 2 48 1 52 4 33 Sum=7 Sum=133 n=3
Totals x y 2 48 1 52 4 33 Sum=7 Sum=133 n=3
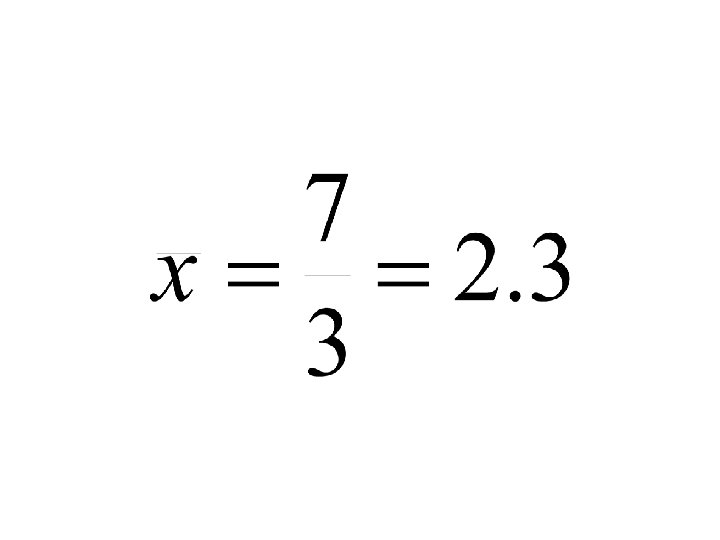
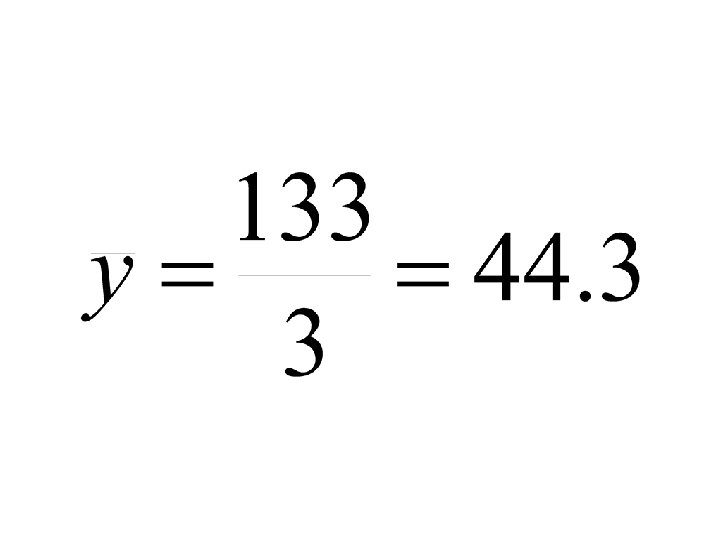
 Slope = -6. 500 • Method of Least Squares formulas not on 301 exam • B 1 = -6. 500 given
Slope = -6. 500 • Method of Least Squares formulas not on 301 exam • B 1 = -6. 500 given
 Interpret slope If one female manager has 1 more child than another, salary is $6500 lower
Interpret slope If one female manager has 1 more child than another, salary is $6500 lower
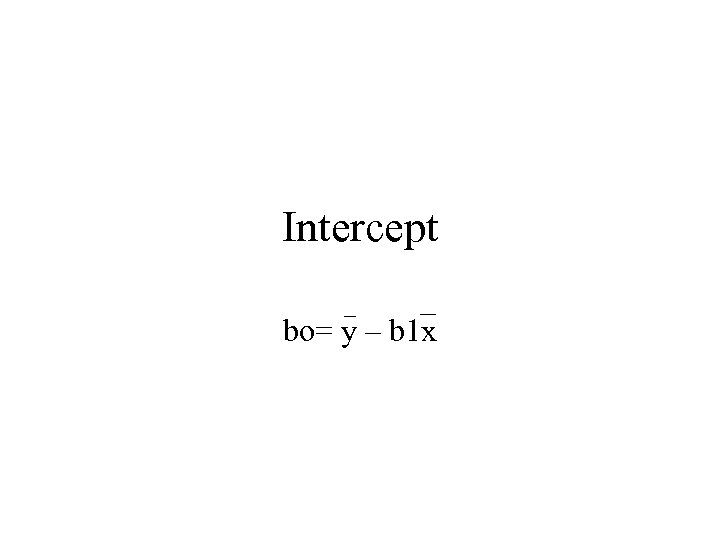 Intercept bo= y – b 1 x
Intercept bo= y – b 1 x
 Intercept bo=44. 33 -(-6. 5)(2. 33) = 59. 5
Intercept bo=44. 33 -(-6. 5)(2. 33) = 59. 5
 Interpret intercept If number of children is zero, expected salary is $59, 500
Interpret intercept If number of children is zero, expected salary is $59, 500
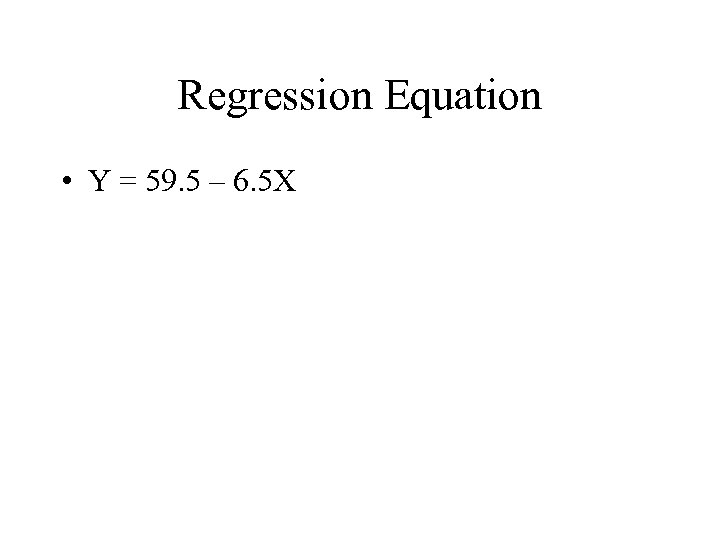 Regression Equation • Y = 59. 5 – 6. 5 X
Regression Equation • Y = 59. 5 – 6. 5 X
 Forecast salary if 3 children 59. 5 – 6. 5(3) = 40 $40, 000 = expected salary
Forecast salary if 3 children 59. 5 – 6. 5(3) = 40 $40, 000 = expected salary
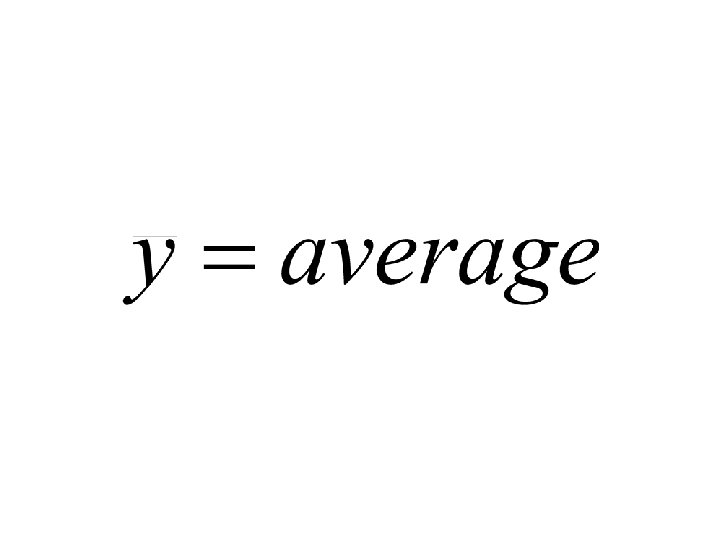
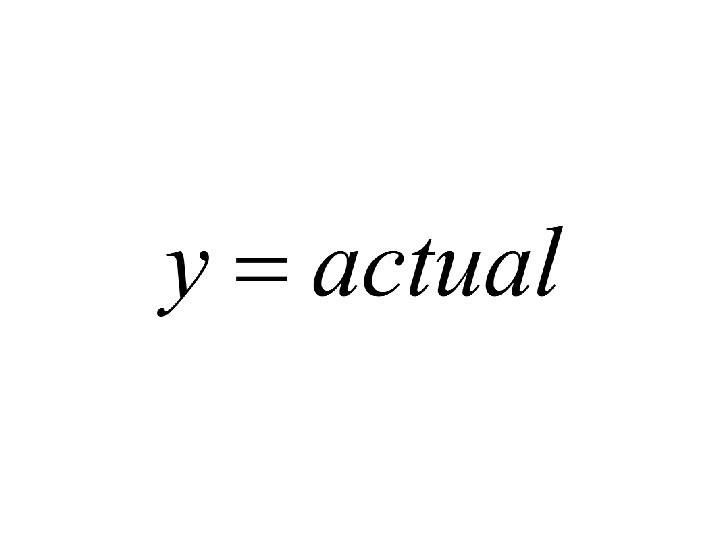
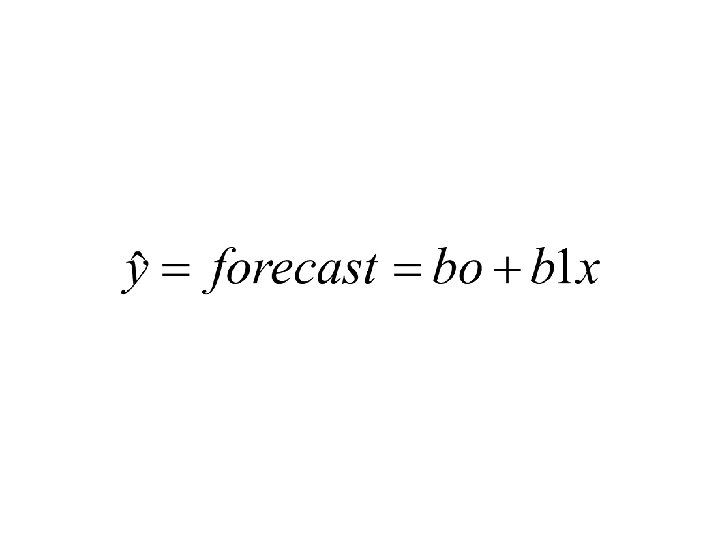
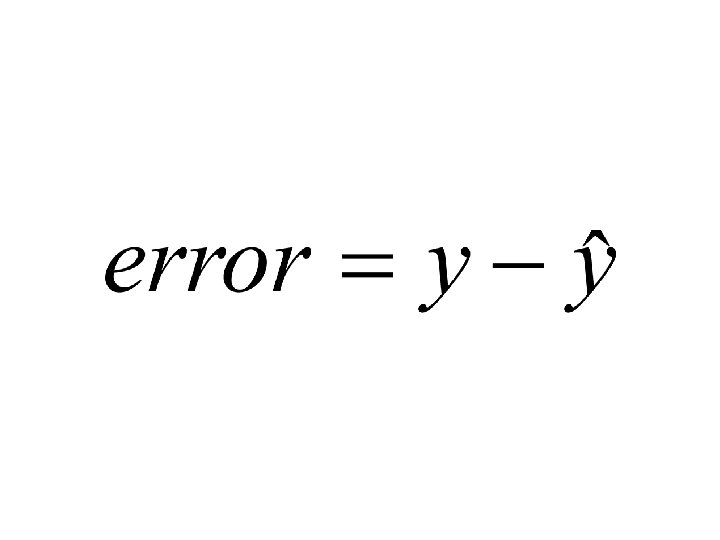
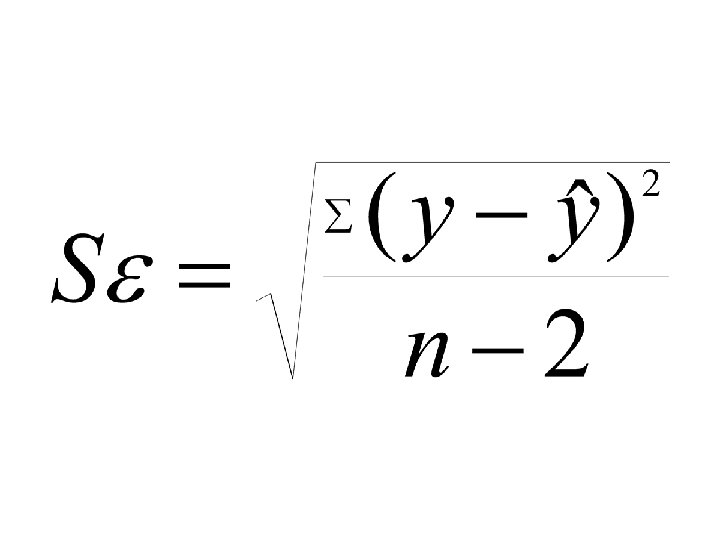
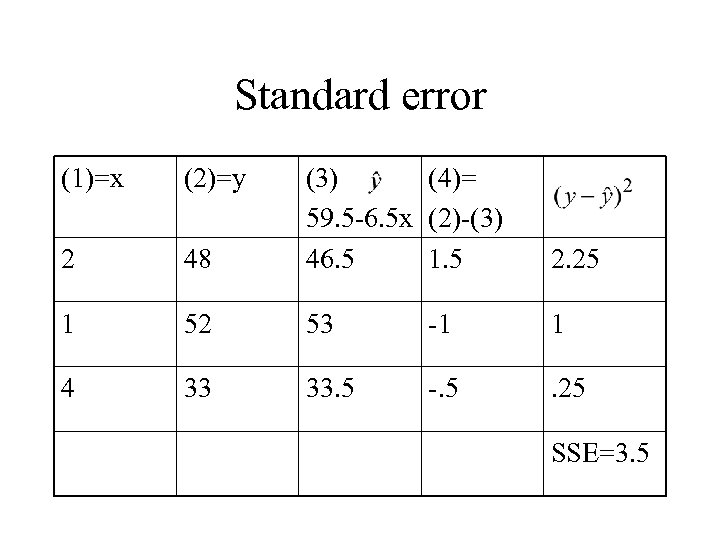 Standard error (1)=x (2)=y 48 (3) (4)= 59. 5 -6. 5 x (2)-(3) 46. 5 1. 5 2 2. 25 1 52 53 -1 1 4 33 33. 5 -. 5 . 25 SSE=3. 5
Standard error (1)=x (2)=y 48 (3) (4)= 59. 5 -6. 5 x (2)-(3) 46. 5 1. 5 2 2. 25 1 52 53 -1 1 4 33 33. 5 -. 5 . 25 SSE=3. 5
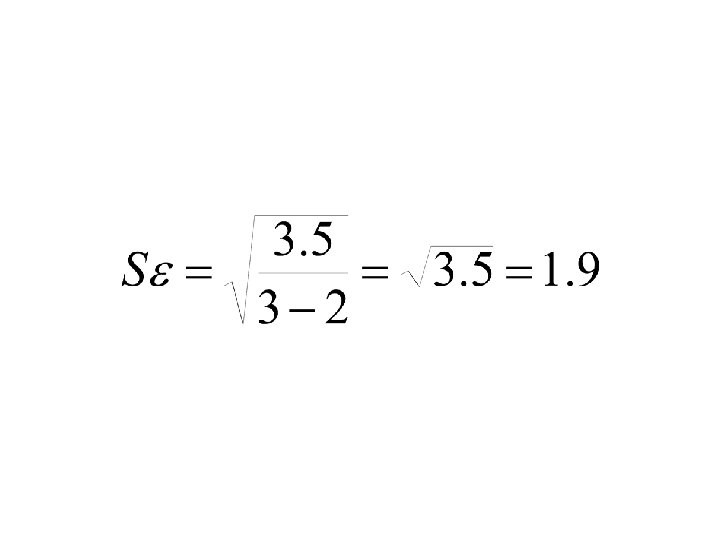
 Interpret Actual salary typically $1900 away from expected salary
Interpret Actual salary typically $1900 away from expected salary
 • • • Sources of Variation (V) Total V = Explained V + Unexplained V SS = Sum of Squares = V Total SS = Regression SS + Error SS SST = SSR + SSE SSR = Explained V, SSE = Unexplained
• • • Sources of Variation (V) Total V = Explained V + Unexplained V SS = Sum of Squares = V Total SS = Regression SS + Error SS SST = SSR + SSE SSR = Explained V, SSE = Unexplained
 Coefficient of Determination • R 2 = SSR SST • R 2 = 197 =. 98 200. 5 • Interpret: 98% of total variation in salary can be explained by variation in number of children
Coefficient of Determination • R 2 = SSR SST • R 2 = 197 =. 98 200. 5 • Interpret: 98% of total variation in salary can be explained by variation in number of children
 0< 2 R <1 • 0: No linear relationship since SSR=0 (explained variation =0) • 1: Perfect relationship since SSR = SST (unexplained variation = SSE = 0), but does not prove cause and effect
0< 2 R <1 • 0: No linear relationship since SSR=0 (explained variation =0) • 1: Perfect relationship since SSR = SST (unexplained variation = SSE = 0), but does not prove cause and effect
 R=Correlation Coefficient • Case 1: slope < 0 • R<0 • R is negative square root of coefficient of determination
R=Correlation Coefficient • Case 1: slope < 0 • R<0 • R is negative square root of coefficient of determination

 Our Example • Slope = b 1 = -6. 5 • R 2 =. 98 • R = -. 99
Our Example • Slope = b 1 = -6. 5 • R 2 =. 98 • R = -. 99
 Case 2: Slope > 0 • R is positive square root of coefficient of determination • Ex: R 2 =. 49 • R =. 70 • R has no interpretation • R overstates relationship
Case 2: Slope > 0 • R is positive square root of coefficient of determination • Ex: R 2 =. 49 • R =. 70 • R has no interpretation • R overstates relationship
 Caution • Nonlinear relationship (parabola, hyperbola, etc) can NOT be measured by R 2 • In fact, you could get R 2=0 with a nonlinear graph on a scatter diagram
Caution • Nonlinear relationship (parabola, hyperbola, etc) can NOT be measured by R 2 • In fact, you could get R 2=0 with a nonlinear graph on a scatter diagram
 R=correlation coefficient • Case 1: If b 1>0, R is the positive square root of the coefficient of determination • Ex#1: y = 4+3 x, R 2=. 36: R = +. 60 • Case 2: If b 1<0, R is the negative square root of the coefficient of determination • Ex#2: y = 80 -10 x, R 2=. 49: R = -. 70 • NOTE! Ex#2 has stronger relationship, as measured by coefficient of determination
R=correlation coefficient • Case 1: If b 1>0, R is the positive square root of the coefficient of determination • Ex#1: y = 4+3 x, R 2=. 36: R = +. 60 • Case 2: If b 1<0, R is the negative square root of the coefficient of determination • Ex#2: y = 80 -10 x, R 2=. 49: R = -. 70 • NOTE! Ex#2 has stronger relationship, as measured by coefficient of determination
 Extreme Values • R=+1: perfect positive correlation • R= -1: perfect negative correlation • R=0: zero correlation
Extreme Values • R=+1: perfect positive correlation • R= -1: perfect negative correlation • R=0: zero correlation
 Top Ten #5 • Expected Value = E(x) = Σx. P(x) = x 1 P(x 1) + x 2 P(x 2) +… Expected value is a weighted average, also a long-run average
Top Ten #5 • Expected Value = E(x) = Σx. P(x) = x 1 P(x 1) + x 2 P(x 2) +… Expected value is a weighted average, also a long-run average
 E(x) Example • Find the expected age at high school graduation if 11 were 17 years old, 80 were 18, and 5 were 19 • Step 1: 11+80+5=96
E(x) Example • Find the expected age at high school graduation if 11 were 17 years old, 80 were 18, and 5 were 19 • Step 1: 11+80+5=96
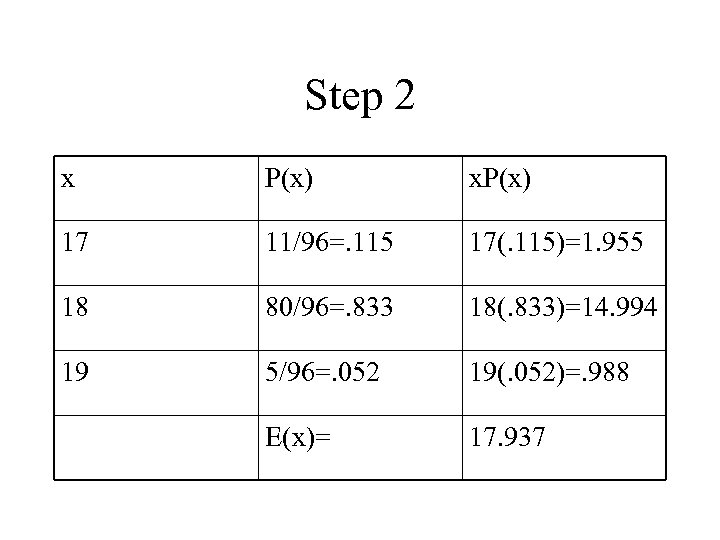 Step 2 x P(x) x. P(x) 17 11/96=. 115 17(. 115)=1. 955 18 80/96=. 833 18(. 833)=14. 994 19 5/96=. 052 19(. 052)=. 988 E(x)= 17. 937
Step 2 x P(x) x. P(x) 17 11/96=. 115 17(. 115)=1. 955 18 80/96=. 833 18(. 833)=14. 994 19 5/96=. 052 19(. 052)=. 988 E(x)= 17. 937
 Top Ten #6 • What distribution to use?
Top Ten #6 • What distribution to use?
 Use binomial distribution if: • Random variable (x) is number of successes in n trials • Each trial is success or failure • Independent trials • Constant probability of success (π) on each trial • Sampling with replacement (in practice, people may use binomial w/o replacement, but theory is with replacement)
Use binomial distribution if: • Random variable (x) is number of successes in n trials • Each trial is success or failure • Independent trials • Constant probability of success (π) on each trial • Sampling with replacement (in practice, people may use binomial w/o replacement, but theory is with replacement)
 Success vs failure • • Male vs female Defective vs ok Yes or no Pass (8 or more right answers) vs fail (fewer than 8) • Buy drink (21 or over) vs can’t buy drink
Success vs failure • • Male vs female Defective vs ok Yes or no Pass (8 or more right answers) vs fail (fewer than 8) • Buy drink (21 or over) vs can’t buy drink
 Binomial is discrete • Integer values • 0, 1, 2, …n • Binomial is often skewed, but may be symmetric
Binomial is discrete • Integer values • 0, 1, 2, …n • Binomial is often skewed, but may be symmetric
 Normal Distribution • • Continuous, bell-shaped, symmetric Mean=median=mode Measurement (dollars, inches, years) Cumulative probability under normal curve : use Z table if you know population mean and population standard deviation • Sample mean: use Z table if you know population standard deviation and either normal population or n > 30
Normal Distribution • • Continuous, bell-shaped, symmetric Mean=median=mode Measurement (dollars, inches, years) Cumulative probability under normal curve : use Z table if you know population mean and population standard deviation • Sample mean: use Z table if you know population standard deviation and either normal population or n > 30
 t distribution • • Continuous, bell-shaped, symmetric Applications similar to normal More spread out than normal Use t if normal population but population standard deviation not known • Degrees of freedom = df = n-1 if estimating the mean of one population • t approaches z as df increases
t distribution • • Continuous, bell-shaped, symmetric Applications similar to normal More spread out than normal Use t if normal population but population standard deviation not known • Degrees of freedom = df = n-1 if estimating the mean of one population • t approaches z as df increases
 Top Ten #7 • P-value = probability of getting a sample statistic as extreme (or more extreme) than the sample statistic you got from your sample
Top Ten #7 • P-value = probability of getting a sample statistic as extreme (or more extreme) than the sample statistic you got from your sample
 P-value example: 1 tail test • • Ho: µ = 40 HA: µ > 40 Sample mean = 43 P-value = P(sample mean > 43, given Ho true) • Reject Ho if p-value < α (significance level)
P-value example: 1 tail test • • Ho: µ = 40 HA: µ > 40 Sample mean = 43 P-value = P(sample mean > 43, given Ho true) • Reject Ho if p-value < α (significance level)
 Two cases • Suppose α =. 05 • Case 1: p-value =. 02, then reject Ho (unlikely Ho is true; you believe population mean > 40) • Case 2: p-value =. 08, then do not reject Ho (Ho may be true; you have reason to believe that population mean may be 40)
Two cases • Suppose α =. 05 • Case 1: p-value =. 02, then reject Ho (unlikely Ho is true; you believe population mean > 40) • Case 2: p-value =. 08, then do not reject Ho (Ho may be true; you have reason to believe that population mean may be 40)
 P-value example: 2 tail test • • Ho: µ = 70 HA: µ not equal to 70 Sample mean = 72 If 2 -tails, then P-value = 2*P(sample mean > 72)=2(. 04)=. 08 If α =. 05, p-value > α, so do not reject Ho
P-value example: 2 tail test • • Ho: µ = 70 HA: µ not equal to 70 Sample mean = 72 If 2 -tails, then P-value = 2*P(sample mean > 72)=2(. 04)=. 08 If α =. 05, p-value > α, so do not reject Ho
 Top Ten #8 • Variation creates uncertainty
Top Ten #8 • Variation creates uncertainty
 No variation • • • Certainty, exact prediction Standard deviation = 0 Variance = 0 All data exactly same Example: all workers in minimum wage job
No variation • • • Certainty, exact prediction Standard deviation = 0 Variance = 0 All data exactly same Example: all workers in minimum wage job
 High variation • Uncertainty, unpredictable • High standard deviation • Ex#1: Workers in downtown L. A. have variation between CEOs and garment workers • Ex#2: New York temperatures in spring range from below freezing to very hot
High variation • Uncertainty, unpredictable • High standard deviation • Ex#1: Workers in downtown L. A. have variation between CEOs and garment workers • Ex#2: New York temperatures in spring range from below freezing to very hot
 Comparing standard deviations • Temperature Example • Beach city: small standard deviation (single temperature reading close to mean) • High Desert city: High standard deviation (hot days, cool nights in spring)
Comparing standard deviations • Temperature Example • Beach city: small standard deviation (single temperature reading close to mean) • High Desert city: High standard deviation (hot days, cool nights in spring)
 Standard error of the mean • Standard deviation of sample mean = standard deviation/square root of n Ex: standard deviation = 10, n =4, so standard error of the mean = 10/2= 5 Note that 5<10, so standard error < standard deviation As n increases, standard error decreases
Standard error of the mean • Standard deviation of sample mean = standard deviation/square root of n Ex: standard deviation = 10, n =4, so standard error of the mean = 10/2= 5 Note that 5<10, so standard error < standard deviation As n increases, standard error decreases
 Sampling Distribution • Expected value of sample mean = population mean, but an individual sample mean could be smaller or larger than the population mean • Population mean is a constant parameter, but sample mean is a random variable • Sampling distribution is distribution of sample means
Sampling Distribution • Expected value of sample mean = population mean, but an individual sample mean could be smaller or larger than the population mean • Population mean is a constant parameter, but sample mean is a random variable • Sampling distribution is distribution of sample means
 Example • Mean age of all students in the building is population mean • Each classroom has a sample mean • Distribution of sample means from all classrooms is sampling distribution
Example • Mean age of all students in the building is population mean • Each classroom has a sample mean • Distribution of sample means from all classrooms is sampling distribution
 Central Limit Theorem • If population standard deviation is known, sampling distribution of sample means is normal if n > 30 • CLT applies even if original population is skewed
Central Limit Theorem • If population standard deviation is known, sampling distribution of sample means is normal if n > 30 • CLT applies even if original population is skewed
 Top Ten #9 • Population vs sample
Top Ten #9 • Population vs sample
 Population • Collection of all items(all light bulbs made at factory) • Parameter: measure of population (1)population mean(average number of hours in life of all bulbs) (2)population proportion(% of all bulbs that are defective)
Population • Collection of all items(all light bulbs made at factory) • Parameter: measure of population (1)population mean(average number of hours in life of all bulbs) (2)population proportion(% of all bulbs that are defective)
 Sample • Part of population(bulbs tested by inspector) • Statistic: measure of sample = estimate of parameter (1) sample mean(average number of hours in life of bulbs tested by inspector) (2) sample proportion(% of bulbs in sample that are defective)
Sample • Part of population(bulbs tested by inspector) • Statistic: measure of sample = estimate of parameter (1) sample mean(average number of hours in life of bulbs tested by inspector) (2) sample proportion(% of bulbs in sample that are defective)
 Top Ten #10 • Qualitative vs quantitative
Top Ten #10 • Qualitative vs quantitative
 Qualitative • Categorical data success vs failure ethnicity marital status color zip code 4 star hotel in tour guide
Qualitative • Categorical data success vs failure ethnicity marital status color zip code 4 star hotel in tour guide
 Qualitative • If you need an “average”, do not calculate the mean • However, you can compute the mode (“average” person is married, buys a blue car made in America)
Qualitative • If you need an “average”, do not calculate the mean • However, you can compute the mode (“average” person is married, buys a blue car made in America)
 Quantitative • 2 cases • Case 1: discrete • Case 2: continuous
Quantitative • 2 cases • Case 1: discrete • Case 2: continuous
 Discrete (1) integer values (0, 1, 2, …) (2) example: binomial (3) finite number of possible values (4) counting (5) number of brothers (6) number of cars arriving at gas station
Discrete (1) integer values (0, 1, 2, …) (2) example: binomial (3) finite number of possible values (4) counting (5) number of brothers (6) number of cars arriving at gas station
 Continuous • Real numbers, such as decimal values ($22. 22) • Examples: Z, t • Infinite number of possible values • Measurement • Miles per gallon, distance, duration of time
Continuous • Real numbers, such as decimal values ($22. 22) • Examples: Z, t • Infinite number of possible values • Measurement • Miles per gallon, distance, duration of time
 Graphical tools • Pie chart or bar chart: qualitative • Joint frequency table: qualitative (relate marital status vs zip code) • Scatter diagram: quantitative (distance from CSUN vs duration of time to reach CSUN)
Graphical tools • Pie chart or bar chart: qualitative • Joint frequency table: qualitative (relate marital status vs zip code) • Scatter diagram: quantitative (distance from CSUN vs duration of time to reach CSUN)
 Hypothesis testing Confidence intervals • Quantitative: Mean • Qualitative: Proportion
Hypothesis testing Confidence intervals • Quantitative: Mean • Qualitative: Proportion


