9c9b924b60b1b94cf66d56d043d63abd.ppt
- Количество слайдов: 45

Top-Down Parsing using Regular Expressions A seminar by Brian Westphal

Questions and comments • Please feel free to interrupt at any time throughout this presentation to make comments and ask questions. • However, if there is a question that you feel might take more than a minute or two to explain, please wait until I specifically ask for questions.

Part I General Discussion

What is a top-down parser? • Starts at the most general case (I. e. source code for a computer program). • Tries to reach more specific cases (I. e. variable, loop, init statement, etc. ) until a string is broken down into its smallest elements. • End result is a tree of parts, each part described by a rule.
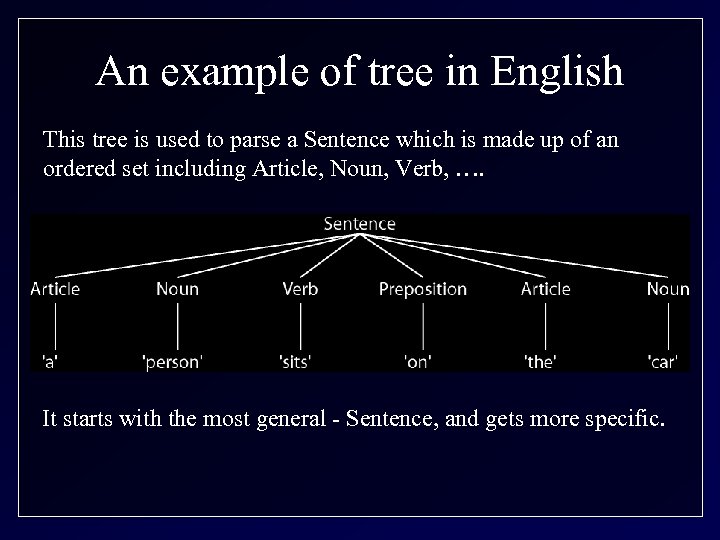
An example of tree in English This tree is used to parse a Sentence which is made up of an ordered set including Article, Noun, Verb, …. It starts with the most general - Sentence, and gets more specific.

The grammar (or rules) in BNF Bachus-Naur Form English : : = Sentence* Sentence : : = (Article S)? Noun S Verb S (Preposition S)? (Article S)? Noun '/. ' Article : : = 'a' | 'an' | 'the' Noun : : = 'house' | 'car' | 'person' Verb : : = 'plays' | 'sits' | 'goes' Preposition : : = 'on' | 'over' | 'above' S : : = ' '

Regular Expressions v Grammars • Regular expressions compose the most specific elements in a grammar (I. e. ‘a’, ‘car’, etc). • BNF notations allows rules to be combined in a regular expression-like manner. • The grammar holds a collection of rules which eventually terminate in regular expressions.

The process of parsing, by example • We want to parse the following string with our example grammar: “A person sits on the car. A person sits on the house. ” • (ignore capitalization for now) • Start with most basic rule, English (not denoted by graph)

• Try to match the string to rule English. • 1. English is equal to Sentence* • In a loop (until all of string is exhausted or failure is reached) match each Sentence • 2. Sentence is equal to (Article S)? Noun S … • Match each sub-rule where “(Article S)? ” is a single sub-rule, Noun is a single sub-rule, etc. • 3. Article is equal to ‘a’|’an’|’the’

• 4. Try to match string with ‘a’, ‘an’, and ‘the’ – A match is found with ‘a’ (the longest of the acceptable matches). • 5. Try to match remaining string (chop off ‘a’) with rule S. • 6. S is equal to ‘ ‘ (a single space). A match is found with ‘ ‘. • 7. Try to match remaining string with rule Noun. • 8. Continue pattern.

What happens if a rule does not match? • It depends on the situation. • If a rule is followed by a * or a ? The rule will never fail by the fact that it is not required. • Otherwise, there is an error in the data. Report an error message or try to fix it.

Failure/Success Examples • • “sits on the car. ” failure (noun, space) “person sits on the car. ” success “person sits on the car” failure (period) “a car goes over person. ” success

Part II Goals and Requirements

List of goals • Parse any EBNF grammar compatible data such as source code. • Use and extend our existing regular expression classes. • Output a syntax tree describing the full structure of the parsed data. • For the end result we also wish to develop a tool that builds parsers for us (based on specified EBNF grammar files).

Goal Requirements • A class to process EBNF rules (also called productions). • A class to process more basic rules. • A class to process regular expressions as rules. • A class to act as the tree structure.

A BNF grammar describing EBNF grammars • Show EBNF. grammar

In other words • An EBNF grammar (Extended Bachus Naur Form) supports a subtraction operation on top of regular BNF functionality. • Subtraction (A-B) implies that for the same section of data the system matches A but does not match B. Clearly this is not a typical regular expressionlike operation.

Part III Basic Class Descriptions

RETree • The structure for the syntax tree. Each node in an RETree is either an RETree or an RE (regular expression). • Each node may also be associated with a type (I. e. English, Sentence, Noun, etc. )

REProcessor • Handles regular expressions in binary or unary operations as parts of productions. • Binary modes (operations) are: andnot, or, follow • Unary modes are: follow, star, plus, maybe

Sub. Production. Processor • Extension of REProcessor. • Handles REProcessors and references to other productions and subproductions. • In this way the unary and binary operations can be used for productions in general. • Assigns a type in the tree to matching values.

Production. Processor • Extension of Sub. Production. Processor. • Contains a reference array to the other productions. • Breaks down a single rule into subproductions by splitting rule in more manageable (unary or binary) pieces (a. k. a. subproductions).

Part IV Code Overview

Coding RETree • Take advantage of Java’s excellent polymorphism. • RETree has two properties: Object branches & String type • branches can be of type String or Linked. List.

Useful function in RETree • Collapse – Returns a single string of the section matched by the RETree (I. e. for English in our previous example, it would be the two sentences. For Sentence it would be a whole sentence, etc. ) • Size – Returns the length of the string (so that we can know how much of the input we have used).

Coding REProcessor • Make some contants for the modes (operations). • REProcessor has three properties: Object A, Object B, & byte mode • A & B can be of type REProcessor or RE. • Mode will be one of the contant values.

Useful functions in REProcessor • beginning. Matches – Takes a string of input and returns an RETree if the REProcessor matches the beginning of the input (returns the longest match if multiple matches exist). Returns null if no match is found. • evaluate – Calls beginning. Matches for either REProcessors or REs

More on beginning. Matches • Must perform actions for each mode. • Calls evaluate on substrings of the input for A and/or B as many times as is necessary to find the longest match or failure. • Mode follow has both a unary and binary operation. • In unary mode it checks if A matches, in binary mode it checks if A matches then B matches the section immediately following A.

Coding Sub. Production. Processor • Sub. Production. Processor has two properties: String type Sub. Production. Processor [] subproduction • Uses the super functions for beginning. Matches and evaluate (with a few minor changes). • Not much code to this class.

Changes to beginning. Matches • First calls the super classes beginning. Matches function. If it is successful and no type has been assigned to the resulting tree, a type is added.

Changes to evaluate • If the automata passed to evaluate is of type Integer, the function gets the subproduction associated with the value and calls beginning. Matches for it. • Otherwise, it calls the super classes evaluate function.
![Coding Production. Processor • Production. Processor has three properties: Production. Processor [] production Linked. Coding Production. Processor • Production. Processor has three properties: Production. Processor [] production Linked.](https://present5.com/presentation/9c9b924b60b1b94cf66d56d043d63abd/image-32.jpg)
Coding Production. Processor • Production. Processor has three properties: Production. Processor [] production Linked. List subproductionlist int numsubproductions • The production array contains references to all other productions and the subproductions for the current production.

• subproductionlist holds 5 -tuples describing subproductions. These are only copied into actual subproductions during the Initialize. Processors function call. • numsuproductions holds the number of subproductions currently in use (incremented duing Build. Sub. Production. Processors function call).

A note about Production. Processor • Pieces to be matched by Production. Processor are passed in chunks. This way, special characters are easy to process. For example, instead of passing the rule matched by “(hello)? ” we would pass “(“, “hello”, “)”, “? ”. To search for parentheses and the question mark in this way is much quicker.

Useful functions in Production. Processor • Initialize. Processors – Adds intermediate subproduction 5 -tuples to the production array so that subproductions and productions are regarded as inherently similar items. This takes great advantage of Java’s excellent polymorphism.

• Build. Sub. Production. Processors – Builds the intermedie 5 -tuples representing the subproductions. This is the first step in a rather complex series of function calls which break down the production into unary and/or binary pieces. – It begins by splitting the rule on or operations (the pipe symbol). – Following order of operations, it then splits on the minus operation leaving groups without having to worry about or and minus operations. – No more detail will be provided about this sequence as it is too complicated for one class period.

Changes to beginning. Matches • Calls beginning. Matches for the first subproduction (as they are linked together, this will eventually call beginning. Matches for all subproductions). • A type is also assigned if none is available when the matching RETree is returned.

Part V Building a Parser Generator

Parsing an EBNF grammar • To build a parser generator we must first complete our parser by making a class to parse EBNF grammar data. • We have already seen the BNF grammar for EBNF grammars.

• • • • • • • rule : : = symbol whitespace eq whitespace expression whitespace : : = '[t ]*' symbol : : = '[a-z. A-Z 0 -9]+' re : : = hex. Character | character. List | standard. RE //re supporting rules: hex. Character : : = '/#x[0 -9 A-F]+' character. List : : = lbracket character. List 1? rbracket character. List 1 : : = character. List 2 | character. List 2 character. List 1 character. List 2 : : = '[^/]//]' | escape. Sequence standard. RE : : = single. Quote standard. RE 1? single. Quote standard. RE 1 : : = standard. RE 2 | standard. RE 2 standard. RE 1 standard. RE 2 : : = '[^/'//]' | escape. Sequence : : = '//. ' lbracket : : = '/[' rbracket : : = '/]' single. Quote : : = '/'' //---------------------------------------eq : : = ': : =' expression : : = group (whitespace or whitespace expression)? (whitespace or whitespace epsilon)? group : : = sequence (whitespace minus whitespace group)? sequence : : = sequence. LHS modifier? whitespace sequence? sequence. LHS : : = symbol | re | lparen whitespace expression whitespace rparen modifier : : = '[*+? ]' lparen : : = '/(' rparen : : = '/)' minus : : = '/-' or : : = '/|' epsilon : : = '_'
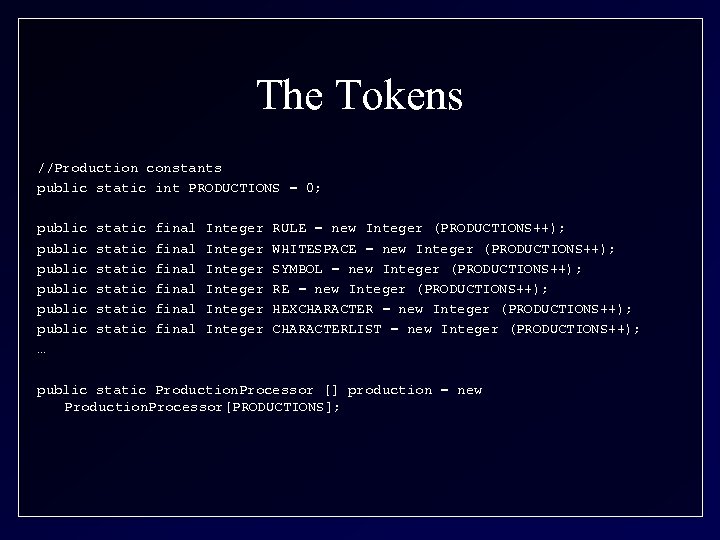
The Tokens //Production constants public static int PRODUCTIONS = 0; public public … static static final final Integer Integer RULE = new Integer (PRODUCTIONS++); WHITESPACE = new Integer (PRODUCTIONS++); SYMBOL = new Integer (PRODUCTIONS++); RE = new Integer (PRODUCTIONS++); HEXCHARACTER = new Integer (PRODUCTIONS++); CHARACTERLIST = new Integer (PRODUCTIONS++); public static Production. Processor [] production = new Production. Processor[PRODUCTIONS];
![The Productions Object [] parameters; parameters = new Object[5]; parameters[0] = SYMBOL; parameters[1] = The Productions Object [] parameters; parameters = new Object[5]; parameters[0] = SYMBOL; parameters[1] =](https://present5.com/presentation/9c9b924b60b1b94cf66d56d043d63abd/image-42.jpg)
The Productions Object [] parameters; parameters = new Object[5]; parameters[0] = SYMBOL; parameters[1] = WHITESPACE; parameters[2] = EQ; parameters[3] = WHITESPACE; parameters[4] = EXPRESSION; //rule : : = symbol whitespace eq whitespace expression production[RULE. int. Value ()] = new Production. Processor (production, "rule", parameters); parameters = new Object[1]; parameters[0] = "[t ]*"; //whitespace : : = '[t ]*' production[WHITESPACE. int. Value ()] = new Production. Processor (production, "whitespace", parameters); • Continue with this process for each rule.

Make sure to call Initialize. Processors //Initializing production processors for (int index = 0; index < production. length; index++) { production[index]. Initialize. Processors (); }

Continuing On… • That is pretty much it for the foundations of the parser generator. • Actually writing the parser generator to do what you want is up to you. I will show you my code (or you can download it from www. fokno. org), but it is too difficult to present line by line.

The End • Thank you for coming. Please feel free to ask questions and/or make comments at this time. • Be sure to visit www. fokno. org to download a copy of the discussed source code.
9c9b924b60b1b94cf66d56d043d63abd.ppt