Tools for Automated Verification of Concurrent Software Tevfik

Скачать презентацию Tools for Automated Verification of Concurrent Software Tevfik

1111f51039a28e18503a8ed20280c754.ppt

Количество слайдов: 94

Tools for Automated Verification of Concurrent Software Tevfik Bultan Department of Computer Science University of California, Santa Barbara bultan@cs. ucsb. edu http: //www. cs. ucsb. edu/~bultan/composite/

Summary • Goal: Building reliable concurrent software • Sub-goals: – Developing reliable concurrency controllers in Java – Developing reliable concurrent linked lists • Approach: Model Checking • Specification Language: Action Language • Tools: – Composite Symbolic Library – Action Language Verifier

Students Joint work with my students: • Tuba Yavuz-Kahveci • Constantinos Bartzis

Outline • • Difficulties in concurrent programming Action Language Composite Symbolic Library Application to concurrency controllers Application to concurrent linked lists Related work Current and future work

Difficulties in Concurrent Programming • Concurrent programming is difficult and error prone – In sequential programming you only worry about the states of the variables – In concurrent programming you also have to worry about the states of the threads • State space increases exponentially with the number of threads

Concurrent Programming in Java • Java uses a variant of monitor programming • Synchronization using locks – Each object has a lock synchronized(o) {. . . } • Coordination using condition variables – Objects can be used as condition variables synchronized (cond. Var){ while (!cond. Exp) wait(cond. Var); . . . notify. All(cond. Var); }

Dangers in Java Concurrency • Nested locks synchronized m(other) { other. m(); } Thread 1: run() { o 1. m(o 2); } Thread 2: run() { o 2. m(o 1); } Thread 1 o 1 lock Thread 2 lock o 2

Dangers in Java Concurrency • Missed notification notify(cond. Var); • Forgotten condition check if(!cond. Exp) wait(cond. Var); • Dependency among multiple condition variables can be complicated – Conservative notification and condition check Inefficient – Optimizing the notification and condition checks Error prone

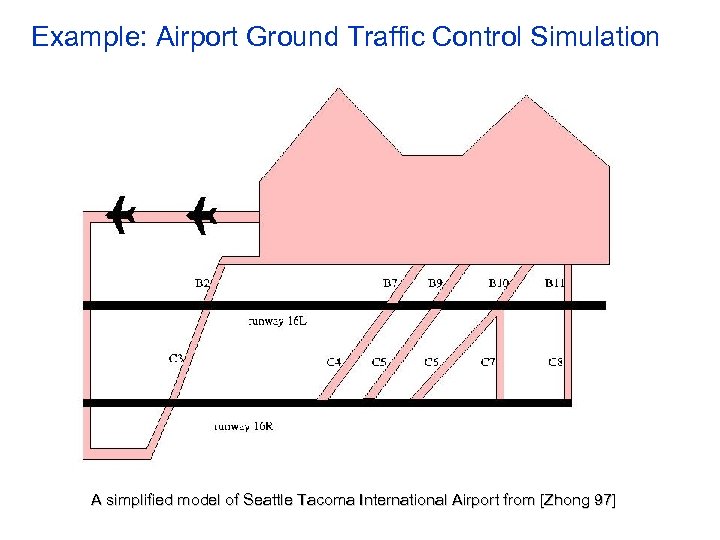Example: Airport Ground Traffic Control Simulation A simplified model of Seattle Tacoma International Airport from [Zhong 97]

Control Logic • An airplane can land using 16 R only if no airplane is using 16 R at the moment • An airplane can takeoff using 16 L only if no airplane is using 16 L at the moment • An airplane taxiing on one of the exits C 3 -C 8 can cross runway 16 L only if no airplane is taking off at the moment • An airplane can start using 16 L for taking off only if none of the crossing exits C 3 -C 8 is occupied at the moment (arriving airplanes have higher priority) • Only one airplane can use a taxiway at a time

Java Implementation • Simulate behavior of each airplane with a thread • Use a monitor (a Java class) – private variables for number of airplanes on each runway and each taxiway – methods of the monitor enforce the control logic • Each thread calls the methods of the monitor based on the airport layout to move from one point to the next

$Example Implementation public synchronized void C 8_To_B 11 A() { while (!((num. RW 16$ Example Implementation public synchronized void C 8_To_B 11 A() { while (!((num. RW 16 L == 0) && (num. B 11 A == 0))) wait(); num. C 8 = num. C 8 - 1; num. B 11 A = num. B 11 A + 1; notify. All(); } • This code is not efficient since every thread wakes up every other thread • Using separate condition variables complicates the synchronization – nested locks

Difficulties In Implementing Concurrent Linked Lists • Linked list manipulation is difficult and error prone – State of the heap: unbounded • State space: – Sequential programming • states of the variables – Concurrent programming • states of the variables • states of the threads – Concurrent linked lists • states of the variables • states of the threads • state of the heap

Examples • singly linked lists n 1 prev • doubly linked lists • stack • queue top first n 2 next n 1 next n 2 prev n 1 next n 2 next last next • single lock • double lock – allows concurrent inserts and deletes next

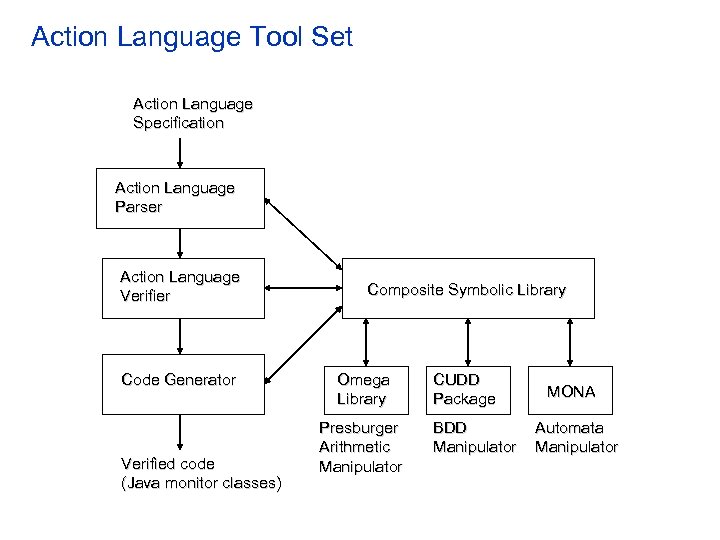Action Language Tool Set Action Language Specification Action Language Parser Action Language Verifier Code Generator Verified code (Java monitor classes) Composite Symbolic Library Omega Library Presburger Arithmetic Manipulator CUDD Package BDD Manipulator MONA Automata Manipulator

Action Language [Bultan, ICSE 00], [Bultan, Yavuz-Kahveci, ASE 01] • A state based language – Actions correspond to state changes • States correspond to valuations of variables – boolean – enumerated – integer (possibly unbounded) – heap variables (i. e. , pointers) • Parameterized constants – specifications are verified for every possible value of the constant

Action Language • Transition relation is defined using actions – Atomic actions: Predicates on current and next state variables – Action composition: • asynchronous (|) or synchronous (&) • Modular – Modules can have submodules – A module is defined as asynchronous and/or synchronous compositions of its actions and submodules

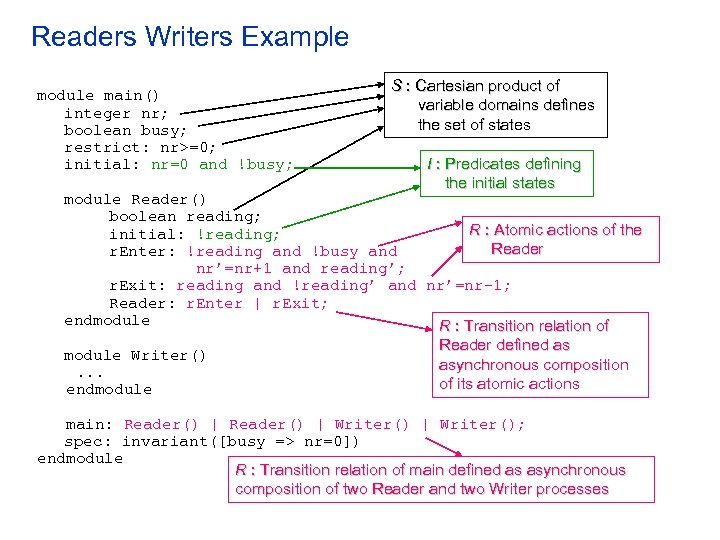Readers Writers Example module main() integer nr; boolean busy; restrict: nr>=0; initial: nr=0 and !busy; S : Cartesian product of variable domains defines the set of states I : Predicates defining the initial states module Reader() boolean reading; R : Atomic actions of the initial: !reading; Reader r. Enter: !reading and !busy and nr’=nr+1 and reading’; r. Exit: reading and !reading’ and nr’=nr-1; Reader: r. Enter | r. Exit; endmodule R : Transition relation of Reader defined as module Writer() asynchronous composition. . . of its atomic actions endmodule main: Reader() | Writer(); spec: invariant([busy => nr=0]) endmodule R : Transition relation of main defined as asynchronous composition of two Reader and two Writer processes

Which Symbolic Representation to Use? BDDs • canonical and efficient representation for Boolean logic formulas • can only encode finite sets x y {(T, T), (T, F), (F, T)} F x a > 0 b = a+1 T y F F Linear Arithmetic Constraints • can encode infinite sets • two representations – polyhedral representation – automata representation • mapping booleans to integers is not an efficient encoding T T {(1, 2), (2, 3), (3, 4), . . . }

Composite Model Checking [Bultan, Gerber, League ISSTA 98, TOSEM 00] • Map each variable type to a symbolic representation – Map boolean and enumerated types to BDD representation – Map integer type to a linear arithmetic constraint representation • Use a disjunctive representation to combine different symbolic representations: composite representation • Each disjunct is a conjunction of formulas represented by different symbolic representations – we call each disjunct a composite atom

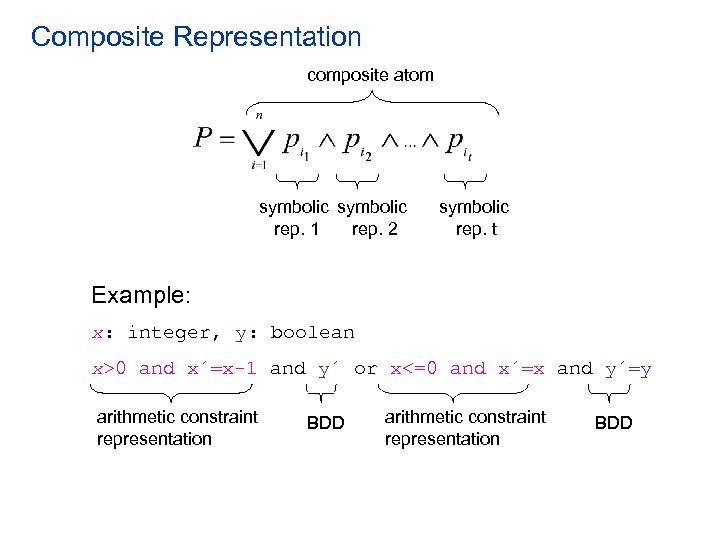Composite Representation composite atom symbolic rep. 1 rep. 2 symbolic rep. t Example: x: integer, y: boolean x>0 and x´ x-1 and y´ or x<=0 and x´ x and y´ y arithmetic constraint representation BDD

Composite Symbolic Library [Yavuz-Kahveci, Tuncer, Bultan TACAS 01], [Yavuz-Kahveci, Bultan Fro. Cos 02, STTT 03] • Uses a common interface for each symbolic representation • Easy to extend with new symbolic representations • Enables polymorphic verification • Multiple symbolic representations: – As a BDD library we use Colorado University Decision Diagram Package (CUDD) [Somenzi et al] – As an integer constraint manipulator we use Omega Library [Pugh et al]

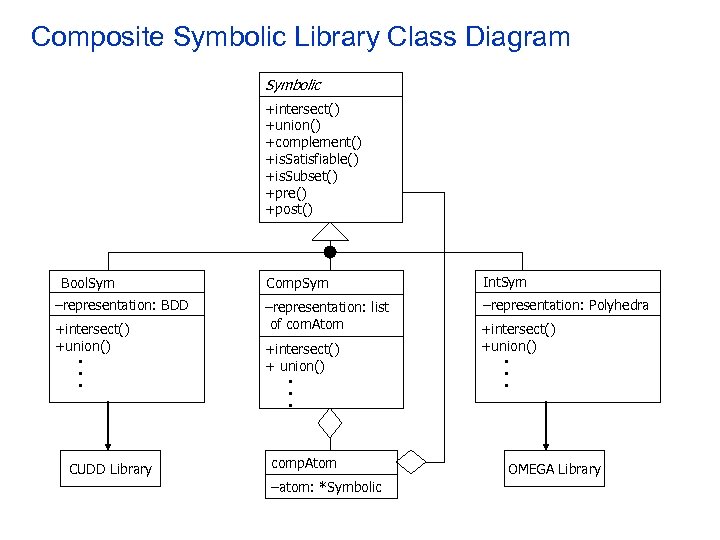Composite Symbolic Library Class Diagram Symbolic +intersect() +union() +complement() +is. Satisfiable() +is. Subset() +pre() +post() Bool. Sym –representation: BDD +intersect() +union() • • • CUDD Library Comp. Sym Int. Sym –representation: list of com. Atom –representation: Polyhedra +intersect() + union() • • • comp. Atom –atom: *Symbolic +intersect() +union() • • • OMEGA Library

Pre and Post-condition Computation Variables: x: integer, y: boolean Transition relation: R: x>0 and x´ x-1 and y´ or x<=0 and x´ x and y´ y Set of states: s: x=2 and !y or x=0 and !y Compute post(s, R)

Pre and Post-condition Distribute R: x>0 and x´ x-1 and y´ or x<=0 and x´ x and y´ y s: x=2 and !y or x=0 and y post(s, R) = post(x=2 , x>0 and x´ x-1) post(!y , y´) x=1 y post(x=2 , x<=0 and x´ x) post (!y , y´ y) false !y post(x=0 , x>0 and x´ x-1) post(y , y´) false y post (x=0 , x<=0 and x´ x) post (y, y´ y ) x=0 y = x=1 and y or x=0 and y

Temporal Properties Fixpoints [Emerson and Clarke 80] EF( p) states that can reach p p Pre( p)) . . . p • • • EF( p) Initial states initial states that satisfy EF( p) initial states that violate AG(p) EG( p) states that can avoid reaching p p Pre( p)) . . . • • • EG( p) Initial states initial states that satisfy EG( p) initial states that violate AF(p)

Polymorphic Verifier Symbolic Tran. Sys: : check(Node *f) { • • • Symbolic s = check(f. left) case EX: s. pre(trans. Relation) case EF: do sold = s s. pre(trans. Relation) s. union(sold) while not sold. is. Equal(s) • • • } Action Language Verifier is polymorphic It becomes a BDD based model checker when there or no integer variables

Fixpoints May Not Converge • Integer variables can increase without a bound – state space is infinite • Model checking is undecidable for systems with unbounded integer variables • We use conservative approximations

Conservative Approximations • Compute a lower ( p ) or an upper ( p+ ) approximation to the truth set of the property ( p ) • Action Language Verifier can give three answers: I p 1) “The property is satisfied” sates which violate the property I p p 3) “I don’t know” p p+ p 2) “The property is false and here is a counter-example”

Conservative Approximations • Truncated fixpoint computations – To compute a lower bound for a least-fixpoint computation – Stop after a fixed number of iterations • Widening – To compute an upper bound for the least-fixpoint computation – We use a generalization of the polyhedra widening operator by [Cousot and Halbwachs POPL’ 77]

Widening • Widening operation with composite representation: – Given two composite atoms c 1 and c 2 in consecutive fixpoint iterates, assume that c 1 = b 1 i 1 c 2 = b 2 i 2 where b 1 = b 2 and i 1 i 2 Assume that i 1 is a single polyhedron and i 2 is also a single polyhedron We find pairs of composite atoms which satisfy this criteria

Widening • Assuming that i 1 and i 2 are conjunctions of atomic constraints (i. e. , polyhedra), then i 1 i 2 is defined as: all the constraints in i 1 which are also satisfied by i 2 Example: i 1 = 0 count 2 i 2 = 0 count 3 i 1 i 2 = 0 count This constraint is not satisfied by i 2 so we drop it • Replace i 2 with i 1 i 2 in c 2 • This generates an upper approximation for the least fixpoint computation

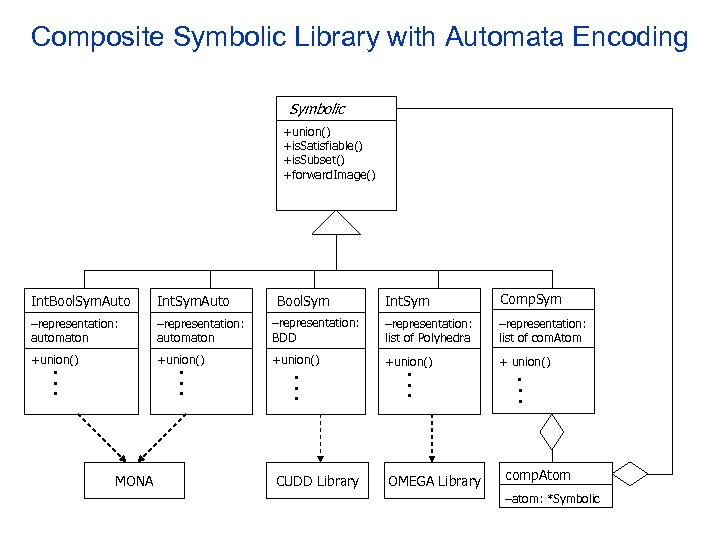Composite Symbolic Library with Automata Encoding Symbolic +union() +is. Satisfiable() +is. Subset() +forward. Image() Int. Bool. Sym. Auto Int. Sym. Auto –representation: automaton +union() • • • MONA Int. Sym Comp. Sym –representation: BDD –representation: list of Polyhedra –representation: list of com. Atom +union() + union() • • • Bool. Sym CUDD Library OMEGA Library • • • comp. Atom –atom: *Symbolic

Automata Representation for Arithmetic Constraints [Bartzis, Bultan CIAA’ 02, IJFCS ’ 02] • Given an atomic linear arithmetic constraint in one of the following two forms we construct an FA which accepts all the solutions to the given constraint • By combining such automata one can handle full Presburger arithmetic

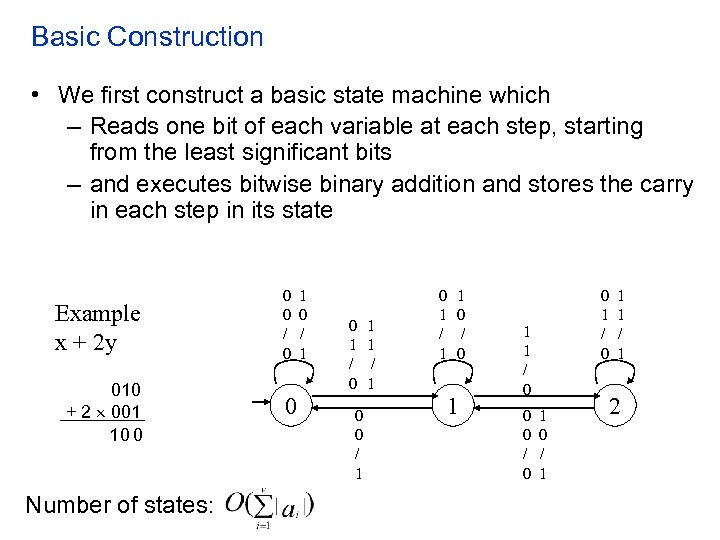Basic Construction • We first construct a basic state machine which – Reads one bit of each variable at each step, starting from the least significant bits – and executes bitwise binary addition and stores the carry in each step in its state Example x + 2 y 010 + 2 001 10 0 Number of states: 0 0 / 0 0 1 0 / 1 0 1 / 0 0 0 / 1 1 1 / 1 0 1 / 1 1 0 / 0 1 1 / 0 0 0 / 0 1 0 / 1 1 1 / 1 2

Automaton Construction • Equality With 0 – All transitions writing 1 go to a sink state – State labeled 0 is the only accepting state – For disequations ( ), state labeled 0 is the only rejecting state • Inequality (<0) – States with negative carries are accepting – No sink state • Non-zero Constant Term c – Same as before, but now -c is the initial state – If there is no such state, create one (and possibly some intermediate states which can increase the size by |c|)

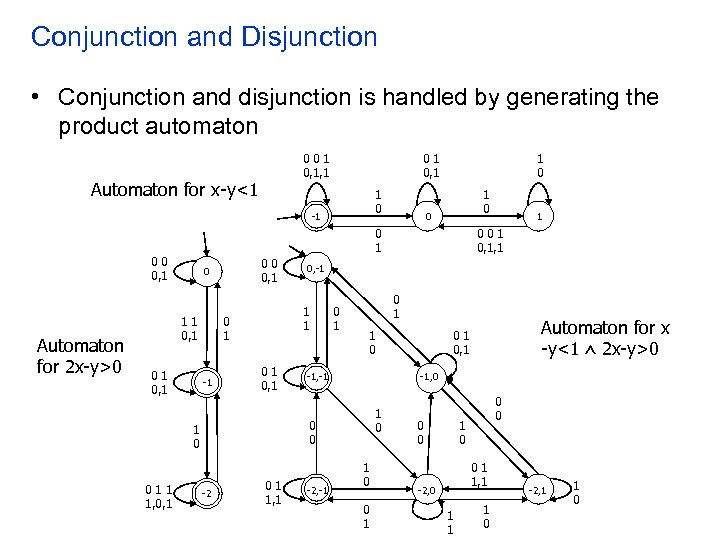Conjunction and Disjunction • Conjunction and disjunction is handled by generating the product automaton 001 0, 1, 1 Automaton for x-y<1 01 0, 1 1 0 -1 00 0, 1 0 11 0, 1 0 0 1 -1 01 0, 1 01 1, 1 001 0, 1, 1 0 1 1 0 -1, -1 -2, -1 Automaton for x -y<1 2 x-y>0 01 0, 1 -1, 0 1 0 0 0 -2 1 0, -1 1 0 011 1, 0, 1 1 0 0 1 00 0, 1 Automaton for 2 x-y>0 1 0 0 1 0 01 1, 1 -2, 0 1 1 1 0 -2, 1 1 0

Other Extensions • Existential quantification (necessary for pre and post) – Project the quantified variables away – The resulting FA is non-deterministic • Determinization may result in exponential blowup of the FA size but we do not observe this in practice – For universal quantification use negation • Constraints on all integers – Use 2’s complement arithmetic – The basic construction is the same – In the worst case the size doubles

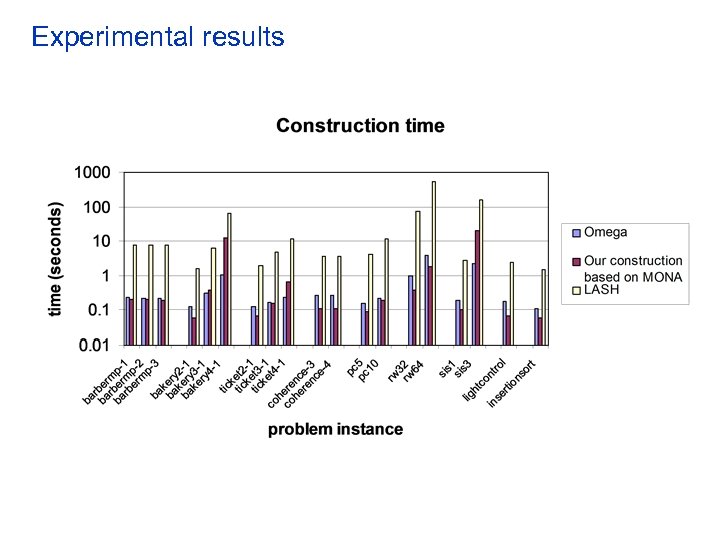
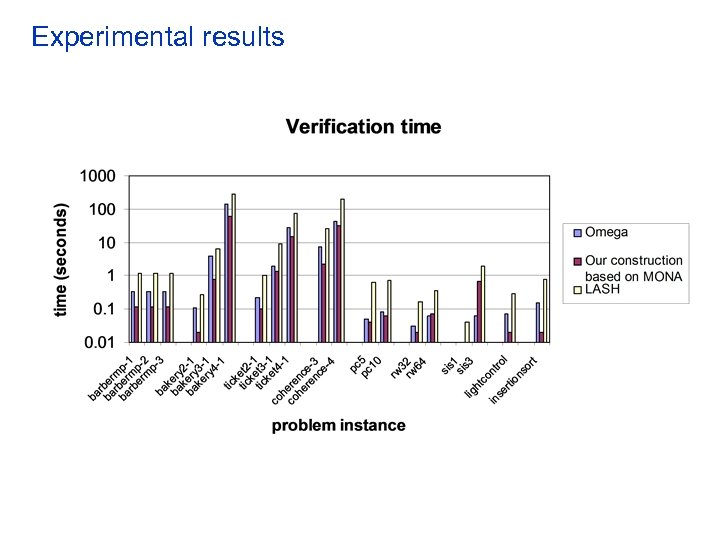
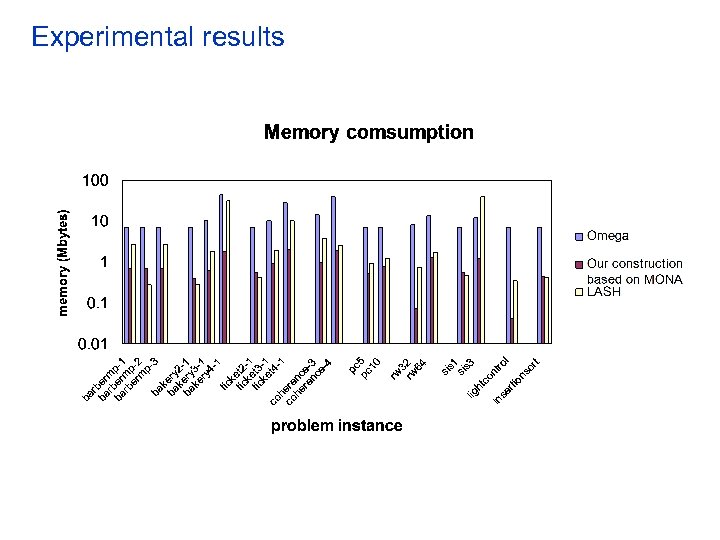
Experiments • We implemented these algorithms using MONA [Klarlund et al] • Integrated them to the Action Language Verifier • We verified a large number of specification examples • We compared our representation against – the polyhedral representation used in the Omega library – the automata representation used in LASH • we also integrated LASH to the Composite Symbolic Library using a wrapper around it

Experimental results

Efficient Pre- and Post-condition Computations [Bartzis, Bultan CAV’ 03] • Pre and post condition computations can cause an exponential blow-up in the size of the automaton in the worst case • We do not observe this blow-up in the experiments • We proved that for a common class of systems this blow up does not occur

Assumptions About the Transition Relation • We assume that the transition relation of the input system is a disjunction of formulas in the following form guard(R) update(R) where – guard(R) is a Presburger formula on current state variables and – update(R) is of the form xi’=f(x 1, …, xv) • j i xj’= xj In asynchronous concurrent systems the transition relation is usually in the above form

Three Classes of Updates 1. xi’ = c 2. xi’ = xi + c 3. xi’ = v j=1 aj· xj + c We proved that • Computation of pre is polynomial for all 3 cases • Computation of post is polynomial for 2 and for 3, whenever ai is odd.

Other Results Related to Automata Encoding [Bartzis, Bultan TACAS’ 03, STTT, CAV’ 04] • We developed efficient algorithms for BDD construction for bounded linear arithmetic constraints – We showed that all three versions of SMV (Nu. SMV, CMU SMV and Cadence SMV) are inefficient in handling linear arithmetic constraints • We defined a widening operator for the automata representation of arithmetic constraints – We can prove that for some cases this widening operator computes the exact fixpoint (for example for updates of the form x’=x+c)

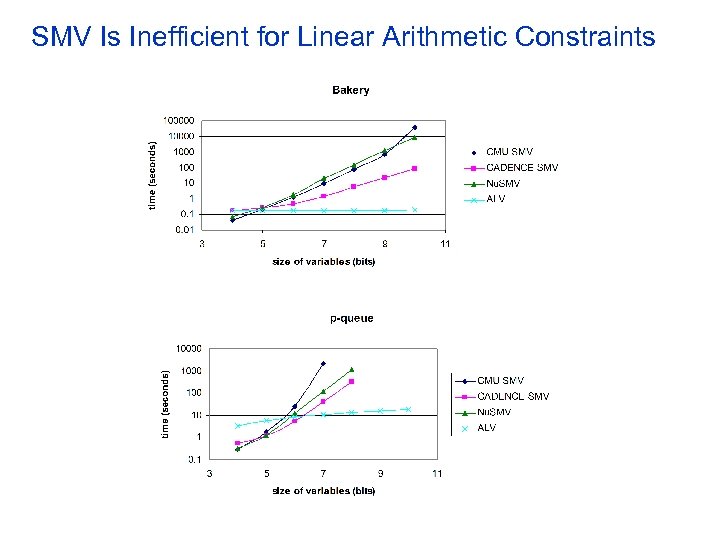SMV Is Inefficient for Linear Arithmetic Constraints

Application to Concurrency Controllers [Yavuz-Kahveci, Bultan ISTTA 02] Outline of our approach: 1. Specify concurrency controllers and concurrent linked lists in Action Language 2. Verify their properties using composite model checking 3. Generate optimized Java classes from the specifications which preserve their properties

Readers-Writers Controller module main() integer nr; boolean busy; restrict: nr>=0; initial: nr=0 and !busy; module Reader() boolean reading; initial: !reading; r. Enter: !reading and !busy and nr’=nr+1 and reading’; r. Exit: reading and !reading’ and nr’=nr-1; Reader: r. Enter | r. Exit; endmodule Writer() boolean writing; initial: !writing; w. Enter: !writing and nr=0 and !busy and busy’ and writing’; w. Exit: writing and !writing’ and !busy’; Writer: w. Enter | w. Exit; endmodule main: Reader() | Writer(); spec: invariant([busy => nr=0]) endmodule

Arbitrary Number of Threads • Counting abstraction – Create an integer variable for each local state of a thread – Each variable will count the number of threads in a particular state • Local states of the threads have to be finite – Specify only the thread behavior that relates to the correctness of the controller – Shared variables of the controller can be unbounded • Counting abstraction can be automated

Readers-Writers After Counting Abstraction Parameterized constants module main() introduced by the counting integer nr; abstractions boolean busy; parameterized integer num. Reader, num. Writer; restrict: nr>=0 and num. Reader>=0 and num. Writer>=0; initial: nr=0 and !busy; Variables introduced by the module Reader() counting abstractions integer reading. F, reading. T; initial: reading. F=num. Reader and reading. T=0; r. Enter: reading. F>0 and !busy and nr’=nr+1 and reading. F’=reading. F-1 and reading. T’=reading. T+1; r. Exit: reading. T>0 and nr’=nr-1 reading. T’=reading. T-1 and reading. F’=reading. F+1; Reader: r. Enter | r. Exit; endmodule Writer(). . . endmodule main: Reader() | Writer(); spec: invariant([busy => nr=0]) endmodule

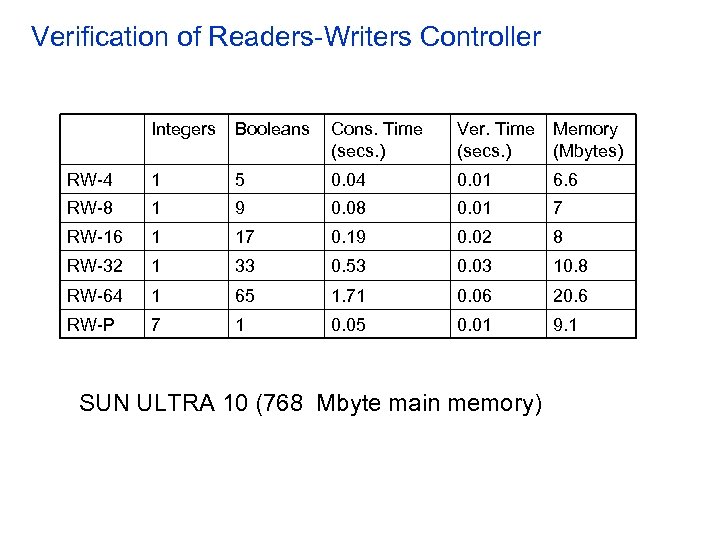Verification of Readers-Writers Controller Integers Booleans Cons. Time (secs. ) Ver. Time (secs. ) Memory (Mbytes) RW-4 1 5 0. 04 0. 01 6. 6 RW-8 1 9 0. 08 0. 01 7 RW-16 1 17 0. 19 0. 02 8 RW-32 1 33 0. 53 0. 03 10. 8 RW-64 1 65 1. 71 0. 06 20. 6 RW-P 7 1 0. 05 0. 01 9. 1 SUN ULTRA 10 (768 Mbyte main memory)

What about the Java Implementation? • We can automatically generate code from the controller specification – Generate a Java class – Make shared variables private variables – Use synchronization to restrict access • Is the generated code efficient? – Yes! – We can synthesize the condition variables automatically – There is no unnecessary thread notification

Specific Notification Pattern [Cargill 96] public class Readers. Writers{ private int nr; private boolean busy; private Object r. Enter. Cond, w. Enter. Cond; private synchronized boolean Guard_r. Enter() { if (!busy) { nr++; return true; } All condition variables and else return false; } wait and signal operations are public void r. Enter() { generated automatically synchronized(r. Enter. Cond) { while(!Guard_r. Enter()) r. Enter. Cond. wait(); } public void r. Exit() { synchronized(this) { nr--; } synchronized(w. Enter. Cond) { w. Enter. Cond. notify(); } }. . . } r. Enter: !reading and !busy and nr’=nr+1 and reading’;

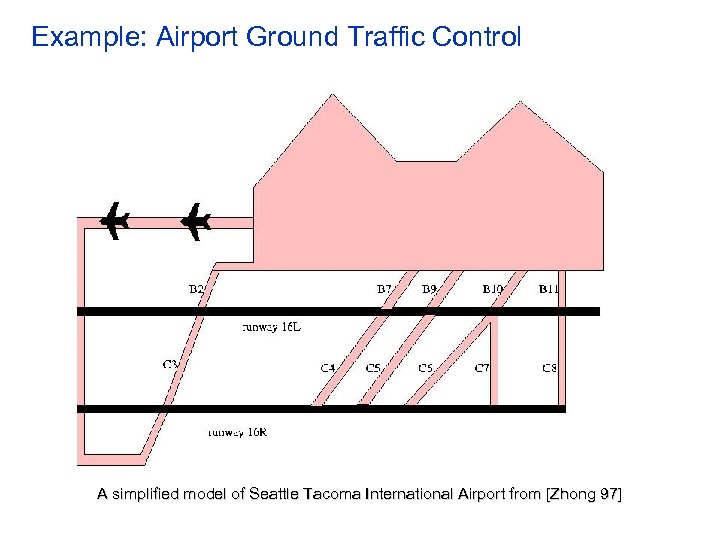Example: Airport Ground Traffic Control A simplified model of Seattle Tacoma International Airport from [Zhong 97]

Action Language Specification module main() integer num. RW 16 R, num. RW 16 L, num. C 3, . . . ; initial: num. RW 16 R=0 and num. RW 16 L=0 and. . . ; module Airplane() enumerated pc {ar. Flow, touch. Down, parked, dep. Flow, taxi. To 16 LC 3, . . . , taxi. Fr 16 LB 2, . . . , takeoff}; initial: pc=ar. Flow or pc=parked; req. Land: pc=ar. Flow and num. RW 16 R=0 and pc’=touch. Down and num. RW 16 R’=num. RW 16 R+1; exit. RW 3: pc =touch. Down and num. C 3=0 and num. C 3’=num. C 3+1 and num. RW 16 R’=num. RW 16 R-1 and pc’=taxi. To 16 LC 3; . . . Airplane: req. Land | exit. RW 3 |. . . ; endmodule main: Air. Plane() | Airplane() |. . ; spec: AG(num. RW 16 R 1 and num. RW 16 L 1) spec: AG(num. C 3 1) spec: AG((num. RW 16 L=0 and num. C 3+num. C 4+. . . +num. C 8>0) => AX(num. RW 16 L=0)) endmodule

Airport Ground Traffic Control • Action Language specification – Has 13 integer variables – Has 6 Boolean variables per airplane process to keep the local state of each airplane – 20 actions • Automatically generated Java monitor class – Has 13 integer variables – Has 14 condition variables – Has 34 methods

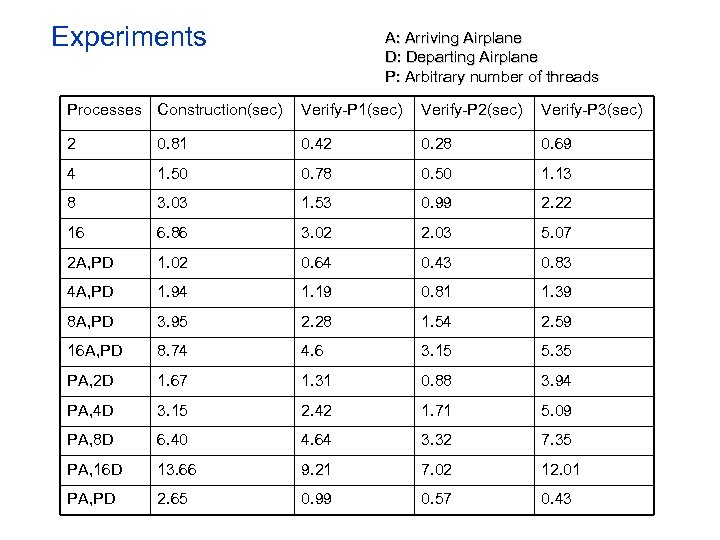Experiments A: Arriving Airplane D: Departing Airplane P: Arbitrary number of threads Processes Construction(sec) Verify-P 1(sec) Verify-P 2(sec) Verify-P 3(sec) 2 0. 81 0. 42 0. 28 0. 69 4 1. 50 0. 78 0. 50 1. 13 8 3. 03 1. 53 0. 99 2. 22 16 6. 86 3. 02 2. 03 5. 07 2 A, PD 1. 02 0. 64 0. 43 0. 83 4 A, PD 1. 94 1. 19 0. 81 1. 39 8 A, PD 3. 95 2. 28 1. 54 2. 59 16 A, PD 8. 74 4. 6 3. 15 5. 35 PA, 2 D 1. 67 1. 31 0. 88 3. 94 PA, 4 D 3. 15 2. 42 1. 71 5. 09 PA, 8 D 6. 40 4. 64 3. 32 7. 35 PA, 16 D 13. 66 9. 21 7. 02 12. 01 PA, PD 2. 65 0. 99 0. 57 0. 43

Efficient Java Implementation public class airport { private int num. RW 16 R; private int num. RW 16 L; private int num. C 3; . . private Object Condreq. Land; private Object Condexit. RW 3; . . . public airport() { num. RW 16 R = 0 ; num. RW 16 L = 0 ; . . . } private synchronized boolean Guarded_req. Land(){ if(num. RW 16 R == 0) { num. RW 16 R = num. RW 16 R + 1; return true; }else return false ; } public void req. Land(){ synchronized(Condreq. Land){ while (! Guarded_req. Land()){ try{ Condreq. Land. wait(); } catch(Interrupted. Exception e){; } }

Heap Type [Yavuz-Kahveci, Bultan SAS 02] • Heap type in Action Language heap {next} top; • Heap type represents dynamically allocated storage top’=new; • We need to add a symbolic representation for the heap type to the Composite Symbolic Library num. Items > 2 => top. next != null

Concurrent Stack module main() heap {next} top, add, get, new. Top; boolean mutex; integer num. Items; initial: top=null and mutex and num. Items=0; module push() enumerated pc {l 1, l 2, l 3, l 4}; initial: pc=l 1 and add=null; push 1: pc=l 1 and mutex and !mutex’ and add’=new and pc’=l 2; push 2: pc=l 2 and num. Items=0 and top’=add and num. Items’=1 and pc’=l 3; push 3: pc=l 3 and top’. next =null and mutex’ and pc’=l 1; push 4: pc=l 2 and num. Items!=0 and add’. next=top and pc’=l 4; push 5: pc=l 4 and top’=add and num. Items’=num. Items+1 and mutex’ and pc’=l 1; push: push 1 | push 2 | push 3 | push 4 | push 5; endmodule pop(). . . endmodule main: pop() | push() ; spec: AG(mutex =>(num. Items=0 <=> top=null)) spec: AG(mutex => (num. Items>2 => top->next!=null)) endmodule

Shape Graphs • Shape graphs represent the states of the heap add heap variables add and top point to node n 1 top n 1 next n 2 next add. next is node n 2 top. next is also node n 2 add. next is null • Each node in the shape graph represents a dynamically allocated memory location • Heap variables point to nodes of the shape graph • The edges between the nodes show the locations pointed by the fields of the nodes

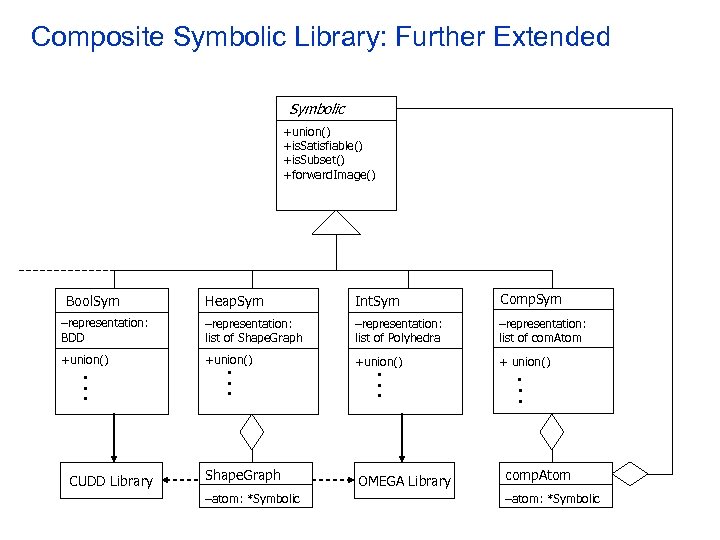Composite Symbolic Library: Further Extended Symbolic +union() +is. Satisfiable() +is. Subset() +forward. Image() Heap. Sym Int. Sym Comp. Sym –representation: BDD –representation: list of Shape. Graph –representation: list of Polyhedra –representation: list of com. Atom +union() + union() Bool. Sym • • • CUDD Library • • • Shape. Graph –atom: *Symbolic • • • OMEGA Library • • • comp. Atom –atom: *Symbolic

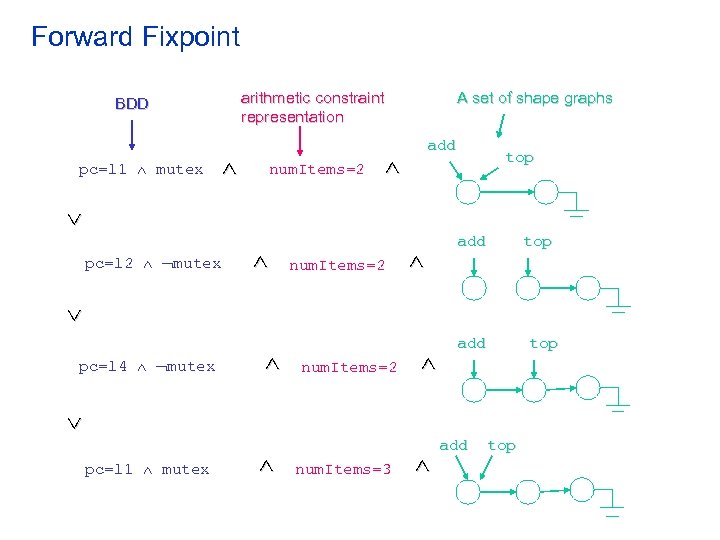Forward Fixpoint arithmetic constraint representation BDD pc=l 1 mutex num. Items=2 A set of shape graphs add top pc=l 2 mutex num. Items=2 add top pc=l 4 mutex num. Items=2 add top pc=l 1 mutex num. Items=3 add top

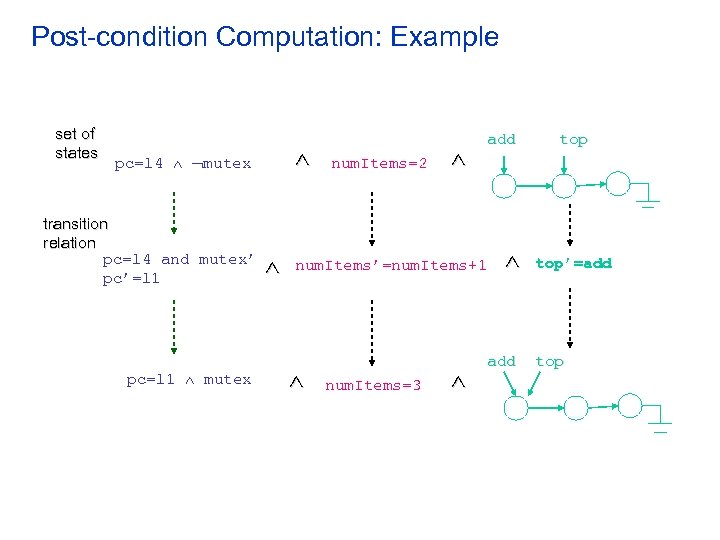Post-condition Computation: Example set of states pc=l 4 mutex transition relation pc=l 4 and mutex’ pc’=l 1 pc=l 1 mutex num. Items=2 add num. Items’=num. Items+1 num. Items=3 add top’=add top

Again: Fixpoints Do Not Converge • We have two reasons for non-termination – integer variables can increase without a bound – the number of nodes in the shape graphs can increase without a bound • As I mentioned earlier, we use widening on integer variables to achieve convergence • For heap variables we use the summarization operation

Summarization • The nodes that form a chain are mapped to a summary node • No heap variable points to any concrete node that is mapped to a summary node • Each concrete node mapped to a summary node is only pointed by a concrete node which is also mapped to the same summary node • During summarization, we also introduce an integer variable which counts the number of concrete nodes mapped to a summary node

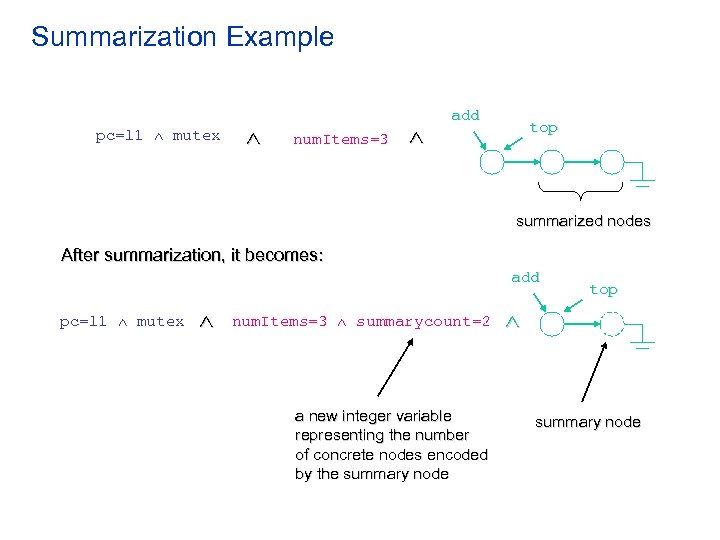Summarization Example pc=l 1 mutex num. Items=3 add top summarized nodes After summarization, it becomes: add pc=l 1 mutex num. Items=3 summarycount=2 a new integer variable representing the number of concrete nodes encoded by the summary node top summary node

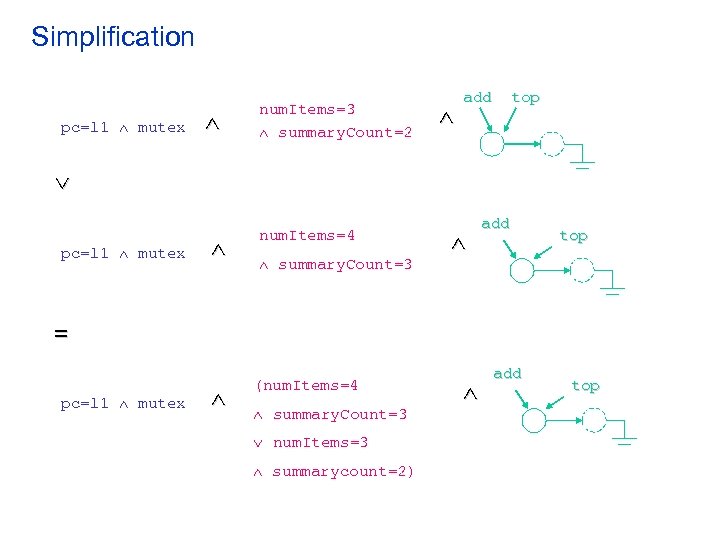Simplification pc=l 1 mutex num. Items=3 summary. Count=2 add top pc=l 1 mutex num. Items=4 (num. Items=4 summary. Count=3 add top = pc=l 1 mutex summary. Count=3 num. Items=3 summarycount=2) add top

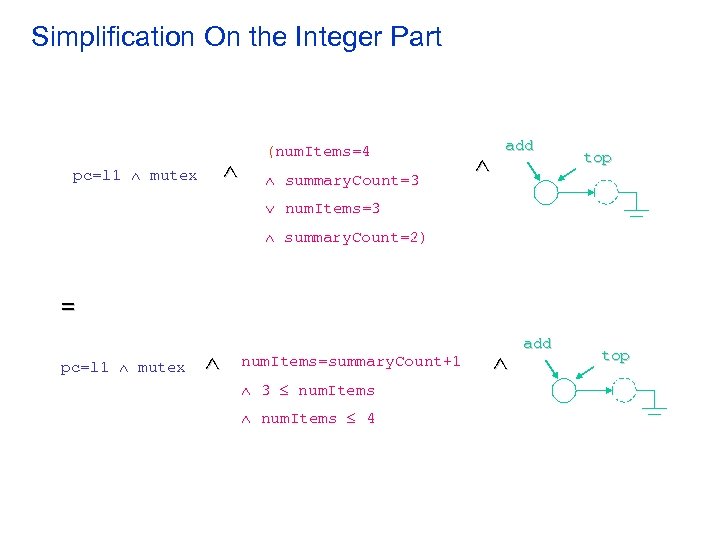Simplification On the Integer Part pc=l 1 mutex (num. Items=4 summary. Count=3 add top num. Items=3 summary. Count=2) = pc=l 1 mutex num. Items=summary. Count+1 3 num. Items 4 add top

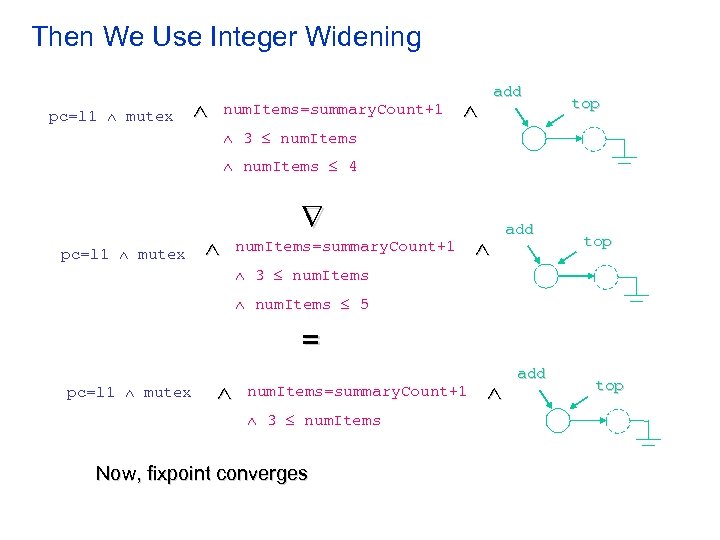Then We Use Integer Widening pc=l 1 mutex num. Items=summary. Count+1 add top 3 num. Items 4 pc=l 1 mutex num. Items=summary. Count+1 add top 3 num. Items 5 = pc=l 1 mutex num. Items=summary. Count+1 3 num. Items Now, fixpoint converges add top

Verified Properties Specification Verified Invariants Stack top=null num. Items=0 top null num. Items 0 num. Items=2 top. next null Single Lock Queue head=null num. Items=0 head null num. Items 0 (head=tail head null) num. Items=1 head tail num. Items 0 Two Lock Queue num. Items>1 head tail num. Items>2 head. next tail

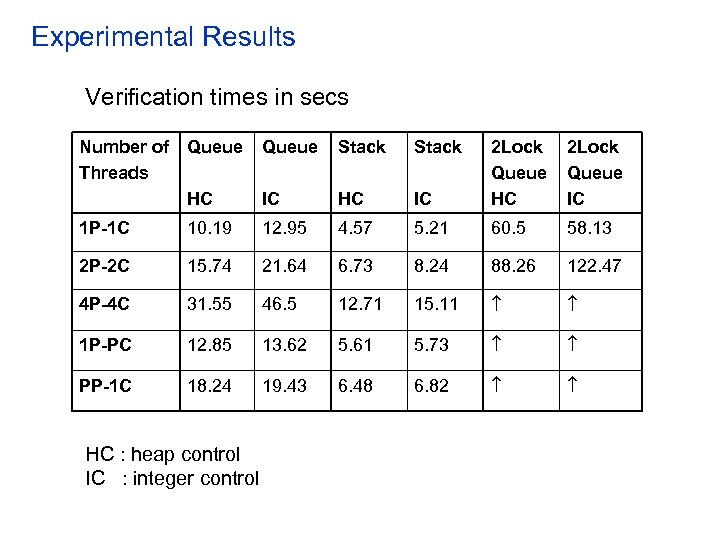Experimental Results Verification times in secs Number of Threads Queue Stack IC 2 Lock Queue HC 2 Lock Queue IC HC 1 P-1 C 10. 19 12. 95 4. 57 5. 21 60. 5 58. 13 2 P-2 C 15. 74 21. 64 6. 73 8. 24 88. 26 122. 47 4 P-4 C 31. 55 46. 5 12. 71 15. 11 1 P-PC 12. 85 13. 62 5. 61 5. 73 PP-1 C 18. 24 19. 43 6. 48 6. 82 HC : heap control IC : integer control

Verifying Linked Lists with Multiple Fields • Pattern-based summarization – User provides a graph grammar rule to describe the summarization pattern L x = next x y, prev y x, L y • Represent any maximal sub-graph that matches the pattern with a summary node – no node in the sub-graph pointed by a heap variable

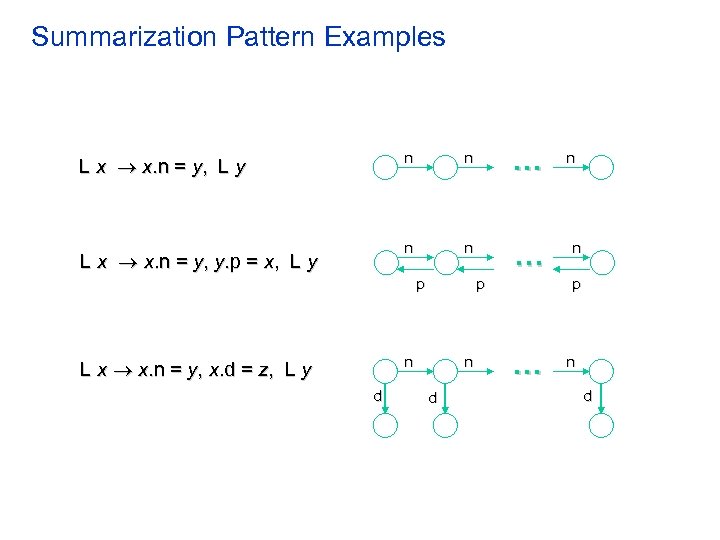Summarization Pattern Examples n L x x. n = y, y. p = x, L y n . . . n L x x. n = y, L y n . . . p p n L x x. n = y, x. d = z, L y d n d . . . n n p n d

Shape Analysis • [Sagiv, Reps, Wilhelm TOPLAS’ 98] , [Dor, Rodeh, Sagiv SAS’ 00] – These papers on shape analysis directly influenced us • [Yahav POPL’ 01] – Verification of concurrent linked lists with arbitrary number of processes • [Sagiv, Reps, Wilhelm TOPLAS], [Lev-Ami, Reps, Sagiv, Wilhelm ISSTA 00] – 3 -valued logic and instrumentation predicates • [Sagiv, Reps, Wilhelm ESOP 03] – Automatically generating instrumentation predicates • [Deutch PLDI’ 94] – Deutch used integer constraint lattices to compute aliasing information using symbolic access paths • [Fradet and Metayer POPL 97] – The idea of summarization patterns is based on the shape types introduced in the above paper

Model Checking Software Specifications • [Atlee, Gannon 93] – Translating SCR mode transition tables to input language of explicit state model checker EMC [Clarke, Emerson, Sistla 86] • [Chan et al. 98, 00] – Translating RSML specifications to input language of SMV • [Bharadwaj, Heitmeyer 99] – Translating SCR specifications to Promela, input language of automata-theoretic explicit state model checker SPIN

Specification Languages • Specification languages for verification – [Milner 80] CCS – [Chandy and Misra 88] Unity – [Lamport 94] Temporal Logic of Actions (TLA) • Specification languages for model checking – [Holzmann 98] Promela – [Mc. Millan 93] SMV – [Alur and Henzinger 96, 99] Reactive Modules

Action Language TLA Connection • Similarities: – Transition relation is defined using predicates on current (unprimed) and next state (primed) variables – Each predicate is defined using integer arithmetic, boolean logic, etc. • Differences: In Action Language – Temporal operators are not used in defining the transition relation • Dual language approach: temporal properties (in CTL) are redundant, they are used to check correctness – Synchronous and asynchronous composition operators are not equivalent to logical operators

Constraint-Based Verification • [Cooper 71] – Used a decision procedure for Presburger arithmetic to verify sequential programs represented in a block form • [Cousot and Halbwachs 78] – Used real arithmetic constraints to discover invariants of sequential programs • [Halbwachs 93] – Constraint based delay analysis in synchronous programs • [Halbwachs et al. 94] – Verification of linear hybrid systems using constraint representations • [Alur et al. 96] – Hy. Tech, a model checker for hybrid systems • [Delzanno and Podelski 99] – Built a model checker using constraint logic programming framework

Automata-Based Representations • [Klarlund et al. ] – MONA, an automata manipulation tool for verification • [Boudet and Comon CAAP ’ 96] – Translating linear arithmetic constraints to automata • [Wolper and Boigelot TACAS ‘ 00] – verification using automata as a symbolic representation • [Kukula et al. 98] – application of automata based verification to hardware verification • [Bouajjani et al CAV ’ 00] – Regular Model Checking • [Dams, Lakhnech and Steffen CAV ’ 01], [Boigelot, Legay and Wolper CAV ’ 03] – Iterating transducers

Combining Symbolic Representations • [Chan et al. CAV’ 97] – both linear and non-linear constraints are mapped to BDDs – Only data-memoryless and data-invariant transitions are supported • [Bharadwaj and Sims TACAS’ 00] – Combines automata based representations (for linear arithmetic constraints) with BDDs – Specialized for inductive invariant checking • [Bensalem et al. 00] – Symbolic Analysis Laboratory – Designed a specification language that allows integration of different verification tools

Model Checking Programs • Verisoft from Bell Labs [Godefroid POPL 97] – C programs, handles concurrency, bounded search, bounded recursion, stateless search • Java Path Finder (JPF) at NASA Ames [Havelund, Visser] – Explicit state model checking for Java programs, bounded search, bounded recursion, handles concurrency • SLAM project at Microsoft Research [Ball, Rajamani et al. SPIN 00, PLDI 01] – Symbolic model checking for C programs, unbounded recursion, no concurrency – Uses predicate abstraction [Saidi, Graf 97] and BDDs • BANDERA: A tool for extracting finite state models from programs [Dwyer, Hatcliff et al ICSE 00, 01]

Concurrency Controllers and Interfaces [Betin-Can, Bultan Soft. MC 03, ASE’ 04] • • • Concurrency Controller – Behavior: How do the shared variables change – Interface: In which order are the methods invoked Separate Verification – Behavior verification • Action Language Verifier – Interface verification • Java Path. Finder A modular approach – Build complex concurrency controllers by composing interfaces

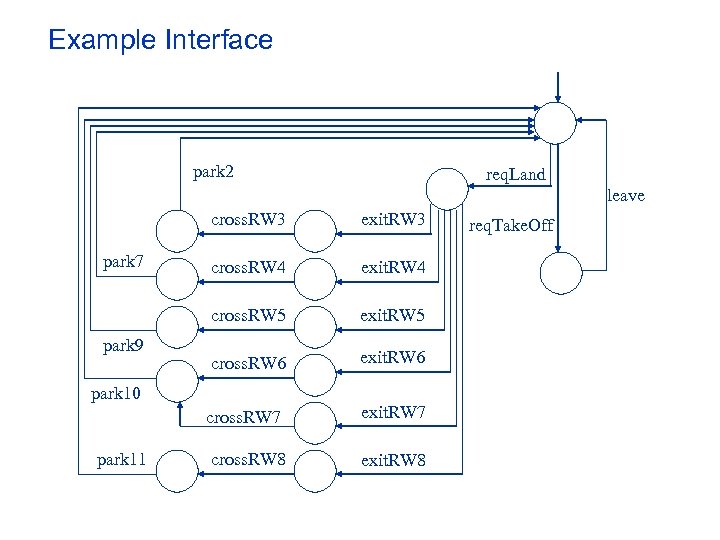Example Interface park 2 req. Land leave cross. RW 3 park 9 cross. RW 4 exit. RW 4 cross. RW 5 park 7 exit. RW 3 exit. RW 5 cross. RW 6 exit. RW 6 park 10 cross. RW 7 park 11 cross. RW 8 exit. RW 7 exit. RW 8 req. Take. Off

Verification of Web Services [Fu, Bultan, Hull, Su TACAS 01, WES 02], [Bultan, Fu, Hull, Su WWW 03], [Fu, Bultan, Su CIAA 03, WWW 04, ISSTA 04, ICWS 04] • Verification of Vortex workflows using SMV and Action Language Verifier • A top-down approach to specification and verification of composite web services – Specify the composite web service as a conversation protocol – Generate peer specifications from the conversation protocol • Realizability conditions • Working on the application of this framework to BPEL – Bottom-up approach using synchronizability analysis

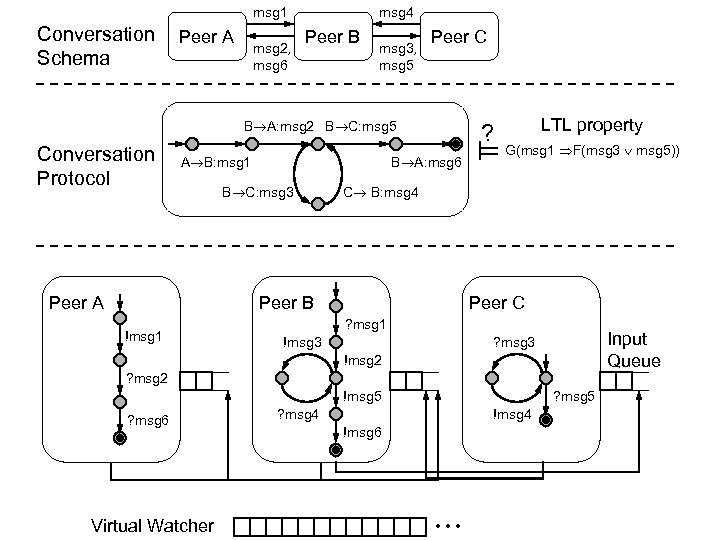msg 1 Conversation Schema Peer A msg 2, msg 6 msg 4 Peer B msg 3, msg 5 Peer C B A: msg 2 B C: msg 5 Conversation Protocol A B: msg 1 Peer A ? B A: msg 6 B C: msg 3 G(msg 1 F(msg 3 msg 5)) C B: msg 4 Peer B !msg 1 LTL property Peer C ? msg 1 !msg 3 Input Queue ? msg 3 !msg 2 ? msg 2 !msg 5 ? msg 6 Virtual Watcher ? msg 5 ? msg 4 !msg 6 . . .

The End The End