ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ТПУ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ПМ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (ТПУ) КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ (ПМ) ИНФОРМАТИКА Лектор: к. т. н. , доцент кафедры ПМ, Зимин Вячеслав Прокопьевич Лабораторные занятия ведут: старший преподаватель кафедры ПМ, Моисеенко Нина Борисовна к. т. н. , доцент кафедры ПМ, Зимин Вячеслав Прокопьевич 1

Тема ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Число – это некоторая абстрактная сущность для описания количества чего-либо. Цифры – это знаки, используемые для записи чисел. Примеры различных цифр: Арабские цифры: 0 1 2 3 4 5 6 7 8 9 Римские цифры: I II III V X L C M 2

Способы записи ЧИСЕЛ можно классифицировать следующим образом: 1) ПОЗИЦИОННЫЕ системы счисления; 2) СМЕШАННЫЕ системы счисления; 3) НЕПОЗИЦИОННЫЕ системы счисления. Примеры СМЕШАННОЙ системы счисления – денежные знаки: - копейки, рубли; - центы, доллары - и т. д. Пример НЕПОЗИЦИОННОЙ системы счисления – обозначение чисел римскими цифрами, I, III, IV, IX, XI, XX, XL, XC, MMX и т. д. 3

ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Наибольшее распространение получили позиционные системы счисления, вследствие удобства их использования при выполнении арифметических операций. Среди позиционных систем счисления человек наиболее часто использует десятичную систему (система по основанию 10). Это такая система, в которой составление чисел производится с помощью десяти цифр: 0 1 2 3 4 5 6 7 8 9 Для внутреннего представления информации в ЭВМ используется двоичная система счисления. В основе двоичной системы счисления лежат две цифры: 0 1 Для промежуточного представления чисел (в человеко-машинном интерфейсе) используются восьмеричная и шестнадцатеричная системы счисления В основе восьмеричной системы счисления лежат восемь цифр: 0 1 2 3 4 5 6 7 В основе шестнадцатеричной системы счисления лежат шестнадцать символов (цифр и букв): 0 1 2 3 4 5 6 7 8 9 A B C D E F Например, в основе пятеричной системы счисления лежат пять цифр: 0 1 2 3 4 4

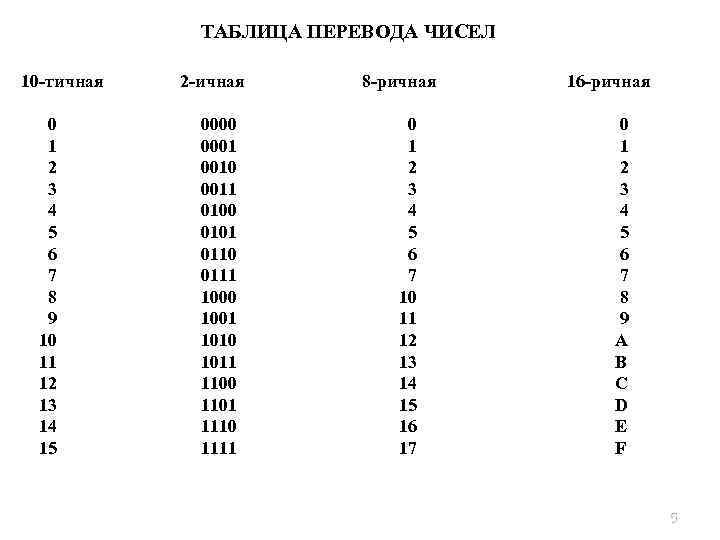ТАБЛИЦА ПЕРЕВОДА ЧИСЕЛ 10 -тичная 2 -ичная 8 -ричная 16 -ричная 0 0000 0 1 0001 1 2 0010 2 3 0011 3 4 0100 4 5 0101 5 6 0110 6 7 0111 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F 5

ОБЩЕЕ ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В общем случае в позиционной системе счисления числа представляются следующим образом: (anan − 1. . . a 0)f , где a 0, a 1, . . . , an - цифры, а f – основание системы счисления. Если используется десятичная система, то основание f – можно опустить. a 0 – это количество единиц в числе; a 1 – это количество десятков в числе; a 2 – это количество сотен в числе; и т. д. Примеры чисел: 110012 – число в двоичной системе счисления, a 0 = 1, a 1 = 0, a 2 = 0, a 3 = 1, a 4 = 1; 2213 – число в троичной системе счисления, a 0 = 1, a 1 = 2, a 2 = 2; 318 – число в восьмеричной системе счисления, a 0 = 1, a 1 = 3; 2510 – число в десятичной системе счисления, a 0 = 5, a 1 = 2; AE 916 – число в шестнадцатеричной системе счисления, a 0 = 9, a 1 = E, a 3 = A. 6

ПРЕДСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ ЧИСЕЛ В общем случае, в позиционной системе с любым основание целое число можно представить следующим образом: (anan − 1. . . a 0)f = an·fn +. . . + a 1 · f 1 + a 0 · f 0, где a 0, a 1, . . . , an – цифры, а f – основание системы счисления. a 0 – младший разряд числа; / : * ? « < > | an – старший разряд числа. Примеры: Посмотрим чему равны числа в различных системах счисления при переводе их в десятичную систему счисления. Используем только что приведённую формулу: 110012 = 1 · 24 + 1 · 23 + 0 · 22 + 0 · 21 + 1 · 20 = 16 + 8 + 1 = 2510; 318 = 3 · 81 + 1 · 80 = 24 + 1 = 2510; 1916 = 1 · 161 + 9 · 160 = 16 + 9 = 2510. 7

ПРАВИЛА ПЕРЕВОДА ЦЕЛЫХ ЧИСЕЛ Перевод из десятичной системы счисления в двоичную и шестнадцатеричную 1) исходное целое число делится на основание системы счисления, в которую переводится (на 2 – при переводе в двоичную систему счисления или на 16 – при переводе в шестнадцатеричную); получается частное и остаток; 2) если полученное частное меньше основания системы счисления, в которую выполняется перевод, процесс деления прекращается, переходят к шагу 3. Иначе над частным выполняют действия, описанные в шаге 1; 3) все полученные остатки и последнее частное преобразуются в соответствии с таблицей перевода чисел в цифры (символы) той системы счисления, в которую выполняется перевод; 4) формируется результирующее число: его старший разряд – полученное последнее частное, каждый последующий младший разряд образуется из полученных остатков от деления, начиная с последнего и кончая первым. Таким образом, младший разряд полученного числа – первый остаток от деления, а старший – последнее частное. 8

ПРАВИЛА ПЕРЕВОДА ЦЕЛЫХ ЧИСЕЛ Перевод из двоичной и шестнадцатеричной систем счисления в десятичную В этом случае рассчитывается полное значение числа по формуле (anan − 1. . . a 0)f = an·fn +. . . + a 1 · f 1 + a 0 · f 0 = (число в 10 -ой системе), где an, an − 1, . . . , a 0 – цифры, а f – основание исходной системы счисления. Перевод из двоичной системы счисления в шестнадцатеричную 1) исходное число разбивается на тетрады (т. е. 4 цифры), начиная с младших разрядов. Если количество цифр исходного двоичного числа не кратно 4, оно дополняется слева незначащими нулями до достижения кратности 4; 2) каждая тетрада заменятся соответствующим шестнадцатеричным символом в соответствии с таблицей перевода чисел. Перевод из шестнадцатеричной системы счисления в двоичную 1) Каждый шестнадцатеричный символ исходного числа заменяется тетрадой двоичных цифр в соответствии с таблицей перевода чисел. Если в таблице двоичное число имеет менее 4 цифр, оно дополняется слева незначащими нулями до тетрады; 9 2) незначащие нули в результирующем числе отбрасываются.

ПРЕДСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ ЧИСЕЛ Примеры: 1) Возьмём для примера число 2510 и получим представление этого числа в двоичной системе счисления: 25 / 2 = 12, остаток 1; 12 / 2 = 6, остаток 0; 6 / 2 = 3, остаток 0; 3 / 2 = 1, остаток 1; 1 / 2 = 0, остаток 1. Записываем в обратном порядке. Получили число: 110012. 2) Представим число 2510 в троичной системе счисления: 25 / 3 = 8, остаток 1; 8 / 3 = 2, остаток 2; 2 / 3 = 0, остаток 2. Записываем в обратном порядке. Получили число: 2213. 10

ПРЕДСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ ЧИСЕЛ Примеры: 1) Представим число 2510 в восьмеричной системе счисления: 25 / 8 = 3, остаток 1; Получили число: 318. 2) Представим число 2510 в шестнадцатеричной системе счисления: 25 / 16 = 1, остаток 9. Получили число: 1916. 3) Представим число 2 E 16 в двоичной системе счисления. В соответствии с таблицей перевода чисел отдельно представляет цифры 2 и E в двоичной системе счисления: 216 = 00102 E 16 = 11102, отбрасываем для 2 незначащие нули 216 = 102 и окончательно Получили число: 1011102 11