2f884116569c6e9003cdf07d93c9dace.ppt
- Количество слайдов: 85

Tolerant Retrieval Some of these slides are based on Stanford IR Course slides at http: //www. stanford. edu/class/cs 276/ 1

Tolerant Retrieval • Up until now, we assumed: – Input: Boolean query – Output: Documents precisely satisfying query • How can we allow imprecise querying? (1) Wildcard queries (2) Preprocessing of text and queries (3) Spelling correction 2

Indexing for Wildcard Queries 3

Finding Lexicon Entries • Given a term t, we can find documents containing t using binary search of the lexicon • What happens if t contains a wild card (“*”)? – Wildcards correspond to a series of any length of characters • How can we find documents with the following terms? – lab* – *or – lab*r Easy! Which of these is Harder? 4

Special Purpose Indices • To efficiently support wildcards, we can create special indices: – N-gram Index or – Rotated Lexicon 5

n-grams • n-grams are sequences of n letters in a word – digram = 2 -gram • use $ to mark beginning and end of word • Example: Digrams of labor are: – $l, la, ab, bo, or, r$ • Given a word with k letters (not including surrounding $ symbols), how many digrams will the word have? – How many n-grams? 6

n-grams Index • Create an index that stores, for each n-gram, the list of terms containing that n-gram – So, for digram he, we would have the list containing the terms he, hello, help, she, the, … • To save space, instead of storing the terms, we store pointers to entries in the lexicon, i. e. , term numbers – So, for digram he, we would have the list containing the term numbers, e. g. , 7, 8, 10, 117, 232, … 7
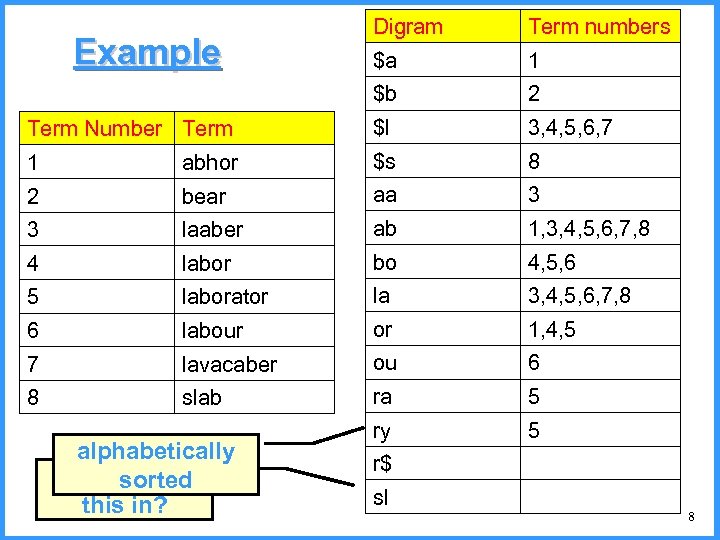
Digram Term numbers $a 1 $b 2 Term Number Term $l 3, 4, 5, 6, 7 1 abhor $s 8 2 bear aa 3 3 laaber ab 1, 3, 4, 5, 6, 7, 8 4 labor bo 4, 5, 6 5 laborator la 3, 4, 5, 6, 7, 8 6 labour or 1, 4, 5 7 lavacaber ou 6 8 slab ra 5 ry 5 r$ sl Example alphabetically Can you fill sorted this in? 8
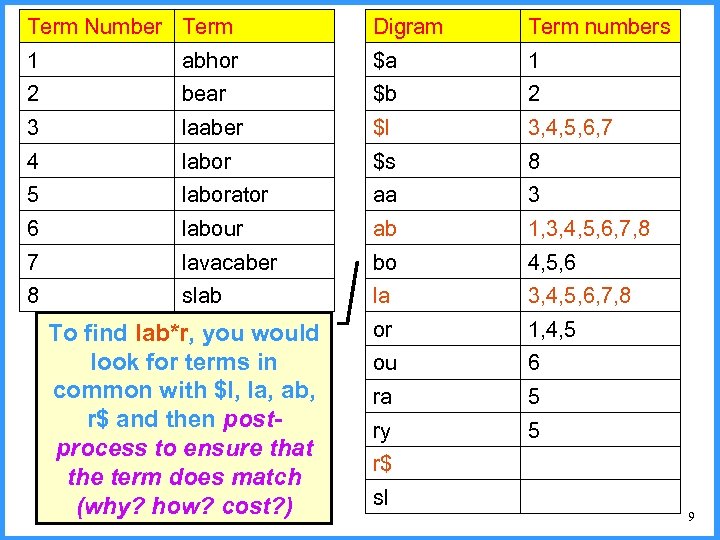
Term Number Term Digram Term numbers 1 abhor $a 1 2 bear $b 2 3 laaber $l 3, 4, 5, 6, 7 4 labor $s 8 5 laborator aa 3 6 labour ab 1, 3, 4, 5, 6, 7, 8 7 lavacaber bo 4, 5, 6 8 slab la 3, 4, 5, 6, 7, 8 or 1, 4, 5 ou 6 ra 5 ry 5 r$ sl To find lab*r, you would look for terms in common with $l, la, ab, r$ and then postprocess to ensure that the term does match (why? how? cost? ) 9

Rotated Terms • If wildcard queries are common, we can save on time at the cost of more space, using a rotated lexicon • Let t = c 1, …, cn be a sequence of characters • Let 1 i n be a number • The i-rotation of t is the sequence of characters ci, …, cn, c 1, …, ci-1 10

Rotated Terms • Given a term t of length n, we use Rot(t) to denote the set of derived by: – Padding t with a starting $ symbol – Taking all i-rotations where 1 i n +1 • How big is Rot(t)? • Example: – What is Rot(labor)? 11

Rotated Lexicons • A rotated lexicon contains, for each term t in the lexicon, and for each rotation t’ of t in Rot(t), an entry of the form (k, i), where – k is the term number of t in the (regular) lexicon – t’ is the i-rotation of t • Note that (k, i) uniquely identifies a rotated term • These entries are stored in alphabetical order of the rotated terms 12
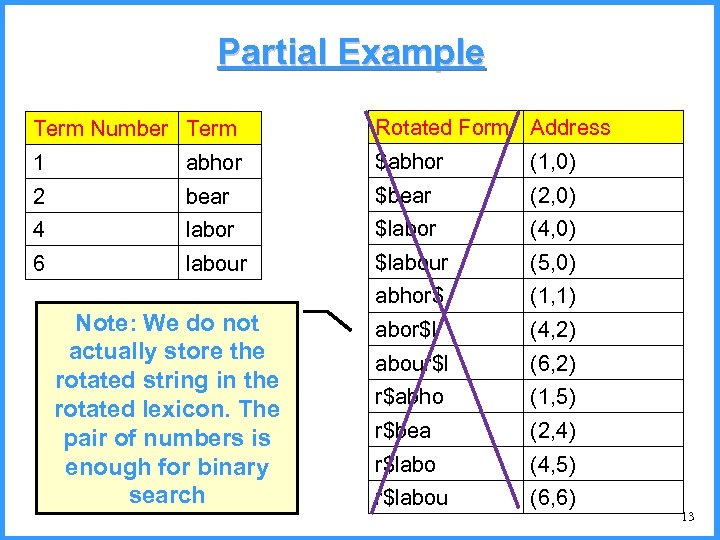
Partial Example Term Number Term Rotated Form Address 1 abhor $abhor (1, 0) 2 bear $bear (2, 0) 4 labor $labor (4, 0) 6 labour $labour (5, 0) abhor$ (1, 1) abor$l (4, 2) abour$l (6, 2) r$abho (1, 5) r$bea (2, 4) r$labo (4, 5) r$labou (6, 6) Note: We do not actually store the rotated string in the rotated lexicon. The pair of numbers is enough for binary search 13
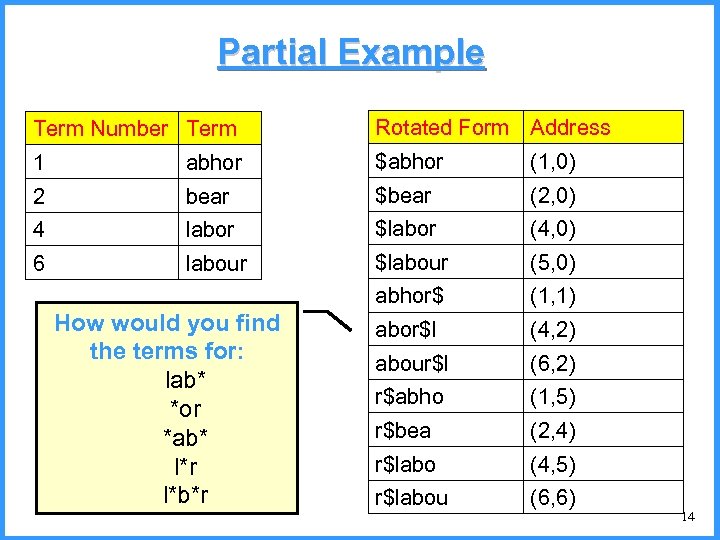
Partial Example Term Number Term Rotated Form Address 1 abhor $abhor (1, 0) 2 bear $bear (2, 0) 4 labor $labor (4, 0) 6 labour $labour (5, 0) abhor$ (1, 1) abor$l (4, 2) abour$l (6, 2) r$abho (1, 5) r$bea (2, 4) r$labo (4, 5) r$labou (6, 6) How would you find the terms for: lab* *or *ab* l*r l*b*r 14

Summary • We now know how to find terms that match a wildcard query • Basic steps for query evaluation for a wildcard query – lookup the wildcard-ed words in an auxiliary index, to find all possible matching terms – given these terms proceed with normal query processing (as if this was not a wildcard query) • But, we have not yet explained how normal query processing should proceed! (later…) 15

Preprocessing Data and Queries 16

Choosing What Data To Store • We would like the user to be able to get as many relevant answers to his query as possible • Examples: – Query: computer science. Should it match Computer Science? – Query: data compression. Should it match compressing data? • The way we store the data in our lexicon will affect our answers to the queries 17
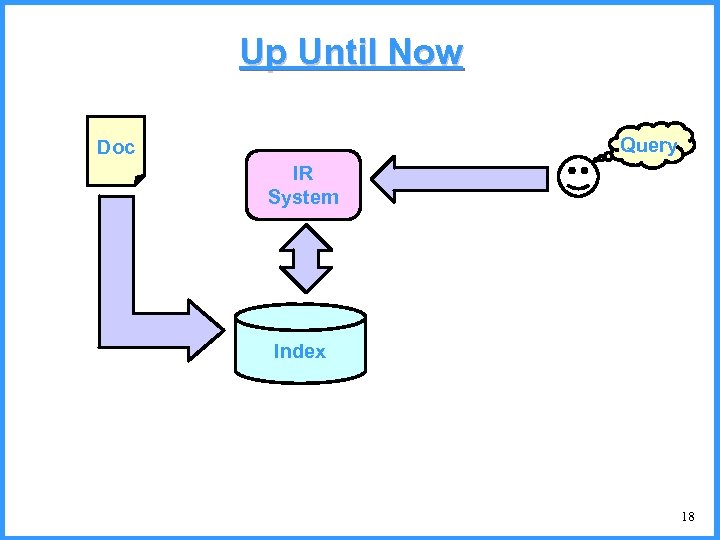
Up Until Now Query Doc IR System Index 18
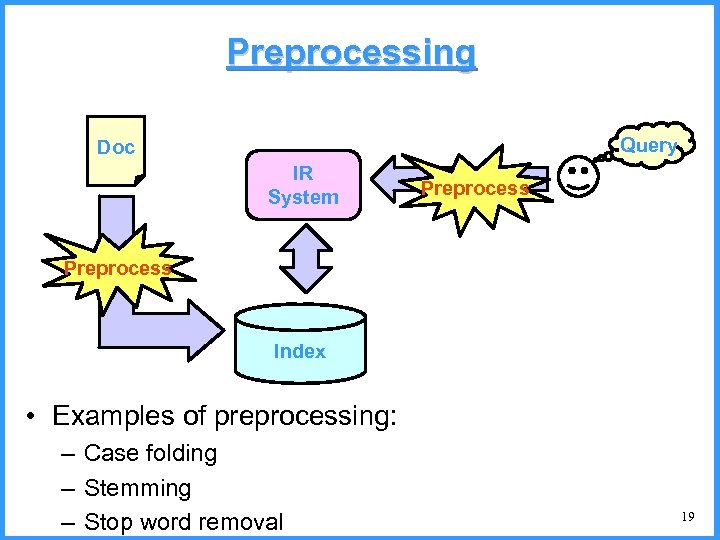
Preprocessing Query Doc IR System Preprocess Index • Examples of preprocessing: – Case folding – Stemming – Stop word removal 19
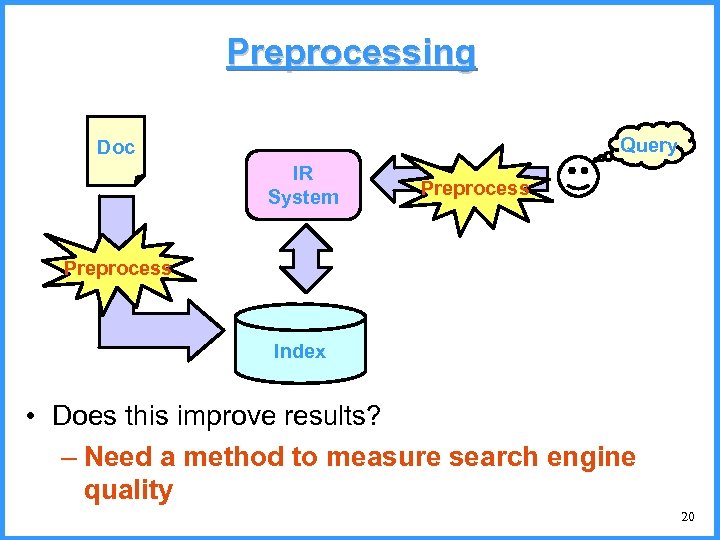
Preprocessing Query Doc IR System Preprocess Index • Does this improve results? – Need a method to measure search engine quality 20

Relevant and Irrelevant • The user has a task, which he formulates as a query • A given document may contain all words and yet not be relevant • A given document may not contain all words and yet be relevant • Relevance is subjective and can only be determined by the user 21

Evaluating the Quality of Search Results • Goals: – Return all relevant documents – Return no non-relevant documents – Return relevant documents “earlier” • Suppose that a search engine runs a query Q and returns the result set R. Then, a document falls in one of the categories: Relevant Not Relevant Retrieved Not Retrieved 22

Quality of Search Results • Standard measures of accuracy – Precision: percentage of retrieved documents that are relevant – Recall: percentage of relevant documents that are retrieved • Other measures discussed later… 23

Case Folding • Normally accepted to perform case folding, i. e. , to reduce all words to lower-case form before storing in the lexicon • User’s query is transformed to lower case before looking for the terms in the index • What affect does this have on the lexicon size? • Does this increase precision? Recall? – Computer Science computer science – Bush bush – SOAP soap 24

Stemming • Suppose that a user is interested in finding pages about “running shoes” – We may also want to return pages with shoe – We may also want to return pages with run or runs • Solution: Use a stemmer – Stemmer returns the stem ( )שורש of the word 25

Porter Stemmer • A multi-step, longest-match stemmer. – Paper introducing this stemmer can be found online • Notation –v vowel(s) =תנועות AEIOU –c consonant(s) עיצורים – (vc)m times vowel(s) followed by consonant(s), repeated m • Any word can be written: [c](vc)m[v] – brackets are optional – m is called the measure of the word • We discuss only the first few rules of the stemmer 26

Porter Stemmer: Step 1 a Follow first applicable rule Suffix Replacement Examples ss caresses => caress ? ies i ? ponies => poni ties => ti ? ss ss caress => caress ? s null cats => cat ? 27
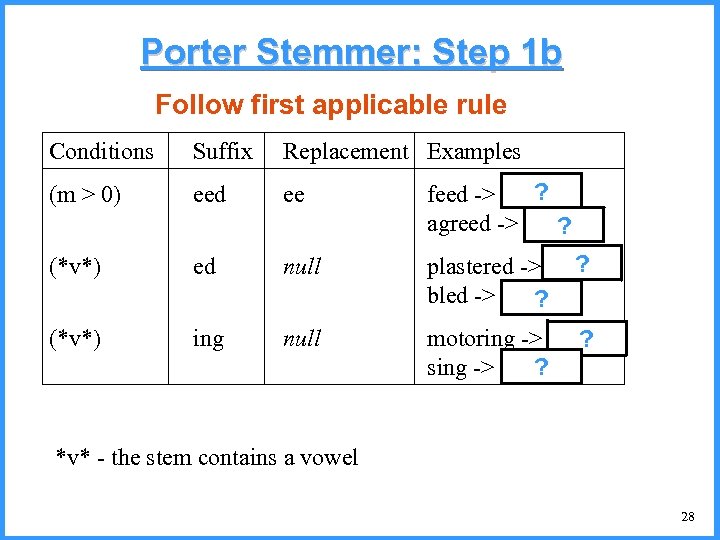
Porter Stemmer: Step 1 b Follow first applicable rule Conditions Suffix Replacement Examples (m > 0) eed ee ? feed -> feed agreed -> agree ? (*v*) ed null ? plastered -> plaster bled -> bled ? (*v*) ing null motoring -> motor ? sing -> sing ? *v* - the stem contains a vowel 28

Stemming Effectiveness • Does stemming improve query results? • Will precision increase / decrease? • Will recall increase / decrease? 29

Stop Words • Stop words are very common words that generally are not of importance, e. g. : the, a, to • Such words take up a lot of room in the index (why? ) • They slow down query processing (why? ) • They generally do not improve the results (why? ) • Some search engines do not store these words at all, and remove them from queries – Is this always a good idea? 30

Spelling correction 31

Spelling Tasks • Spelling Error Detection • Spelling Error Correction: – Autocorrect • hte the – Suggest a correction – Suggestion lists 32

Types of spelling errors • Non-word Errors – graffe giraffe • Real-word Errors – Typographical errors Spelling Errors are Common! 26%: Web queries Wang et al. 2003 • three there – Cognitive Errors (homophones) • piece peace, • too two • your you’re 33

Non-word spelling errors • Non-word spelling error detection: – Any word not in a dictionary is an error – The larger the dictionary the better – (The Web is full of mis-spellings, so the Web isn’t necessarily a great dictionary … but …) • Non-word spelling error correction: – Generate candidates: real words that are similar to error – Choose the one which is best, considering: • Similarity to error word (edit distance) • Likelihood of candidate (noisy channel probability) 34

Real word spelling errors • For each word w, generate candidate set: – Find candidate words with similar pronunciations – Find candidate words with similar spellings – Include w in candidate set • Choose best candidate – Noisy Channel view of spell errors Can also do this for non-word correction – Context-sensitive – so have to consider whether the surrounding words “make sense” – Flying form Heathrow to LAX Flying from Heathrow to LAX 35

Spell Correction • To spell correct, we have to be able to (1) Find syntactically similar words (2) Assess likelihood of a word appearing • We start with (1), by introducing the notion of Edit Distance 36

Finding Similar Words • Problem: Given a lexicon and a character sequence Q, return the words in the lexicon closest to Q • What’s “closest”? • We’ll study several alternatives – Edit distance – Weighted edit distance – n-gram overlap 37

Edit distance • Edit Distance: Given two strings S 1 and S 2, the edit distance of S 1 to S 2 is the minimum number of basic operations to convert one to the other – Insert a Character – Delete a Character – Replace a Character with a different Character – (Transpose adjacent characters: Damerau. Levenshtein Edit Distance, not covered here) 38

Edit Distance Example • What is the edit distance of – cat to dot? – cat to caat? – cat to act? – What is the maximal edit distance between any two strings s and t? • Can be found in polynomial time, using dynamic programming. 39

Computing Edit Distance: Intuition • To compute edit distance of s and t: – Create a matrix d with 0, …, |s| columns and 0, …, |t| rows – The entry d[i, j] is the edit distance between the words: si (i. e. prefix of size i) and tj (i. e. prefix of t of size j) • What will be in d[s 0, t 1]? • What will be in d[s 0, tj]? • What will be in d[si, t 0]? • What will be in d[s|s|, t|t|]? 40

Computing Edit Distance (1) To compute the edit distance of s and t: 1. n : = length(s) m : = length(t) If n = 0, return m and exit. If m = 0, return n and exit. 2. Construct a matrix containing 0. . m rows and 0. . n columns. Initialize the first row to 0. . n. Initialize the first column to 0. . m. 41

Computing Edit Distance (2) 3. for i = 1 to n 4. for j = 1 to m 5. If s[i] = t[j] then cost : = 0. else cost : = 1. 3. d[i, j] : = min(d[i-1, j]+1, d[i, j-1]+1, d[i-1, j-1]+cost) 7. Return d[n, m] 42
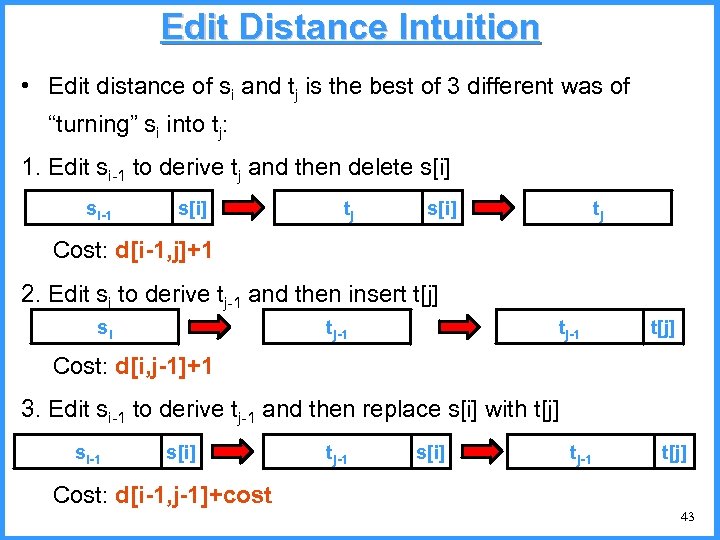
Edit Distance Intuition • Edit distance of si and tj is the best of 3 different was of “turning” si into tj: 1. Edit si-1 to derive tj and then delete s[i] si-1 s[i] tj Cost: d[i-1, j]+1 2. Edit si to derive tj-1 and then insert t[j] si tj-1 t[j] Cost: d[i, j-1]+1 3. Edit si-1 to derive tj-1 and then replace s[i] with t[j] si-1 s[i] tj-1 t[j] Cost: d[i-1, j-1]+cost 43
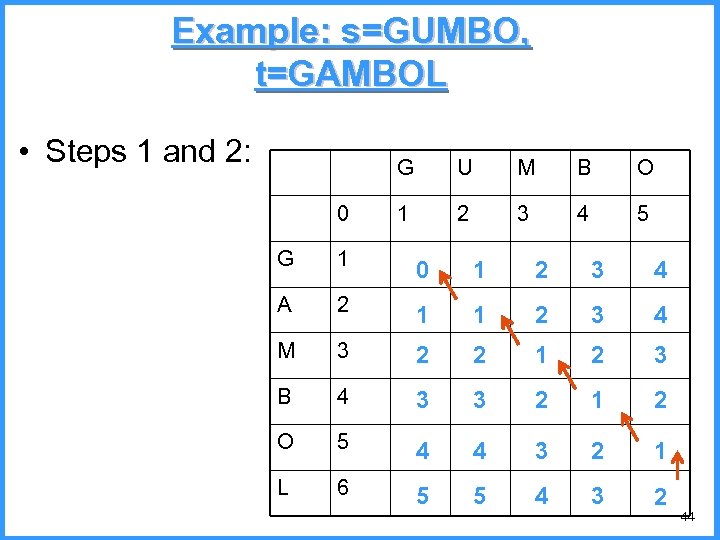
Example: s=GUMBO, t=GAMBOL • Steps 1 and 2: G 0 U M B O 1 2 3 4 5 G 1 0 1 2 3 4 A 2 1 1 2 3 4 M 3 2 2 1 2 3 B 4 3 3 2 1 2 O 5 4 4 3 2 1 L 6 5 5 4 3 2 44

Weighted edit distance • The weighted version of edit distance takes into consideration the characters involved, by giving different weights to different operations – Can capture keyboard errors, e. g. m more likely to be mistyped as n than as q – Can capture common spelling errors, e. g. , c and k are likely to be typed one for another • Require weight matrix as input • Simple modification of dynamic programming to handle weights 45

Using Edit Distance to Find Similar Words • Given a (misspelled) query, how do we find similar, correctly spelled, words? – Edit distance to every word in dictionary? No! expensive and slow – Use special structures to find all words of edit distance 1 or 2 (Good! details omitted, but think about it!) – Use n-gram overlap to find words that are likely to have low edit distance 46

n-gram overlap • Given the misspelled word t, – find all n-grams of t – using the n-gram index, find all words in the lexicon that have n-grams in common with t – Consider as candidates words from the lexicon that are sufficiently similar in their n-grams to t – For these candidates, we will compute the actual edit distance 47

Similar Sets of n-grams • The Jaccard Coefficient is a commonly-used measure of similarity of sets (measures overlap) • Let X and Y be two sets (e. g. , the set of n-grams of two words), the Jaccard Coefficient of X and Y is: • Always between 0 and 1 • Equals 1 when X = Y and 0 when X Y = 48

Example • Misspelled word: Isreal • Lexicon contains: – Israel – real – surreal – really … • Suppose you are using bigrams, and require a Jaccard coefficient of at least 0. 5 • Which words are candidates to check their edit distance, and what are the edit distances derived? 49

So Far… • Given two words, we can assess how similar they are • Given a word, we can find similarly spelled words • However, to spell-check properly, we need to also take into consideration word likelihood (possibly with context) – Coming up next! 50

Spelling Correction and the Noisy Channel 51

Noisy Channel Intuition 52

Noisy Channel + Bayes’ Rule • We see an observation x of a misspelled word • Find the most likely to be correct word ŵ: Bayes 53

Non-word spelling error example acress 54

Candidate generation • Words with similar spelling – Small edit distance to error – In this part, we will consider words with low Damerau-Levenshtein edit distance (insert, delete, replace and transposition) – We (almost) know how to find these! • Words with similar pronunciation – Small distance of pronunciation to error – We don’t consider how to find these! 55
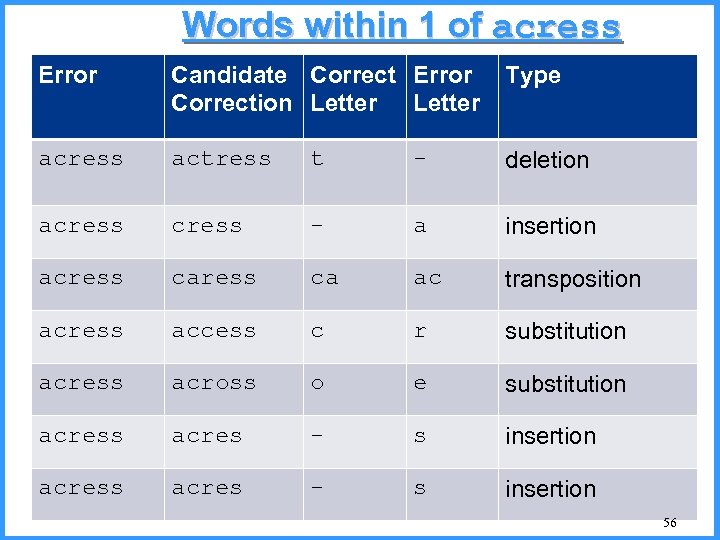
Words within 1 of acress Error Candidate Correct Error Correction Letter Type acress actress t - deletion acress - a insertion acress ca ac transposition acress access c r substitution acress across o e substitution acress acres - s insertion 56

Candidate generation • Empirical findings: – 80% of errors are within edit distance 1 – Almost all errors within edit distance 2 • Also allow insertion of space or hyphen – thisidea this idea – inlaw in-law – Isreal Is real How would you find these? 57

Note that… • We want the best spell corrections • Instead of finding the very best, we – Find a subset of pretty good corrections • (say, edit distance at most 2) – Find the best amongst them • These may not be the actual best • This is a recurring paradigm in IR including finding the best docs for a query, … – Find a good candidate set – Find the top K amongst them and return them as best 58

Back to the Formula • We see an observation x of a misspelled word. • We now have the candidate set V • Find the correct word ŵ What’s P(w)? 59

Language Model • We discuss language models in more detail later (when ranking query results) • Basic idea: – A language model associates a probability with a sequence of words – P(I, am, your, friend) is the likelihood of the sequence of words “I am your friend” – Probably P(The, brevirostrate, bibbles) is less likely – Probably P(I, am, your, couch) is also less likely 60

Types of Language Models • Unigram Language Model: The likelihood of a word is independent of previous words in the sequence, i. e. , – P(tn+1 | t 1, …, tn) = P(tn+1) – P(t 1, …, tn) = P(t 1) P(t 2) … P(tn) • Bigram Language Model: The likelihood of a word depends only on the previous word in the sequence, i. e. , – P(tn+1 | t 1, …, tn) = P(tn+1 | tn) – P(t 1, …, tn) = P(t 1|#) P(t 2|t 1) … P(tn|tn-1) 61

Language Model • Simple way to define a unigram language model • Take a big supply of words (your document collection or query log collection with T tokens) – let C(w) = # occurrences of w in the collection 62
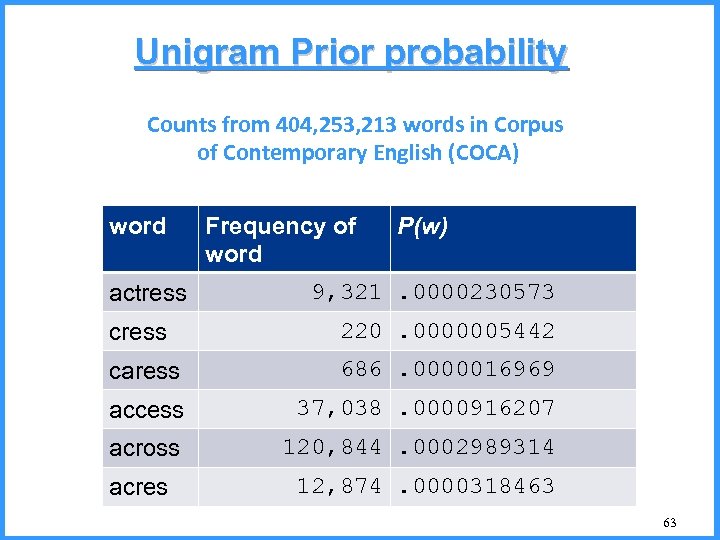
Unigram Prior probability Counts from 404, 253, 213 words in Corpus of Contemporary English (COCA) word actress Frequency of word P(w) 9, 321. 0000230573 cress 220. 0000005442 caress 686. 0000016969 access 37, 038. 0000916207 across 120, 844. 0002989314 acres 12, 874. 0000318463 63

Back to the Formula • We see an observation x of a misspelled word. • We now have the candidate set V • We have defined P(w) • Find the correct word ŵ What’s P(x|w)? 64

Edit Model Probability • Misspelled word x = x 1, x 2, x 3… xm • Correct word w = w 1, w 2, w 3, …, wn • P(x|w) = probability of the edit – (deletion/insertion/substitution/transposition) – Intuitively: How likely is it that the user typed x, when he meant to type w? • Estimate the probabilities using a large set of misspellings (e. g. , http: //norvig. com/ngrams/ ) 65
![Computing error probability: confusion “matrix” del[x, y]: count(xy typed as x) ins[x, y]: count(x Computing error probability: confusion “matrix” del[x, y]: count(xy typed as x) ins[x, y]: count(x](https://present5.com/presentation/2f884116569c6e9003cdf07d93c9dace/image-66.jpg)
Computing error probability: confusion “matrix” del[x, y]: count(xy typed as x) ins[x, y]: count(x typed as xy) sub[x, y]: count(y typed as x) trans[x, y]: count(xy typed as yx) Insertion and deletion conditioned on previous character 66

Confusion matrix for substitution 67

Channel model (Single Edit Error) Kernighan, Church, Gale 1990 68

Smoothing probabilities: Add-1 Smoothing • But if we use the confusion matrix example, unseen errors are impossible! • They’ll make the overall probability 0. That seems too harsh – e. g. , in Kernighan’s chart q a and a q are both 0, even though they’re adjacent on the keyboard! • A simple solution is to add 1 to all counts and then if there are A characters in the alphabet, to normalize appropriately: 69

Channel model for acress Candidate Correction Correct Error Letter x|w P(x|w) actress t - c|ct . 000117 cress - a a|# . 00000144 caress ca ac ac|ca . 00000164 access c r r|c . 000000209 across o e e|o . 0000093 acres - s es|e . 0000321 acres - s ss|s . 0000342 70
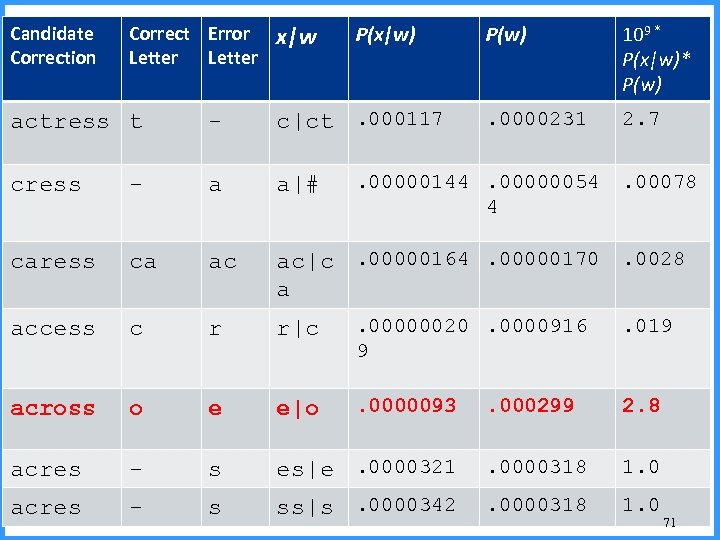
Candidate Correction Correct Error Letter x|w P(x|w) P(w) 109 * P(x|w)* P(w) . 0000231 2. 7 Noisy channel probability for acress actress t - c|ct. 000117 cress - a a|# caress ca ac ac|c. 00000164. 00000170. 0028 a access c r r|c . 00000020. 0000916 9 . 019 across o e e|o . 0000093 . 000299 2. 8 acres - s es|e. 0000321 . 0000318 1. 0 acres - s ss|s. 0000342 . 0000318 1. 0 . 00000144. 00000054 4 . 00078 71

Incorporating context words: Context-sensitive spelling correction • Determining whether actress or across is appropriate might require looking at the context of use – A unigram language model may not be appropriate! – Remember: A bigram language model conditions the probability of a word on (just) the previous word P(w 1…wn) = P(w 1)P(w 2|w 1)…P(wn|wn− 1) 72

Defining a Bigram Model • Start again with a large collection • Let w 1, w 2 be words • Let C(w 1, w 2) be the number of times that the sequence w 1, w 2 appears • Let C(w) be the number of times that w appears When will this be 0? Is that good? 73

Incorporating context words • For unigram counts, P(w) is always non-zero – if our dictionary is derived from the document collection • This won’t be true of P(wk|wk− 1). We need to smooth – We could use add-1 smoothing on this conditional distribution – But here’s a better way – interpolate a unigram and a bigram: P(wk|wk− 1) = λPuni(wk) + (1−λ)Pbi(wk|wk− 1) 74

Using a bigram language model • “a stellar and versatile acress whose combination of sass and glamour…” • Counts from the Corpus of Contemporary American English with add-1 smoothing • P(actress|versatile)=. 000021 P(whose|actress) =. 0010 • P(across|versatile) =. 000021 P(whose|across) =. 000006 • P(“versatile actress whose”) =. 000021*. 0010 = 210 x 10 -10 • P(“versatile across whose”) =. 000021*. 000006 = 1 x 10 -10 75

Putting it together using Bigram Model • To determine if the author meant to write “versatile actress whose” compute: P(versatile acress whose| versatile actress whose) P(versatile actress whose) = P(acress | actress) P(versatile actress whose) = –. 000117 x 210 x 10 -10 • To determine if the author meant to write “versatile across whose” compute similarly and get: –. 0000093 x 10 -10 76

Real Word Spelling Errors • …leaving in about fifteen minuets to go to her house. • The design an construction of the system… • Can they lave him my messages? • The study was conducted mainly be John Black. • 25 -40% of spelling errors are real words (Kukich 1992) 77

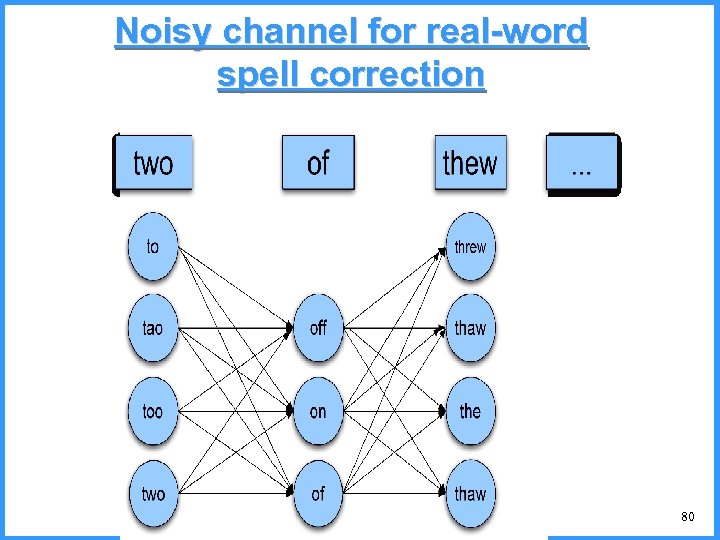
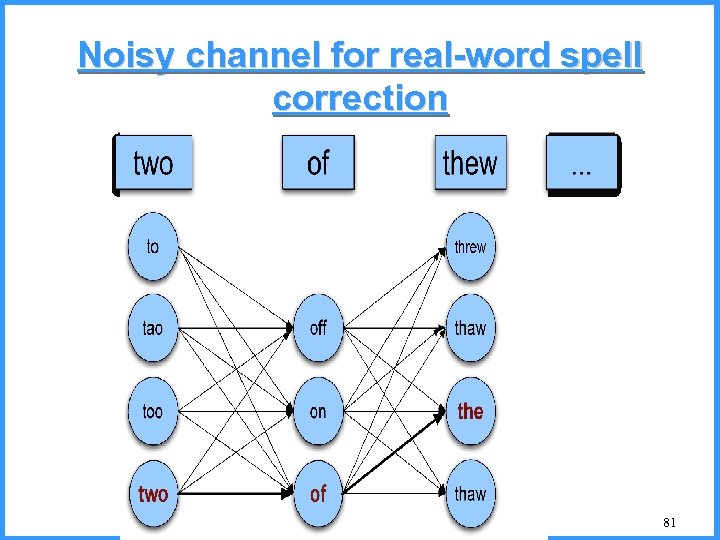
Solving real-word spelling errors • For each word in sentence (phrase, query …) – Generate candidate set • the word itself • all single-letter edits that are English words • words that are homophones • (all of this can be pre-computed!) • Choose best candidates • Noisy channel model 78

Noisy channel for real-word spell correction • Given a sentence w 1, w 2, w 3, …, wn • Generate a set of candidates for each word wi – Candidate(w 1) = {w 1, w’ 1 , w’’’ 1 , …} – Candidate(w 2) = {w 2, w’ 2 , w’’’ 2 , …} – Candidate(wn) = {wn, w’n , w’’’n , …} • Choose the sequence W that maximizes P(W | w 1, …, wn) 79
Noisy channel for real-word spell correction 80
Noisy channel for real-word spell correction 81

Simplification: One error per sentence • Out of all possible sentences with one word replaced – w 1, w’’ 2, w 3 two off thew – w 1, w 2, w’ 3 two of the – w’’’ 1, w 2, w 3 too of thew –… • Choose the sequence W that maximizes P(W | w 1, …, wn) 82

Where to get the probabilities • Language model – Unigram – Bigram – etc. • Channel model – Same as for non-word spelling correction – Plus need probability for no error, P(w|w) 83

Probability of no error • What is the channel probability for a correctly typed word? • P(“the”|“the”) – If you have a big corpus, you can estimate this percent correct • But this value depends strongly on the application –. 90 (1 error in 10 words) –. 95 (1 error in 20 words) –. 99 (1 error in 100 words) 84
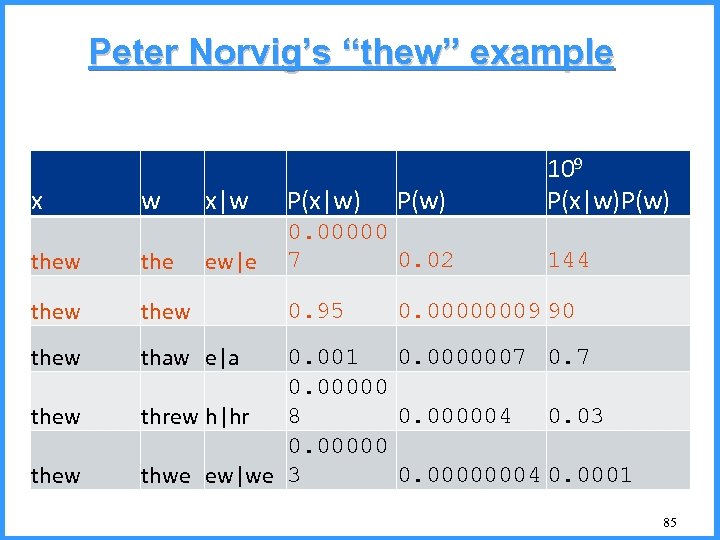
Peter Norvig’s “thew” example x w x|w P(x|w) ew|e 0. 00000 7 0. 02 thew thew P(w) 109 P(x|w)P(w) thaw e|a thew 0. 95 144 0. 00000009 90 0. 001 0. 0000007 0. 00000 8 0. 000004 0. 03 threw h|hr 0. 00000004 0. 0001 thwe ew|we 3 85
2f884116569c6e9003cdf07d93c9dace.ppt