Today s Topics Read Chapters 26 and 27

Today’s Topics • Read Chapters 26 and 27 of Textbook • 90 -min Final, Start at 8: 15 am? • I’ll Have Office Hours Next Tuesday 2 -4 pm • Do you see HW averages in Moodle? • A Short Introduction to Inductive Logic Programming (ILP) • A Short Introduction to Probabilistic Logic Learning (aka, Statistical-Relational Learning, SRL) • Knowledge-Based ANNs and Knowledge-Based SVMs 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 1

From CS 540 Fall 2015 Final There is this one history student who has read every history book in the library. x [ human(x) major. Of(x, History) { y book(y) topic. Of(y, History) location(y, Library 101) read(x, y) } ] 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 2

From CS 540 Fall 2015 Final Washing a car does not change who owns it. [You must use situation calculus here. ] x, y, s car(x) human(y) state(s) owns(y, x, s) state( result(wash(y, x), s)) owns(y, x, result(wash(y, x, s))) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 3

From CS 540 Fall 2015 Final Most students who get an A in cs 302 also get an A in cs 367. wgt = 2 x student(x) grade(x, cs 302, A) grade(x, cs 367, A) Triangles have three sides. wgt = 100 x triangle(x) number. Sides(x, 3) [You must use the notation of Markov Logic Networks here and write one wff for each of these two sentences. ] 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 4

Unification R(? x, ? y, ? x, f(? y)) R(f(? z), ? z, f(g(2)), ? w) R(f(? z), ? y, f(? z), f(? y)) R(f(? z), ? z, f(g(2)), ? w) R(f(? z), ? z, f(? z)) R(f(? z), ? z, f(g(2)), ? w) R(f(g(2)), g(2), f(g(2)), f(g(2))) R(f(g(2)), g(2), f(g(2))) { ? x/f(? z), ? y/? z, ? z/(g(2), ? w/f(g(2)) } 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 5

Natural Deduction 1) 2) 3) 4) 5) 6) P(1) Q(2) c P(c) Q(c) d, e P(d) Q(e) A(d) f, g P(f) Q(g) R(g, f) h, i R(h, i) A(h) Show a A(a) Number WFF Justification 7 Q(1) MP on 1+3, = {c/1} 8 Q(2) UR on 2+7 9 P(1) Q(2) AI on 1+8 10 R(2, 1) MP on 5+9, = {f/1, g/2} 11 A(2) MP on 6+10, = {h/2, i/1} 12 a A(a) EI on 11 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 6

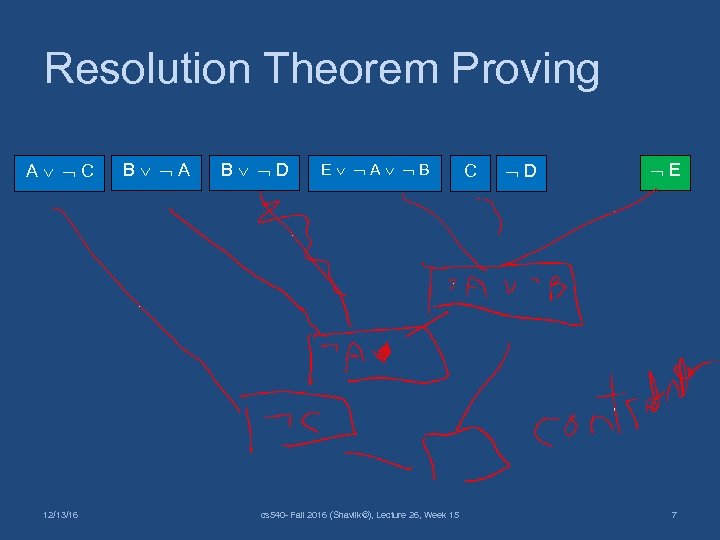Resolution Theorem Proving A C 12/13/16 B A B D E A B cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 C D E 7

Markov Logic Networks You have two Markov Logic Network rules: wgt = 2 true P wgt=3 true P (Not surprisingly, the propositional ‘true’ is true in all world states. ) What is the probability P is true? Complete World States Probability P (1/z) e 2 P (1/z) e 3 (z = e 2 + e 3) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 8

Searching for FOPC Rules What are some expansions of x, y P(x) Q(y) POS(x, y) Using R/2 x, y P(x) Q(y) R(x, x) POS(x, y) x, y P(x) Q(y) R(y, y) POS(x, y) x, y P(x) Q(y) R(x, y) POS(x, y) x, y P(x) Q(y) R(y, x) POS(x, y) x, y, z P(x) Q(y) R(x, z) POS(x, y) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 9

Inductive Logic Programming (ILP) • Use mathematical logic to – Represent training examples (goes beyond fixed-length feature vectors) – Represent learned models (FOPC rule sets) • ML work in the late ’ 70 s through early ’ 90 s was logic-based, then statistical ML ‘took over’ 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 10

Examples in FOPC Learned Concept tower(? E) if on(? E, ? A, table), on(? E, ? B, ? A). (not all have same # of ‘features’) on(ex 1, block 1, table) on(ex 1, block 2, block 1) color(ex 1, block 1, blue) color(ex 1, block 2, blue) size(ex 1, block 1, large) size(ex 1, block 2, small) Pos. Ex 1 Pos. Ex 2 < a much larger number of facts are needed to describe example 2 > 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 11

Searching for a Good Rule (propositional-logic version) P is always true P if A P if B and C 12/13/16 P if C P if B and D cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 12

All Possible Extensions of a Clause (capital letters are variables) Assume we are expanding this node q(X, Z) p(X, Y) What are the possible extensions using r/3 ? r(X, X, X) r(Y, Y, Y) r(Z, Z, Z) r(1, 1, 1) r(X, Y, Z) r(Z, Y, X) r(X, X, Y) r(X, X, 1) r(X, Y, A) r(X, A, B) r(A, A, A) r(A, B, 1) and many more … Choose from: old variables, constants, new vars Huge branching factor in our search! 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 13

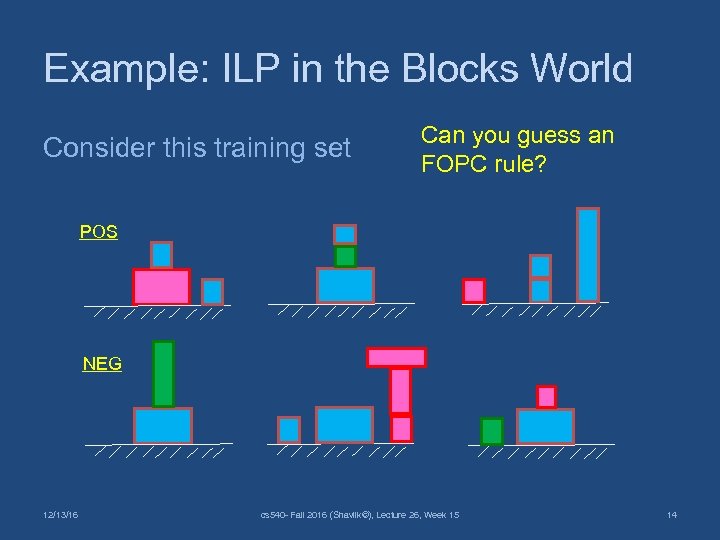Example: ILP in the Blocks World Consider this training set Can you guess an FOPC rule? POS NEG 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 14

Searching for a Good Rule (FOPC version; cap letters are vars) + true POS - … on(X, Y) POS blue(X) POS tall(X) POS Assume we have: tall(X), wide(Y), square(X), on(X, Y), red(X), green(X), blue(X), block(X) POSSIBLE RULE LEARNED: If on(X, Y) block(Y) blue(X) POS - hard to learn with fixed-length feature vectors! 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 15

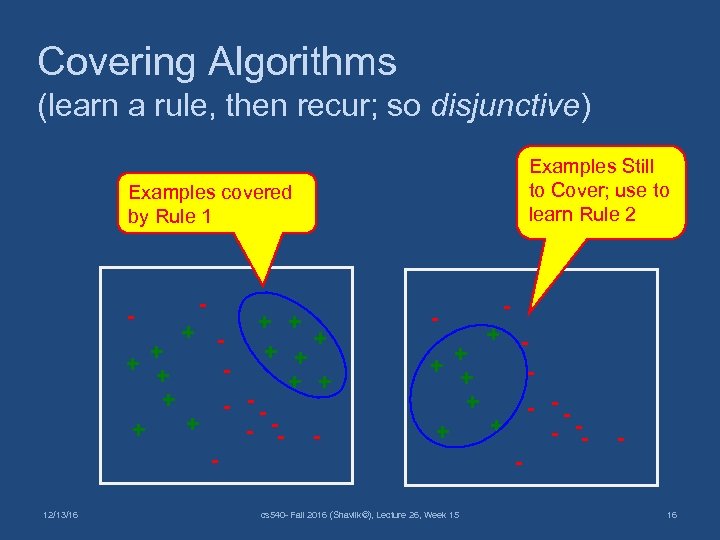Covering Algorithms (learn a rule, then recur; so disjunctive) Examples Still to Cover; use to learn Rule 2 Examples covered by Rule 1 + + + + + - -+ -- + + + - 12/13/16 - - + + - -+ -+ - cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 - - + - 16

Using Background Knowledge (BK) in ILP • Now consider adding some domain knowledge about the task being learned • For example If Q, R, and W are all true Then you can infer Z is true • Can also do arithmetic, etc in BK rule bodies If SOME_TRIG_CALCS_OUTSIDE_OF_LOGIC Then open. Passing. Lane(P 1, P 2, Radius, Angle) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 17

Searching for a Good Rule using Deduced Features (eg, Z) P is always true P if Z P if A P if B P if C Note that more BK can lead to slower learning! But hopefully less search depth needed 12/13/16 P if B & Z P if B and C P if B and D cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 18

ILP Wrapup • Use best-first search with a large beam • Commonly used scoring function #pos. Ex. Covered - #neg. Ex. Coved – rule. Length • Performs ML without requiring fixed-length-feature-vectors • Produces human-readable rules (straightforward to convert FOPC to English) • Can be slow due to large search space • Appealing ‘inner loop’ for prob logic learning 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 19

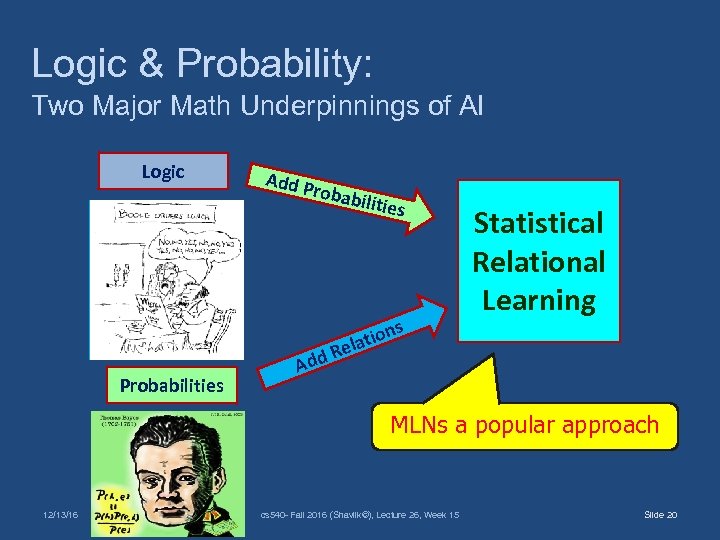Logic & Probability: Two Major Math Underpinnings of AI Logic Add P robab ilities s Probabilities Add Statistical Relational Learning n latio Re MLNs a popular approach 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 Slide 20

Statistical Relational Learning (Intro to SRL, Getoor & Tasker (eds), MIT Press, 2007) • Pure Logic Too ‘Fragile’ everything must be either true or false • Pure Statistics Doesn’t Capture/Accept General Knowledge Well (tell it once rather than label N ex’s) x human(x) y mother. Of(x, y) • Many Approaches Created Over the Years, Especially Last Few including some at UWisc 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 21

Pedro Domingos Markov Logic Networks (Richards and Domingos, MLj, 2006) • Use FOPC, but add weights to formulae (‘syntax’) wgt=10 x, y, z mother. Of(x, z) father. Of(y, z) married(x, y) - weights represent ‘penalty’ if a candidate world state violates the rule - for ‘pure’ logic, wgt = ∞ • Formulae interpreted (‘semantics’) as compact way to specify a type of graphical model called a Markov Net – like a Bayes net, but undirected arcs – probabilities in Markov nets specified by clique potentials, but we won’t cover them in cs 540 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 22

Using an MLN (‘Inference’) • Assume we have a large knowledge base of probabilistic logic rules • Assume we are given the truth values of N predicates (the ‘evidence’) • We may be asked to estimate the most probable joint setting for M ‘query’ predicates • Brute-force solution – Consider 2 M possible ‘complete world states’ – Calculate truth value of all grounded formula in each state – Return one with smallest total penalty for violated MLN rules (or, equivalently, the one with largest sum of satisfied rules) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 Slide 23

Probability of Candidate World States Prob(specific world state) (1/Z) exp( weights of grounded formulae that are true in this world state) Z is a normalizing term; we need to sum over all possible world states (challenging to estimate) - A world state is a conjunction of predicates (eg, married(John, Sue), …, friends(Bill, Ann) ) - if we only want the most probable world state, we don’t need to compute Z If a world state violates a rule with infinite weight, probability of that world state is zero (why? ) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 24

Grounding the MLN Formulae (replacing variables with constants) • Assume we have this domain knowledge wgt = 2 x, y P(x, y) Q(x) wgt = 3 x P(x, 1) (R(1) R(x)) • And these constants: 1 and 2 • So we have these ‘grounded’ rules (wgts not shown): P(1, 1) Q(1) P(1, 2) Q(1) P(2, 1) Q(2) P(1, 1) R(1) P(2, 2) Q(2) P(2, 1) (R(1) R(2)) • Aside: Each grounded rule becomes a clique in Markov network (like a CPT in a Bayes Net) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 25

Simple MLN Example Have: wgt=2 P Q wgt=7 P Q Four possible world states P Q Probability False (1/Z) e 2+0 1 / e 8 False True (1/Z) e 2+7 1 / e True False (1/Z) e 0+7 1 / e 3 True (1/Z) e 2+7 1 / e What is prob(P=true & Q=false) in ‘std’ logic? The normalizing term: Z = e 2 + e 9 + e 7 + e 9 e 10 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 26

Collective Classification • Assume we need to predict the outputs for N examples • Could knowing (probability) example i is true impact (probability) example j is true? Ie, relaxing the iid assumption about examples • For instance “If Alice and Bob are friends, then if Alice likes a movie, Bob (probably) does as well. ” 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 27

Collective Classification in MLNs • Imagine we have a bunch of inference rules for predicting likes(Person, Food) • We could add this to our MLN If lives. In(? Person 1, ? City) lives. In(? Person 2, ? City) isa. Food(? Food) Then [ likes(? Person 1, ? Food) likes(? Person 2, ? Food) ] with wgt = 3 So if we predicted likes of N people, the MLN would be encouraged to give consistent 12/13/16 answers “People in the same city generally like the same sorts of food” cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 28

Don’t buy these → A Famous MLN Example (first rule modified to use ↔) “Smoking frequently causes cancer. ” wgt = 3 x smokes(x) ↔ cancer(x) // Assume it’s the ONLY cause “Friends of smokers are likely to smoke. ” wgt = 2 x, y friends(x, y) ˄ smokes(x) smokes(y) Assume below are our facts and we want to know the probs of the four world states involving smoking or not of John and Mary A simple collective classification example (try yourself with THREE people!) friends(Mary, Mary), friends(Mary, John), ¬ cancer(Mary) friends(John, Mary), friends(John, John), cancer(John) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 29

A Famous MLN Example (2) “Smoking frequently causes cancer. ” GROUNDED wgt = 3 smokes(J) ↔ cancer(J) wgt = 3 smokes(M) ↔ cancer(M) “Friends of smokers are likely to smoke. ” GROUNDED wgt = 2 friends(M, M) ˄ smokes(M) wgt = 2 friends(M, J) ˄ smokes(M) smokes(J) wgt = 2 friends(J, M) ˄ smokes(J) smokes(M) wgt = 2 friends(J, J ) ˄ smokes(J) FACTS friends(M, M), friends(M, J) , ¬ cancer(M) friends(J, M), friends(J, J), cancer(J) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 30

A Famous MLN Example (3) Possible Complete Word States (1) friends(M, M), friends(M, J) , friends(J, M), friends(J, J) ¬ smokes(M), ¬ smokes(J), ¬ cancer(Mary), cancer(John) (2) friends(M, M), friends(M, J), friends(J, M), friends(J, J) ¬ smokes(M), smokes(J), ¬ cancer(Mary), cancer(John) (3) friends(M, M), friends(M, J), friends(J, M), friends(J, J) smokes(M), ¬ smokes(J), ¬ cancer(Mary), cancer(John) (4) friends(M, M), friends(M, J), friends(J, M), friends(J, J) smokes(M), smokes(J), ¬ cancer(Mary), cancer(John) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 31

A Famous MLN Example (4) Possible Complete Word States (1) friends(M, M), friends(M, J), friends(J, M), friends(J, J) ¬ smokes(M), ¬ smokes(J), ¬ cancer(M), cancer(J) “Smoking frequently causes cancer. ” GROUNDED wgt = 3 smokes(J) ↔ cancer(J) wgt = 3 smokes(M) ↔ cancer(M) F T Sum of Wgts = 0 + 3 + 2 + 2 = 11 “Friends of smokers are likely to smoke. ” GROUNDED wgt = 2 ¬ friends(M, M) ˅ ¬ smokes(M) ˅ smokes(M) wgt = 2 ¬ friends(M, J) ˅ ¬ smokes(M) ˅ smokes(J) wgt = 2 ¬ friends(J, M) ˅ ¬ smokes(J) ˅ smokes(M) wgt = 2 ¬ friends(J, J ) ˅ ¬ smokes(J) ˅ smokes(J) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 T T 32

A Famous MLN Example (5) Possible Complete Word States (2) friends(M, M), friends(M, J) , friends(J, M), friends(J, J) ¬ smokes(M), smokes(J), ¬ cancer(M), cancer(J) “Smoking frequently causes cancer. ” GROUNDED wgt = 3 smokes(J) ↔ cancer(J) wgt = 3 smokes(M) ↔ cancer(M) T T Sum of Wgts = 3 + 2 + 0 + 2 = 12 “Friends of smokers are likely to smoke. ” GROUNDED wgt = 2 ¬ friends(M, M) ˅ ¬ smokes(M) ˅ smokes(M) wgt = 2 ¬ friends(M, J) ˅ ¬ smokes(M) ˅ smokes(J) wgt = 2 ¬ friends(J, M) ˅ ¬ smokes(J) ˅ smokes(M) wgt = 2 ¬ friends(J, J ˅ ¬ smokes(J) ˅ smokes(J) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 T T F T 33

A Famous MLN Example (6) Possible Complete Word States (3) friends(M, M), friends(M, J), friends(J, M), friends(J, J) smokes(M), ¬ smokes(J), ¬ cancer(M), cancer(J) “Smoking frequently causes cancer. ” GROUNDED wgt = 3 smokes(J) ↔ cancer(J) wgt = 3 smokes(M) ↔ cancer(M) F F Sum of Wgts = 0 + 2 + 0 + 2 = 6 “Friends of smokers are likely to smoke. ” GROUNDED wgt = 2 ¬ friends(M, M) ˅ ¬ smokes(M) ˅ smokes(M) wgt = 2 ¬ friends(M, J) ˅ ¬ smokes(M) ˅ smokes(J) wgt = 2 ¬ friends(J, M) ˅ ¬ smokes(J) ˅ smokes(M) wgt = 2 ¬ friends(J, J) ˅ ¬ smokes(J) ˅ smokes(J) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 T F T T 34

A Famous MLN Example (7) Possible Complete Word States (4) friends(M, M), friends(M, J), friends(J, M), friends(J, J) smokes(M), smokes(J), ¬ cancer(M), cancer(J) “Smoking frequently causes cancer. ” GROUNDED wgt = 3 smokes(J) ↔ cancer(J) wgt = 3 smokes(M) ↔ cancer(M) T F Sum of Wgts = 3 + 0 + 2 + 2 = 11 “Friends of smokers are likely to smoke. ” GROUNDED wgt = 2 ¬ friends(M, M) ˅ ¬ smokes(M) ˅ smokes(M) wgt = 2 ¬ friends(M, J) ˅ ¬ smokes(M) ˅ smokes(J) wgt = 2 ¬ friends(J, M) ˅ ¬ smokes(J) ˅ smokes(M) wgt = 2 ¬ friends(J, J) ˅ ¬ smokes(J) ˅ smokes(J) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 T T 35

A Famous MLN Example (8) Possible Complete Word States Sum of Wgts of Satisfied Rules (1) friends(M, M), friends(M, J) , friends(J, M), friends(J, J) ¬ smokes(M), ¬ smokes(J), ¬ cancer(Mary), cancer(John) 11 (2) friends(M, M), friends(M, J) , friends(J, M), friends(J, J) ¬ smokes(M), smokes(J), ¬ cancer(Mary), cancer(John) 12 (3) friends(M, M), friends(M, J), friends(J, M), friends(J, J) smokes(M), ¬ smokes(J), ¬ cancer(Mary), cancer(John) 6 (4) friends(M, M), friends(M, J), friends(J, M), friends(J, J) smokes(M), smokes(J), ¬ cancer(Mary), cancer(John) 11 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 36

A Famous MLN Example (8) Possible Complete Word States (1) friends(M, M), friends(M, J) , friends(J, M), friends(J, J) Sum of Wgts of Satisfied Rules 11 Prob = e 11 / Z 1 / 4. 7 = 0. 21 12 Prob = e 12 / Z e / 4. 7 = 0. 58 ¬ smokes(M), ¬ smokes(J), ¬ cancer(Mary), cancer(John) (2) friends(M, M), friends(M, J) , friends(J, M), friends(J, J) ¬ smokes(M), smokes(J), ¬ cancer(Mary), cancer(John) (3) friends(M, M), friends(M, J), friends(J, M), friends(J, J) 6 Prob = e 6 / Z (1 / 5) e-5 0. 001 smokes(M), ¬ smokes(J), ¬ cancer(Mary), cancer(John) (4) friends(M, M), friends(M, J), friends(J, M), friends(J, J) 11 Prob = e 11 / Z 1 / 4. 7 smokes(M), smokes(J), ¬ cancer(Mary), cancer(John) = 0. 21 Z 12/13/16 = e 11 + e 12 + e 6 + e 11 = e 11 (1 + e-5 + 1) 4. 7 e 11 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 37

A Famous MLN Example (9) (1) ¬ smokes(M), ¬ smokes(J), ¬ cancer(M), cancer(J) lost 3 pts because John had cancer yet wasn’t a smoker (2) ¬ smokes(M), smokes(J), ¬ cancer(M), cancer(J) lost 2 pts because Friends J and M had diff smoking habits (3) smokes(M), ¬ smokes(J), ¬ cancer(M), cancer(J) lost 8 pts because of three reasons (4) smokes(M), smokes(J), ¬ cancer(M), cancer(J) lost 3 pts because Mary smoked but didn’t have cancer If we had wgt=3 smoking cancer and wgt=2 cancer smoking Then (1) and (4) would have scored differently (but slides already too crowded!) If we had more people, we would have more clearly seen influence of collective classification - try it yourself! 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 38

Handling Probabilistic Evidence - What if the Given’s are Uncertain? • Assume we know Prob( q(1, 2) ) = 0. 85 • We can represent this as Prob( observed. Q(1, 2) ) = 1. 0 // ie, absolute evidence wgt = 2 observed. Q(1, 2) q(1, 2) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 39

Grounded Networks can be Very LARGE! Given wgt=2 x, y, z Friends(x, y) Friends(y, z) Friends(x, z) and a world with 109 people How big is the grounded network? 1018 nodes since we need all groundings of Friends(? X, ? Y) (and the number of world states is 21018) So SAMPLING methods needed (and have been published) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 40

Knowledge-Base Population (http: //www. nist. gov/tac/2015/KBP/) Given: Text Corpus (ie, ordinary English) Do: Extract Facts about People Born(Person, Date) Attended. College(Person, College, Date. Range) Employed. By(Person, Company, Date. Range) Spouse. Of(Person. A, Person. B, Date. Range) Parent. Of(Person. A, Person. B, Date. Range) Died(Person, Date) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 41

Sample Advice for Collective Classification? What might we say to an ML working on KBP? Think about constraints across the relations People are only married to one person at a time. People usually have fewer than five children and rarely more than ten. Typically one graduates from college in their 20’s. Most people only have one job at a time. One cannot go to college before they were born or after they died. Almost always your children are born after you were. People tend to marry people of about the same age. People rarely live to be over 100 years & never over 125. People don’t marry their children. … 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 42

Sample Advice for Collective Classification? What might we say to an ML working on KBP? When converted to MLN notation, Think about constraints across the relations these sentences of common-sense knowledge improve the results of People are only married to one person at a time. information-extraction algorithms People usually have fewer than five children and rarely more than ten. that simply extract each relation Typically one graduates from college in their 20’s. independently (and noisily) Most people only have one job at a time. One cannot go to college before they were born or after they died. Almost always your children are born after you were. People tend to marry people of about the same age. People rarely live to be over 100 years & never over 125. People don’t marry their children. … 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 43

Scaling Up MLN Inference (see ICDM ‘ 12 paper by Niu et al. titled “Scaling Inference for Markov Logic via Dual Decomposition”) We successfully ran in 1 day on the Knowledge Base Population task with – 240 million facts (from 500 million web articles) – 64 billion logic sentences in the ground MLN – 5 terrabyte database (from Green. Plum, Inc) – 256 GB RAM, 40 cores on 4 machines – See `Deep. Dive/Wisci’ at www. youtube. com/user/Hazy. Research/videos 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 Slide 44

Learning MLNs Like with Bayes Nets, need to learn – Structure (ie, a rule set; could be given by user) – Weights (can use gradient descent) – There is a small literature on these tasks (some by my group) 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 45

MLN Challenges • Estimating probabilities (‘inference’) can be cpu-intensive usually need to use clever sampling methods since # of world states is 0(2 N) • Interesting direction: lifted inference (reason at first-order level, rather than on grounded network) • Structure learning and refinement are major challenges 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 46

MLN Wrapup • Appealing combo of first-order logic and prob/stats (the two primary math underpinnings of AI) • Impressive results on real-world tasks • Appealing approach to ‘knowledge refinement’ 1. Humans write (buggy) common-sense rules 2. MLN algo learns weights (and maybe ‘edits’ rules) • Computationally demanding (both learning MLNs and using them to answer queries) • Other approaches to probabilistic logic exist; vibrant/exciting research area 12/13/16 cs 540 - Fall 2016 (Shavlik©), Lecture 26, Week 15 47

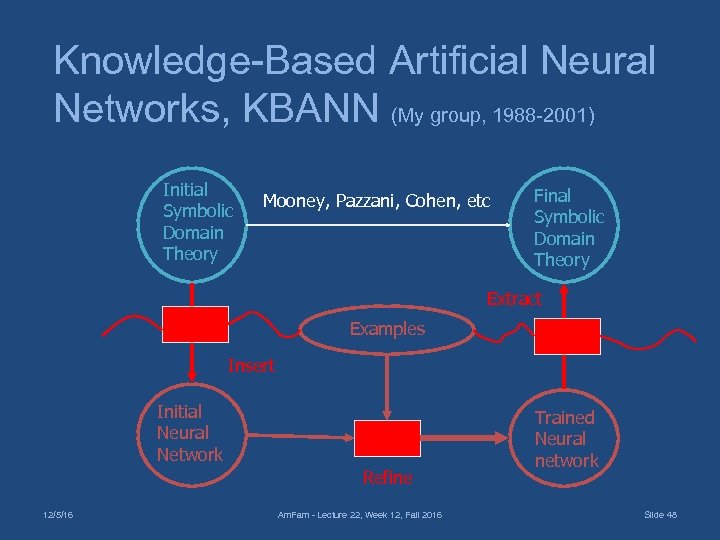Knowledge-Based Artificial Neural Networks, KBANN (My group, 1988 -2001) Initial Symbolic Domain Theory Mooney, Pazzani, Cohen, etc Final Symbolic Domain Theory Extract Examples Insert Initial Neural Network Refine 12/5/16 Am. Fam - Lecture 22, Week 12, Fall 2016 Trained Neural network Slide 48

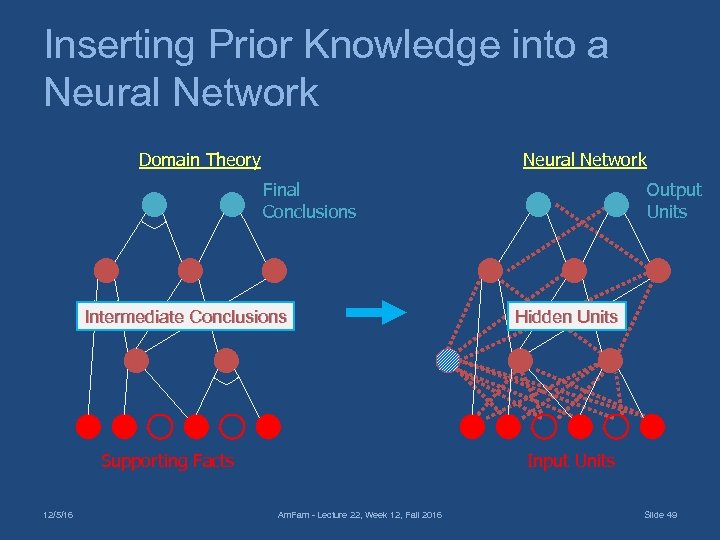Inserting Prior Knowledge into a Neural Network Domain Theory Output Units Final Conclusions Intermediate Conclusions Supporting Facts 12/5/16 Hidden Units Input Units Am. Fam - Lecture 22, Week 12, Fall 2016 Slide 49

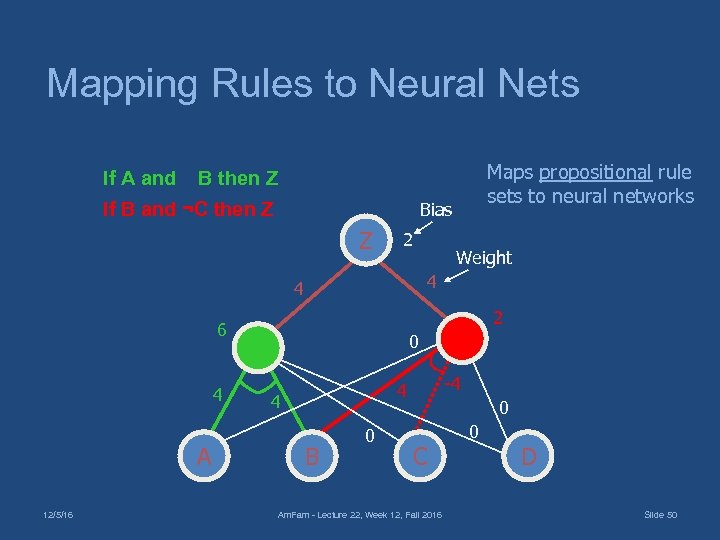Mapping Rules to Neural Nets If A and Bias If B and ¬C then Z Z 2 2 6 4 A Weight 4 4 12/5/16 Maps propositional rule sets to neural networks B then Z 0 -4 4 4 B 0 0 C Am. Fam - Lecture 22, Week 12, Fall 2016 0 D Slide 50

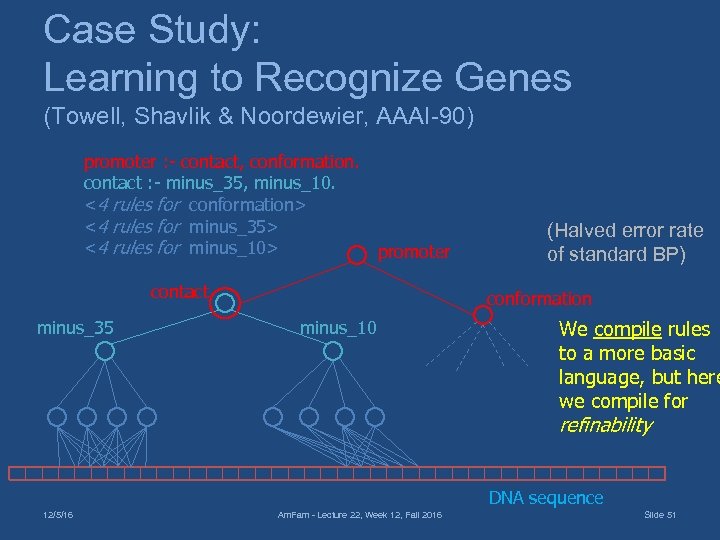Case Study: Learning to Recognize Genes (Towell, Shavlik & Noordewier, AAAI-90) promoter : - contact, conformation. contact : - minus_35, minus_10. <4 rules for conformation> <4 rules for minus_35> <4 rules for minus_10> promoter contact minus_35 (Halved error rate of standard BP) conformation minus_10 We compile rules to a more basic language, but here we compile for refinability DNA sequence 12/5/16 Am. Fam - Lecture 22, Week 12, Fall 2016 Slide 51

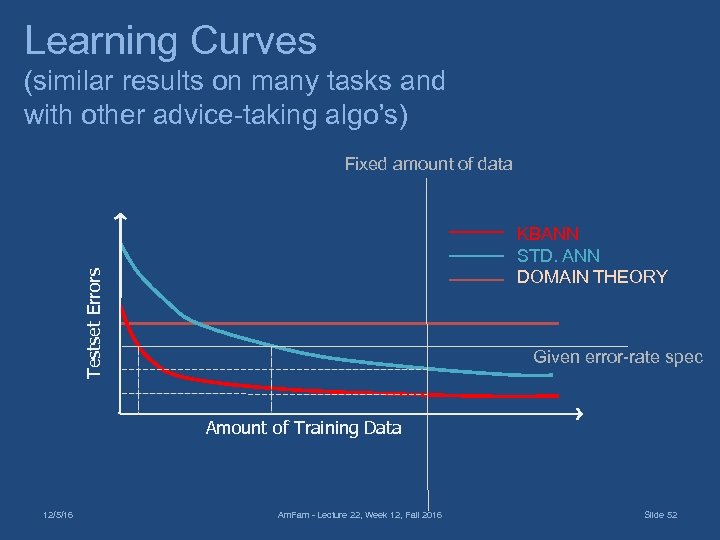Learning Curves (similar results on many tasks and with other advice-taking algo’s) Fixed amount of data Testset Errors KBANN STD. ANN DOMAIN THEORY Given error-rate spec Amount of Training Data 12/5/16 Am. Fam - Lecture 22, Week 12, Fall 2016 Slide 52

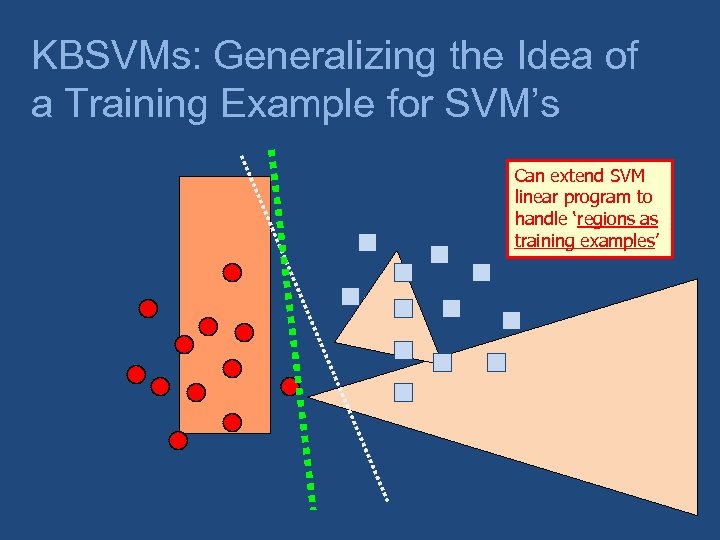KBSVMs: Generalizing the Idea of a Training Example for SVM’s Can extend SVM linear program to handle ‘regions as training examples’

KBANN Recap • Use symbolic knowledge to make an initial guess at the concept description Standard neural-net approaches make a random guess • Use training examples to refine the initial guess (‘early stopping’ reduces overfitting) • Nicely maps to incremental (aka online) machine learning • Valuable to show user the learned model expressed in symbols rather than numbers 12/5/16 Am. Fam - Lecture 22, Week 12, Fall 2016 Slide 54