Today s agendum Induced emf You must understand how

Today’s agendum: Induced emf. You must understand how changing magnetic flux can induce an emf, and be able to determine the direction of the induced emf. Faraday’s “Law. ” You must be able to use Faraday’s “Law” to calculate the emf induced in a circuit. Lenz’s “Law. ” You must be able to use Lenz’s “Law” to determine the direction induced current, and therefore induced emf. Generators (part 1). You must understand how generators work, and use Faraday’s “Law” to calculate numerical values of parameters associated with generators. 2

Induced emf and Faraday’s “Law” Magnetic Induction We have found that an electric current can give rise to a magnetic field… I wonder if a magnetic field can somehow give rise to an electric current… 3

It is observed experimentally that changes in magnetic flux induce an emf in a conductor. B An electric current is induced if there is a closed circuit (e. g. , loop of wire) in the changing magnetic flux. I B A constant magnetic flux does not induce an emf—it takes a changing magnetic flux. 4

Passing the coil through the magnet would induce an emf in the coil. They need to calibrate their meter! 5

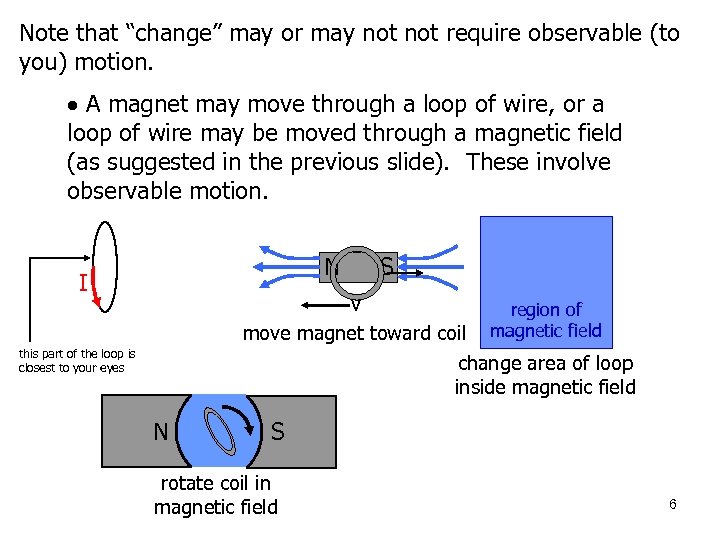Note that “change” may or may not require observable (to you) motion. wire, A magnet may move through a loop of wire or a loop of wire may be moved through a magnetic field (as suggested in the previous slide). These involve observable motion. N I S v region of move magnet toward coil magnetic field change area of loop inside magnetic field this part of the loop is closest to your eyes N S rotate coil in magnetic field 6

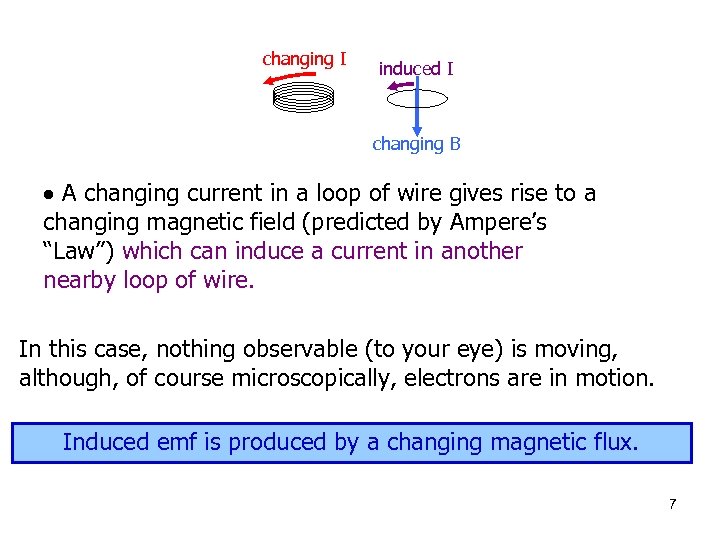changing I induced I changing B A changing current in a loop of wire gives rise to a changing magnetic field (predicted by Ampere’s “Law”) which can induce a current in another nearby loop of wire. In this case, nothing observable (to your eye) is moving, although, of course microscopically, electrons are in motion. Induced emf is produced by a changing magnetic flux. 7

Today’s agendum: Induced emf. You must understand how changing magnetic flux can induce an emf, and be able to determine the direction of the induced emf. Faraday’s “Law. ” You must be able to use Faraday’s “Law” to calculate the emf induced in a circuit. Lenz’s “Law. ” You must be able to use Lenz’s “Law” to determine the direction induced current, and therefore induced emf. Generators (part 1). You must understand how generators work, and use Faraday’s “Law” to calculate numerical values of parameters associated with generators. 8

We can quantify the induced emf described qualitatively in the last few slides by using magnetic flux. Experimentally, if the flux through N loops of wire changes by d B in a time dt, the induced emf is Faraday’s “Law” of Magnetic Induction Faraday’s “Law” of Induction is one of the fundamental laws of electricity and magnetism. I wonder why the – sign… Your text, pages 997 -998, shows how to determine the direction of the induced emf. Argh! Lenz’s Law, coming soon, is much easier. 9

Faraday’s “Law” of Magnetic Induction where the magnetic flux is This is another version of Faraday’s “Law”: We’ll use this version in a later lecture. In a future lecture, we’ll work with Web page with pictures of a whole bunch of applications: http: //sol. sci. uop. edu/~jfalward/electromagneticinduction. html 10

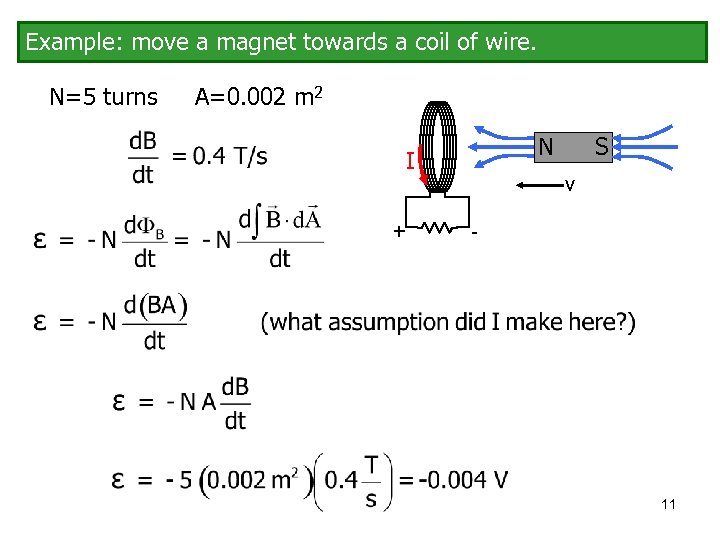Example: move a magnet towards a coil of wire. N=5 turns A=0. 002 m 2 N I + S v - 11

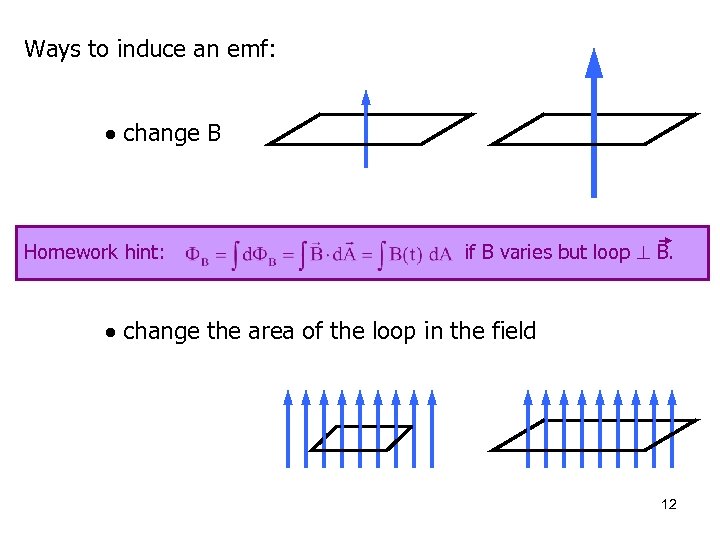Ways to induce an emf: change B Homework hint: if B varies but loop B. change the area of the loop in the field 12

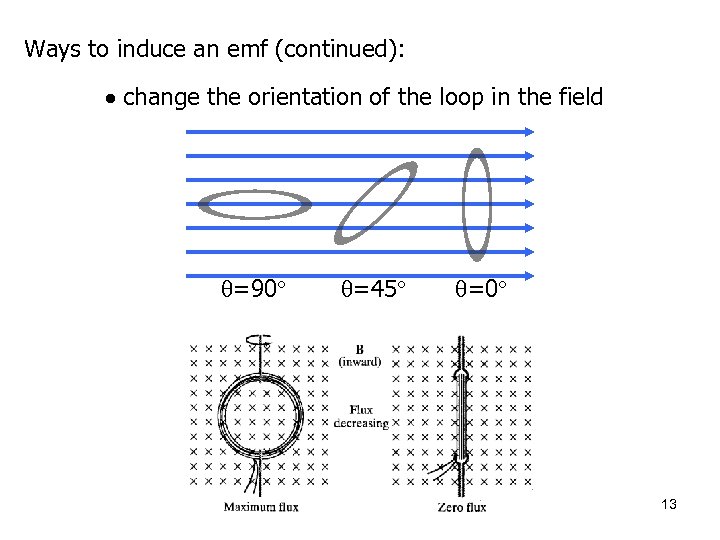Ways to induce an emf (continued): change the orientation of the loop in the field =90 =45 =0 13

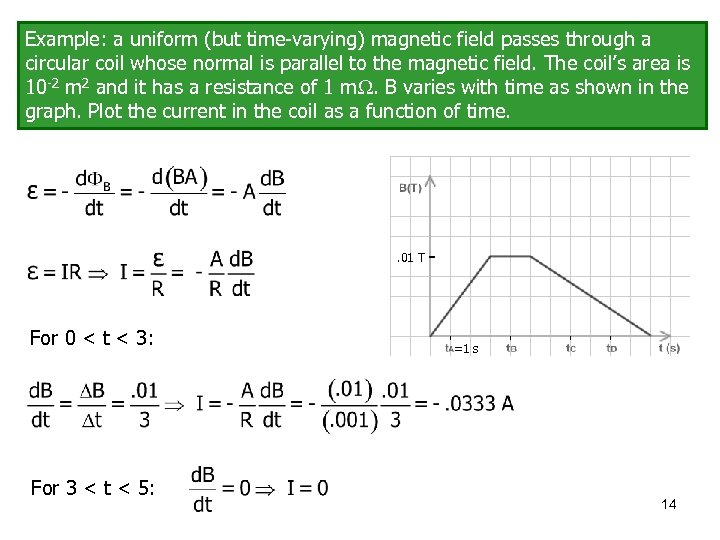Example: a uniform (but time-varying) magnetic field passes through a circular coil whose normal is parallel to the magnetic field. The coil’s area is 10 -2 m 2 and it has a resistance of 1 m. B varies with time as shown in the graph. Plot the current in the coil as a function of time. . 01 T For 0 < t < 3: For 3 < t < 5: =1 s 14

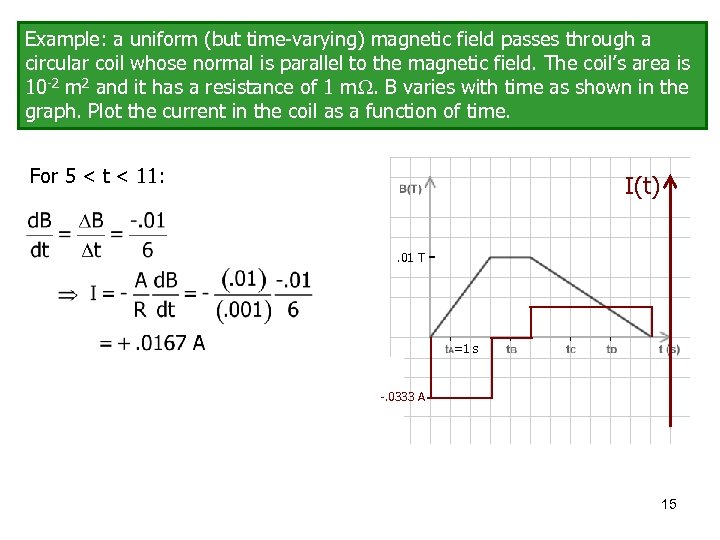Example: a uniform (but time-varying) magnetic field passes through a circular coil whose normal is parallel to the magnetic field. The coil’s area is 10 -2 m 2 and it has a resistance of 1 m. B varies with time as shown in the graph. Plot the current in the coil as a function of time. For 5 < t < 11: I(t). 01 T =1 s -. 0333 A 15

Today’s agendum: Induced emf. You must understand how changing magnetic flux can induce an emf, and be able to determine the direction of the induced emf. Faraday’s “Law. ” You must be able to use Faraday’s “Law” to calculate the emf induced in a circuit. Lenz’s “Law. ” You must be able to use Lenz’s “Law” to determine the direction induced current, and therefore induced emf. Generators (part 1). You must understand how generators work, and use Faraday’s “Law” to calculate numerical values of parameters associated with generators. 16

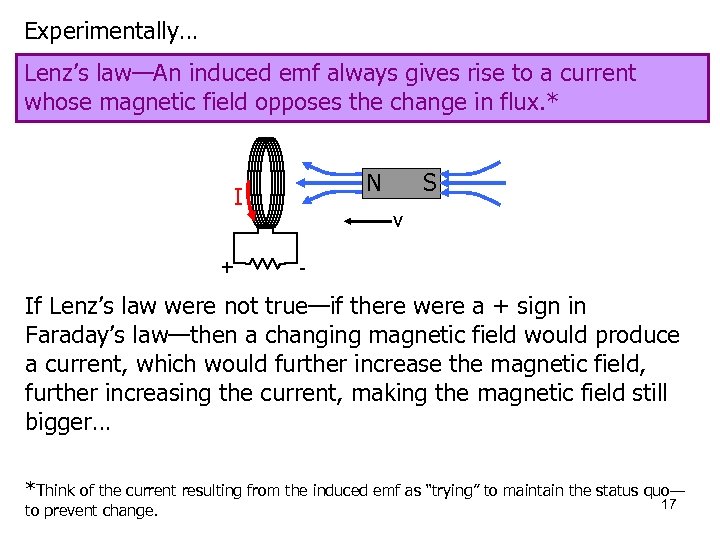Experimentally… Lenz’s law—An induced emf always gives rise to a current whose magnetic field opposes the change in flux. * N I + S v - If Lenz’s law were not true—if there were a + sign in Faraday’s law—then a changing magnetic field would produce a current, which would further increase the magnetic field, further increasing the current, making the magnetic field still bigger… *Think of the current resulting from the induced emf as “trying” to maintain the status quo— to prevent change. 17

…violating conservation of energy and ripping apart the very fabric of the universe… 18

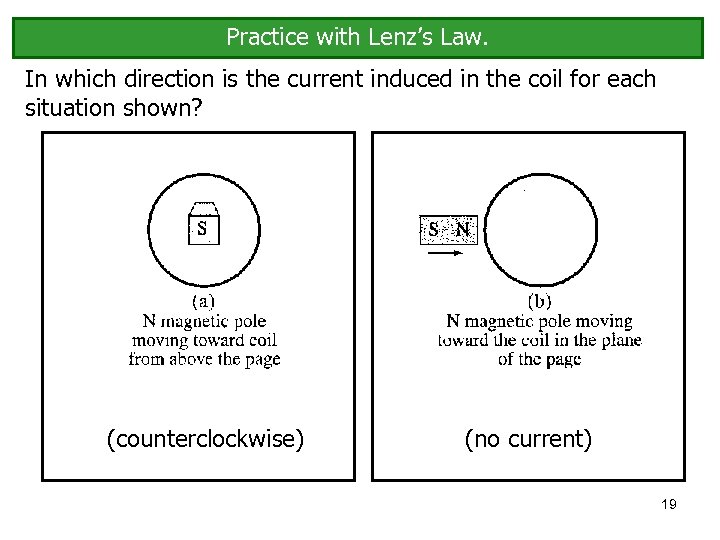Practice with Lenz’s Law. In which direction is the current induced in the coil for each situation shown? (counterclockwise) (no current) 19

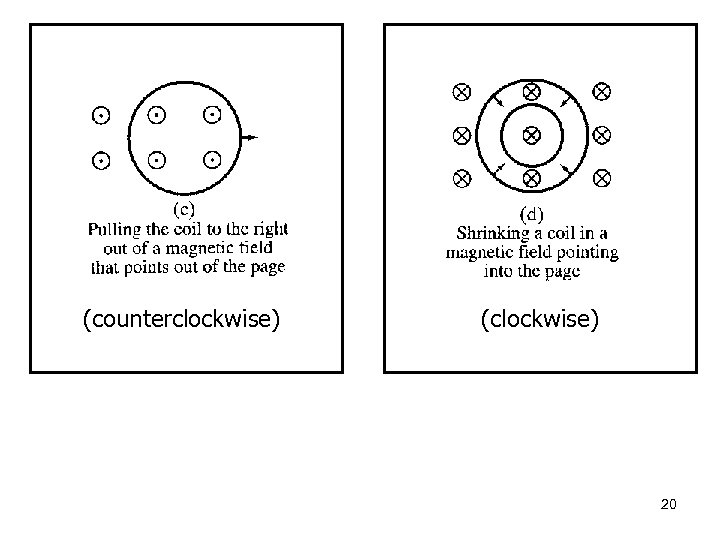(counterclockwise) (clockwise) 20

Rotating the coil about the vertical diameter by pulling the left side toward the reader and pushing the right side away from the reader in a magnetic field that points from right to left in the plane of the page. (counterclockwise) Remember Now that you are experts on the application of Lenz’s “Law”, remember this: You can use Faraday’s “Law” to calculate the magnitude of the emf (or whatever the problem wants. Then use Lenz’s “Law” to figure out the direction of the induced current (or the direction of whatever the problem 21 wants).

Today’s agendum: Induced emf. You must understand how changing magnetic flux can induce an emf, and be able to determine the direction of the induced emf. Faraday’s “Law. ” You must be able to use Faraday’s “Law” to calculate the emf induced in a circuit. Lenz’s “Law. ” You must be able to use Lenz’s “Law” to determine the direction induced current, and therefore induced emf. Generators. You must understand how generators work, and use Faraday’s “Law” to calculate numerical values of parameters associated with generators. 22

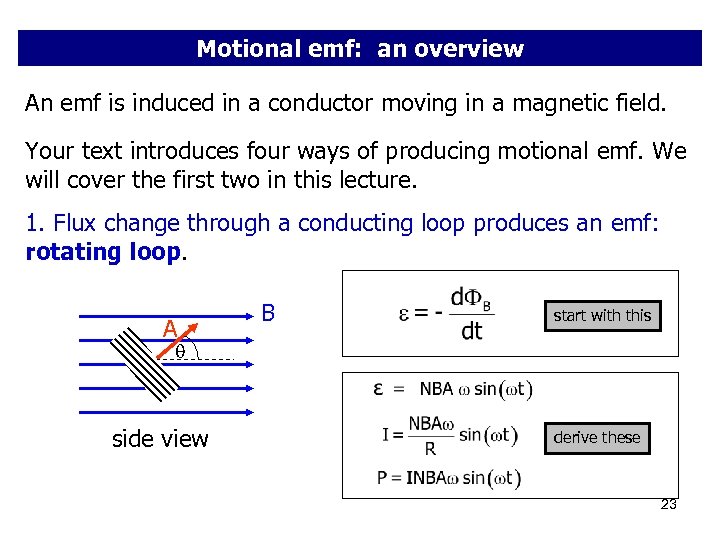Motional emf: an overview An emf is induced in a conductor moving in a magnetic field. Your text introduces four ways of producing motional emf. We will cover the first two in this lecture. 1. Flux change through a conducting loop produces an emf: rotating loop. A B start with this side view derive these 23

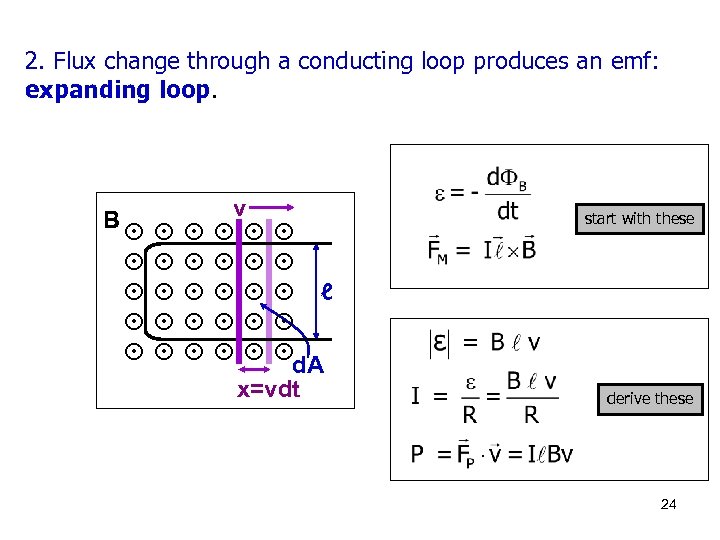2. Flux change through a conducting loop produces an emf: expanding loop. B v ℓ d. A x=vdt start with these derive these 24

Next time we will look at two more examples of motional emf… 3. Conductor moving in a magnetic field experiences an emf: magnetic force on charged particles. B v – + start with these ℓ derive this You could also solve this using Faraday’s” Law” by constructing a “virtual” circuit using “virtual” conductors. 25

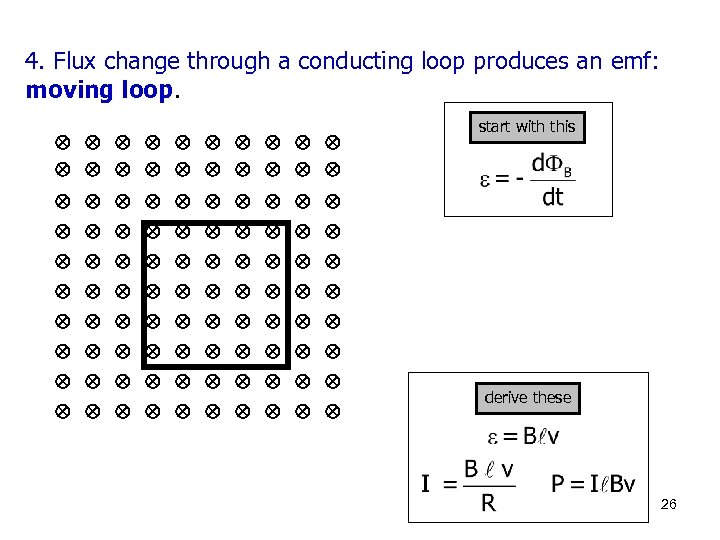4. Flux change through a conducting loop produces an emf: moving loop. start with this derive these 26

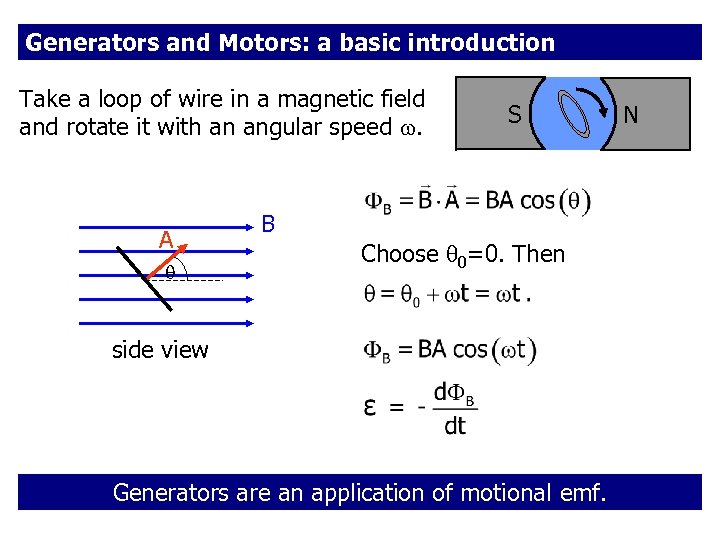Generators and Motors: a basic introduction Take a loop of wire in a magnetic field and rotate it with an angular speed . A S N B Choose 0=0. Then side view Generators are an application of motional emf. 27

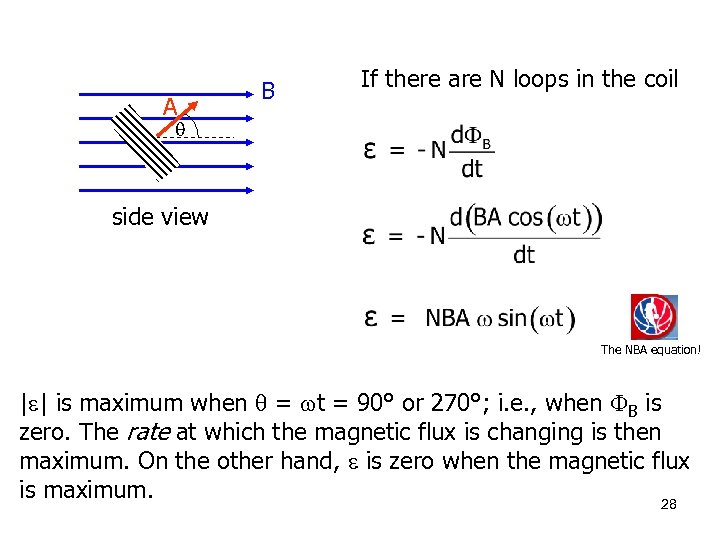A B If there are N loops in the coil side view The NBA equation! | | is maximum when = t = 90° or 270°; i. e. , when B is zero. The rate at which the magnetic flux is changing is then maximum. On the other hand, is zero when the magnetic flux is maximum. 28

emf, current and power from a generator 29

Example: the armature of a 60 Hz ac generator rotates in a 0. 15 T magnetic field. If the area of the coil is 2 x 10 -2 m 2, how many loops must the coil contain if the peak output is to be max = 170 V? 30

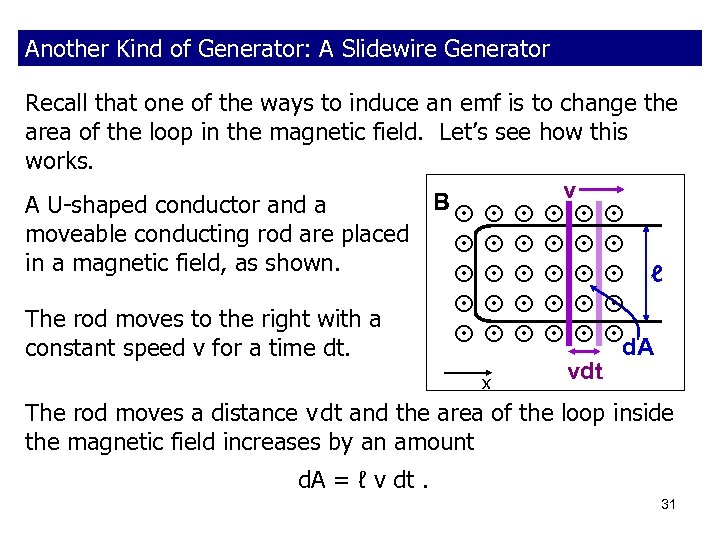Another Kind of Generator: A Slidewire Generator Recall that one of the ways to induce an emf is to change the area of the loop in the magnetic field. Let’s see how this works. B v A U-shaped conductor and a moveable conducting rod are placed in a magnetic field, as shown. ℓ The rod moves to the right with a d. A constant speed v for a time dt. vdt x The rod moves a distance v dt and the area of the loop inside the magnetic field increases by an amount d. A = ℓ v dt. 31

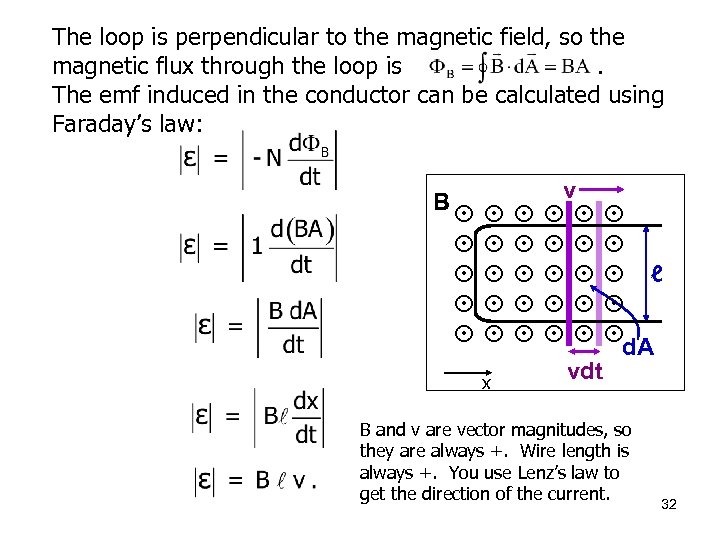The loop is perpendicular to the magnetic field, so the magnetic flux through the loop is. The emf induced in the conductor can be calculated using Faraday’s law: B x vdt ℓ d. A B and v are vector magnitudes, so they are always +. Wire length is always +. You use Lenz’s law to get the direction of the current. 32

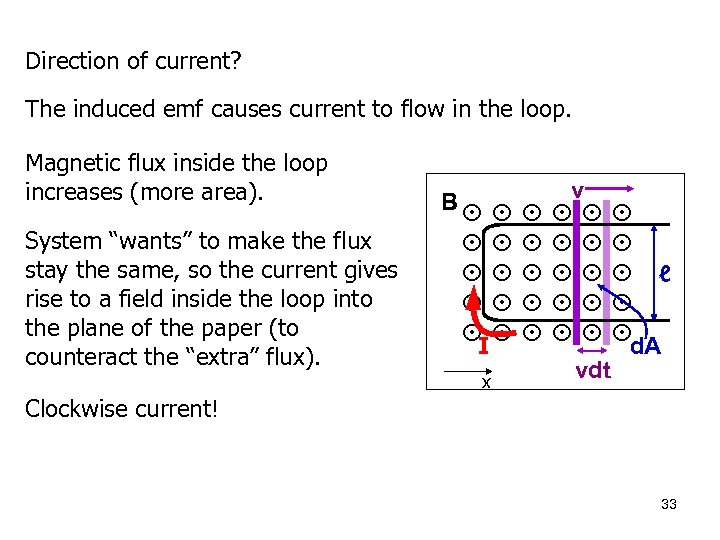Direction of current? The induced emf causes current to flow in the loop. Magnetic flux inside the loop increases (more area). System “wants” to make the flux stay the same, so the current gives rise to a field inside the loop into the plane of the paper (to counteract the “extra” flux). B I x vdt ℓ d. A Clockwise current! 33

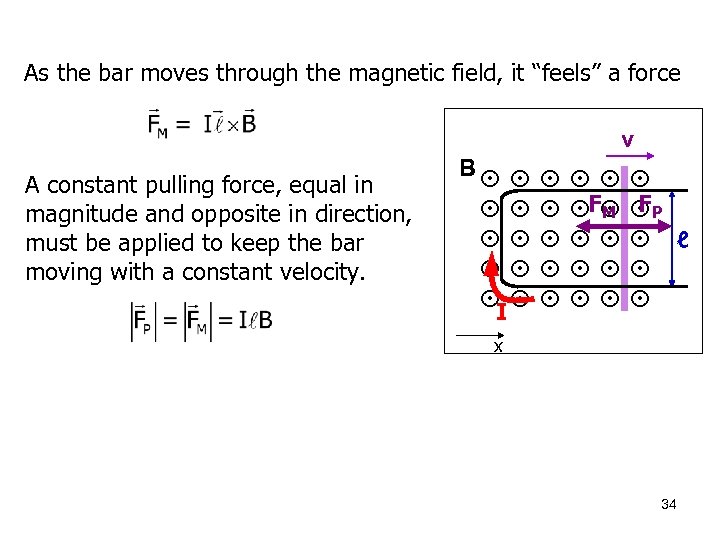As the bar moves through the magnetic field, it “feels” a force v A constant pulling force, equal in magnitude and opposite in direction, must be applied to keep the bar moving with a constant velocity. B I F M F P ℓ x 34

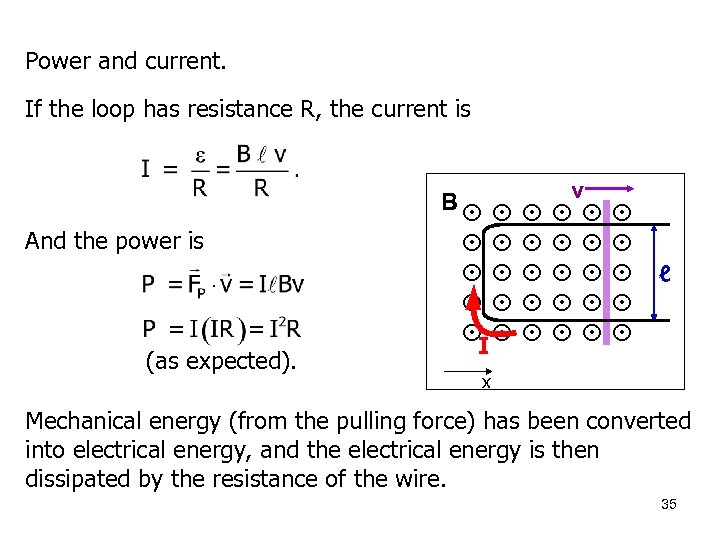Power and current. If the loop has resistance R, the current is And the power is (as expected). B I v ℓ x Mechanical energy (from the pulling force) has been converted into electrical energy, and the electrical energy is then dissipated by the resistance of the wire. 35

Today’s agendum: Motional emf. You must be able to apply Faraday’s and Lenz’s “Laws” to calculate motional emf, as well as current and power in circuits powered by motional emf. Motors and Generators (part 2). In the previous lecture, we used Faraday’s “Law” to calculate numerical values of parameters associated with generators. You must also understand conceptually how motors and generators work. Back emf. You must be able to use Lenz’s “Law” to explain back emf. 36

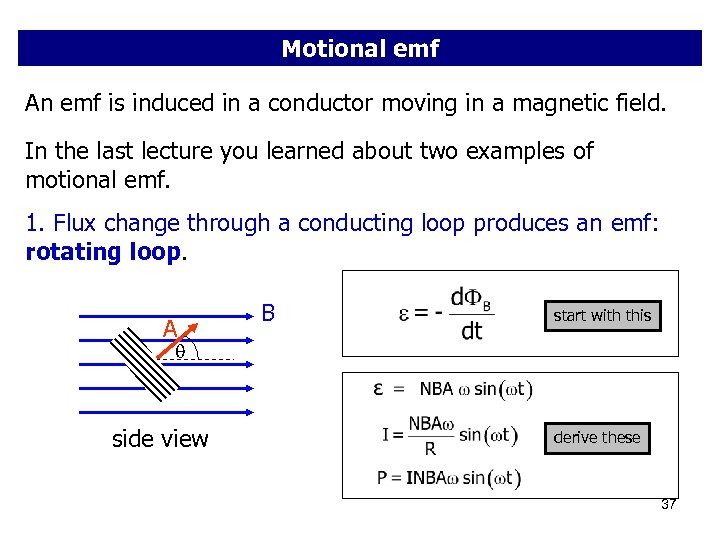Motional emf An emf is induced in a conductor moving in a magnetic field. In the last lecture you learned about two examples of motional emf. 1. Flux change through a conducting loop produces an emf: rotating loop. A B start with this side view derive these 37

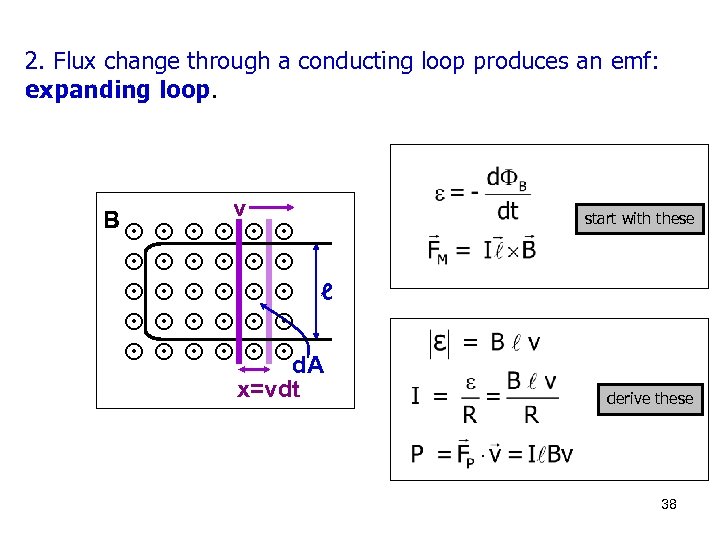2. Flux change through a conducting loop produces an emf: expanding loop. B v ℓ d. A x=vdt start with these derive these 38

Today we’ll look at two more examples of motional emf. 3. Conductor moving in a magnetic field experiences an emf: magnetic force on charged particles. B v – + start with these ℓ derive this You could also solve this using Faraday’s “Law” by constructing a “virtual” circuit using “virtual” conductors. 39

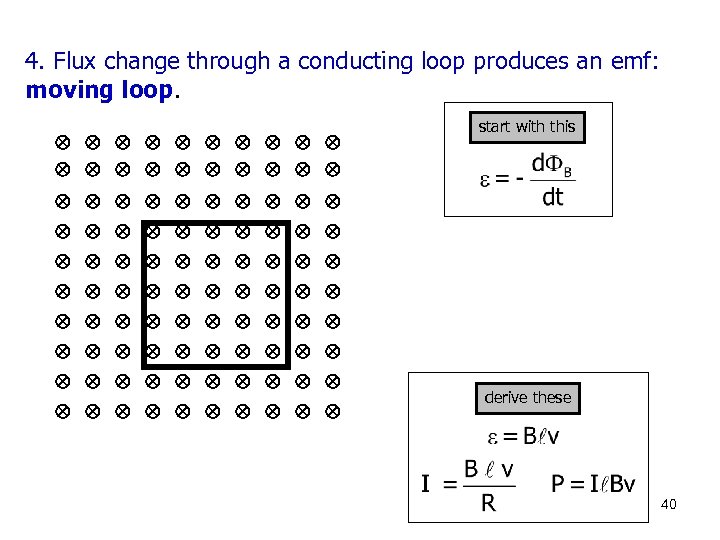4. Flux change through a conducting loop produces an emf: moving loop. start with this derive these 40

Example 3 of motional emf: moving conductor in B field. Example 4 of motional emf: flux change through conducting loop. (Entire loop is moving. ) Let’s work out these two examples now. Remember, it’s the flux change that produces the emf. Flux has no direction associated with it. However, the presence of flux is due to the presence of a magnetic field, which does have a direction, and allows us to use Lenz’s “Law” to determine the “direction” of current and emf. 41

Example 3 of motional emf: moving conductor in B field. Motional emf is the emf induced in a conductor moving in a magnetic field. If a conductor (purple bar) moves with speed v in a magnetic field, the electrons in the bar experience a force B v – + “up” ℓ The force on the electrons is “up, ” so the “top” end of the bar acquires a net – charge and the “bottom” end of the bar acquires a net + charge. 42

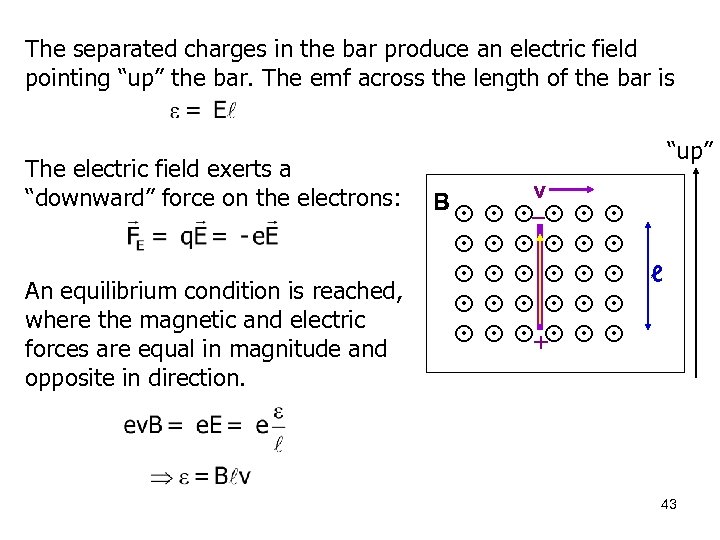The separated charges in the bar produce an electric field pointing “up” the bar. The emf across the length of the bar is The electric field exerts a “downward” force on the electrons: An equilibrium condition is reached, where the magnetic and electric forces are equal in magnitude and opposite in direction. “up” B v – + ℓ 43

Example 4 of motional emf: flux change through conducting loop. (Entire loop is moving. ) I’ll include some numbers with this example. 44

A square coil of side 5 cm contains 100 loops and is positioned perpendicular to a uniform 0. 6 T magnetic field. It is quickly and uniformly pulled from the field (moving to B) to a region where the field drops abruptly to zero. It takes 0. 10 s to remove the coil, whose resistance is 100 . 5 cm B = 0. 6 T 45

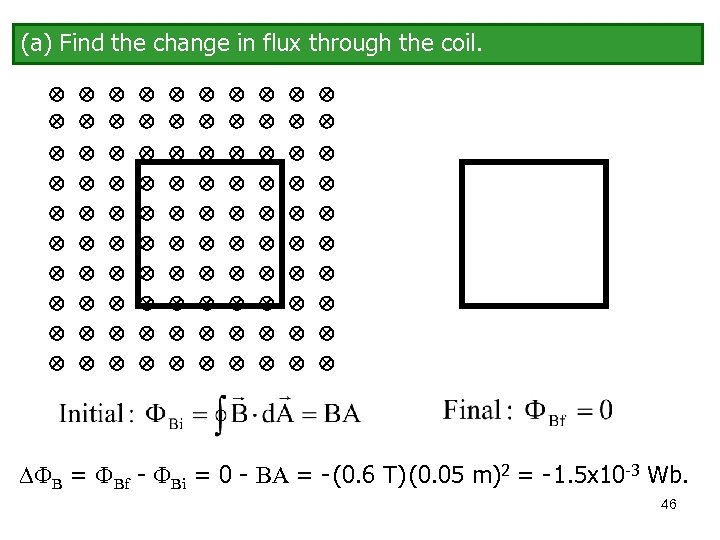(a) Find the change in flux through the coil. B = Bf - Bi = 0 - BA = - (0. 6 T) (0. 05 m)2 = - 1. 5 x 10 -3 Wb. 46

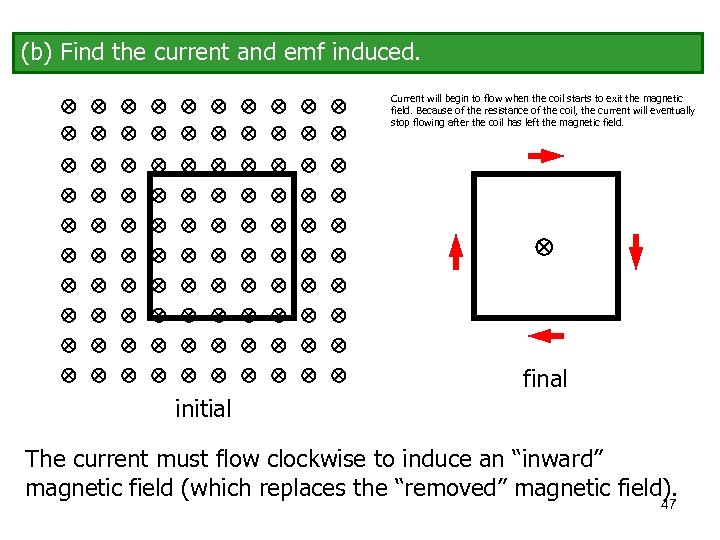(b) Find the current and emf induced. Current will begin to flow when the coil starts to exit the magnetic field. Because of the resistance of the coil, the current will eventually stop flowing after the coil has left the magnetic field. final initial The current must flow clockwise to induce an “inward” magnetic field (which replaces the “removed” magnetic field). 47

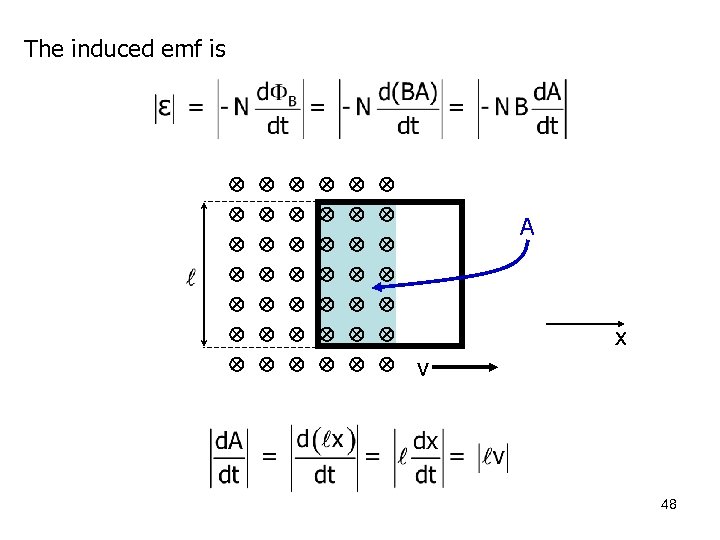The induced emf is A x v 48

“uniformly” pulled The induced current is 49

(c) How much energy is dissipated in the coil? Current flows “only*” during the time flux changes. W = P t = I 2 R t = (1. 5 x 10 -2 A)2 (100 ) (0. 1 s) = 2. 25 x 10 -3 J (d) Discuss the forces involved in this example. The loop has to be “pulled” out of the magnetic field, so there is a pulling force, which does work. The “pulling” force is opposed by a magnetic force on the current flowing in the wire. If the loop is pulled “uniformly” out of the magnetic field (no acceleration) the pulling and magnetic forces are equal in magnitude and opposite in direction. *Remember: if there were no resistance in the loop, the current would flow indefinitely. However, the resistance quickly halts the flow of current once the magnetic flux stops changing. 50

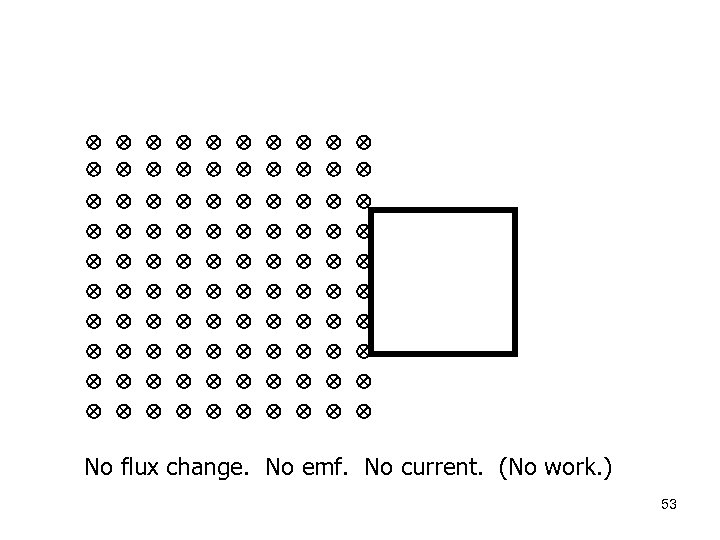
The flux change occurs only when the coil is in the process of leaving the region of magnetic field. No No flux change. emf. current. work (why? ). 51

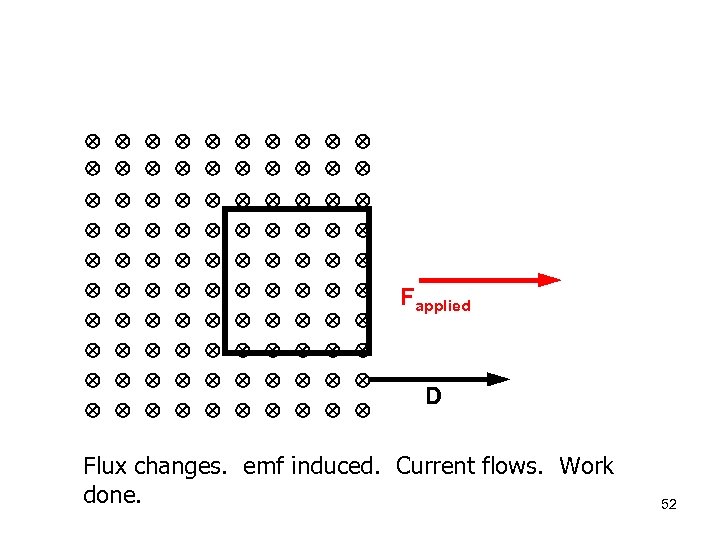Fapplied D Flux changes. emf induced. Current flows. Work done. 52

No flux change. No emf. No current. (No work. ) 53

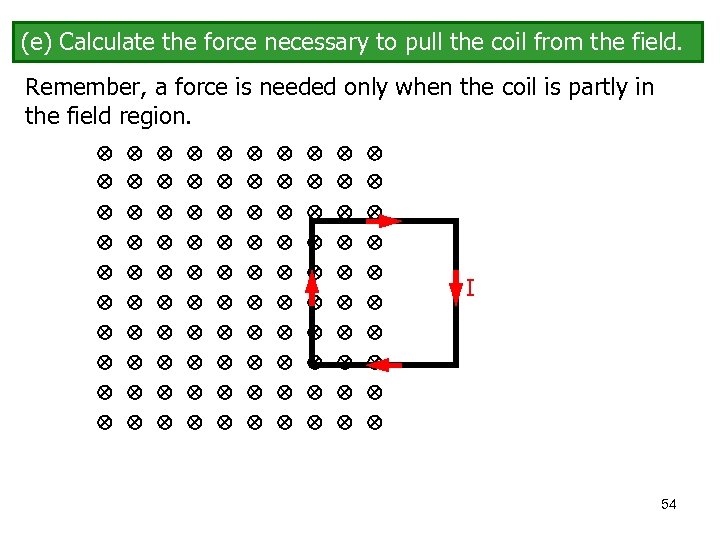(e) Calculate the force necessary to pull the coil from the field. Remember, a force is needed only when the coil is partly in the field region. I 54

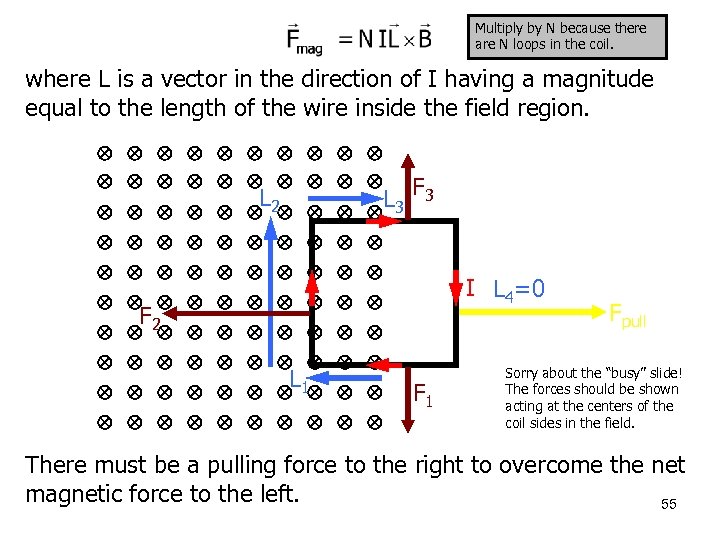Multiply by N because there are N loops in the coil. where L is a vector in the direction of I having a magnitude equal to the length of the wire inside the field region. L 3 F 3 L 2 F 2 L 1 I L 4=0 F 1 Fpull Sorry about the “busy” slide! The forces should be shown acting at the centers of the coil sides in the field. There must be a pulling force to the right to overcome the net magnetic force to the left. 55

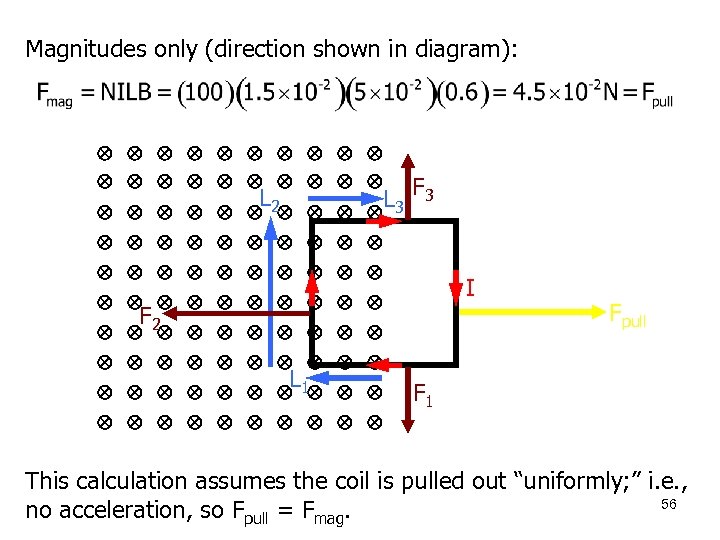Magnitudes only (direction shown in diagram): L 3 F 3 L 2 F 2 L 1 I Fpull F 1 This calculation assumes the coil is pulled out “uniformly; ” i. e. , 56 no acceleration, so Fpull = Fmag.

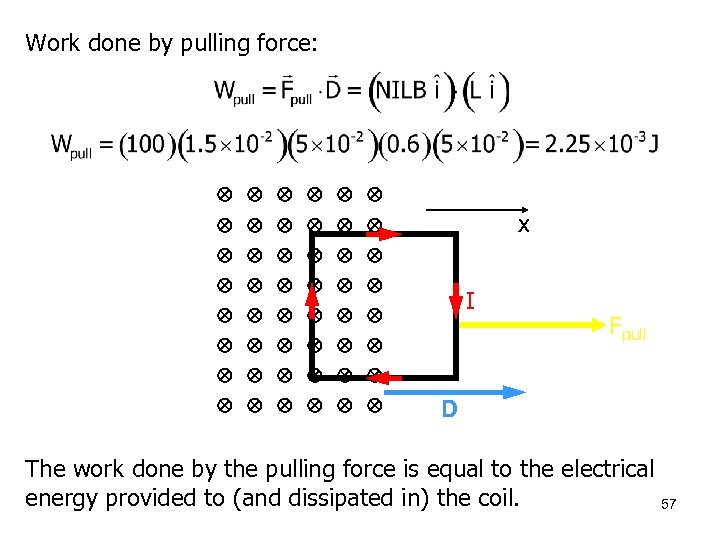Work done by pulling force: x I Fpull D The work done by the pulling force is equal to the electrical energy provided to (and dissipated in) the coil. 57

Handy Hint: Debugging Your Homemade Generator If you build a generator and it doesn’t seem to be working… European model shown. US model also available. …or if you want to test a wall socket to see if it is “live…” …simply purchase a Vilcus Plug Dactyloadapter from Think. Geek ( http: //www. thinkgeek. com/stuff/41/lebedev. shtml ) and follow the instructions. 58

Today’s agendum: Motional emf. You must be able to apply Faraday’s and Lenz’s “Laws” to calculation motional emf, as well as current and power in circuits powered by motional emf. Motors and Generators (part 2). In the previous lecture, we used Faraday’s “Law” to calculate numerical values of parameters associated with generators. You must also understand conceptually how motors and generators work. Back emf. You must be able to use Lenz’s “Law” to explain back emf. 59

electric motors and web applets Generator: source of mechanical energy rotates a current loop in a magnetic field, and mechanical energy is converted into electrical energy. Electric motor: a generator “in reverse. ” Current in loop in magnetic field gives rise to torque on loop. A dc motor animation is here. Details about ac and dc motors at hyperphysics. Other useful animations here. True Fact you didn’t know: all electrical motors operate on smoke. Every motor has the correct amount of smoke sealed inside it at the factory. If this smoke ever gets out, the motor is no longer functional. I can even provide the source of this true information. http: //www. xs 4 all. nl/~jcdverha/scijokes/2_16. html#subindex 60

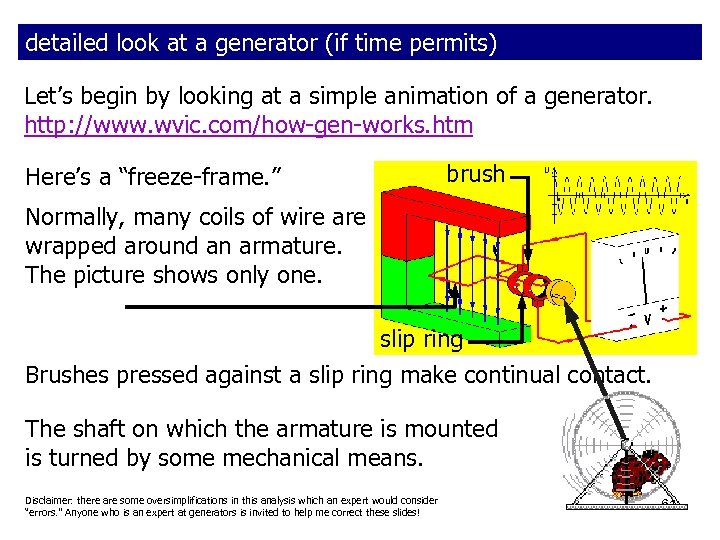detailed look at a generator (if time permits) Let’s begin by looking at a simple animation of a generator. http: //www. wvic. com/how-gen-works. htm brush Here’s a “freeze-frame. ” Normally, many coils of wire are wrapped around an armature. The picture shows only one. slip ring Brushes pressed against a slip ring make continual contact. The shaft on which the armature is mounted is turned by some mechanical means. Disclaimer: there are some oversimplifications in this analysis which an expert would consider “errors. ” Anyone who is an expert at generators is invited to help me correct these slides! 61

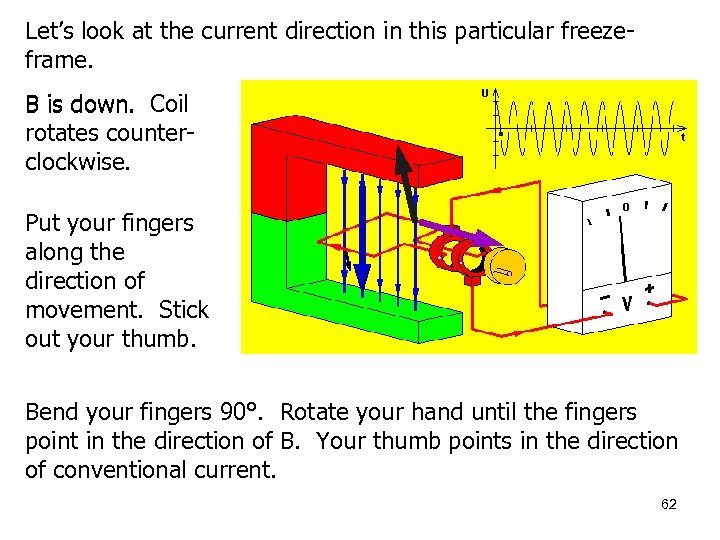Let’s look at the current direction in this particular freezeframe. B is down. Coil rotates counterclockwise. Put your fingers along the direction of movement. Stick out your thumb. Bend your fingers 90°. Rotate your hand until the fingers point in the direction of B. Your thumb points in the direction of conventional current. 62

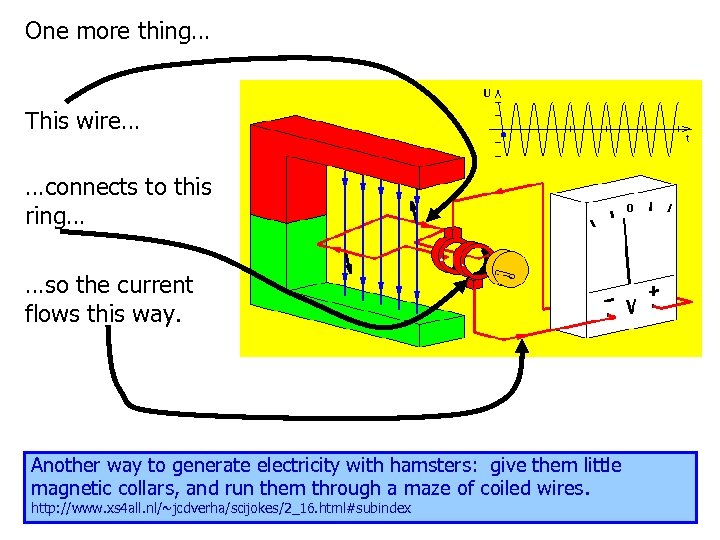One more thing… This wire… …connects to this ring… …so the current flows this way. Another way to generate electricity with hamsters: give them little magnetic collars, and run them through a maze of coiled wires. http: //www. xs 4 all. nl/~jcdverha/scijokes/2_16. html#subindex 63

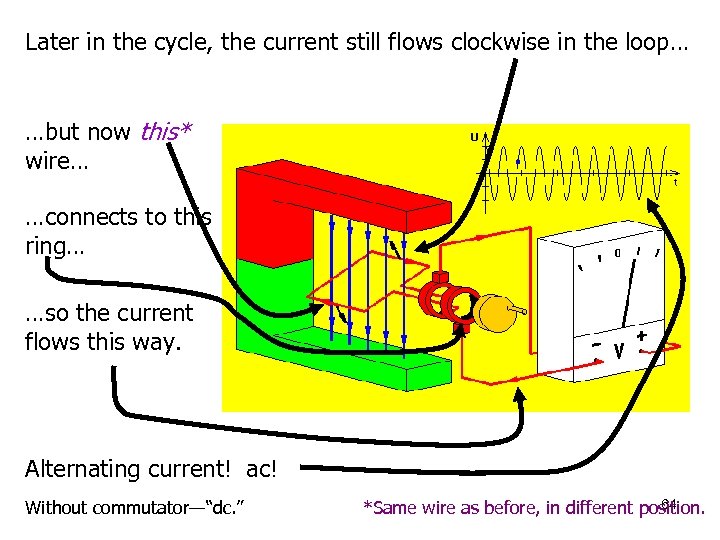Later in the cycle, the current still flows clockwise in the loop… …but now this* wire… …connects to this ring… …so the current flows this way. Alternating current! ac! Without commutator—“dc. ” 64 *Same wire as before, in different position.

Today’s agendum: Motional emf. You must be able to apply Faraday’s and Lenz’s “Laws” to calculation motional emf, as well as current and power in circuits powered by motional emf. Motors and Generators (part 2). In the previous lecture, we used Faraday’s “Law” to calculate numerical values of parameters associated with generators. You must also understand conceptually how motors and generators work. Back emf. You must be able to use Lenz’s “Law” to explain back emf. 65

back emf (also known as “counter emf”) (if time permits) A changing magnetic field in wire produces a current. A constant magnetic field does not. We saw how changing the magnetic field experienced by a coil of wire produces ac current. But the electrical current produces a magnetic field, which by Lenz’s law, opposes the change in flux which produced the current in the first place. http: //campus. murraystate. edu/tsm 118/Ch 7_4/Ch 7_4. htm 66

The effect is “like” that of friction. The counter emf is “like” friction that opposes the original change of current. Motors have many coils of wire, and thus generate a large counter emf when they are running. Good—keeps the motor from “running away. ” Bad—”robs” you of energy. 67

If your house lights dim when an appliance starts up, that’s because the appliance is drawing lots of current and not producing a counter emf. When the appliance reaches operating speed, the counter emf reduces the current flow and the lights “undim. ” Motors have design speeds their engineers expect them to run at. If the motor runs at a lower speed, there is less-thanexpected counter emf, and the motor can draw more-thanexpected current. If a motor is jammed or overloaded and slows or stops, it can draw enough current to melt the windings and burn out. Or even burn up. 68

Two brief examples (if time permits): Induced emf on an airplane wing. Blood flow measurement. 69

Example: An airplane travels 1000 km/h in a region where the earth’s field is 5 x 10 -5 T and is vertical. What is the potential difference induced between the wing tips that are 70 m apart? v 70

The electrons “pile up” on the left hand wing of the plane, leaving an excess of + charge on the right hand wing. The equation for at the bottom of slide 10 gives the potential difference. (You’d have to derive this on a test. ) + v No danger to passengers! (But I would want my airplane designers to be aware of this. ) 71

Example: Blood contains charged ions, so blood flow can be measured by applying a magnetic field and measuring the induced emf. If a blood vessel is 2 mm in diameter and a 0. 08 T magnetic field causes an induced emf of 0. 1 mv, what is the flow velocity of the blood? =Bℓv v = / (B ℓ) If B is applied to the blood vessel, then B is to v. The ions flow along the blood vessel, but the emf is induced across the blood vessel, so ℓ is the diameter of the blood vessel. v = (0. 1 x 10 -3 V) / ( (0. 08 T)(0. 2 x 10 -3 m) ) v = 0. 63 m/s 72

Today’s agendum: Induced Electric Fields. You must understand how a changing magnetic flux induces an electric field, and be able to calculate induced electric fields. Eddy Currents. You must understand how induced electric fields give rise to circulating currents called “eddy currents. ” Displacement Current and Maxwell’s Equations. Displacement currents explain how current can flow “through” a capacitor, and how a time -varying electric field can induce a magnetic field. Leftovers. Any assorted topics I need to “cover” before finishing magnetism. 73

Time-Varying Magnetic Fields and Induced Electric Fields A Changing Magnetic Flux Produces an Electric Field? This suggests that a changing magnetic flux produces an electric field. This is true not just in conductors, but any-where in space where there is a changing magnetic field. 74

The previous slide uses an equation derived specifically for the electric field between two large parallel plates. Let’s see what a more general analysis gives us. Consider the conducting loop of radius r around (but not in) a region where the magnetic field is into the page and increasing. r This could be a wire loop around the outside of a solenoid. The charged particles in the conductor are not in a magnetic field, so they experience no magnetic force. But the changing magnetic flux induces an emf around the loop. 75

The induced emf causes a counterclockwise current (charges move). But the magnetic field did not accelerate the charged particles (they aren’t in it). Therefore, there must be a tangential electric field around the loop. E E I r E E The work done moving a charged particle once around the loop is. The sign is positive because the particle’s kinetic energy increases. 76

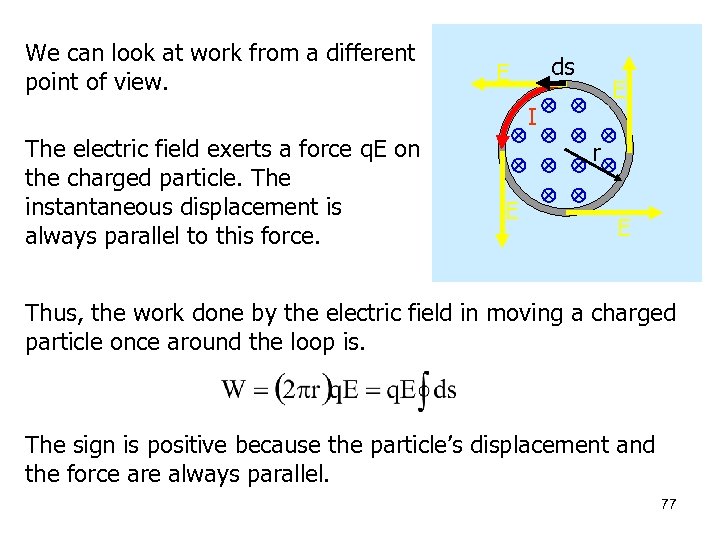We can look at work from a different point of view. ds E E I The electric field exerts a force q. E on the charged particle. The instantaneous displacement is always parallel to this force. r E E Thus, the work done by the electric field in moving a charged particle once around the loop is. The sign is positive because the particle’s displacement and the force are always parallel. 77

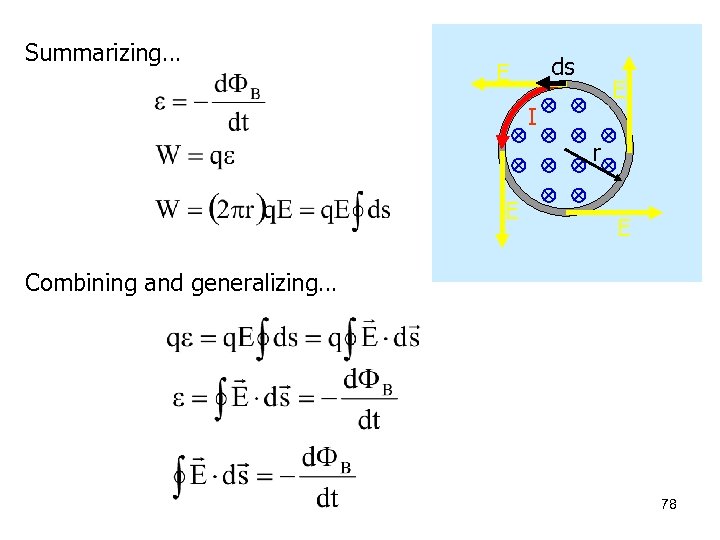Summarizing… ds E E I r E E Combining and generalizing… 78

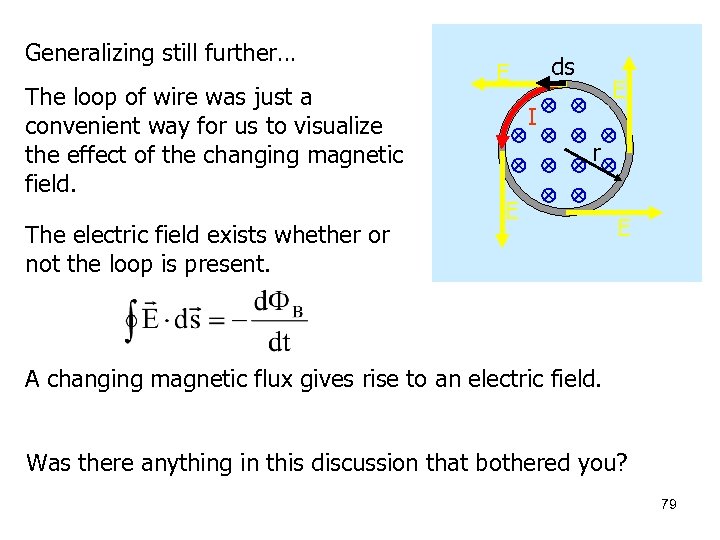Generalizing still further… The loop of wire was just a convenient way for us to visualize the effect of the changing magnetic field. The electric field exists whether or not the loop is present. ds E E I r E E A changing magnetic flux gives rise to an electric field. Was there anything in this discussion that bothered you? 79

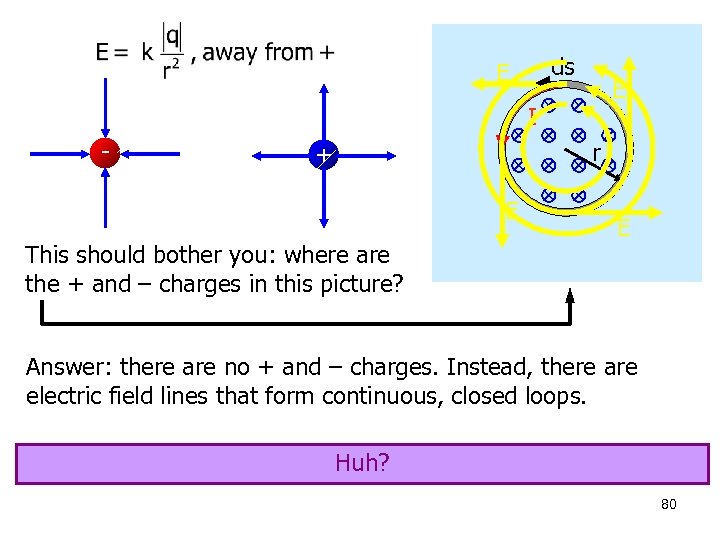ds E E I - r + E This should bother you: where are the + and – charges in this picture? E Answer: there are no + and – charges. Instead, there are electric field lines that form continuous, closed loops. Huh? 80

But wait…there’s more! A potential energy can be defined only for a conservative force. * A potential energy is a single-valued function. E If this electric field E is due to a conservative force, then the potential energy of a charged particle must be unchanged when it goes once around the loop. *The work done by the force is independent of path. 81

But the work done is I and F Work depends on the path! E r If we tried to define a potential energy, it would not be singlevalued: U is not single-valued! We can’t define a U for this E! (*%&^#!) 82

Induced Electric Fields: a summary of the key ideas A changing magnetic flux induces an electric field, as given by Faraday’s Law: This is a different kind of electric field than the one you are familiar with; it is not the electrostatic field caused by the presence of charged particles. Unlike the electrostatic electric field, this “new” electric field is nonconservative. “conservative, ” or “Coulomb” “nonconservative” 83

Stated slightly differently: we have “discovered” two different ways to generate an electric field. Coulomb Electric Field “Faraday” Electric Field Both “kinds” of electric fields are part of Maxwell’s Equations. Both “kinds” of electric fields exert forces on charged particles. The Coulomb force is conservative, the “Faraday” force is not. 84

Direction of Induced Electric Fields The direction of E is in the direction a positively charged particle would be accelerated by the changing flux. Use Lenz’s Law to determine the direction the changing flux would cause a current to flow. That is the direction of E. 85

Example A long thin solenoid has 900 turns per meter and a radius of 2. 50 cm. The current is increasing at a steady rate of 60 A/s. What is the magnitude of the induced electric field near the center of the solenoid 0. 5 cm from the axis of the solenoid? 86

Some Revolutionary Applications of Faraday’s Law Magnetic Tape Readers Phonograph Cartridges Electric Guitar Pickup Coils Ground Fault Interruptors Alternators Generators Transformers Electric Motors 87

The Big Picture You have now learned Gauss’s Law for both electricity and magnetism… and Faraday’s Law of Induction: These equations can also be written in differential form: 88

Today’s agendum: Induced Electric Fields. You must understand how a changing magnetic flux induces an electric field, and be able to calculate induced electric fields. Eddy Currents. You must understand how induced electric fields give rise to circulating currents called “eddy currents. ” Displacement Current and Maxwell’s Equations. Displacement currents explain how current can flow “through” a capacitor, and how a time -varying electric field can induce a magnetic field. Leftovers. Any assorted topics I need to “cover” before Spring Break. 89

Eddy Currents You have seen how a changing magnetic field can induce a “swirling” current in a conductor (the beginning of this lecture). If a conductor and a magnetic field are in relative motion, the magnetic force on charged particles in the conductor causes circulating currents. These currents are called “eddy currents. ” Eddy currents give rise to magnetic fields that oppose any external change in the magnetic field. 90

Eddy Currents Eddy currents are useful in generators, microphones, and roller coaster brakes (among other things). However, the I 2 R heating from eddy currents causes energy loss, so if you don’t want energy loss, you probably think eddy currents are “bad. ” 91

Conceptual Example: Induction Stove An ac current in a coil in the stove top produces a changing magnetic field at the bottom of a metal pan. The changing magnetic field gives rise to a current in the bottom of the pan. Because the pan has resistance, the current heats the pan. If the coil in the stove has low resistance it doesn’t get hot but the pan does. An insulator won’t heat up on an induction stove. Remember the controversy about cancer from power lines a few years back? Careful studies showed no harmful effect. Nevertheless, some believe induction stoves are hazardous. 92

Today’s agendum: Induced Electric Fields. You must understand how a changing magnetic flux induces an electric field, and be able to calculate induced electric fields. Eddy Currents. You must understand how induced electric fields give rise to circulating currents called “eddy currents. ” Displacement Current and Maxwell’s Equations. Displacement currents explain how current can flow “through” a capacitor, and how a time -varying electric field can induce a magnetic field. Leftovers. Any assorted topics I need to “cover” before Spring Break. 93

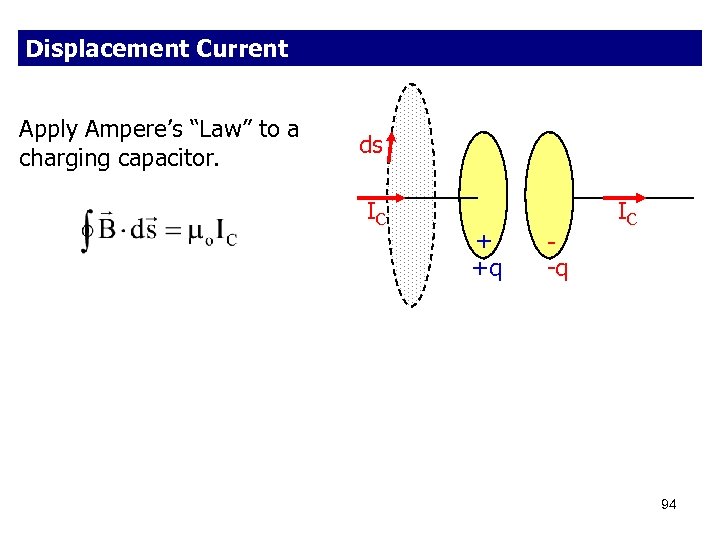Displacement Current Apply Ampere’s “Law” to a charging capacitor. ds IC + +q -q IC 94

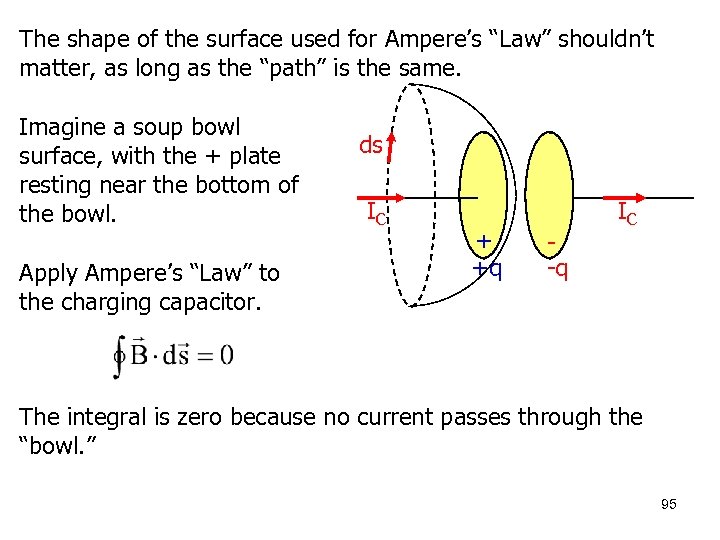The shape of the surface used for Ampere’s “Law” shouldn’t matter, as long as the “path” is the same. Imagine a soup bowl surface, with the + plate resting near the bottom of the bowl. Apply Ampere’s “Law” to the charging capacitor. ds IC + +q -q IC The integral is zero because no current passes through the “bowl. ” 95

Hold it right there pal! You can’t have it both ways. Which is it that you want? Evidently, our understanding is incomplete. 96

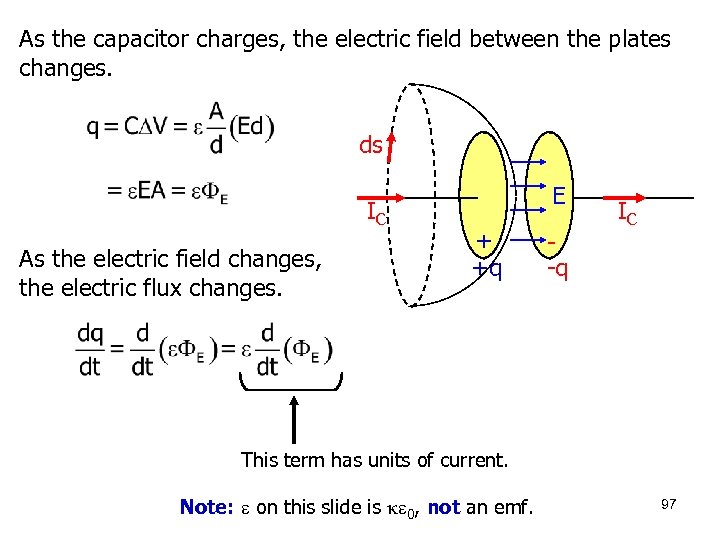As the capacitor charges, the electric field between the plates changes. ds IC As the electric field changes, the electric flux changes. E + +q -q IC This term has units of current. Note: on this slide is 0, not an emf. 97

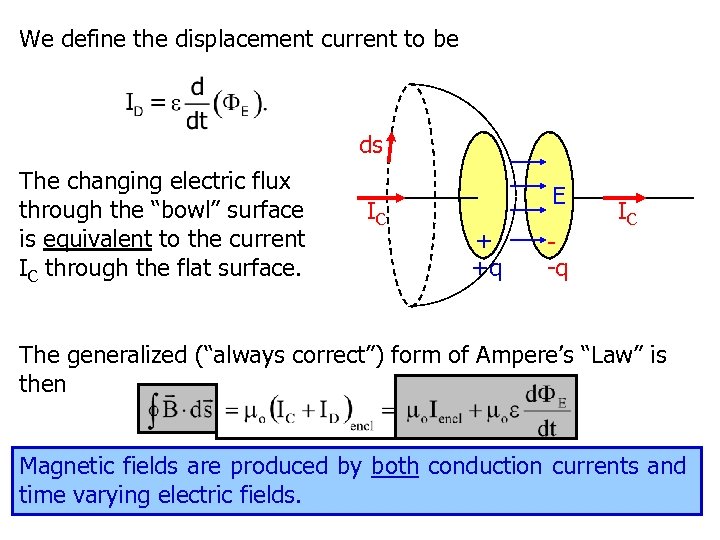We define the displacement current to be ds The changing electric flux through the “bowl” surface is equivalent to the current IC through the flat surface. IC E + +q -q IC The generalized (“always correct”) form of Ampere’s “Law” is then Magnetic fields are produced by both conduction currents and time varying electric fields. 98

The “stuff” inside the gray boxes is a new starting equation and serves as your official starting equation for the displacement current ID. In a vacuum, replace with 0. 99

The Big Picture You have now learned Gauss’s “Law” for both electricity and magnetism, Faraday’s “Law” of Induction, and the generalized form of Ampere’s “Law”: These equations can also be written in differential form: 100

Today’s agendum: Induced Electric Fields. You must understand how a changing magnetic flux induces an electric field, and be able to calculate induced electric fields. Eddy Currents. You must understand how induced electric fields give rise to circulating currents called “eddy currents. ” Displacement Current and Maxwell’s Equations. Displacement currents explain how current can flow “through” a capacitor, and how a time -varying electric field can induce a magnetic field. Leftovers. Any assorted topics I need to “cover” before Spring Break. 101

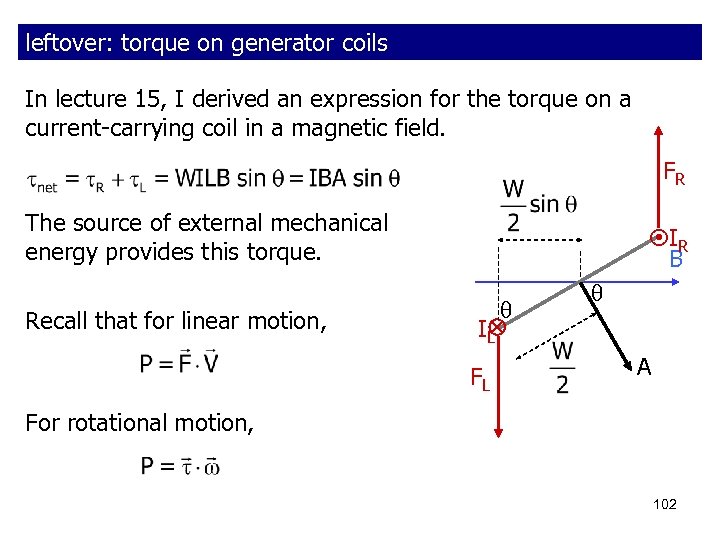leftover: torque on generator coils In lecture 15, I derived an expression for the torque on a current-carrying coil in a magnetic field. FR The source of external mechanical energy provides this torque. Recall that for linear motion, IR B IL FL A For rotational motion, 102

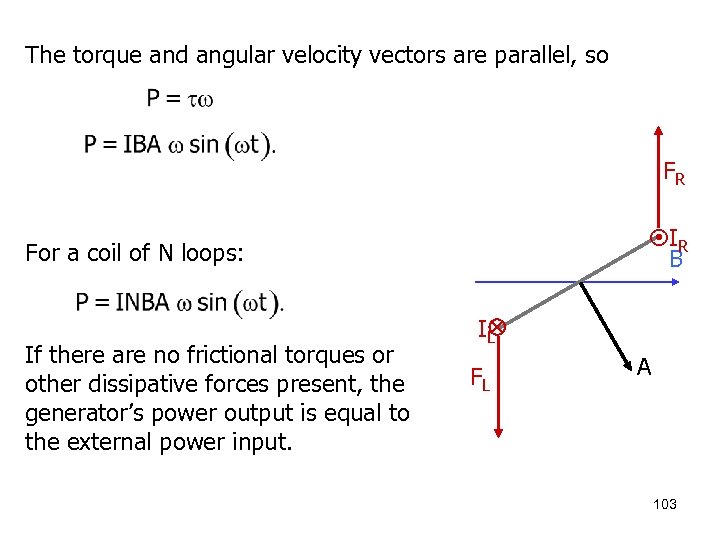The torque and angular velocity vectors are parallel, so FR IR B For a coil of N loops: If there are no frictional torques or other dissipative forces present, the generator’s power output is equal to the external power input. IL FL A 103