
Точность САУ

План 1 Общие положения 2 Понятие о типовых режимах САУ 3 Теорема о предельном значении оригинала и методика определения установившихся ошибок 4 Ошибки статических и астатических САУ в типовых режимах 5 Ошибки САУ при произвольных входных сигналах (коэффициенты ошибок) 6 Методы повышения точности САУ

1 Общие положения Точность является важнейшим критерием качества систем. В настоящее время практически все многочисленные элементы любых технических систем изготавливаются автоматически т. е. с помощью САУ. Таким образом точность САУ определяет качество продукции, товаров, их надежность, энергопотребление, долговечность и т. д. и т. п.

2 Понятие о типовых режимах САУ Точность САУ принято оценивать по величине ошибок в типовых режимах. Типовыми называются режимы просто описываемые математически и имеющие четкий физический смысл. К ним относятся: - режим покоя, когда х(t)=const; - режим линейно-нарастающих сигналов, когда х(t)=a*t, где а=const; - режим гармонических входных сигналов, когда х(t)=A*sinωt.
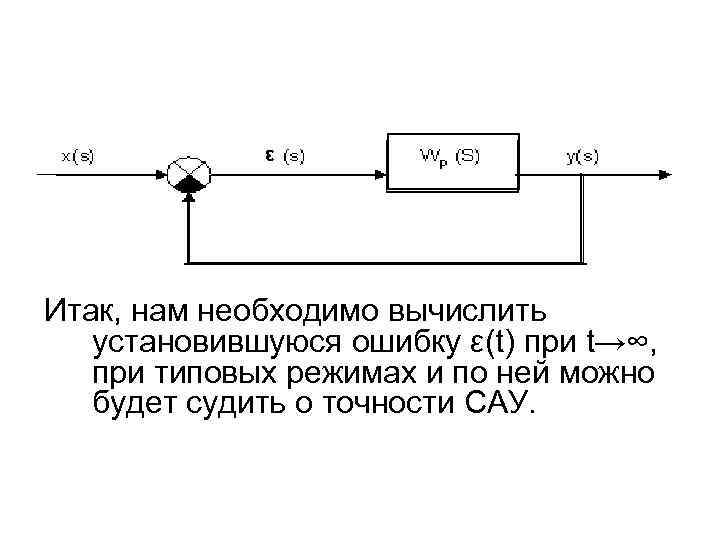
ε Итак, нам необходимо вычислить установившуюся ошибку ε(t) при t→∞, при типовых режимах и по ней можно будет судить о точности САУ.

3 Теорема о предельном значении оригинала и методика определения установившихся ошибок Сформулируем для этого теорему о предельном значении оригинала: lim. X(t)=lim. X(s), t→ ∞ s→ 0 т. е. предел оригинала при t→∞ равен пределу изображения по Лапласу при s→ 0.

Передаточная функция САУ по ошибке: Итак, чтобы определить установившуюся (при t→ ∞) ошибку САУ нужно: - Найти x(s) зная x(t) - Определить Fε(s) - Найти ε(s)= X(s) * Fε (s) - Определить εуст= lim ε(s) S→ 0

4 Ошибки статических и астатических САУ в типовых режимах Рассмотрим ошибки САУ в типовых режимах: 1. Ошибка САУ в покое (статическая ошибка) X(t)=X 0=const X(s)=X 0 Пусть - статическая САУ, поскольку в знаменателе нет множителя S, т. е. интегрирующего элемента в системе

По теореме о предельном значении аргумента (1) Подставляя Wp(s) в (1) получим:
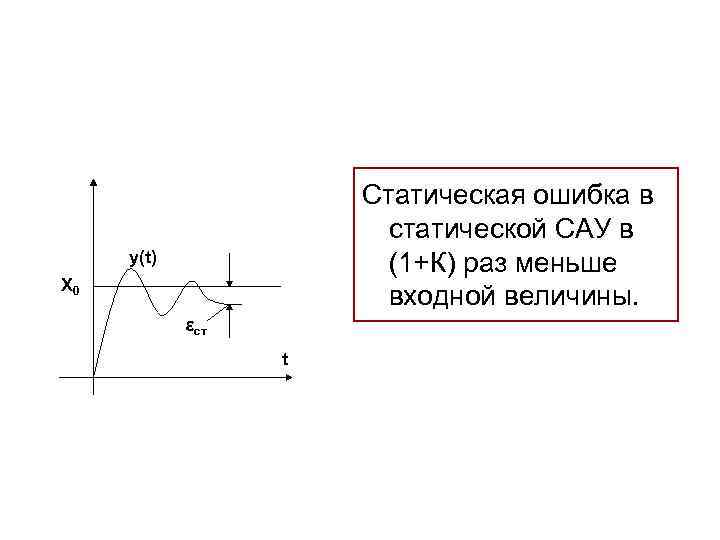
Статическая ошибка в статической САУ в (1+К) раз меньше входной величины. y(t) X 0 εст t

Пусть теперь - астатическая САУ (есть интегратор, т. е. множитель S в знаменателе передаточной функции)
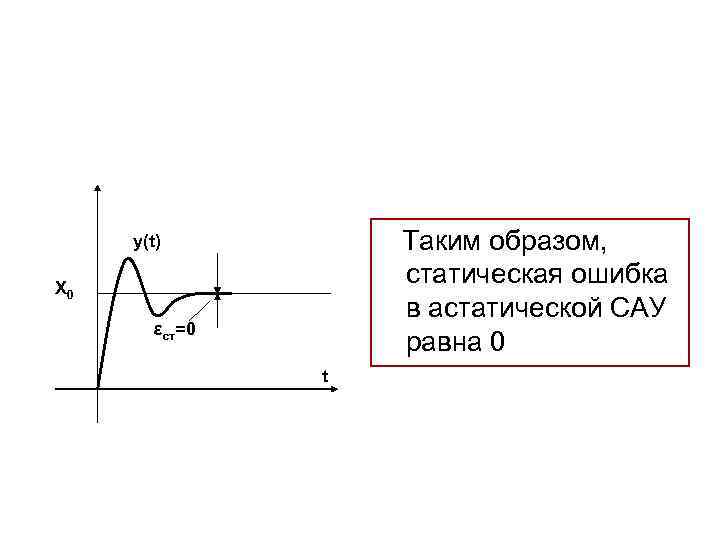
Таким образом, статическая ошибка в астатической САУ равна 0 y(t) X 0 εст=0 t

2. Второй типовой режим - движение с постоянной скоростью (скоростная ошибка) x(t)=at a=cost Пусть: - статическая САУ Тогда:
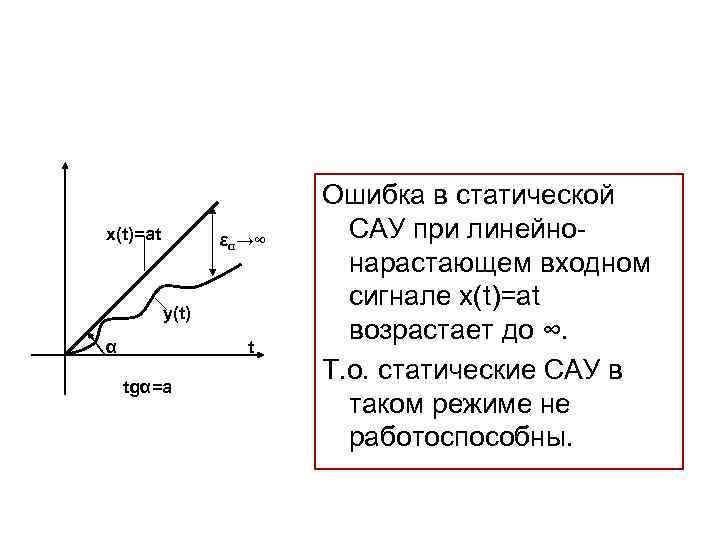
x(t)=at εα→∞ y(t) α t tgα=a Ошибка в статической САУ при линейнонарастающем входном сигнале x(t)=at возрастает до ∞. Т. о. статические САУ в таком режиме не работоспособны.

Пусть теперь - астатическая САУ Тогда
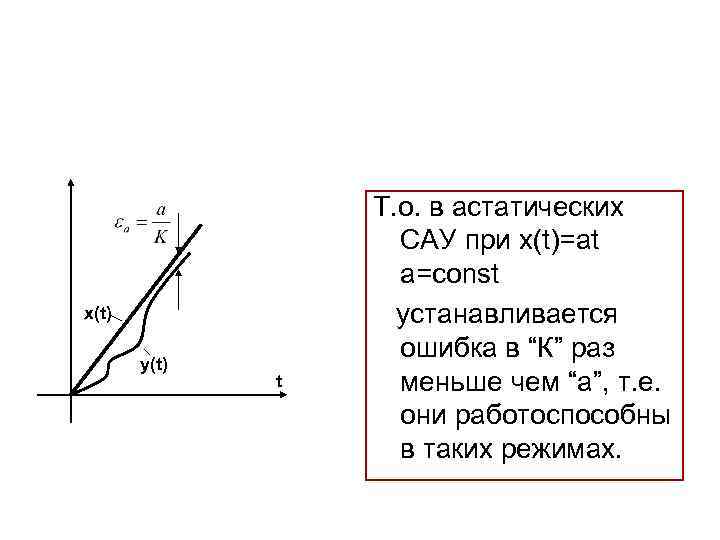
x(t) y(t) t Т. о. в астатических САУ при x(t)=at a=const устанавливается ошибка в “К” раз меньше чем “a”, т. е. они работоспособны в таких режимах.
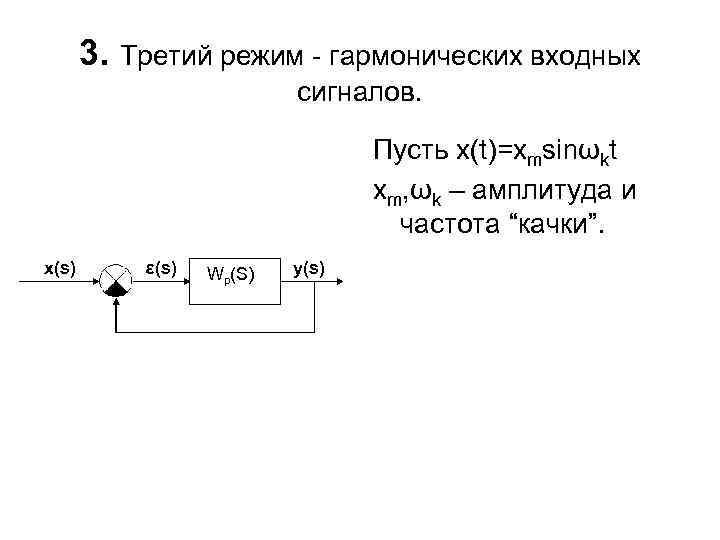
3. Третий режим - гармонических входных сигналов. Пусть x(t)=xmsinωkt xm, ωk – амплитуда и частота “качки”. x(s) ε(s) Wp(S) y(s)

Определим амплитуду εm ошибки САУ в этом режиме. Для этого найдем: - ПФ САУ по ошибке Подставим S=jωk (1)

Выражение (1) справедливо и для амплитуд, т. е. Откуда следует: (2) Ак 20 lg xm L(ω) Прологарифмируем (2): em ω ω=ωk Ак – контрольная точка (3)

Из (3) следует, что САУ будет иметь амплитуду ошибки не более допустимой εдоп, если

Т. о. чтобы ошибка САУ в гармоническом режиме не превышала допустимой εдоп необходимо: 1. Определить положение контрольной точки Ак с координатами: ω=ωк и 2. Обеспечить прохождение L(ω) выше контрольной точки Ак
5 Ошибки САУ при произвольных входных сигналах (коэффициенты ошибок) Пусть на вход САУ действует сигнал x(t) произвольной формы. Чтобы определить ошибку ε(t) в этом случае найдем вначале ее изображение. x(s) ε(s) Wp(S) y(s)

Поскольку: (1) То: (2) Разложим далее Fε(s) по возрастающим степеням S в ряд, тогда (2) можно записать в виде: (3)

При нулевых начальных условиях и переходя в (3) к оригиналам можно записать (4) Величины С 0, С 1, С 2 … называются коэффициентами ошибок САУ.

Чтобы определить ошибку САУ при произвольной форме входного сигнала x(t) необходимо: 1. Определить передаточную функцию САУ по ошибке Fε(s); 2. Разложить в ряд Fε(s) путем деления ее числителя на знаменатель и найти коэффициенты С 0, С 1, С 2 …; 3. Подставить коэффициенты ошибок в (4) и найти установившуюся ошибку ε(t).

Пример Найти ошибку в САУ при: Если:

Решение: 1. Найдем

2. Разложим (1) в степенной ряд путем деления числителя на знаменатель - -

Ограничимся первыми тремя членами ряда, т. к. входной сигнал X(t) имеет лишь три не нулевых первых производных.

3. Итак: (5) Сопоставляя (5) и (4) имеем коэффициенты ошибок: С 0=0 (6)

4. Определим далее производные от X(t): (7)

5. Подставляя коэффициенты С 0, С 1, С 2… и производные (7) в (4) получим: Т. е. ошибка с течением времени будет нарастать до ∞ из-за члена “bt”.

6 Методы повышения точности САУ Анализируя выражения для коэффициентов ошибок отметим, что: 1. Все коэффициенты обратнопропорциональны коэффициенту К – усиления системы; 2. Чем выше порядок астатизма “v” тем большее количество первых коэффициентов ошибок равны 0

ВНИМАНИЕ Порядок астатизма “v” определяется числом интегрирующих звеньев в контуре системы. Формально “v” равно показателю степени множителя S в знаменателе передаточной функции wp.

1. Первый способ повышения точности САУ – увеличение К Т. о. самым универсальным способом повышения точности САУ являются увеличение коэффициента К усиления системы. При этом все коэффициенты ошибок уменьшаются, а это означает, что система во всех режимах работы будет иметь меньшие ошибки. Однако этот способ снижает запасы устойчивости системы и рано или поздно приводит к полной потере устойчивости. Это можно показать на примере критерия Найквиста.
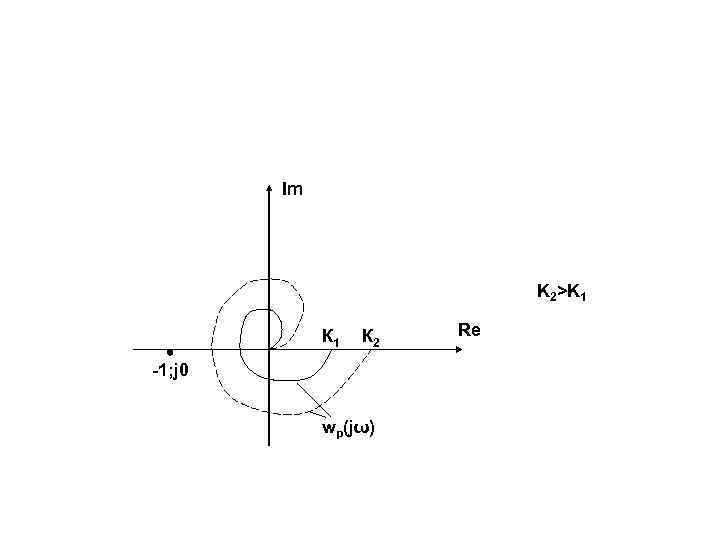
Im K 2>K 1 К 2 -1; j 0 wp(jω) Re

2. Способ повышения точности САУ – путем увеличения астатизма “v” Этот способ исключает первые коэффициенты в ряду ошибок. Действительно: v=0 (статическая САУ) Все коэффициенты не равны 0, т. е. с0≠ 0 с1≠ 0 с2≠ 0 …, т. е. статическая система в любых режимах работы, в т. ч. и в покое будет иметь ошибки

v=1 (астатическая САУ с астатизмом первого порядка) с0=0 с1≠ 0 с2≠ 0 …, т. е. такая система не будет иметь ошибки в режиме покоя. v=2 (астатическая САУ с астатизмом второго порядка) с0=0 с1=0 с2≠ 0 с3≠ 0 …, такая система не будет иметь ошибок не только в режиме покоя, но и при линейнонарастающем сигнале
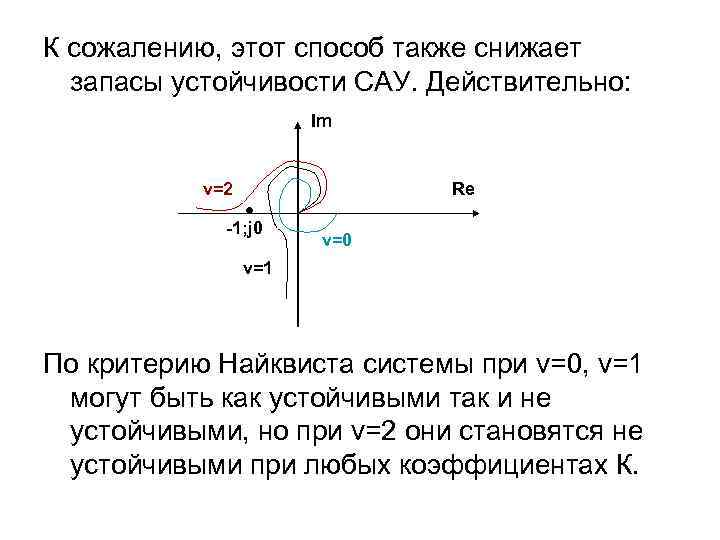
К сожалению, этот способ также снижает запасы устойчивости САУ. Действительно: Im v=2 Re -1; j 0 v=1 По критерию Найквиста системы при v=0, v=1 могут быть как устойчивыми так и не устойчивыми, но при v=2 они становятся не устойчивыми при любых коэффициентах К.
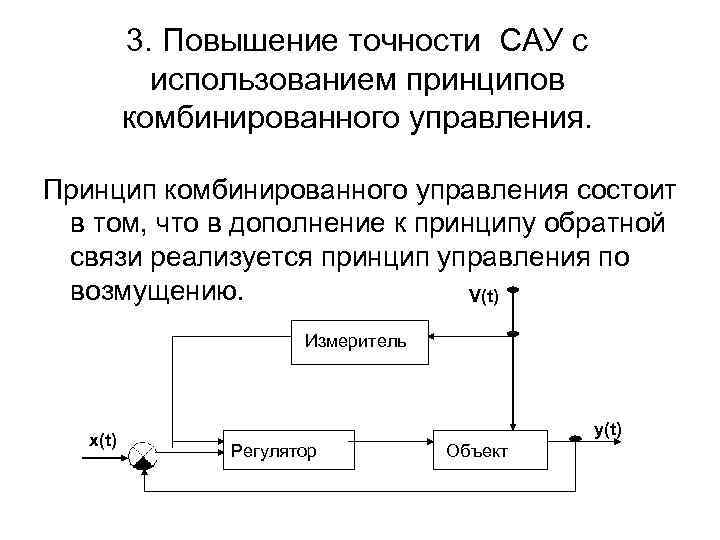
3. Повышение точности САУ с использованием принципов комбинированного управления. Принцип комбинированного управления состоит в том, что в дополнение к принципу обратной связи реализуется принцип управления по возмущению. V(t) Измеритель x(t) y(t) Регулятор Объект

Здесь сочетается (комбинируются) оба названных принципа: - Управление по возмущению (за счет измерения возмущения v(t) и выработки дополнительного управляющего сигнала компенсирующего действия возмущения); - Управление по отклонению или принцип обратной связи реализуется за счет главной отрицательной обратной связи и сигнала рассогласования и регулятора.
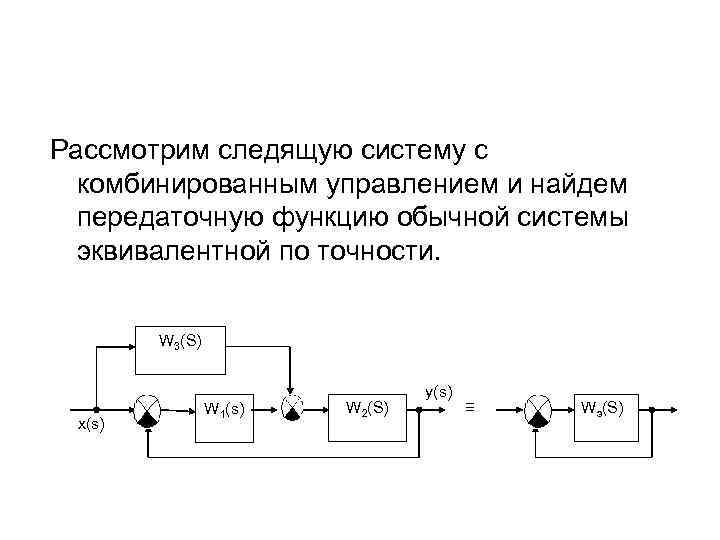
Рассмотрим следящую систему с комбинированным управлением и найдем передаточную функцию обычной системы эквивалентной по точности. W 3(S) x(s) W 1(s) W 2(S) y(s) ≡ Wэ(S)

Для этого приравняем их передаточные функции. (1)

Из (1) после некоторых преобразований можно получить: (2) Как видно из последнего выражения, при: (3) wэ(s)=∞ Условие (3) называется условием полной инвариантности.

Это означает, что ошибка рассматриваемой комбинированной следящей системы будет равна 0 в любых режимах работы поскольку:

Достоинство принципа комбинированного управления в том, что он не изменяет (не ухудшает) устойчивости и качества переходных процессов. Однако, реализовать точно условие полной инвариантности практически невозможно.

ПРИМЕР Пусть: Найдем:
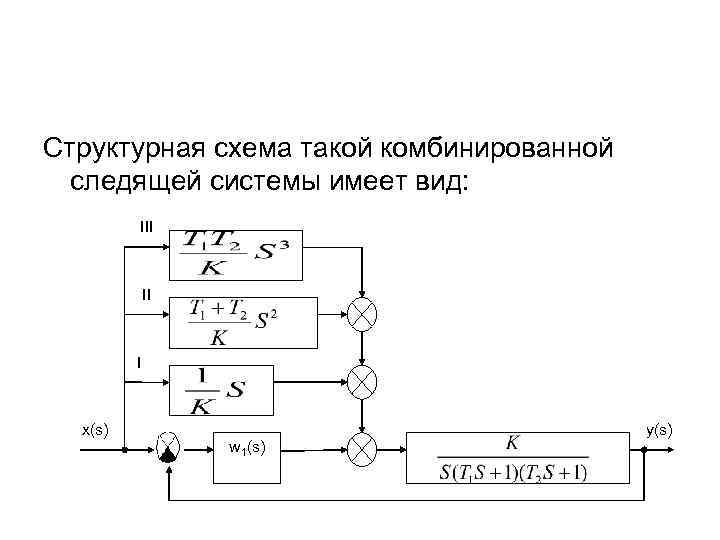
Структурная схема такой комбинированной следящей системы имеет вид: III II I x(s) w 1(s) y(s)

Итак, чтобы точно реализовать условие полной инвариантности в нашем примере необходимо: • реализовать канал I (тахогенератор) • реализовать канал II (это 2 -ая производная от угла) • реализовать канал III (это 3 -ая производная от угла) Точно это сделать практически нельзя. Кроме того, в реальных САУ имеется множество нелинейностей, которые мы не учитывали при выводе условия полной инвариантности. Поэтому часто используют частично-инвариантные САУ, т. е. САУ не имеющие ошибок лишь в некоторых режимах.