Точечная решетка на плоскости и в пространстве

Точечная решетка на плоскости и в пространстве

• Из квадратного листа бумаги в клетку, содержащего целое число клеток, вырезали квадрат, содержащий целое число клеток так, что осталось 124 клетки. Сколько клеток мог содержать первоначальный лист бумаги?

• Выпуклая фигура имеет площадь S и полупериметр p. Докажите, что если S > np для некоторого натурального n, то Ф содержит по крайней мере n целочисленных точек.

• На клетчатой бумаге нарисован прямоугольник, стороны которого образуют углы в 45 o с линиями сетки, а вершины не лежат на линиях сетки. Может ли каждую сторону прямоугольника пересекать нечетное число линий сетки?

• В пространстве с декартовой системой координат дан прямоугольный параллелепипед с длинами ребер равными √а, √ b, √с, где числа a ≤ b ≤ c — натуральны, вершины которого имеют целочисленные координаты. Его объем равен 2011. Докажите, что ребра параллелепипеда параллельны координатным осям.

• На клетчатой бумаге выбраны три точки A, B, C, находящиеся в вершинах клеток. Докажите, что если треугольник ABC остроугольный, то внутри или на сторонах его есть по крайней мере еще одна вершина клетки.

• В узлах клетчатой плоскости отмечено 5 точек. Доказать, что есть две из них, середина отрезка между которыми тоже попадает в узел.

• В квадрате 4× 4 нарисовано 15 точек Доказать, что из него можно вырезать квадратик 1× 1, не содержащий внутри себя точек.

• На прямоугольном листе клетчатой бумаги размером m×n клеток расположено несколько квадратов, стороны которых идут по вертикальным и горизонтальным линиям бумаги. Известно, что никакие два квадрата не совпадают и никакой квадрат не содержит внутри себя другой квадрат. Каково наибольшее число таких квадратов?

Многоугольники и многогранники на решетках

Проверить существует ли треугольник с вершинами в узлах сетки А(18, 0), В(0, 24), C(0, 0), у которого центры вписанной и описанной окружностей лежат в узлах сетки? Определить вид треугольника.

В пространстве расположен выпуклый многогранник, все вершины которого находятся в целых точках. Других целых точек внутри, на гранях и на ребрах нет. (Целой называется точка, все три координаты которой — целые числа. ) Доказать, что число вершин многогранника не превосходит восьми.

• На бумаге "в клеточку" нарисован выпуклый многоугольник, так что все его вершины находятся в вершинах клеток и ни одна из его сторон не идёт по вертикали или горизонтали. Докажите, что сумма длин вертикальных отрезков линий сетки, заключённых внутри многоугольника, равна сумме длин горизонтальных отрезков линий сетки внутри многоугольника.

Тангенсы углов треугольника – натуральные числа. Чему они могут быть равны?

Две знаменитые формулы: формула Пика и формула Эйлера

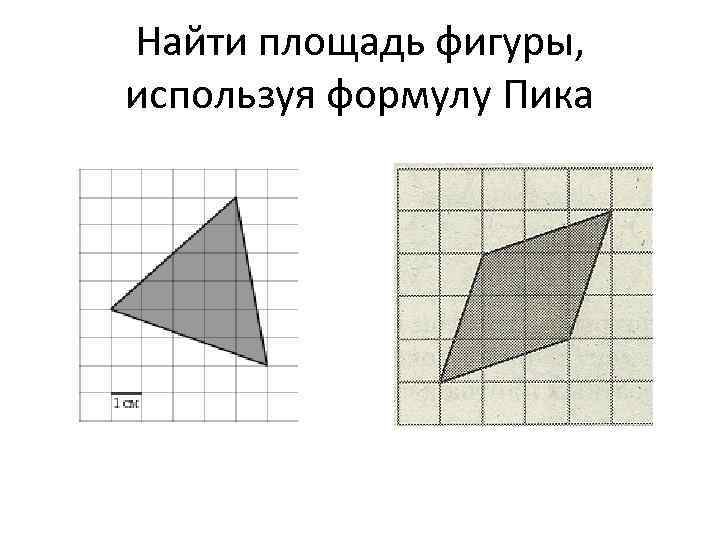Найти площадь фигуры, используя формулу Пика

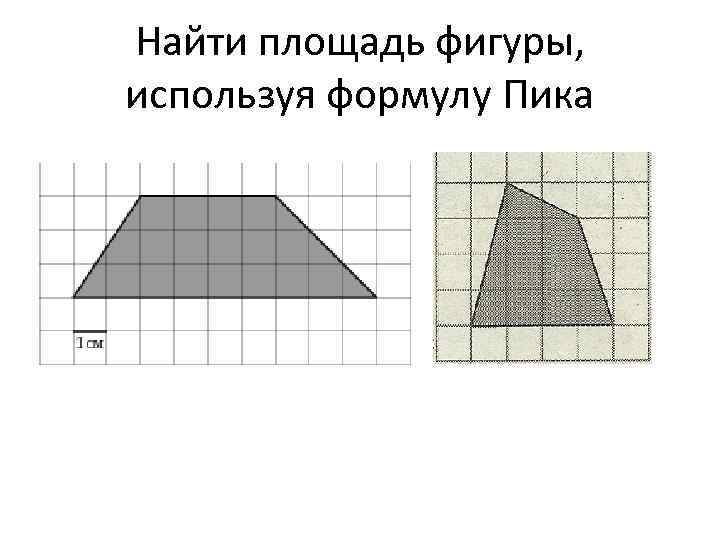Найти площадь фигуры, используя формулу Пика

Вершины треугольника ABC расположены в узлах целочисленной решетки, причем на его сторонах других узлов нет, а внутри его есть ровно один узел O. Докажите, что O — точка пересечения медиан треугольника ABC.

Докажите, что квадрат со стороной n не может накрыть более (n + 1)2 точек целочисленной решётки.