Типовая задача 1 Имеются следующие данные о

Типовая задача № 1 Имеются следующие данные о возрасте студентов заочников группе: 35, 30, 33, 25, 29, 24, 40, 36, 34, 32, 26, 25, 37, 41, 30, 27, 20, 32, 42, 38, 31, 28, 22, 33, 45, 38, 33, 29, 26. Используя данные, составьте: ранжированный ряд ( в порядке возрастания); интервальный ряд распределения. По данным типовой задачи 1 построить столбиковую диаграмму распределения студентов по возрасту. Для этого необходимо выбрать прямоугольную систему координат, где по оси абсцисс (x) откладываем возраст студентов, а по оси ординат (y) – число студентов в группе. После чего строим столбиковую диаграмму распределения студентов по возрасту в выбранном масштабе.

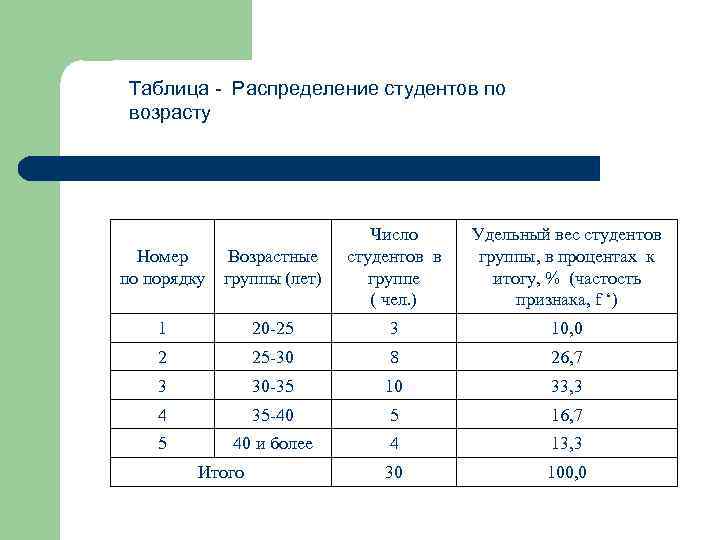Таблица - Распределение студентов по возрасту Номер по порядку Возрастные группы (лет) Число студентов в группе ( чел. ) 1 20 -25 3 10, 0 2 25 -30 8 26, 7 3 30 -35 10 33, 3 4 35 -40 5 16, 7 5 40 и более 4 13, 3 30 100, 0 Итого Удельный вес студентов группы, в процентах к итогу, % (частость признака, f ‘)

Типовая задача № 2 Имеются следующие данные по группе магазинов по размеру товарооборота, представленные в таблице 1. Провести перераспределение магазинов по размеру товарооборота. По данным типовой задачи 2 построить диаграмму распределения магазинов по размеру товарооборота за 4 квартал.

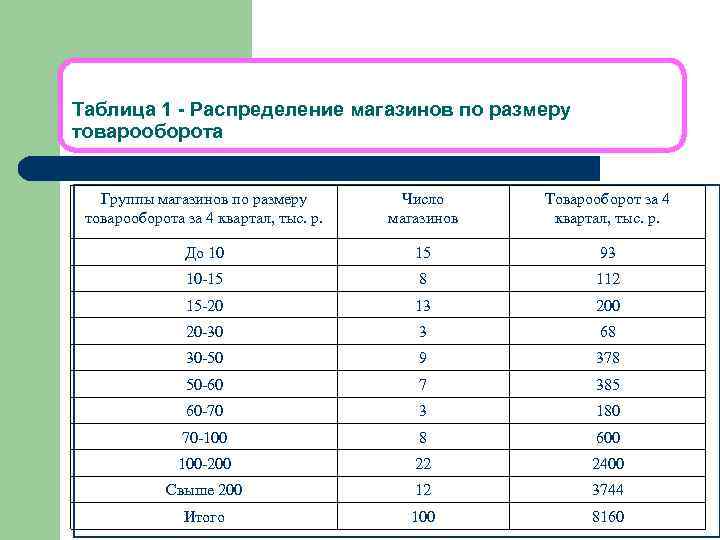Таблица 1 - Распределение магазинов по размеру товарооборота Группы магазинов по размеру товарооборота за 4 квартал, тыс. р. Число магазинов Товарооборот за 4 квартал, тыс. р. До 10 15 93 10 -15 8 112 15 -20 13 200 20 -30 3 68 30 -50 9 378 50 -60 7 385 60 -70 3 180 70 -100 8 600 100 -200 22 2400 Свыше 200 12 3744 Итого 100 8160

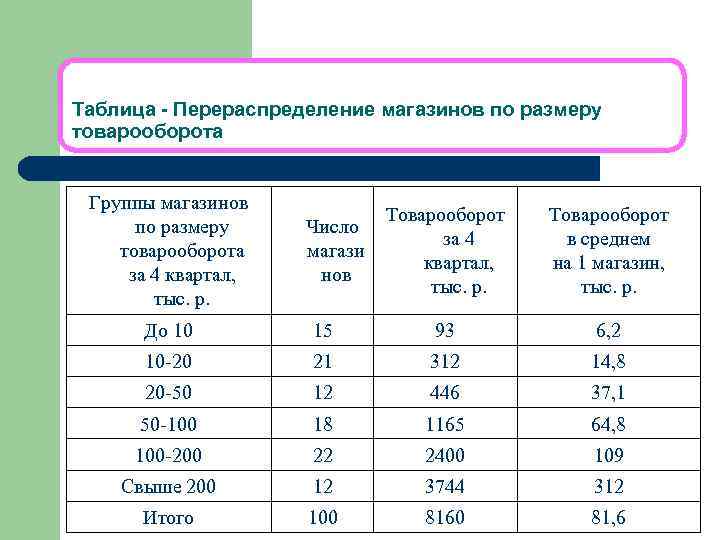Таблица - Перераспределение магазинов по размеру товарооборота Группы магазинов по размеру товарооборота за 4 квартал, тыс. р. Число магази нов Товарооборот за 4 квартал, тыс. р. Товарооборот в среднем на 1 магазин, тыс. р. До 10 15 93 6, 2 10 -20 21 312 14, 8 20 -50 12 446 37, 1 50 -100 18 1165 64, 8 100 -200 22 2400 109 Свыше 200 12 3744 312 Итого 100 8160 81, 6

Типовая задача № 3 Определить: 1) Отношение численности работников строительства и транспорта к численности работников промышленности, укажите вид относительной величины. 2) Динамику численности работников по отраслям экономики и в целом. Имеются данные в таблице 2 о среднегодовой численности рабочих и служащих по отраслям экономики ( тыс. чел. ):

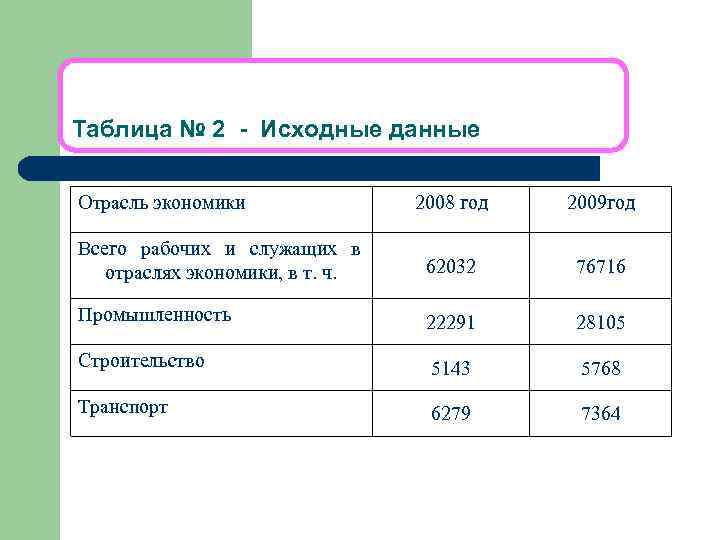Таблица № 2 - Исходные данные Отрасль экономики 2008 год 2009 год Всего рабочих и служащих в отраслях экономики, в т. ч. 62032 76716 Промышленность 22291 28105 Строительство 5143 5768 Транспорт 6279 7364

Решение: Относительная величина структуры: За 2008 год: 5143+6279=11422 (тыс. чел. ) 11422(тыс. чел. ) / 22291(тыс. чел. ) *100 % = 0, 512 * 100 % = 51, 24 % Т. е. отношение численности работников строительства и транспорта к работникам промышленности составляет 51, 24 % это относительная величина структуры, она показывает долю (удельный вес) составных частей целого в их общем итоге. За 2009 год: 5768+7364=13132 (тыс. чел. ) 13132(тыс. чел. ) / 28105(тыс. чел. ) *100 % = 0, 47 * 100 % = 47 % Относительные величины динамики характеризуют развитие изучаемого явления во времени (ОВД). ОВД =Текущий показатель / Предшествующий (базисный) показатель По промышленности ОВД = 28105 / 22291 = 1, 26 По строительству ОВД = 5768 / 5143 = 1, 12 По транспорту ОВД = 7364 / 6279 = 1, 17 В целом по экономике ОВД = 76716 / 62032 = 1, 24

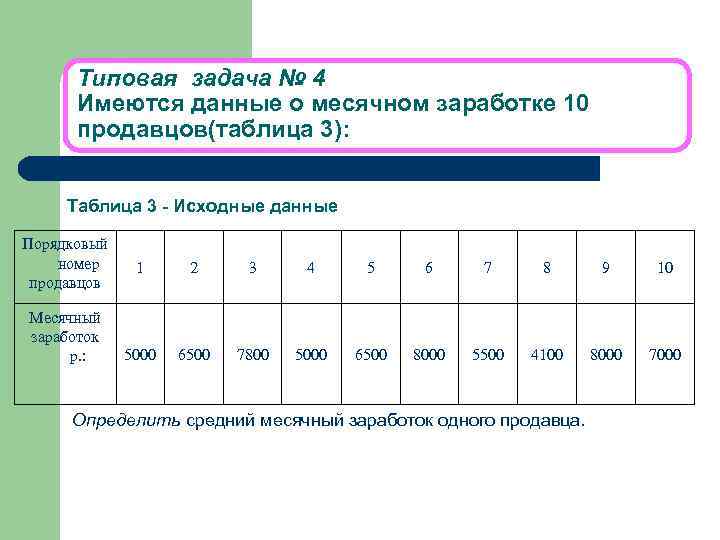Типовая задача № 4 Имеются данные о месячном заработке 10 продавцов(таблица 3): Таблица 3 - Исходные данные Порядковый номер продавцов Месячный заработок р. : 1 2 3 4 5 6 7 8 9 10 5000 6500 7800 5000 6500 8000 5500 4100 8000 7000 Определить средний месячный заработок одного продавца.

Решение: Для определения среднего месячного заработка одного продавца нужно воспользоваться формулой средней арифметической простой, т. к. в задаче даны отдельные значения признака, которая имеет вид: = =(5000+6500+7800+5000+6500+ 8000+5500+4100+8000+7000)/10=6340(р. ) Х Ответ: месячный заработок продавца 6340 р.

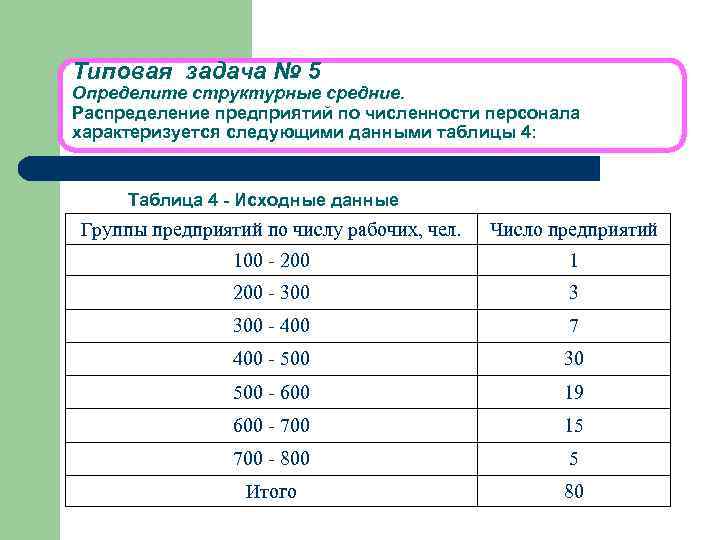Типовая задача № 5 Определите структурные средние. Распределение предприятий по численности персонала характеризуется следующими данными таблицы 4: Таблица 4 - Исходные данные Группы предприятий по числу рабочих, чел. Число предприятий 100 - 200 1 200 - 300 3 300 - 400 7 400 - 500 30 500 - 600 19 600 - 700 15 700 - 800 5 Итого 80

Решение: Определим моду: В таблице 4 наибольшее число предприятий (∑ƒ =30) имеет численность рабочих 400 -500 человек, следовательно, этот интервал является модальным интервалом ряда распределения. Подставим данные из таблицы 6 в формулу: Мо = 400+100*(30 -7)/( (30 -7)+(30 -19))=467, 6=468 (чел. ) Определим медиану: В данной задаче сумма накопленных частот, превышающая половину всех значений (ƒ н =41=11+30), соответствует интервалу 400 -500. Это и есть медианный интервал, в котором находится медиана. Подставим данные в формулу: Ме= 400+100* (0, 5*80 -11) / 30 = 497 (чел. )