Tınaz Ekim Algorithmic graph theory and its applications

Tınaz Ekim Algorithmic graph theory and its applications Tınaz Ekim tinaz. ekim@epfl. ch Swiss Federal Institute of Technology Recherche Opérationnelle Sud Est (ROSE) 23/02/2007 1

Tınaz Ekim Contents PART I (Applications of graph theory) • Introduction to coloring problems • Some examples of applications – – – Biprocessor tasks Frequency assignment Aircraft scheduling University timetabling Sports scheduling 3 D image reconstruction PART II (Generalized coloring problems) • Application : automated storage system • Related results 23/02/2007 2

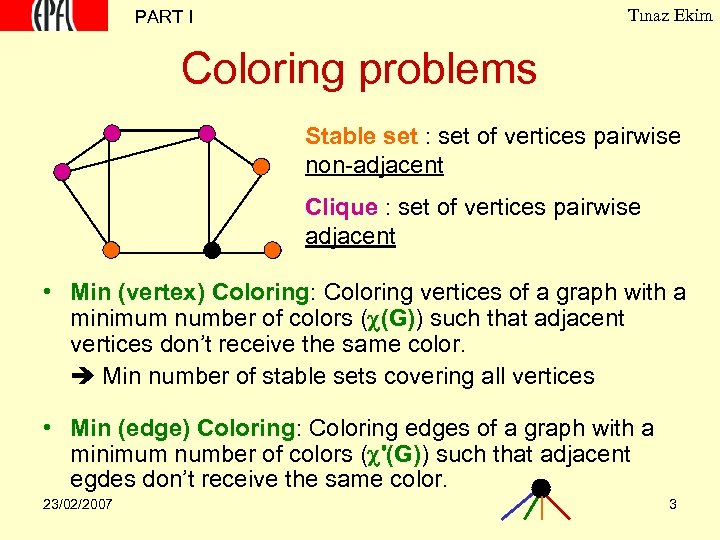Tınaz Ekim PART I Coloring problems Stable set : set of vertices pairwise non-adjacent Clique : set of vertices pairwise adjacent • Min (vertex) Coloring: Coloring vertices of a graph with a minimum number of colors ( (G)) such that adjacent vertices don’t receive the same color. Min number of stable sets covering all vertices • Min (edge) Coloring: Coloring edges of a graph with a minimum number of colors ( '(G)) such that adjacent egdes don’t receive the same color. 23/02/2007 3

Tınaz Ekim PART I Complexity of coloring problems Min (vertex) Coloring NP-hard [Karp, 72] Min (edge) Coloring NP-hard [Holyer, 81] NP-hard : P=NP or P NP ? (1. 000 $ question) 23/02/2007 n 5 2 n 10 0. 1 sc 0. 001 sc 20 3. 2 sc 1 sc 30 24. 3 sc 17. 9 mn 40 No polynomial time exact algorithm is known, and most probably, there is no such an algorithm ! n 1. 7 mn 12. 7 days 50 5. 2 mn 35. 7 years 60 13. 0 mn 366 centuries 4

PART I Tınaz Ekim Methods to cope with NP-hard problems: 1. Restriction to particular cases – – becomes polynomially solvable (give an exact algorithm), or remains NP-hard (give the proof) 2. Approximation with performance guarantee – – approximation ratio quality measure -approximation algo. |A| |OPT| ( 1 if min) 3. Heuristics to obtain relatively «good» solutions in a reasonable time 23/02/2007 5

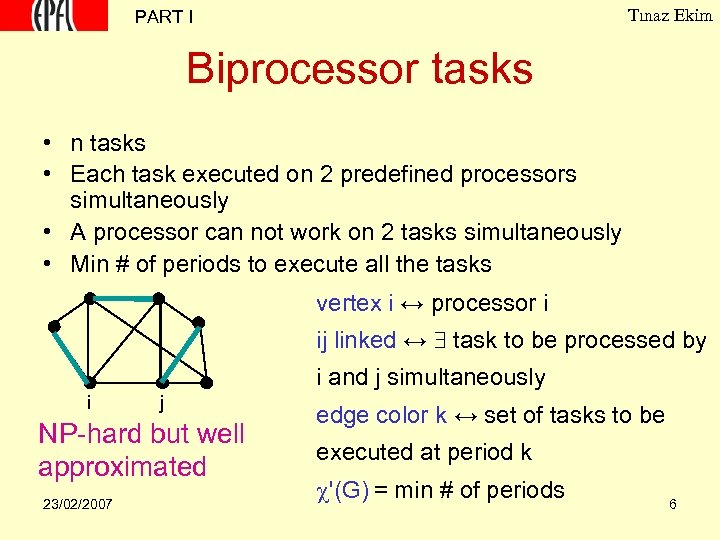Tınaz Ekim PART I Biprocessor tasks • n tasks • Each task executed on 2 predefined processors simultaneously • A processor can not work on 2 tasks simultaneously • Min # of periods to execute all the tasks vertex i ↔ processor i ij linked ↔ task to be processed by i and j simultaneously i j NP-hard but well approximated 23/02/2007 edge color k ↔ set of tasks to be executed at period k '(G) = min # of periods 6

Tınaz Ekim PART I Frequency assignment • n base stations • same frequency for close stations interference • Min of frequencies vertex i ↔ station i ij linked ↔ possible interference between i and j color ↔ set of stations that can have G disk unit graph 3 -approximation 23/02/2007 the same frequency (G) = min # of frequencies 7

Tınaz Ekim PART I Aircraft scheduling • n flights • Time interval of flight i is (ai, bi) • Min number of aircrafts to be assigned vertex i ↔ flight i ij linked ↔ (ai, bi) overlaps (aj, bj) color ↔ set of flights scheduled to the same aircraft i j (G) = min number of aircrafts G interval graph polynomial 23/02/2007 8

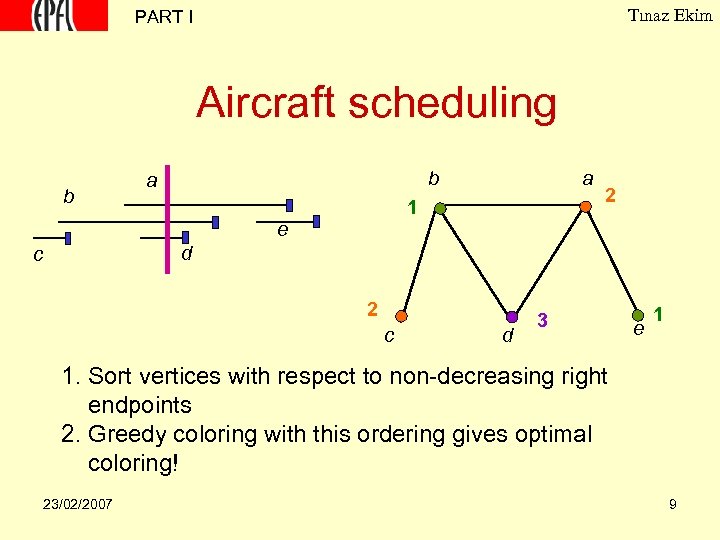Tınaz Ekim PART I Aircraft scheduling b b a a 1 2 e d c 2 c d 3 e 1 1. Sort vertices with respect to non-decreasing right endpoints 2. Greedy coloring with this ordering gives optimal coloring! 23/02/2007 9

PART I Tınaz Ekim Various constraints 1. Cardinality constraint: each color set can have at most t vertices Limited resource (machine) in scheduling problems Aircrafts: each aircraft can fly at most t times / period → becomes NP-hard in interval graphs [de Werra, Kobler, 03] 2. Precoloring extension: some vertices are already assigned to some colors Certain jobs are already assigned Aircrafts: some flights are already assigned to some aircrafts → becomes NP-hard in interval graphs [Biro, Hujter, Tuza, 92] 3. List coloring: restricted set of colors for each vertex Job that can be processed only in certain time periods, or only by certain machines Aircrafts: some flights can only be executed by some aircrafts → at least as difficult as precoloring extension 23/02/2007 10

PART I Tınaz Ekim University timetabling • • • Students choose courses in a list (time slot + prof. ) Probability pi for course i to be opened pi = 1 if i is a mandatory course Objective: min of rooms vertex i ↔ course i ij linked ↔ i and j can not be in the same room color ↔ set of courses assigned to the same room Min expected # of rooms: Min Ck [1 - (i Ck)(1 -pi)] NP-hard even in bipartite graphs [Murat, Paschos, 2006] 23/02/2007 11

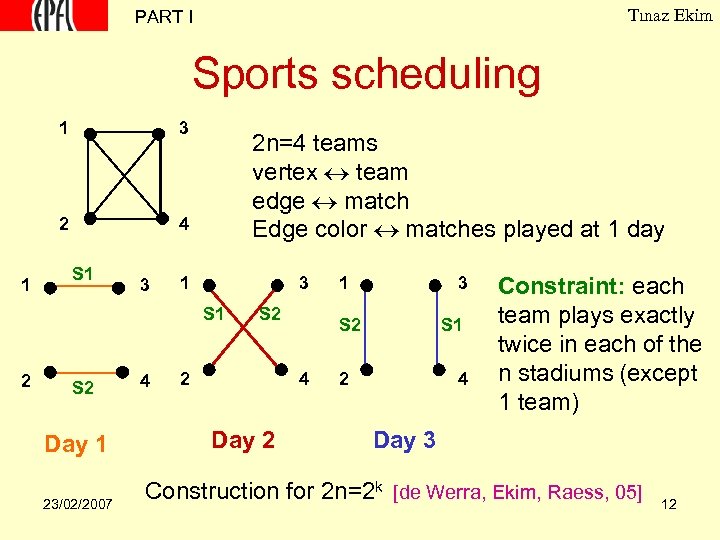Tınaz Ekim PART I Sports scheduling 1 2 1 3 4 S 1 3 2 n=4 teams vertex team edge match Edge color matches played at 1 day 1 3 S 1 2 S 2 Day 1 23/02/2007 4 S 2 2 3 S 2 4 Day 2 1 S 1 2 4 Constraint: each team plays exactly twice in each of the n stadiums (except 1 team) Day 3 Construction for 2 n=2 k [de Werra, Ekim, Raess, 05] 12

PART I Tınaz Ekim 3 D image reconstruction [R. Zenklusen, Master’s thesis, 2005 (OR + Computer Vision)] • Images of the surface 3 D reconstruction problem • Usually reduced to 1 D problem oversimplified • 3 D reconstruction using graph flows [Roy, 1999] 23/02/2007 13

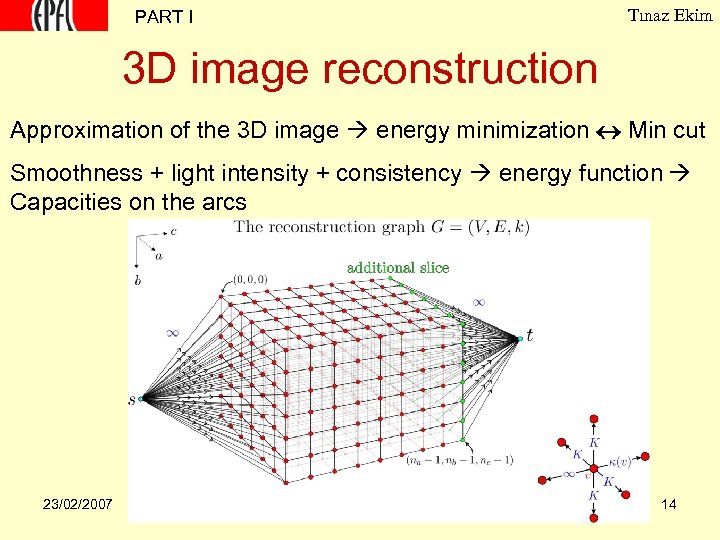PART I Tınaz Ekim 3 D image reconstruction Approximation of the 3 D image energy minimization Min cut Smoothness + light intensity + consistency energy function Capacities on the arcs 23/02/2007 14

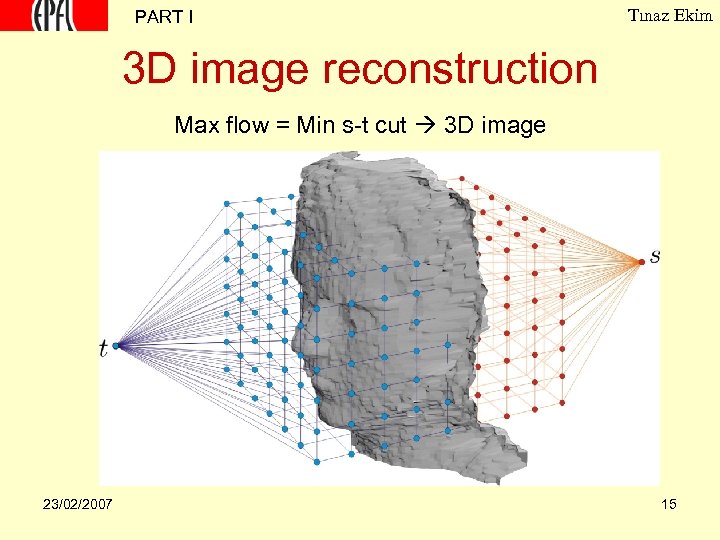PART I Tınaz Ekim 3 D image reconstruction Max flow = Min s-t cut 3 D image 23/02/2007 15

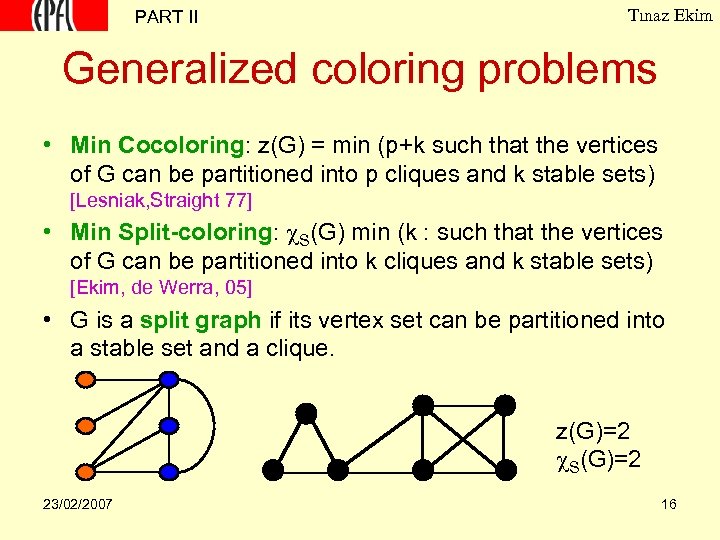PART II Tınaz Ekim Generalized coloring problems • Min Cocoloring: z(G) = min (p+k such that the vertices of G can be partitioned into p cliques and k stable sets) [Lesniak, Straight 77] • Min Split-coloring: S(G) min (k : such that the vertices of G can be partitioned into k cliques and k stable sets) [Ekim, de Werra, 05] • G is a split graph if its vertex set can be partitioned into a stable set and a clique. z(G)=2 S(G)=2 23/02/2007 16

Tınaz Ekim PART II Permutation graphs Given a permutation (N) where N= 1, … , n the permutation graph G=(V, E) corresponding to is defined as follows: V= 1, … , n and ij E iff i < j and (i) > (j) 5 1 3 7 6 2 4 2 7 clique = decreasing subsequence 3 6 4 23/02/2007 5 1 stable set= increasing subsequence 17

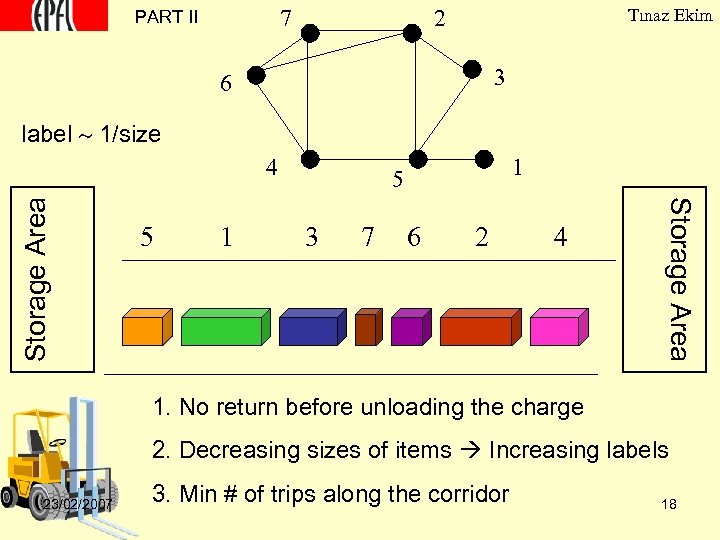7 PART II 2 Tınaz Ekim 3 6 label 1/size 5 1 1 5 3 7 6 2 4 Storage Area 4 1. No return before unloading the charge 2. Decreasing sizes of items Increasing labels 23/02/2007 3. Min # of trips along the corridor 18

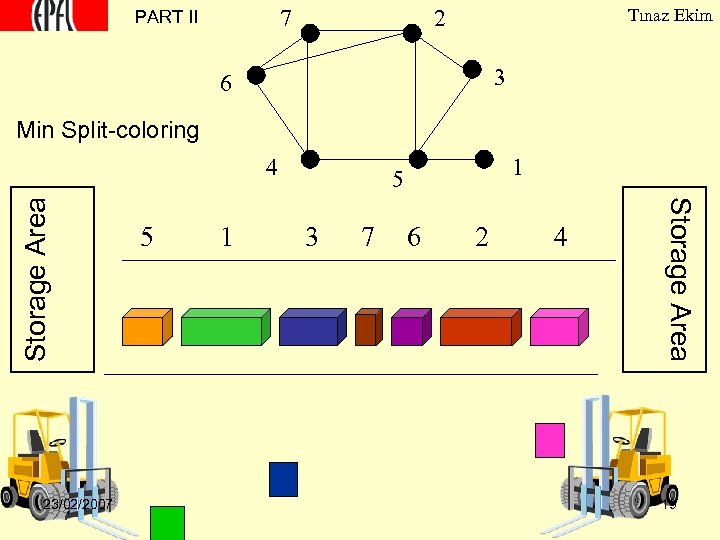7 PART II 2 Tınaz Ekim 3 6 Min Split-coloring 23/02/2007 5 1 1 5 3 7 6 2 4 Storage Area 4 19

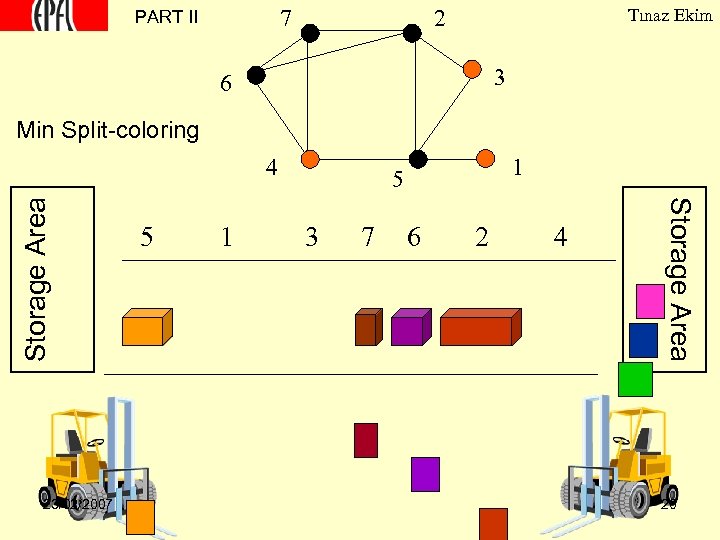7 PART II 2 Tınaz Ekim 3 6 Min Split-coloring 23/02/2007 5 1 1 5 3 7 6 2 4 Storage Area 4 20

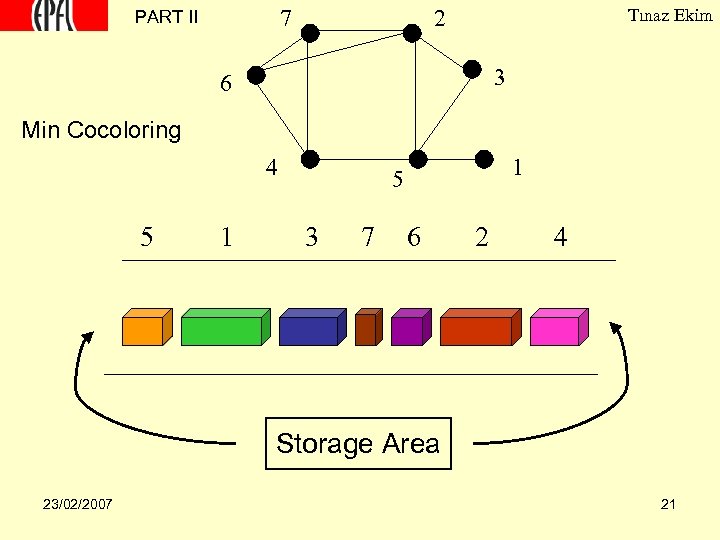7 PART II 2 Tınaz Ekim 3 6 Min Cocoloring 4 5 1 1 5 3 7 6 2 4 Storage Area 23/02/2007 21

PART II Tınaz Ekim Complexity results • Min Split-coloring and Min Cocoloring NP-hard, differential approximation scheme ((1 - )-approximation, for all >0) [Demange, Ekim, de Werra, 06] • Min Cocoloring NP-hard in permutation gr. [Wagner, 84] • Min Split-coloring NP-hard in permutation graphs but 2 approximable [Demange, Ekim, de Werra, 06] • Min l-modal NP-hard, differential approximation scheme • Min Split-coloring and Min Cocoloring P in cacti [Ekim, de Werra, 05], cographs [Demange, Ekim, de Werra, 05], in chordal graphs [Hell et al. 04]. • Min Cocoloring P in L(Bipartite), L(line-perfect graph), Min Split-coloring NP-hard in L(Bipartite) [Demange, Ekim, de Werra, 05] 23/02/2007 22

Tınaz Ekim Conclusions • Several open questions related to permutations • On-line models for robotics problems • Telecommunication (network design, network security), production systems (scheduling, stock management), transportation (distribution, routing), computer vision, robotics, etc. Combinatorial optimization problems • New challenges for both theoretical and algorithmic aspects 23/02/2007 23

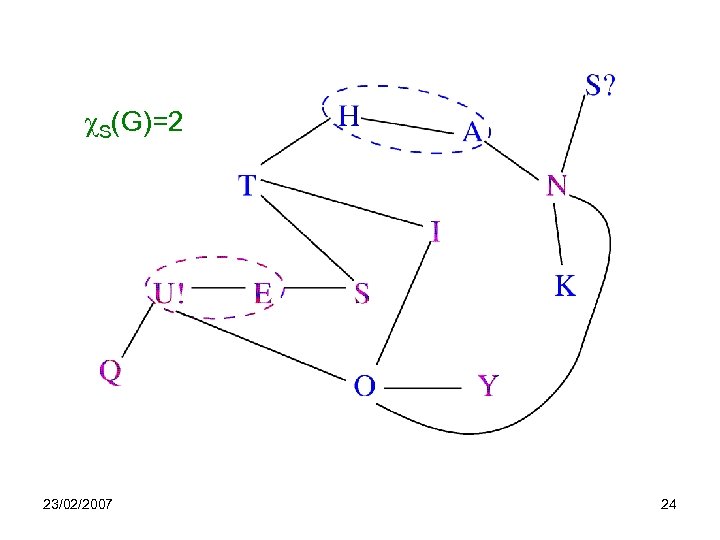S(G)=2 23/02/2007 24