Timing Optimization in Logic with Interconnect Arkadiy Morgenshtein

Timing Optimization in Logic with Interconnect Arkadiy Morgenshtein, Eby G. Friedman, Ran Ginosar, Avinoam Kolodny Technion – Israel Institute of Technology SLIP (System Level Interconnect Prediction) 2008 1

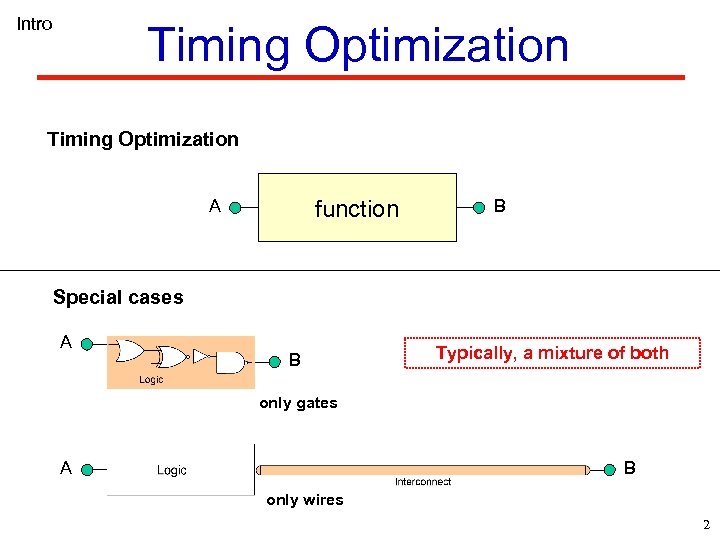Intro Timing Optimization function A B Special cases A B Typically, a mixture of both only gates B A only wires 2

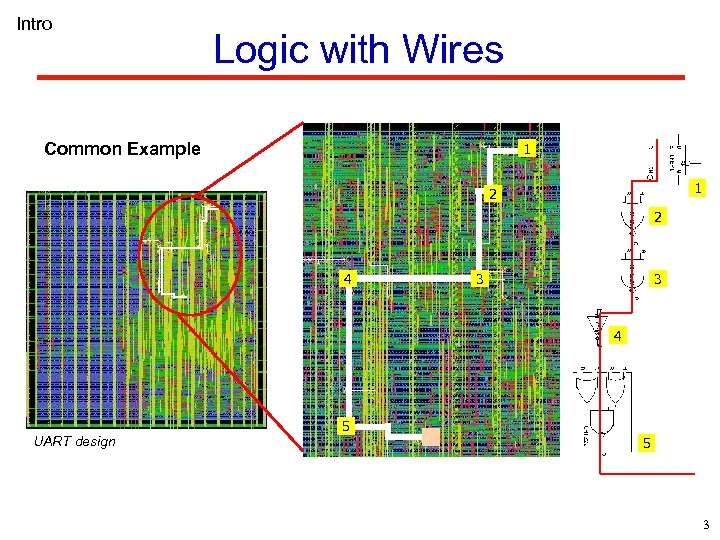Intro Logic with Wires Common Example 1 1 2 2 4 3 3 4 UART design 5 5 3

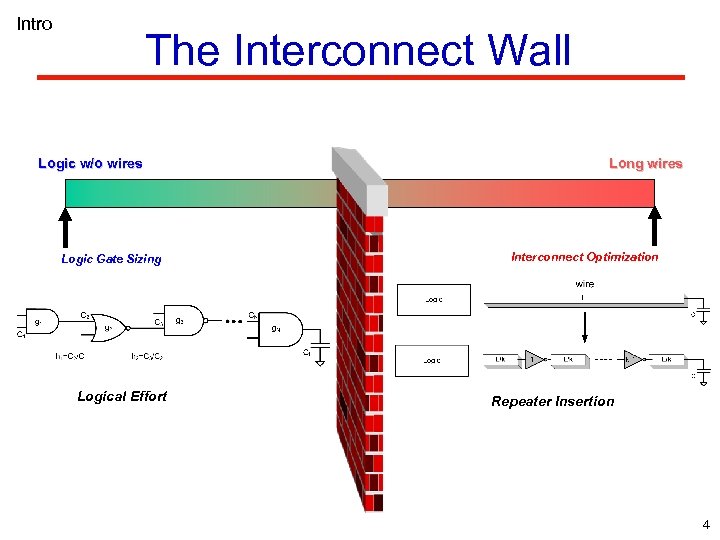Intro The Interconnect Wall Logic w/o wires Logic Gate Sizing Logical Effort Long wires Interconnect Optimization Repeater Insertion 4

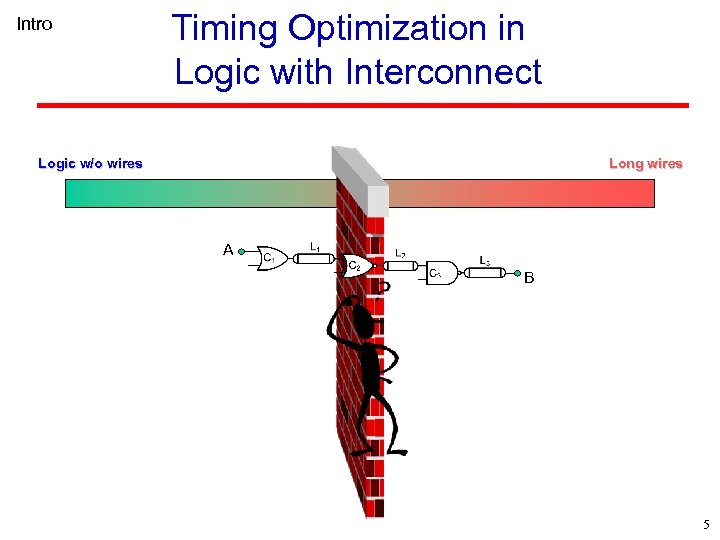Intro Timing Optimization in Logic with Interconnect Logic w/o wires Long wires A B 5

Existing Techniques A (very) Short Tutorial 6

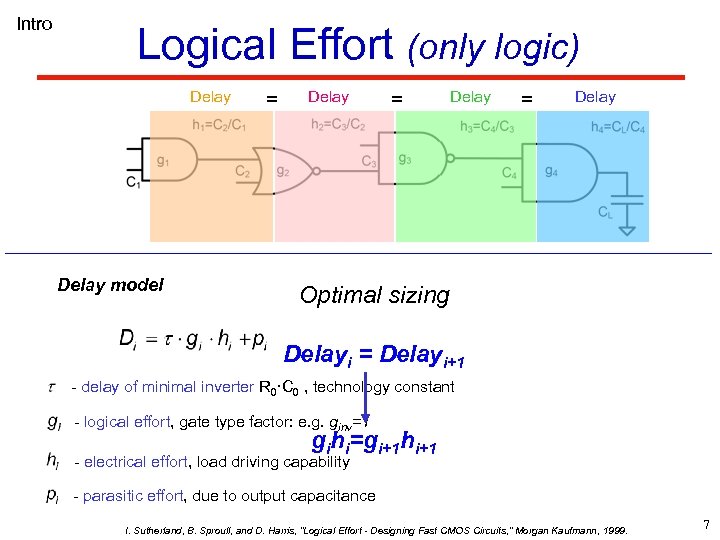Intro Logical Effort (only logic) Delay model = Delay Optimal sizing Delayi = Delayi+1 - delay of minimal inverter R 0·C 0 , technology constant - logical effort, gate type factor: e. g. ginv=1 gihi=gi+1 hi+1 - electrical effort, load driving capability - parasitic effort, due to output capacitance I. Sutherland, B. Sproull, and D. Harris, “Logical Effort - Designing Fast CMOS Circuits, ” Morgan Kaufmann, 1999. 7

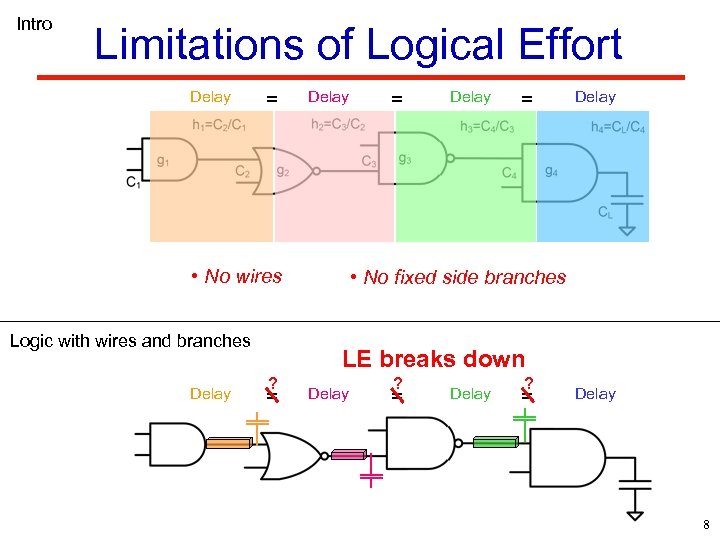Intro Limitations of Logical Effort Delay = Delay • No wires Logic with wires and branches Delay = Delay • No fixed side branches LE breaks down ? = Delay 8

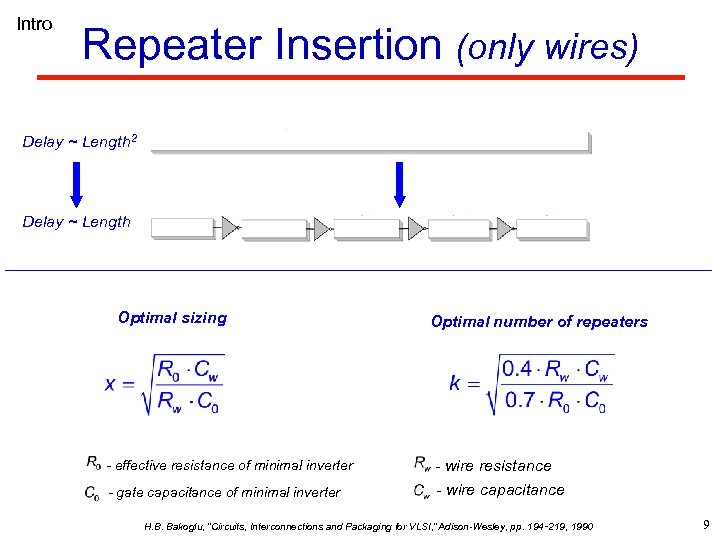Intro Repeater Insertion (only wires) Delay ~ Length 2 D = RC = 25 Delay ~ Length D = Σrc = 5 Optimal sizing Optimal number of repeaters - effective resistance of minimal inverter - wire resistance - gate capacitance of minimal inverter - wire capacitance H. B. Bakoglu, “Circuits, Interconnections and Packaging for VLSI, ” Adison-Wesley, pp. 194‑ 219, 1990 9

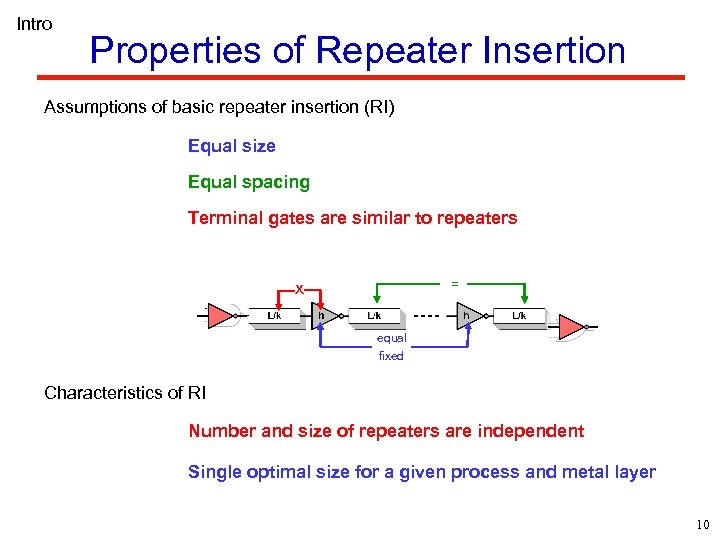Intro Properties of Repeater Insertion Assumptions of basic repeater insertion (RI) Equal size Equal spacing Terminal gates are similar to repeaters = x equal fixed Characteristics of RI Number and size of repeaters are independent Single optimal size for a given process and metal layer 10

So, What Are We Going To Do? 11

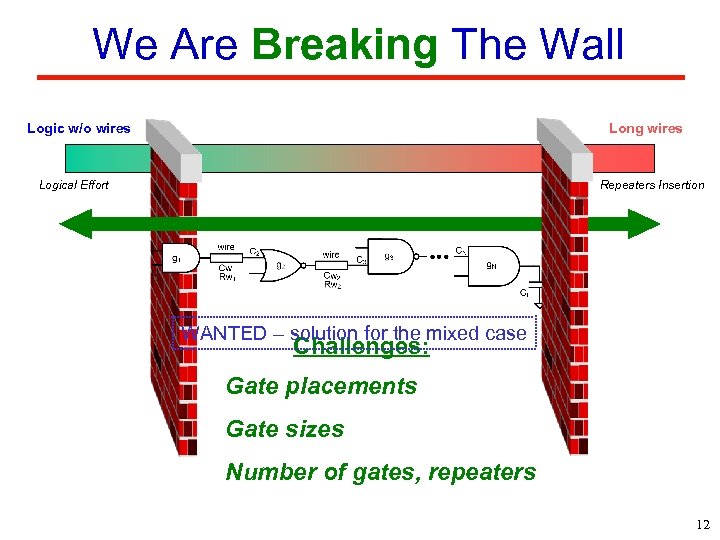Intro We Are Breaking The Wall Logic w/o wires Long wires Logical Effort Repeaters Insertion WANTED – solution for the mixed case Challenges: Gate placements Gate sizes Number of gates, repeaters 12

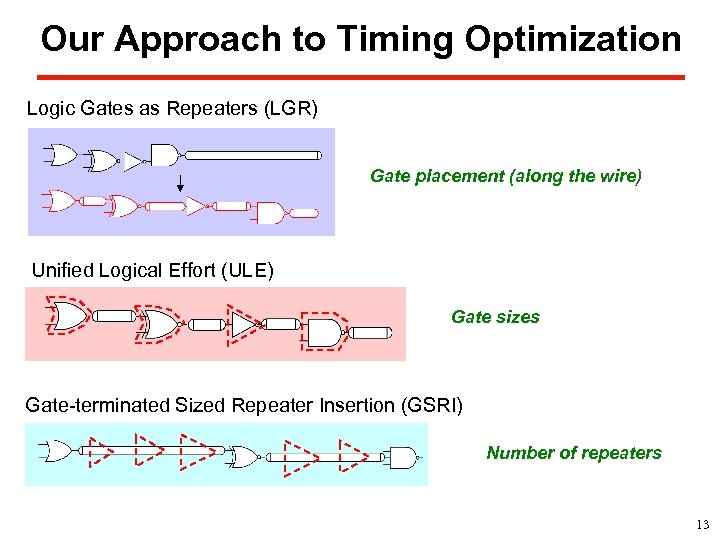Our Approach to Timing Optimization Logic Gates as Repeaters (LGR) Gate placement (along the wire) Unified Logical Effort (ULE) Gate sizes Gate-terminated Sized Repeater Insertion (GSRI) Number of repeaters 13

Logic Gates as Repeaters - LGR “Where should the gates be located (along the wire)? ” 14

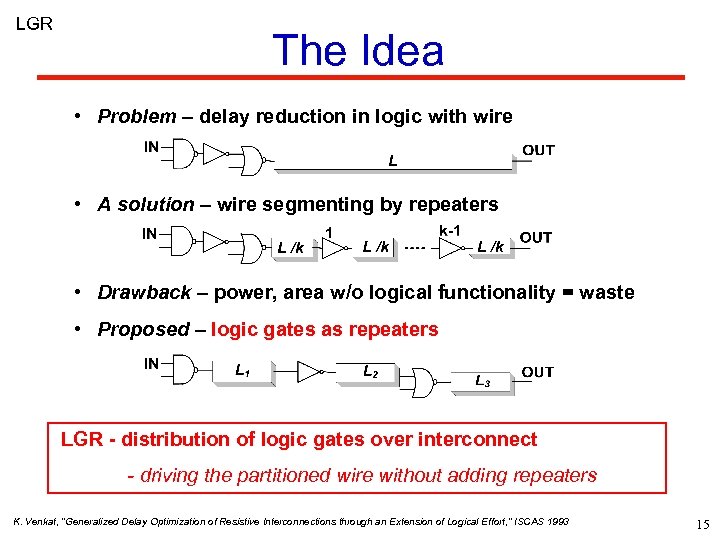LGR The Idea • Problem – delay reduction in logic with wire • A solution – wire segmenting by repeaters • Drawback – power, area w/o logical functionality = waste • Proposed – logic gates as repeaters LGR - distribution of logic gates over interconnect - driving the partitioned wire without adding repeaters K. Venkat, “Generalized Delay Optimization of Resistive Interconnections through an Extension of Logical Effort, ” ISCAS 1993 15

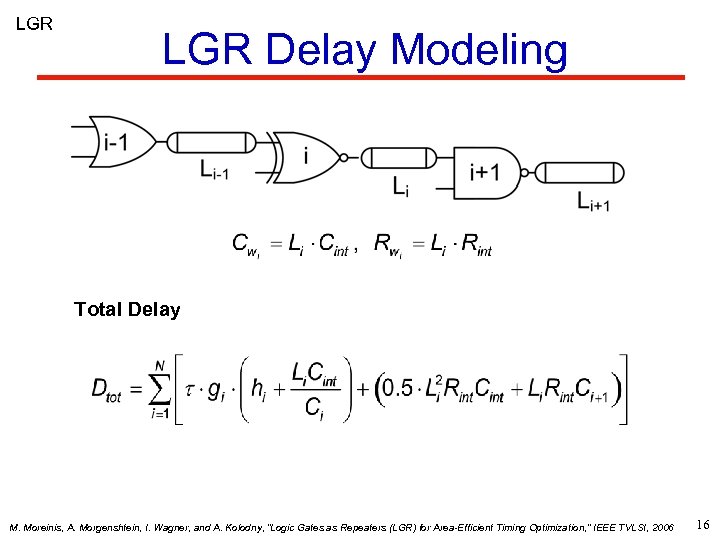LGR Delay Modeling Total Delay M. Moreinis, A. Morgenshtein, I. Wagner, and A. Kolodny, “Logic Gates as Repeaters (LGR) for Area-Efficient Timing Optimization, ” IEEE TVLSI, 2006 16

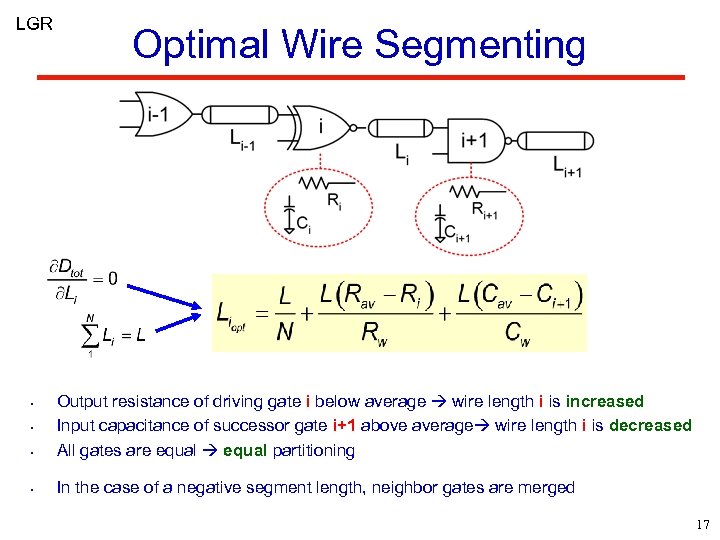LGR Optimal Wire Segmenting • Output resistance of driving gate i below average wire length i is increased Input capacitance of successor gate i+1 above average wire length i is decreased All gates are equal partitioning • In the case of a negative segment length, neighbor gates are merged • • 17

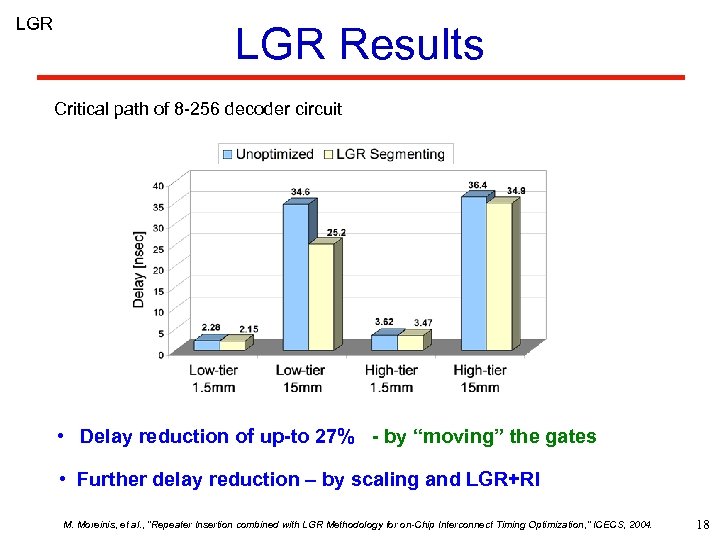LGR Results Critical path of 8 -256 decoder circuit • Delay reduction of up-to 27% - by “moving” the gates • Further delay reduction – by scaling and LGR+RI M. Moreinis, et al. , “Repeater Insertion combined with LGR Methodology for on-Chip Interconnect Timing Optimization, ” ICECS, 2004. 18

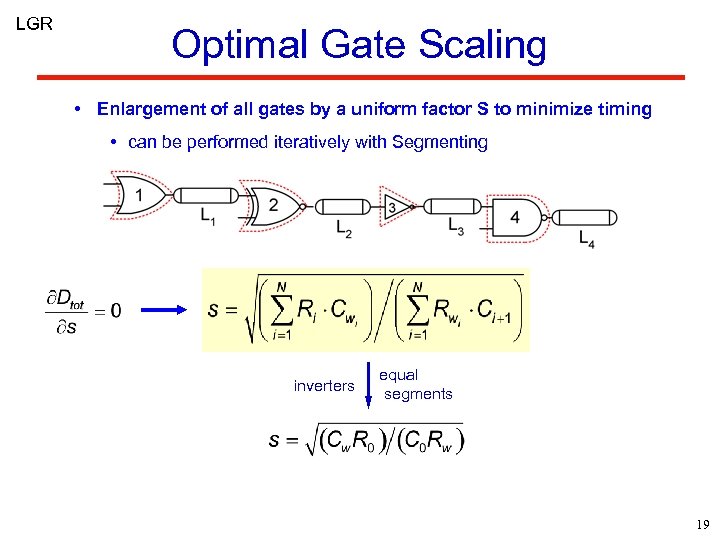LGR Optimal Gate Scaling • Enlargement of all gates by a uniform factor S to minimize timing • can be performed iteratively with Segmenting inverters equal segments 19

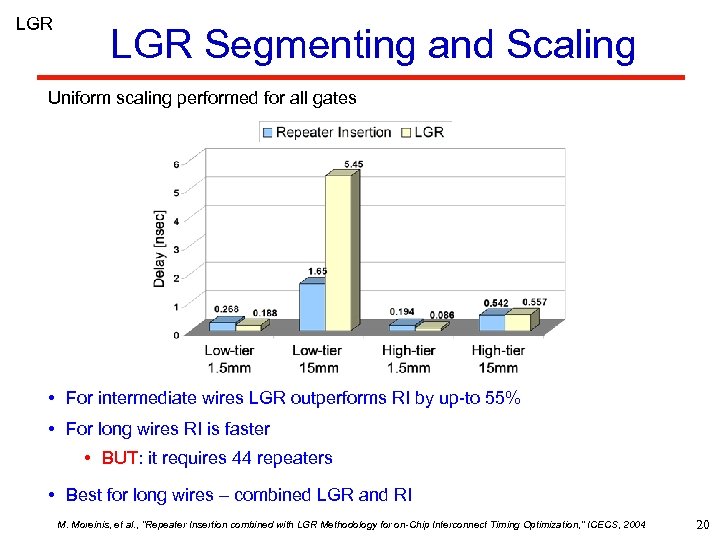LGR Segmenting and Scaling Uniform scaling performed for all gates • For intermediate wires LGR outperforms RI by up-to 55% • For long wires RI is faster • BUT: it requires 44 repeaters • Best for long wires – combined LGR and RI M. Moreinis, et al. , “Repeater Insertion combined with LGR Methodology for on-Chip Interconnect Timing Optimization, ” ICECS, 2004. 20

LGR Summary • Logic gates serve as repeaters § No need for logically redundant repeaters • Delay reduction + lower area/power • Can be combined with RI 21

Unified Logical Effort - ULE “What is the optimal size of the gates? ” 22

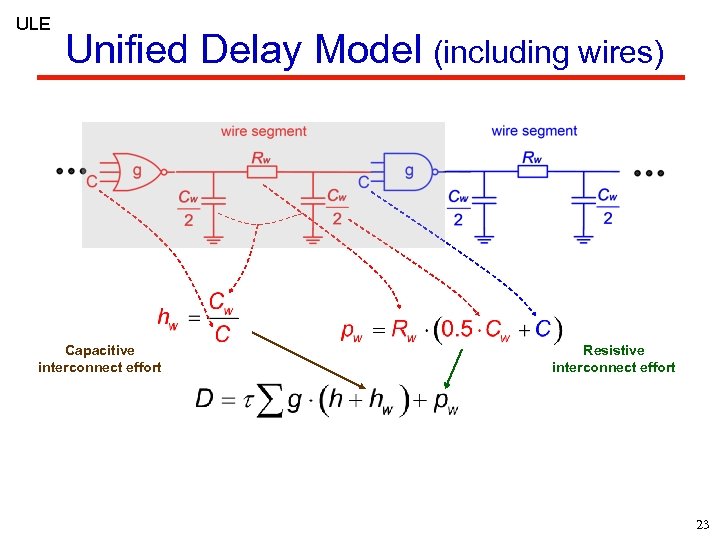ULE Unified Delay Model (including wires) Capacitive interconnect effort Resistive interconnect effort 23

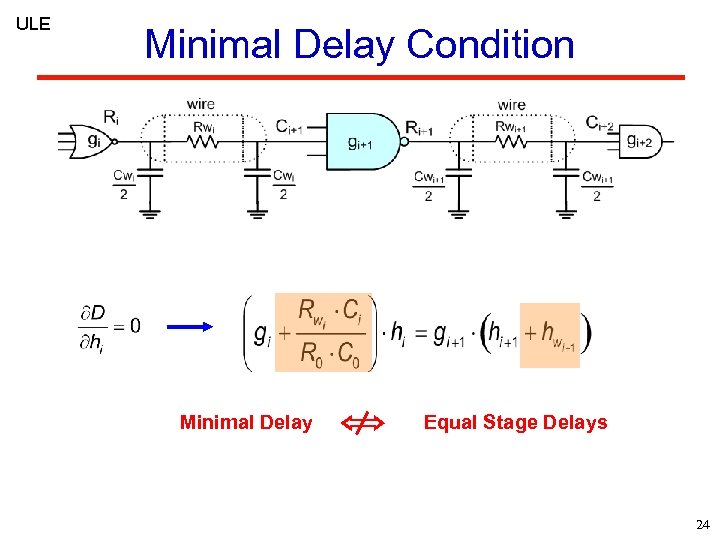ULE Minimal Delay Condition Minimal Delay Equal Stage Delays 24

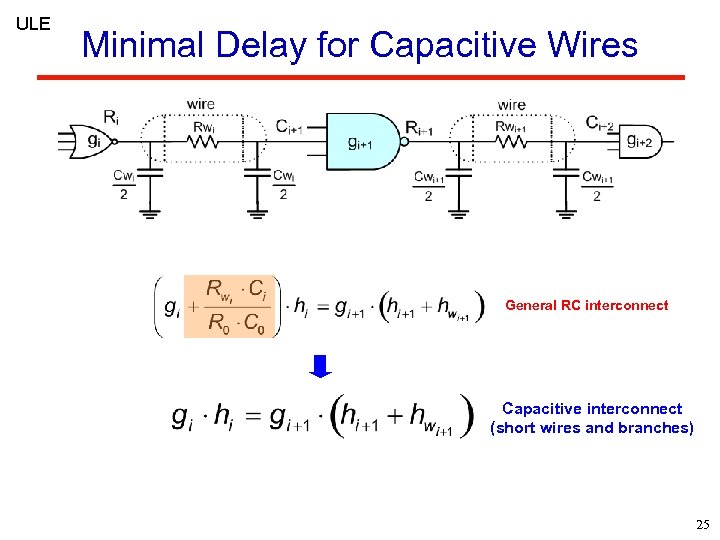ULE Minimal Delay for Capacitive Wires General RC interconnect Capacitive interconnect (short wires and branches) 25

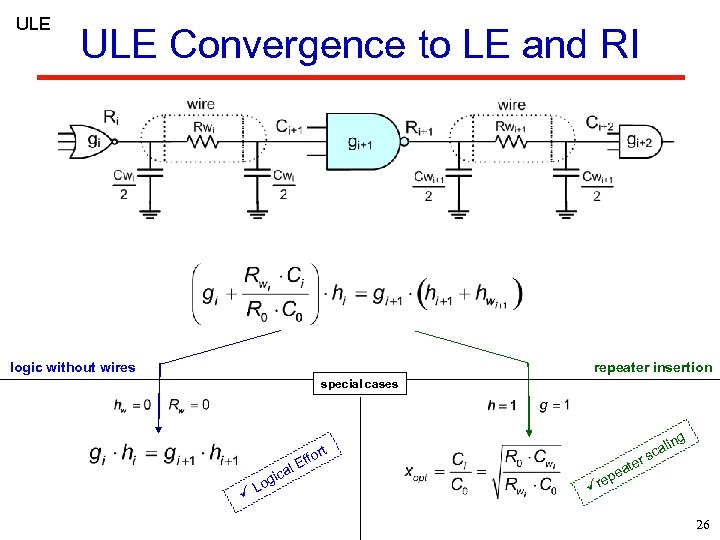ULE Convergence to LE and RI logic without wires repeater insertion special cases ort ff ü L l. E ica og ter ü ea rep g alin sc 26

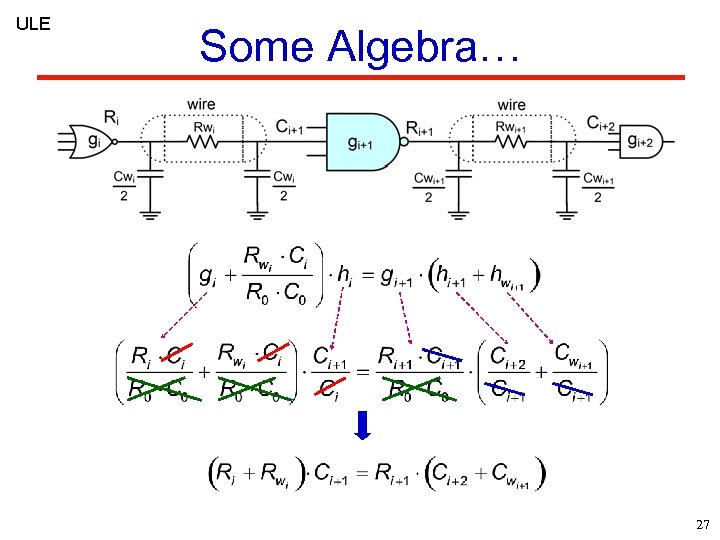ULE Some Algebra… 27

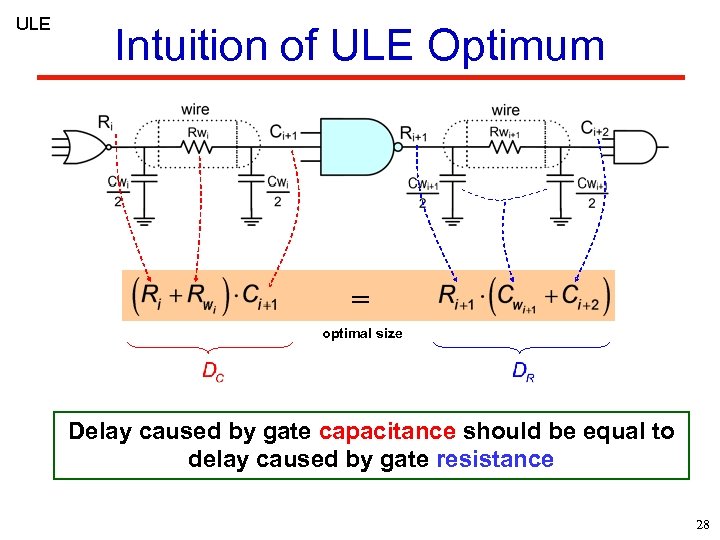ULE Intuition of ULE Optimum = optimal size Delay caused by gate capacitance should be equal to delay caused by gate resistance 28

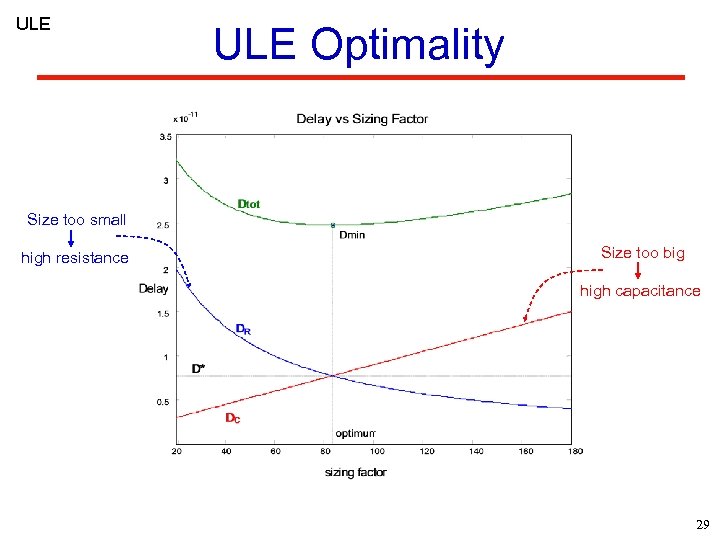ULE Optimality Size too small high resistance Size too big high capacitance 29

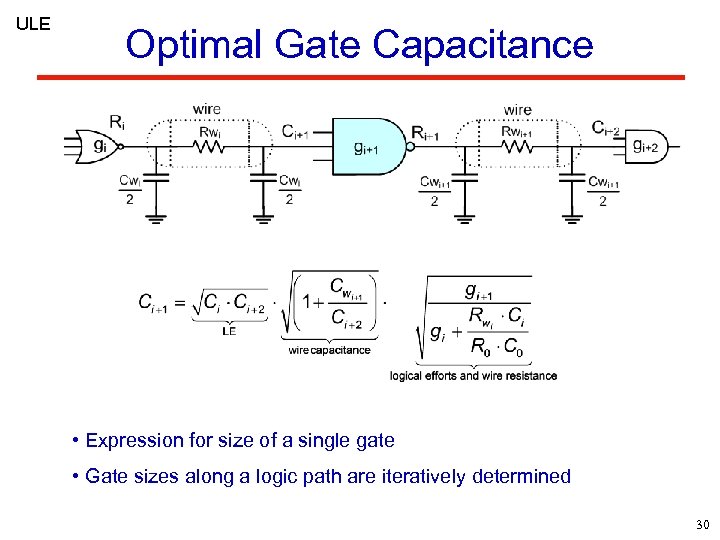ULE Optimal Gate Capacitance • Expression for size of a single gate • Gate sizes along a logic path are iteratively determined 30

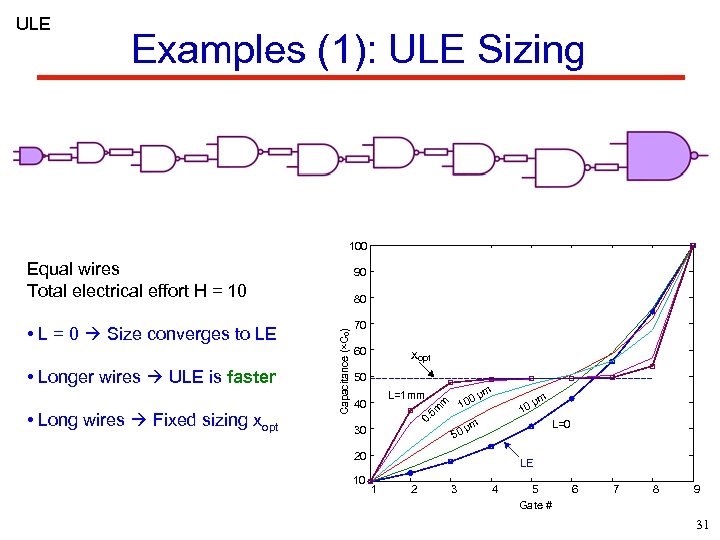ULE Examples (1): ULE Sizing 100 Equal wires Total electrical effort H = 10 • Long wires Fixed sizing xopt 70 60 xopt 50 L=1 mm 40 0 10 0. 5 m m • Longer wires ULE is faster 80 Capacitance (×C 0) • L = 0 Size converges to LE 90 30 50 µm μm L=0 µm 20 10 10 LE 1 2 3 4 5 Gate # 6 7 8 9 31

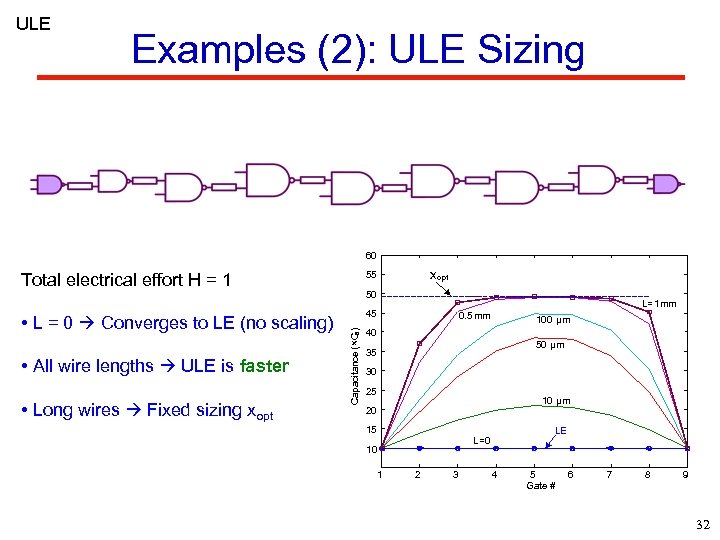ULE Examples (2): ULE Sizing 60 Total electrical effort H = 1 • L = 0 Converges to LE (no scaling) xopt 55 45 • Long wires Fixed sizing xopt Capacitance (×C 0 ) • All wire lengths ULE is faster 50 L=1 mm 0. 5 mm 100 µm 40 50 µm 35 30 25 10 µm 20 15 10 1 LE L=0 2 3 4 5 Gate # 6 7 8 9 32

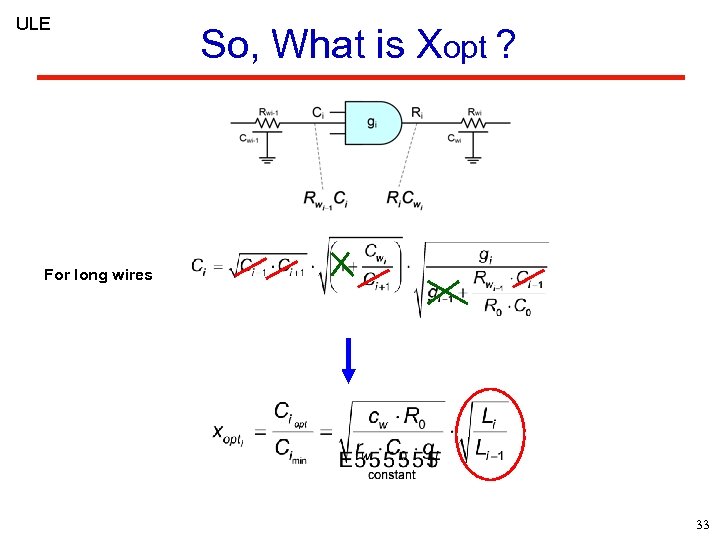ULE So, What is Xopt ? For long wires 33

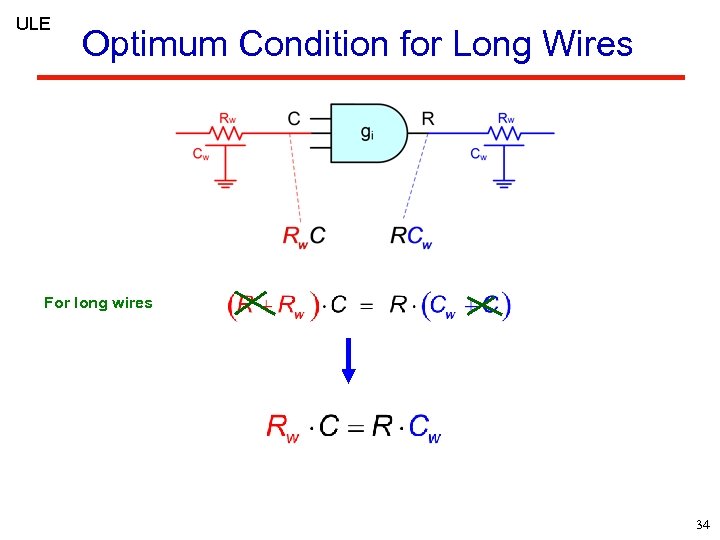ULE Optimum Condition for Long Wires For long wires 34

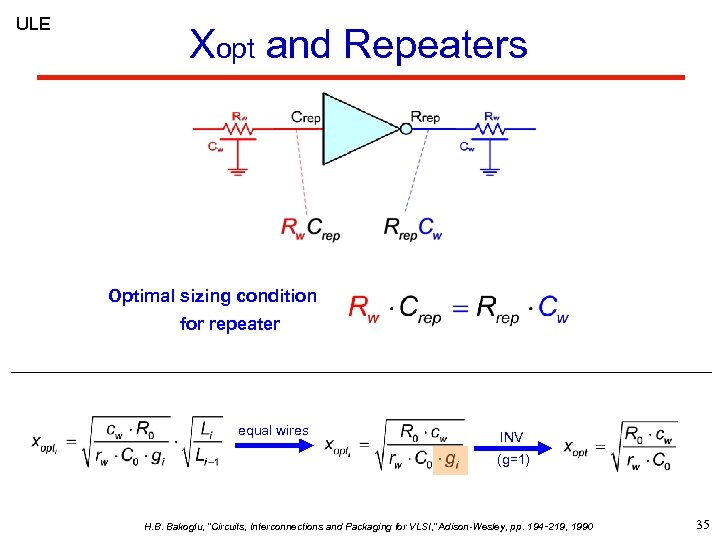ULE Xopt and Repeaters Optimal sizing condition for repeater equal wires INV (g=1) H. B. Bakoglu, “Circuits, Interconnections and Packaging for VLSI, ” Adison-Wesley, pp. 194‑ 219, 1990 35

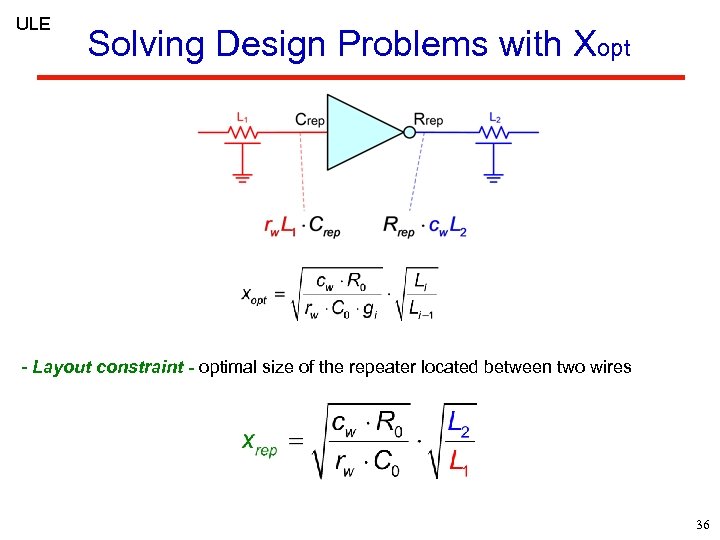ULE Solving Design Problems with Xopt - Layout constraint - optimal size of the repeater located between two wires 36

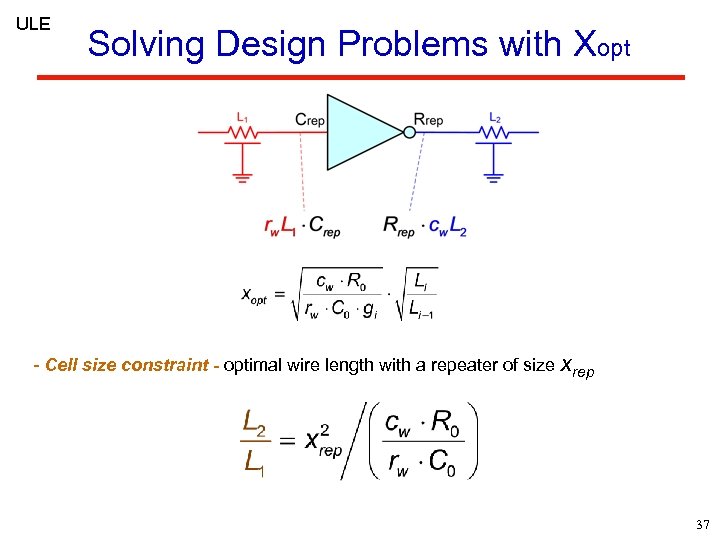ULE Solving Design Problems with Xopt - Cell size constraint - optimal wire length with a repeater of size xrep 37

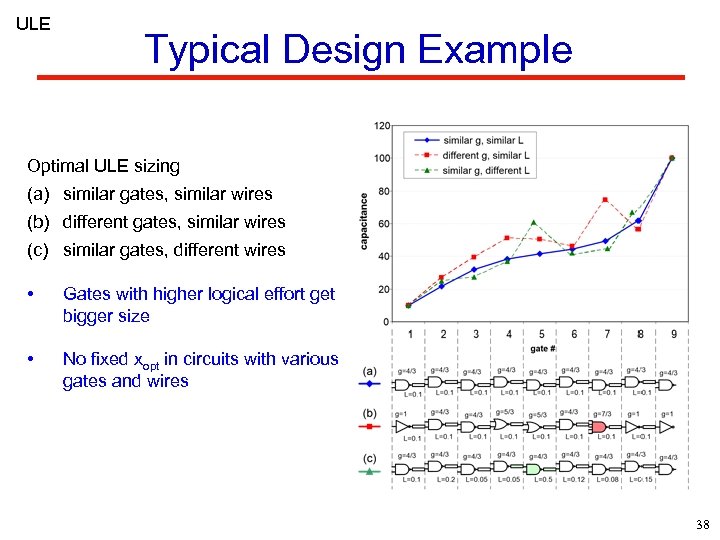ULE Typical Design Example Optimal ULE sizing (a) similar gates, similar wires (b) different gates, similar wires (c) similar gates, different wires • Gates with higher logical effort get bigger size • No fixed xopt in circuits with various gates and wires 38

ULE Results Simulation Setup Critical path in a logic circuit (e. g. Adder) • Compared to Cadence Virtuoso® Analog Optimizer (using numerical algorithms) • 65 nm CMOS 39

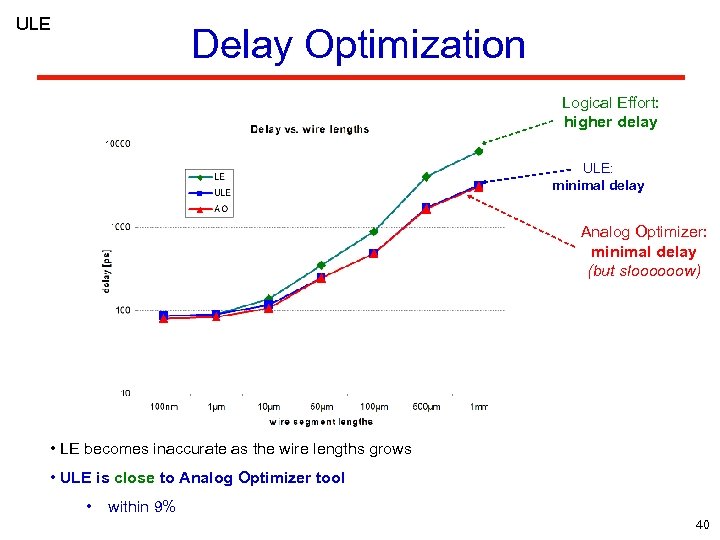ULE Delay Optimization Logical Effort: higher delay ULE: minimal delay Analog Optimizer: minimal delay (but sloooooow) • LE becomes inaccurate as the wire lengths grows • ULE is close to Analog Optimizer tool • within 9% 40

ULE Run time [min] Run Time Comparison • ULE run time is orders of magnitude shorter than the run time of Analog Optimizer • ULE run time is shorter than 1 second 41

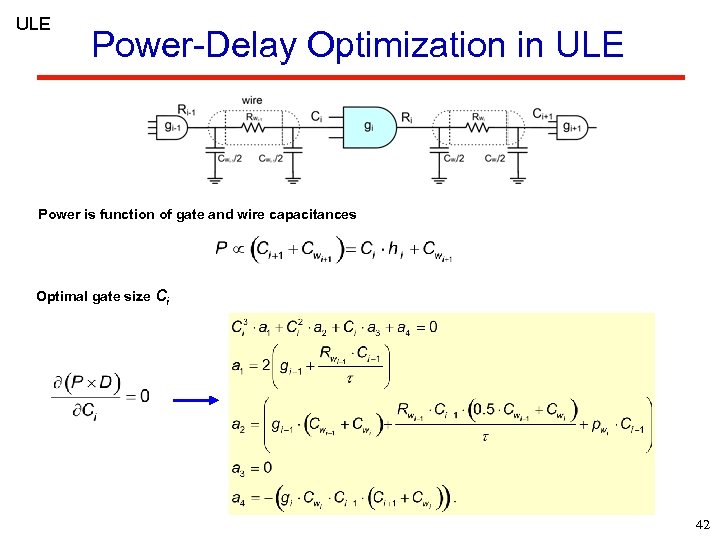ULE Power-Delay Optimization in ULE Power is function of gate and wire capacitances Optimal gate size Ci 42

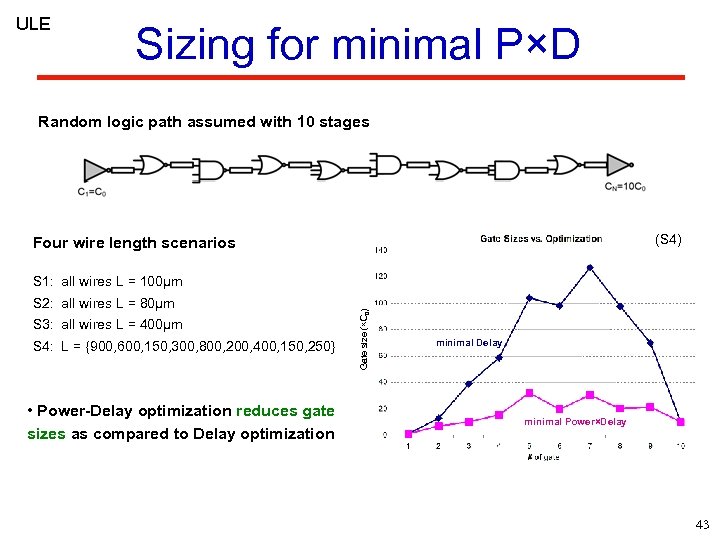ULE Sizing for minimal P×D Random logic path assumed with 10 stages x 1 x 3 x 2 L 1 L 2 x 4 L 3 x 6 X 5 L 4 L 6 L 5 x 8 x 7 L 7 x 9 L 8 X 10 L 9 (S 4) Four wire length scenarios S 2: all wires L = 80µm S 3: all wires L = 400µm S 4: L = {900, 600, 150, 300, 800, 200, 400, 150, 250} • Power-Delay optimization reduces gate sizes as compared to Delay optimization Gate size (×C 0) S 1: all wires L = 100µm minimal Delay minimal Power×Delay 43

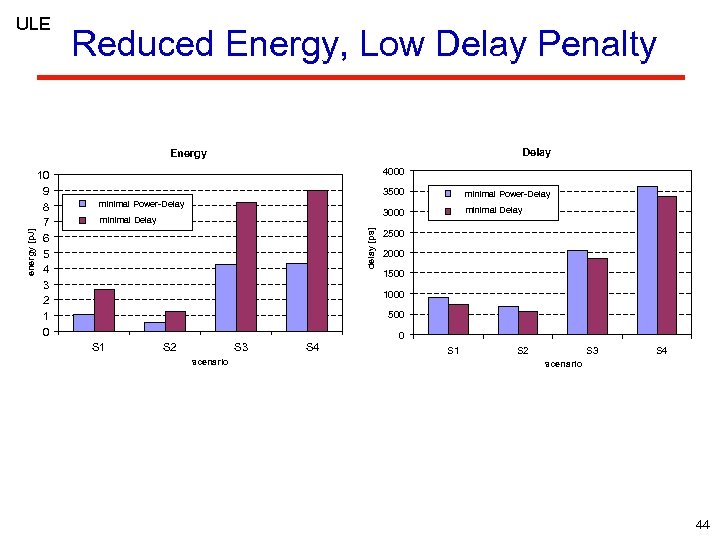ULE Reduced Energy, Low Delay Penalty Delay 10 9 8 7 6 5 4 3 2 1 0 4000 3500 minimal Delay minimal Power-Delay 3000 minimal Power-Delay delay [ps delay (ps) ] energy (p. J)[p. J] energy Energy minimal Delay 2500 2000 1500 1000 500 0 S 1 S 2 S 3 scenario S 4 S 1 S 2 S 3 S 4 scenario 44

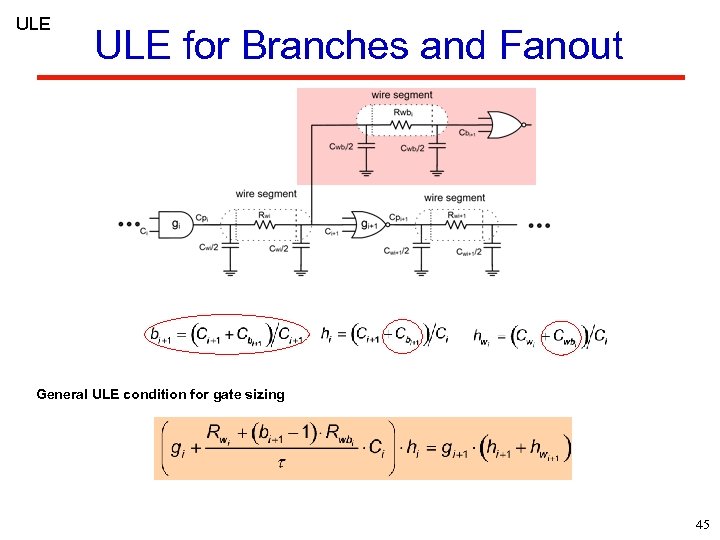ULE for Branches and Fanout General ULE condition for gate sizing 45

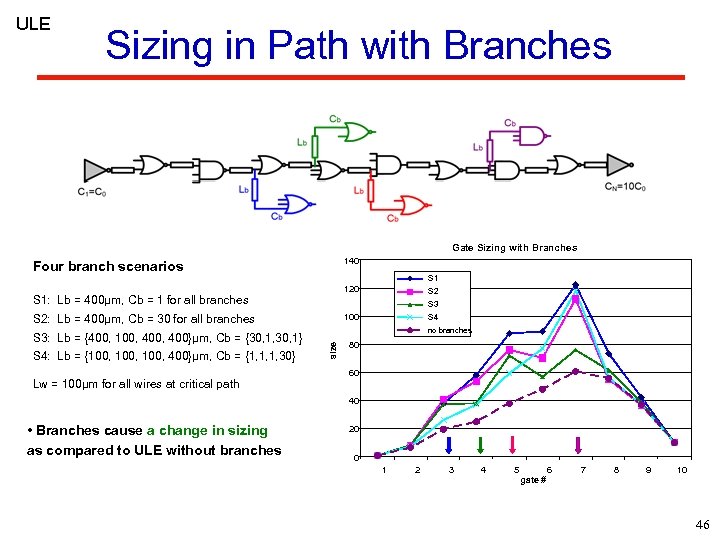ULE Sizing in Path with Branches Gate Sizing with Branches 140 Four branch scenarios S 1 120 S 1: Lb = 400µm, Cb = 1 for all branches S 3 100 S 2: Lb = 400µm, Cb = 30 for all branches S 4: Lb = {100, 400}µm, Cb = {1, 1, 1, 30} Lw = 100µm for all wires at critical path S 4 no branches size S 3: Lb = {400, 100, 400}µm, Cb = {30, 1, 30, 1} S 2 80 60 40 • Branches cause a change in sizing as compared to ULE without branches 20 0 1 2 3 4 5 gate # 6 7 8 9 10 46

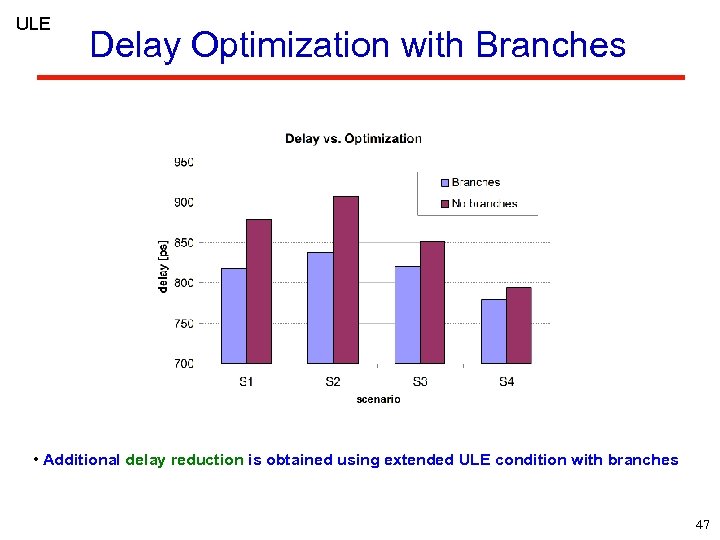ULE Delay Optimization with Branches • Additional delay reduction is obtained using extended ULE condition with branches 47

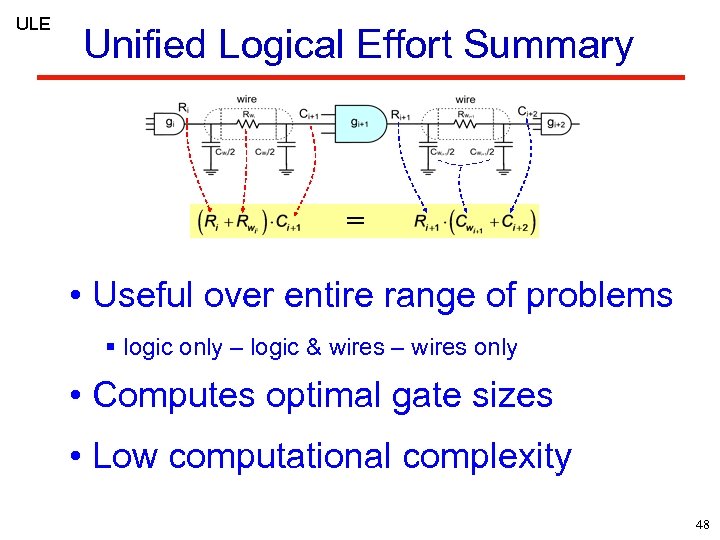ULE Unified Logical Effort Summary = • Useful over entire range of problems § logic only – logic & wires – wires only • Computes optimal gate sizes • Low computational complexity 48

ULE One More Question: “When can I reduce delay by adding an inverter? ” 49

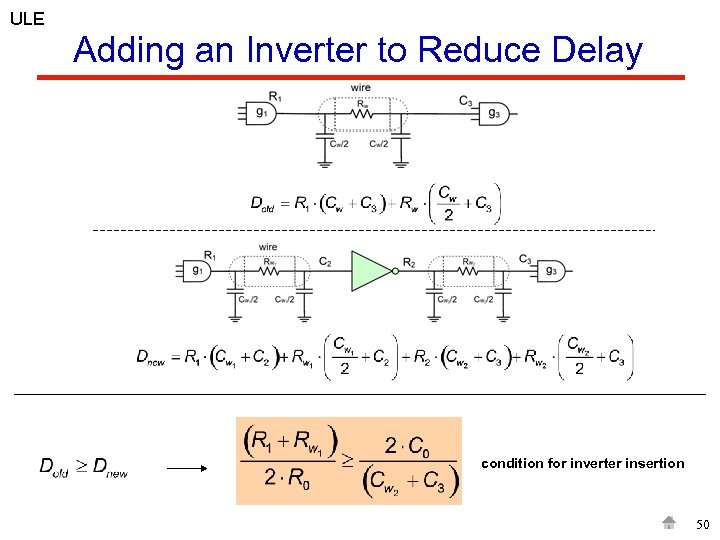ULE Adding an Inverter to Reduce Delay condition for inverter insertion 50

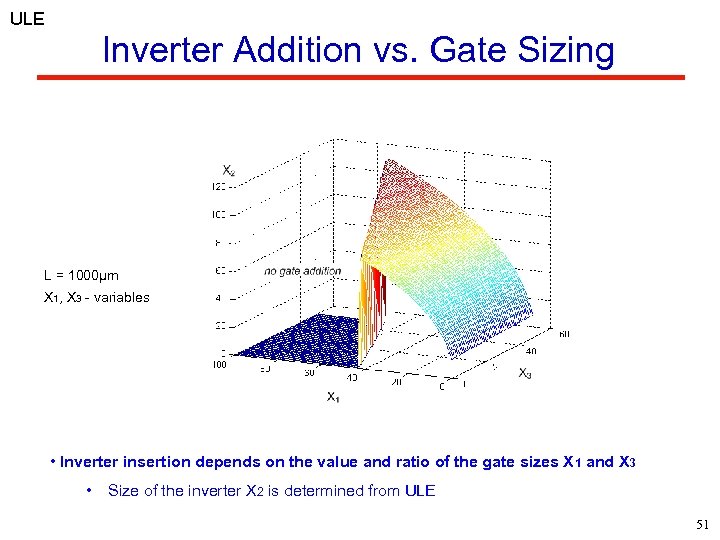ULE Inverter Addition vs. Gate Sizing L = 1000µm X 1, X 3 - variables • Inverter insertion depends on the value and ratio of the gate sizes X 1 and X 3 • Size of the inverter X 2 is determined from ULE 51

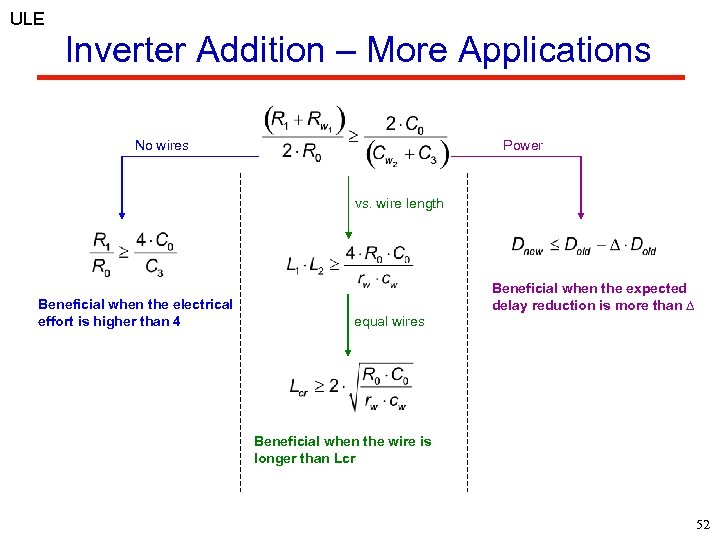ULE Inverter Addition – More Applications No wires Power vs. wire length Beneficial when the electrical effort is higher than 4 Beneficial when the expected delay reduction is more than ∆ equal wires Beneficial when the wire is longer than Lcr 52

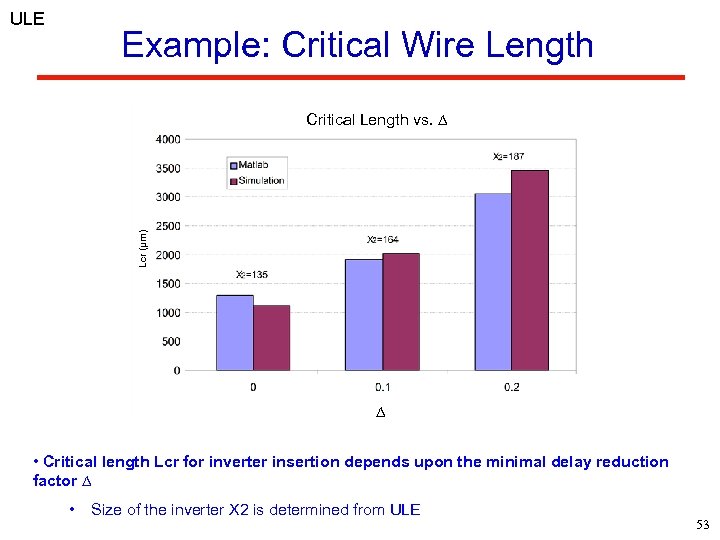ULE Example: Critical Wire Length Lcr (µm) Critical Length vs. ∆ ∆ • Critical length Lcr for inverter insertion depends upon the minimal delay reduction factor ∆ • Size of the inverter X 2 is determined from ULE 53

Gate-Terminated Sized Repeater Insertion - GSRI “What is the optimal number of gates/repeaters? ” 54

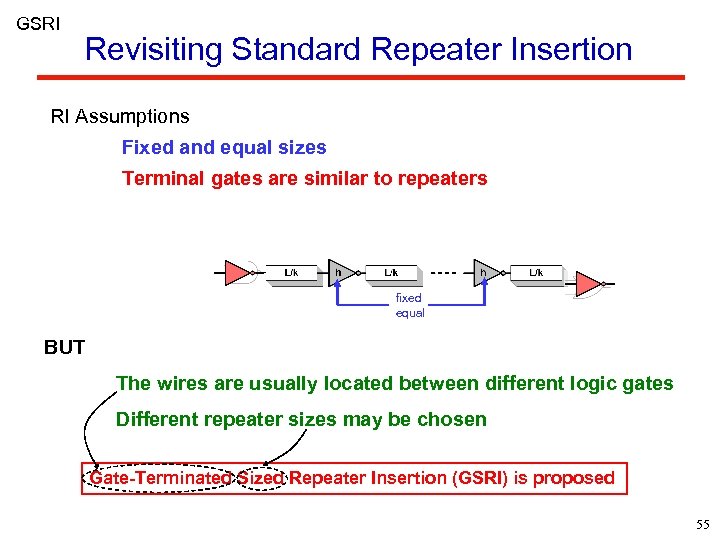GSRI Revisiting Standard Repeater Insertion RI Assumptions Fixed and equal sizes Terminal gates are similar to repeaters fixed equal BUT The wires are usually located between different logic gates Different repeater sizes may be chosen Gate-Terminated Sized Repeater Insertion (GSRI) is proposed 55

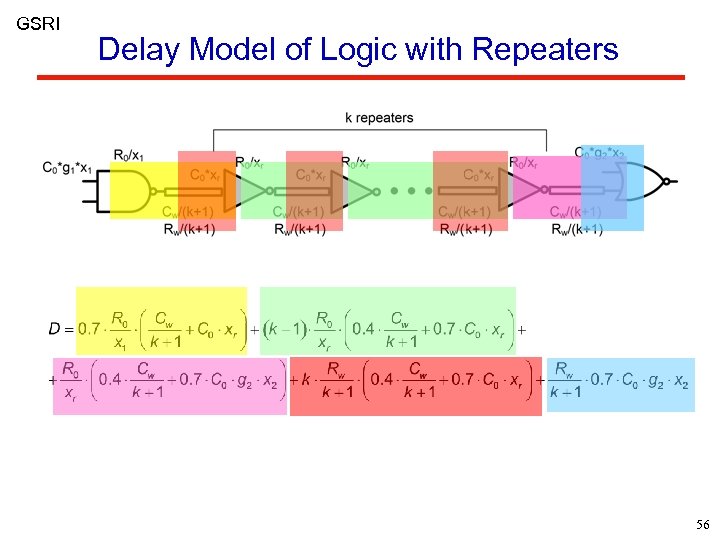GSRI Delay Model of Logic with Repeaters 56

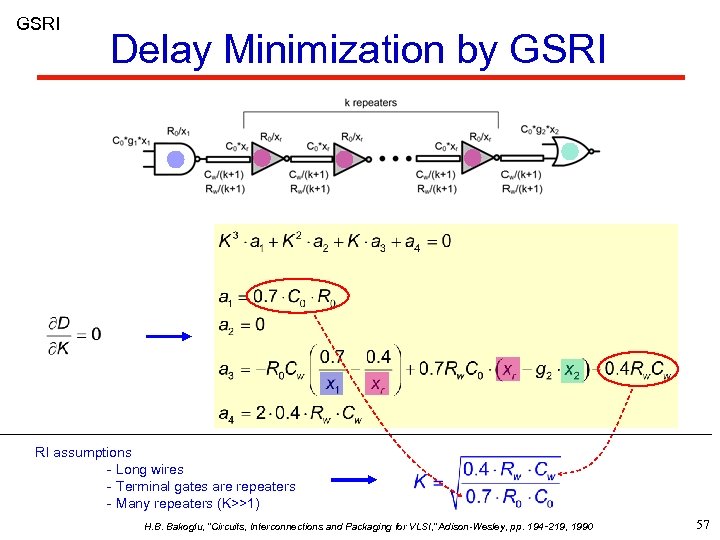GSRI Delay Minimization by GSRI RI assumptions - Long wires - Terminal gates are repeaters - Many repeaters (K>>1) H. B. Bakoglu, “Circuits, Interconnections and Packaging for VLSI, ” Adison-Wesley, pp. 194‑ 219, 1990 57

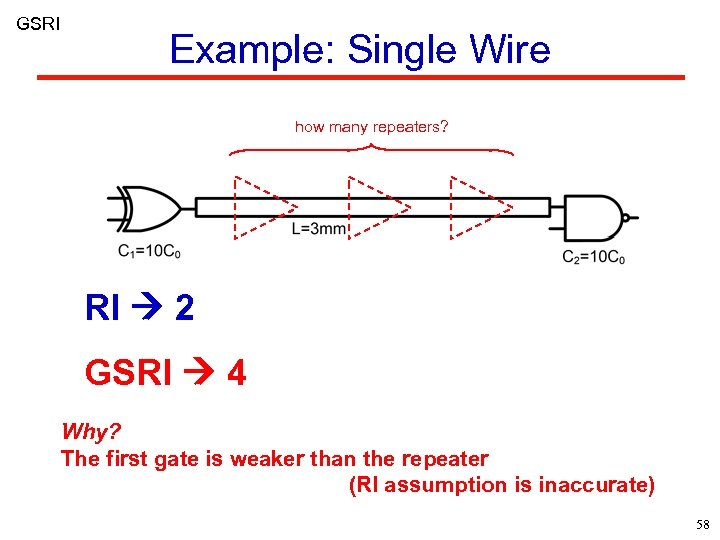GSRI Example: Single Wire how many repeaters? RI 2 GSRI 4 Why? The first gate is weaker than the repeater (RI assumption is inaccurate) 58

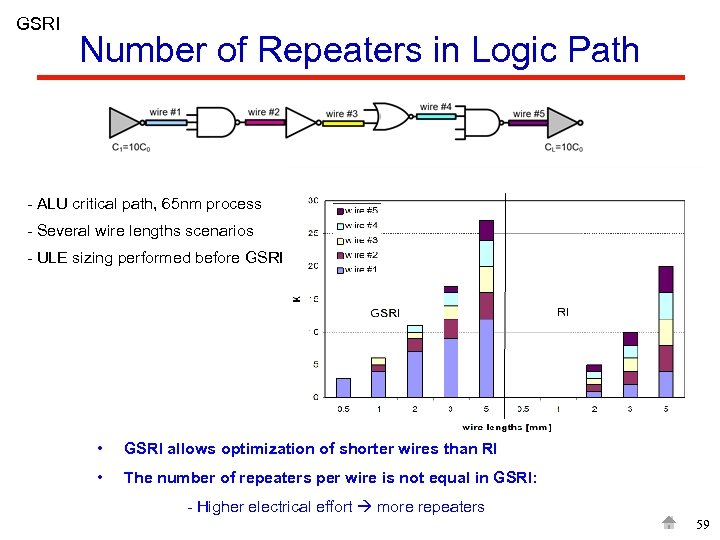GSRI Number of Repeaters in Logic Path - ALU critical path, 65 nm process - Several wire lengths scenarios - ULE sizing performed before GSRI • GSRI allows optimization of shorter wires than RI • The number of repeaters per wire is not equal in GSRI: - Higher electrical effort more repeaters 59

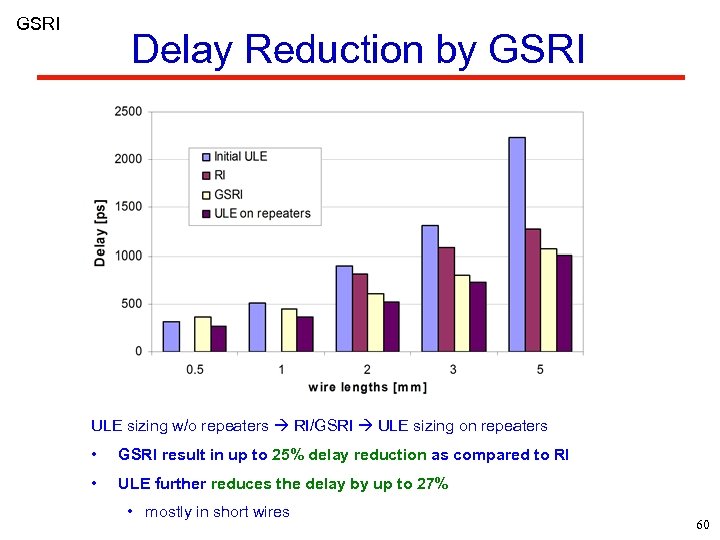GSRI Delay Reduction by GSRI ULE sizing w/o repeaters RI/GSRI ULE sizing on repeaters • GSRI result in up to 25% delay reduction as compared to RI • ULE further reduces the delay by up to 27% • mostly in short wires 60

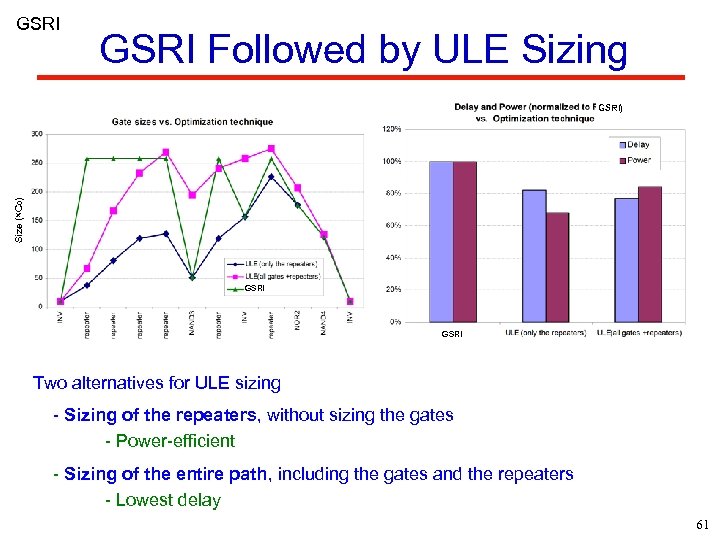GSRI Followed by ULE Sizing Size (×C 0) GSRI Two alternatives for ULE sizing - Sizing of the repeaters, without sizing the gates - Power-efficient - Sizing of the entire path, including the gates and the repeaters - Lowest delay 61

GSRI Delay [ps] Power [p. W] Using Smaller Repeaters 17% delay reduction & 15% power reduction • Smaller size more repeaters • Power may decrease for higher number of smaller repeaters Many smaller repeaters reduced transition time lower short-circuit currents 62

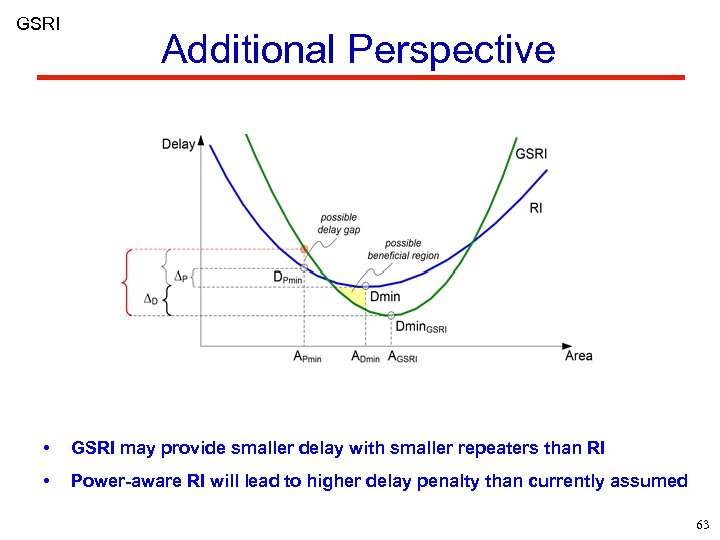GSRI Additional Perspective • GSRI may provide smaller delay with smaller repeaters than RI • Power-aware RI will lead to higher delay penalty than currently assumed 63

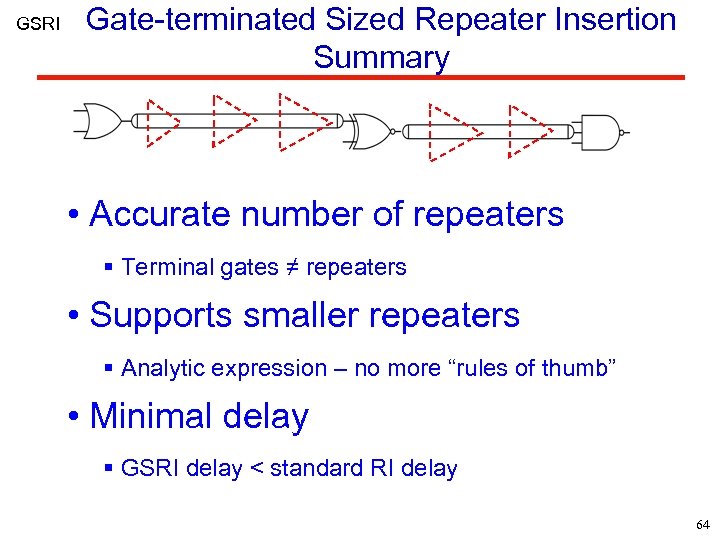GSRI Gate-terminated Sized Repeater Insertion Summary • Accurate number of repeaters § Terminal gates ≠ repeaters • Supports smaller repeaters § Analytic expression – no more “rules of thumb” • Minimal delay § GSRI delay < standard RI delay 64

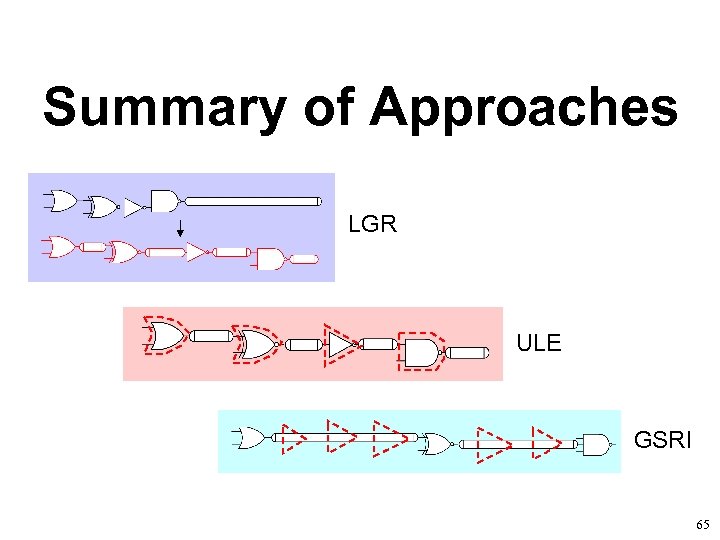Summary of Approaches LGR ULE GSRI 65

Summary LE – only logic RI – only wires We propose: general solution - logic with wires Unified Logical Effort (ULE) - Fast sizing of gates in presence of interconnect - Intuitive conditions for minimal delay Gate-terminated Sized Repeater Insertion (GSRI) - Accurate optimal number of repeaters - Enhanced design flexibility and smaller delay than in RI Logic Gates as Repeaters (LGR) - Distribution of logic gates over interconnect - Delay optimization without logically-redundant repeaters 66

Future Work Analyzing wire sizing Developing power efficient heuristics Incorporating inductance Integration in EDA tools 67

68