Time Value of Money —One dollar today is

Time Value of Money --One dollar today is of more value than one dollar in the future. Or: --To get my dollar today, you must give me more than one dollar in the future. Interest

Present Value • Present Value – The value today of a certain sum you will receive in the future. Depends on: • How far in the future • Interest Rate

Present Value • What is the present value of $100 paid in five years discounted at 10 percent Today 1 2 3 4 Future Discount at 10% PV=$62. 09 $100

Future Value • Future Value – A given sum invested today will grow to what value in the future? Also depends on: • How far in the future • Interest Rate

Future Value • What will the value be in five years of $62. 09 invested today at 10% interest. Today 1 2 3 4 Future Compound at 10% $62. 09 FV=$100. 00

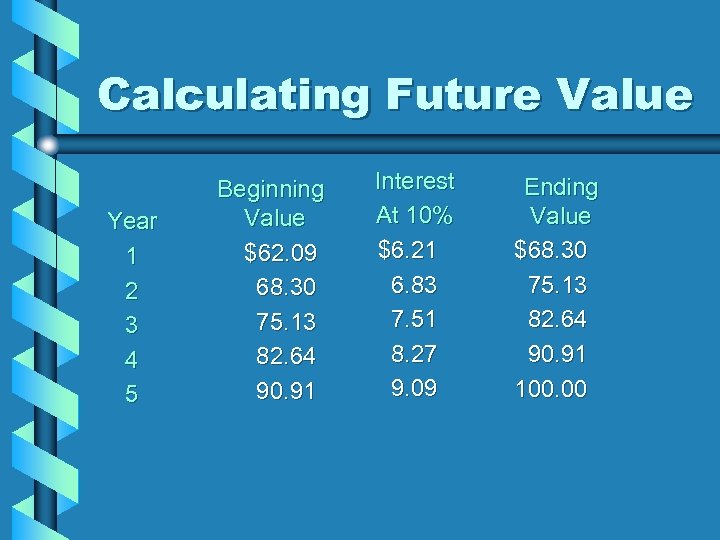Calculating Future Value Year 1 2 3 4 5 Beginning Value $62. 09 68. 30 75. 13 82. 64 90. 91 Interest At 10% $6. 21 6. 83 7. 51 8. 27 9. 09 Ending Value $68. 30 75. 13 82. 64 90. 91 100. 00

Calculating Future Value FV = p · (1 + i) · (1 + i) = p · (1 + i)5 or more generally = p · (1 + i)n Were: p = principal i = interest rate per year (period) n = number of years (periods)

Calculating Future Value From our example: FV = p · (1 + i)n = $62. 09 · (1 + 10%)5 = $62. 09 · (1. 1)5 = $62. 09 · 1. 61051 = $100. 00

Calculating Future Value From our example: FV = p · (1 + i)n = $62. 09 · (1 + 10%)5 = $62. 09 · (1. 1)5 = $62. 09 · 1. 61051 = $100. 00 Note the multiplier! See page C-4

Double Your Money!!! Quick! How long does it take to double $5, 000 at a compound rate of 12% per year (approx. )? We will use the “Rule-of-72”.

The “Rule-of-72” Quick! How long does it take to double $5, 000 at a compound rate of 12% per year (approx. )? Approx. Years to Double = 72 / i% 72 / 12% = 6 Years [Actual Time is 6. 12 Years]

Present Value Calculation Present Value of a single sum is discounting the Future Value back to the present at a certain interest (discount) rate. It’s given by the formula: PV = FV/(1 + i)n (See page C 9)

Present Value Calculation From our example: PV = FV / (1 + i)n = $100. 00 / (1 + 10%)5 = $100. 00 · [1 / (1. 1)5] = $100. 00 · 0. 62092 = $62. 09 Note the multiplier! See page C-8

Annuities • An annuity is a series of equal dollar flows (either paid or received). Examples include your car or house payments, equal deposits made to a savings account, interest payments on bonds.

Future Value of an Ordinary Annuity If one saves $1, 000 a year at the end of every year for three years in an account earning 8% interest, compounded annually, how much will one have at the end of the third year?

Example of an Ordinary Annuity – Future Value 0 1 End of Year 2 3 $1, 000 $1, 080 $1, 166 8% $1, 000 $3, 246 FVA 3 = 1, 000(1. 08)2 + 1, 000(1. 08)1 + 1, 000(1. 09)0 = $3, 246 4

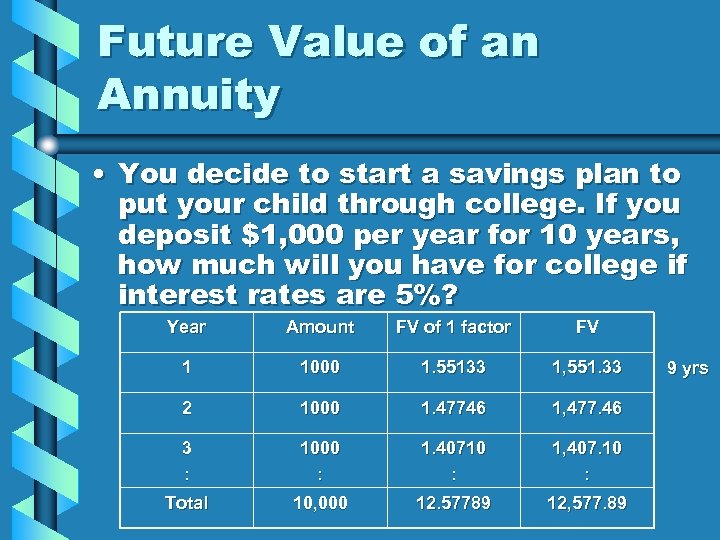Future Value of an Annuity • You decide to start a savings plan to put your child through college. If you deposit $1, 000 per year for 10 years, how much will you have for college if interest rates are 5%? Year Amount FV of 1 factor FV 1 1000 1. 55133 1, 551. 33 2 1000 1. 47746 1, 477. 46 3 : 1000 : 1. 40710 : 1, 407. 10 : Total 10, 000 12. 57789 12, 577. 89 9 yrs

Present Value of an Annuity Present Value of an annuity is the sum of the Present Values of each of the payments. (See page C 11)

Present Value of an Annuity -- Example • You win the $1, 000 lottery and the state promises to pay you $50, 000 per year for 20 years. What’s the real value of your winnings if interest rates are 5%? From the table on pg. C 11: PV factor for an Annuity = 12. 46221 Present Value = $50, 000 * 12. 46221 = $623, 110. 50

Present Value: Multiple Cash Flows Suppose an investment promises a cash flow of $500 in one year, $600 at the end of two years and $10, 700 at the end of the third year. If the discount rate is 5%, what is the value of this investment today? 0 5% 1 $500 PV 0 2 3 $600 $10, 700

Present Value: Multiple Cash Flows 0 1 5% $500 2 3 $600 $10, 700 $476. 19 $544. 22 $9, 243. 06 $10, 263. 47 = PV

Discounting Cash Flows All investment opportunities have an initial cost or other expected outlays associated with an investment. Investment opportunity Cash Outflows

Example: Cash Outflows Cash Outflow PV PV of Cash Factor Outflows Initial Cash Outlay $20, 000 1. 0000 $20, 000 Future cash outlay Total present value of cash outflows $ 5, 000 . 62092 $ 3, 105 $ 23, 105

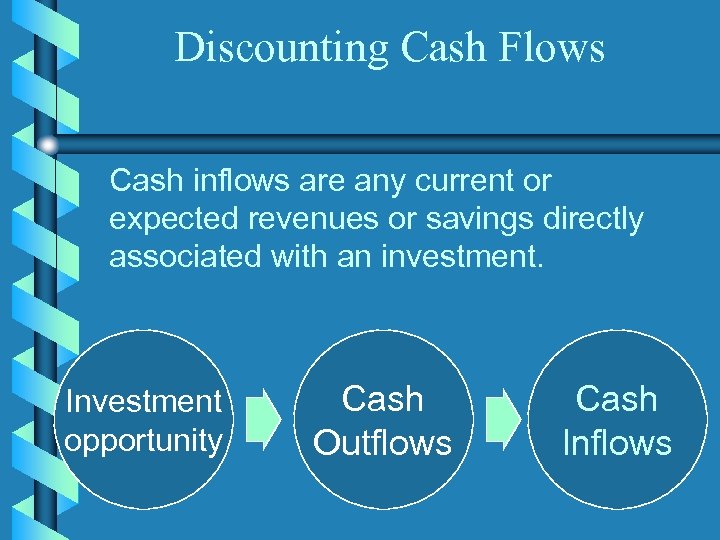Discounting Cash Flows Cash inflows are any current or expected revenues or savings directly associated with an investment. Investment opportunity Cash Outflows Cash Inflows

Example: Cash Inflows Assume the investment earns $3, 000/yr. for 10 years. Interest rates are 5%. Cash Inflow PV Factor PV of Cash Inflow Revenues $3, 000 7. 72173 $23, 165 Salvage Value Total present value of cash inflows $5, 000 0. 61391 $ 3, 070 $26, 235

Discounting Cash Flows If the present value of the cash inflows is greater than the present value of the cash outflows, you would be better off by making the investment than not. Present value of cash outflows Present value of cash inflows $ 23, 105 $ 26, 235

Discounting Cash Flows Conclusion: Present value of cash outflows Present value of cash inflows $ 23, 105 $ 26, 235 If this investment is accepted, we would expect to earn the required 5% on our money, plus we would be $ 3, 130 better off.

Bond Valuation Problem Find today’s value of a coupon bond with a maturity value of $1, 000 and a coupon rate of 6%. The bond will mature exactly ten years from today, and interest is paid semi-annually. Assume the discount rate used to value the bond is 8. 0% because that is now the market rate of return on an investment such as this. Interest = $30 every six months for 20 periods Interest rate = 8%/2 = 4% every six months

Bond Valuation Problem Find today’s value of a coupon bond with a maturity value of $1, 000 and a coupon rate of 6%. The bond will mature exactly ten years from today, and interest is paid semi-annually. Assume the discount rate used to value the bond is 8. 0% because that is now the market rate of return on an investment such as this. 30 30 30 30 30 1000

Bond Valuation Problem Add: 13. 59033 x 30 PV = $407. 71 Present Value of an annuity (n=20, pmt=30, i=4%) Present Value of a single sum . 45639 x 1000 PV = $456. 39 (FV=1000, n=20, i=4%) Bond value @ 8% discount 30 30 30 30 30 $864. 10 30 30 30 1000

Bond Valuation Problem Find today’s value of a coupon bond with a maturity value of $1, 000 and a coupon rate of 6%. The bond will mature exactly ten years from today, and interest is paid semi-annually. Assume the discount rate used to value the bond is 6. 0% because that is now the market rate of return on an investment such as this.

Bond Valuation Problem Add: 14. 87747 x 30 PV = $446. 32 Present Value of an annuity (n=20, pmt=30, i=3%) Present Value of a single sum . 45639 x 1000 PV = $553. 68 (FV=1000, n=20, i=3%) Bond value @ 6% discount 30 30 30 30 30 $1, 000. 00 30 30 30 1000

Bond Valuation Problem Find today’s value of a coupon bond with a maturity value of $1, 000 and a coupon rate of 6%. The bond will mature exactly ten years from today, and interest is paid semi-annually. Assume the discount rate used to value the bond is 4. 0% because that is now the market rate of return on an investment such as this.

Bond Valuation Problem Add: 14. 87747 x 30 PV = $490. 54 Present Value of an annuity (n=20, pmt=30, i=2%) Present Value of a single sum . 45639 x 1000 PV = $672. 97 (FV=1000, n=20, i=2%) Bond value @ 4% discount 30 30 30 30 30 $1, 163. 51 30 30 30 1000

Bond Valuation Problem Notice, there is an inverse relationship! • As interest rates go the value goes • If interest rates go the value goes

Problem 1: You must decide between $25, 000 in cash today or $30, 000 in cash to be received two years from now. If you can earn 8% interest on your investments, what is the present value of each, and which is the better deal? PV of $25, 000 today = $25, 000. 00 PV of $30, 000 in 2 yrs = $25, 720. 16

Problem 2: You plan to invest $100 per year four years, with the first cash flow one year from today, earning 5% interest compounded annually. Your investment will be worth how much four years from today. FV of an annuity of $100, 4 periods, 5% 4. 31013 * 100 = $431. 01