Time Value 1 Time Value What

Time Value 1

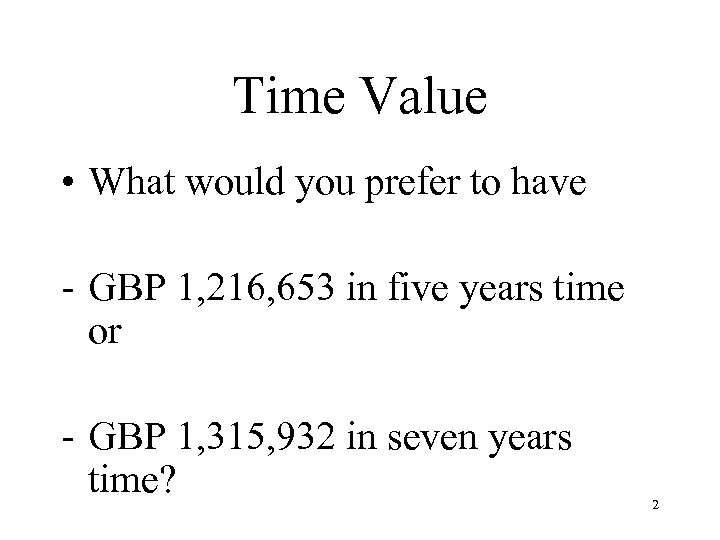Time Value • What would you prefer to have - GBP 1, 216, 653 in five years time or - GBP 1, 315, 932 in seven years time? 2

Time Value (Future Value) • Compounding, interest earned in one period is added to the principal to work out interest for the next period. (It is assumed you do not spend it!) 3

Time Value (Future Value) • Take an example of GBP 1, 000 invested at 4% for 5 years Year 1 1, 000 x. 04 = 40, 000 Year 2 1, 040, 000 x. 04 = 41, 600 We could go on but it is boring 4

Time Value (Future Value) • Luckily we are able to generalise the step by step approach. • Note at the end of year two the total value (Future Value) is 1, 081, 600 (1, 040, 000 + 41, 600). • We may get the same result by multiplying today’s principal amount (present value or Po) by (1+. 04) • 1, 000 x 1. 0816 • So FV = Po x (1. 04)2 Try 5 years. = 1. 21665 (1. 2167) 5

Time Value (Future Value) • (1. 04)5 = 1. 216652902 • Therefore the future value of GBP 1, 000 compounded at 4% per annum will be GBP 1, 216, 653 6

Time Value (Present Value) • Return to our initial question, ‘which would you prefer, GBP 1, 216, 653 in five years or GBP 1, 315, 932 in seven years? ’ • Our problem is that different amounts at different times are not comparable directly. • Different amounts are comparable today. • We know that at an interest rate of 4% 1, 216, 653 in five years has a value today of 1, 000. This is referred to as the present value. 7

Time Value (Present Value) • 1, 000 x (1. 04)5 = 1, 216, 653 • 1, 000 x 1. 216653 = 1, 216, 653 Therefore the present value may be found • 1, 216, 653 = 1, 000 1. 216653 8

Time Value (Present Value) • So all we need do is discount 1, 315, 932 at 4% for 7 years and see if it gives a present value of more or less than 1, 000. • (1. 04)7 = 1. 315932 • 1, 315, 932 = 1, 000 1. 315932 Note the above is the same as 1, 315, 932 x 1 = 1, 315, 932 x. 759917686 1. 315932 = 1, 000 9

Time Value Annuities • An Annuity is an ‘investment that pays a predetermined annual (or other time period i. e. monthly) regular income. The amounts are always the same. • Annuities also have present values and future values. 10

Time Value Annuities Future Value • Suppose you have an annuity of GBP 1, 000 per annum for three years. Payment is made at year end. Payment at No of Yrs FV at 5% End Value end year interest 1. 1, 000 2 1. 1025 1, 102. 5 2. 1, 000 1 1. 05 1, 050. 0 3. 1, 000 0 1, 000. 0 3, 152. 5 11

Time Value Annuities Present Value • As with uneven flows we may use tables of factors to find future values and to produce present values • What investment is needed today to produce an annuity of 1, 000 p. a. for three years at 5%? • 1, 000 x pv annuity factor • 1, 000 x 2. 7232 = 2, 723. 2 12

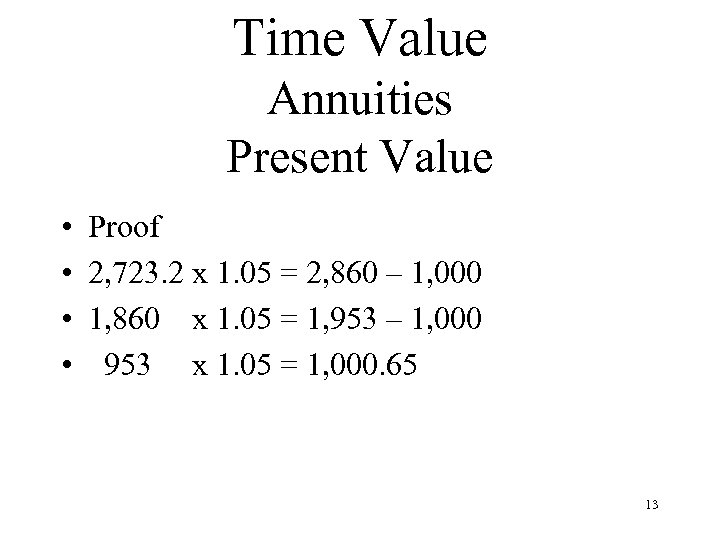Time Value Annuities Present Value • • Proof 2, 723. 2 x 1. 05 = 2, 860 – 1, 000 1, 860 x 1. 05 = 1, 953 – 1, 000 953 x 1. 05 = 1, 000. 65 13

Time Value Annuities • We use annuities where the flows are of the same amount. • As individuals we come across them most frequently with Mortgages but also • Purchasing annuities on retirement • Some loan repayments 14

Time Value Annuities • Example. • You wish to borrow GBP 500, 000 to buy a one bed room flat in Bath. • Mortgage at 5% repaid over 4 years by 4 annual payments • 500, 000 = 141, 004 3. 5460 (PVAn Factor) 15

Time Value Annuities • Example • A benefactor wishes to reward your first class degree in four years time with a gift of GBP 1, 000. How much will they need to invest annually to produce this sum at an interest rate of 4%? • 1, 000 = 235 4. 2465 16

Time Value Annuities/Bonds • Bonds Definition A Bond is a negotiable certificate that evidences indebtedness. Bonds are also referred to as ‘notes’ or ‘debentures’ With a fixed interest rate bond you receive a fixed set of cash flows representing the interest (coupon) flows plus a final cash flow of principal. 17

Time Value Bonds • A bond is issued at par with a face value of USD 100, 0000 at 10%, interest paid annually, repayment in three years. 18

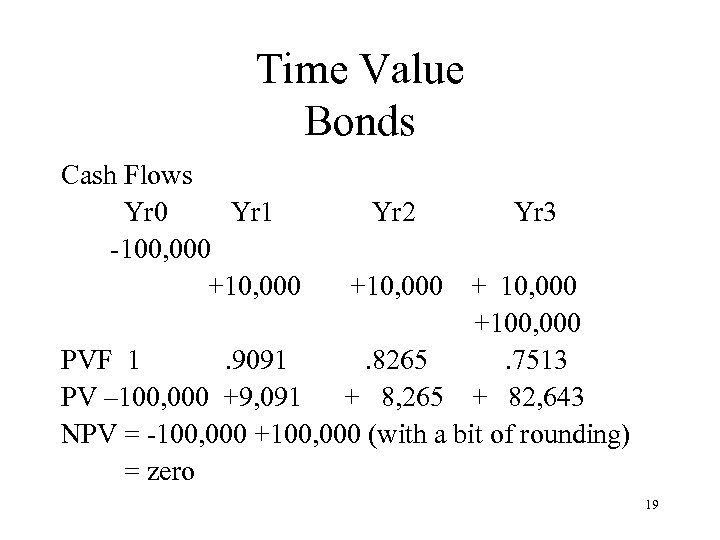Time Value Bonds Cash Flows Yr 0 Yr 1 -100, 000 +10, 000 Yr 2 Yr 3 +10, 000 +100, 000 PVF 1. 9091. 8265. 7513 PV – 100, 000 +9, 091 + 8, 265 + 82, 643 NPV = -100, 000 +100, 000 (with a bit of rounding) = zero 19

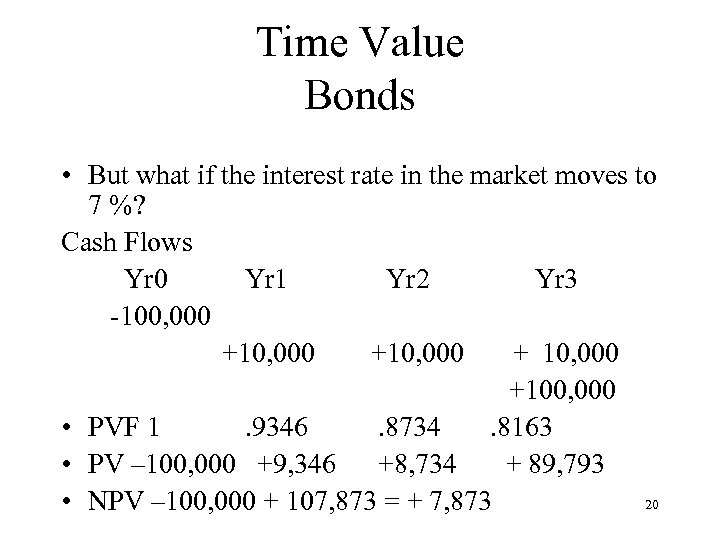Time Value Bonds • But what if the interest rate in the market moves to 7 %? Cash Flows Yr 0 Yr 1 Yr 2 Yr 3 -100, 000 +10, 000 +100, 000 • PVF 1. 9346. 8734. 8163 • PV – 100, 000 +9, 346 +8, 734 + 89, 793 20 • NPV – 100, 000 + 107, 873 = + 7, 873

Time Value APR • Annual Percentage Rate or Effective Rate • You are charged by your credit card supplier at a rate of 6 % per annum, monthly. • What is this on an annual basis? • 12 • - 1 x 100 = 6. 16 % 1+. 06 12 21

Time Value • • • Real and Nominal rates If you are offered a rate of return of 10% pa but inflation is at 5% then your real rate, i. e. your increased purchasing power is 4. 762 % Cost of product GBP 10 Price after one year 10 x 1. 05 = GBP 10. 5 Return on GBP 10 after one year 10 x 1. 1= 11 Purchasing power = 11 = 1. 047619 or 4. 762% 10. 5 22

Time Value • To obtain a real rate of 5% when inflation is 5 % then the nominal rate must be (1. 05 x 1. 05) -1 x 100 = 10. 25 Test 10 x 1. 1025 = 11. 025 = 1. 05 10 x 1. 05 = 10. 5 23