Time Complexity Measuring Complexity Worst-case analysis

Time Complexity

Measuring Complexity Worst-case analysis Average-case analysis Define M: a det. Turing machine that halts on all input The running time or time complexity of M is the function f: N N, where f(n) is the maximum number of steps that M uses on any input of length n If f(n) is the running time of M, we say M runs in time f(n) and that M is an f(n) time Turing machine. p 2.

Big-O and small-o Notation Def: p 3.

Complexity relationships among models p 4.

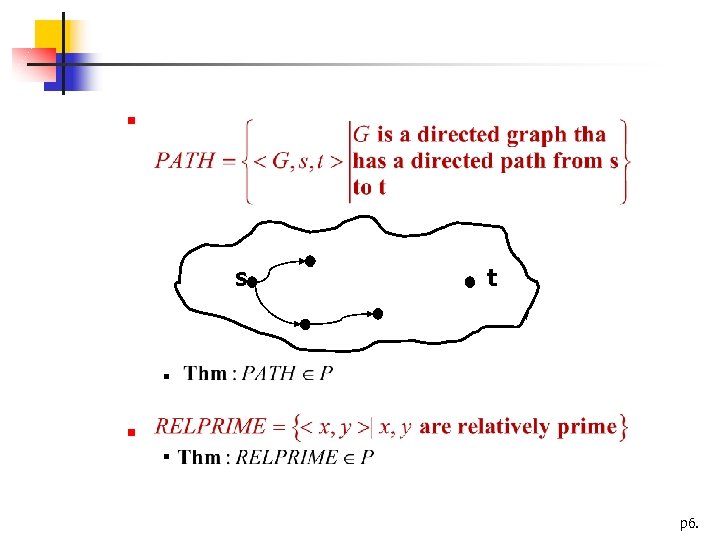
The class P P is the class of languages that are decidable in polynomial time on a deterministic singletape TM In other words, p 5.

s t p 6.

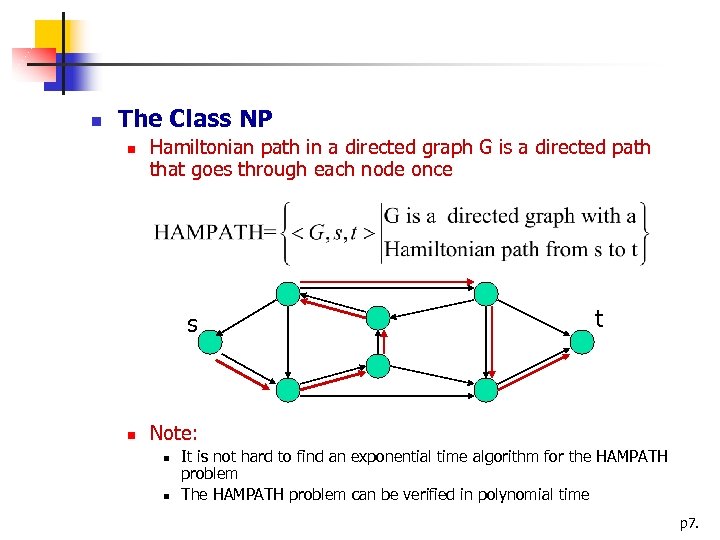The Class NP Hamiltonian path in a directed graph G is a directed path that goes through each node once s t Note: It is not hard to find an exponential time algorithm for the HAMPATH problem The HAMPATH problem can be verified in polynomial time p 7.

12653 = 123 x 111 verifiable in poly. time Not all problem can be verified in poly. time. Def: A verifier for a language A is an algorithm V, where A = { | V accepts < , c> for some string c} A polynomial time verifier runs in polynomial time in the length of A language A is polynomially verifiable if it has a polynomial time verifier. A verifier uses additional information c to verify that a string is member of A C: certificate or proof of membership in A p 8.

Def: NP is the class of languages that have polynomial time verifiers NP: Non-deterministic Polynomial time Def: Thm: A language is in NP iff it is decided by some nondeterministic polynomial time Turing machine Pf: p 9.

p 10.

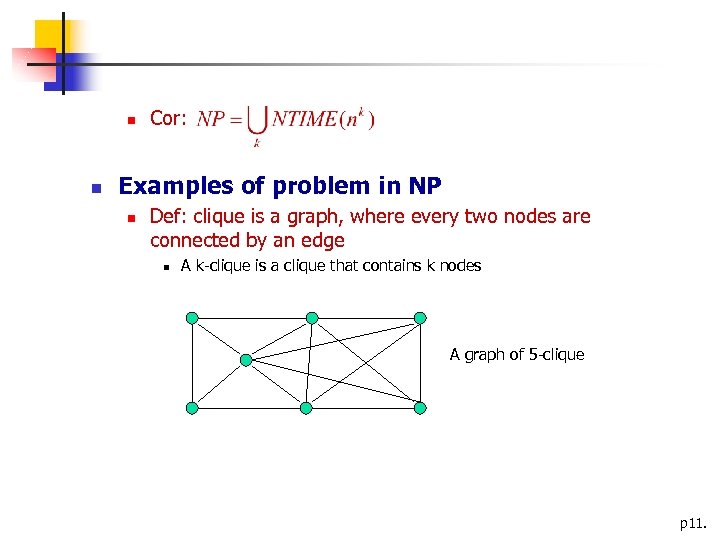Cor: Examples of problem in NP Def: clique is a graph, where every two nodes are connected by an edge A k-clique is a clique that contains k nodes A graph of 5 -clique p 11.

Def: Thm: CLIQUE is in NP pf : p 12.

Def: Thm: SUBSET-SUM is in NP Pf: p 13.

P = the class of languages where membership can be decided quickly NP= the class of languages where membership can be verified quickly ? BIG Question!! P = NP p 14.

NP-completeness The satisfiability problem is to test whether a Boolean formula is satisfiable p 15.

Thm: Cook-Levin Theorem Def: p 16.

Def: A B p 17.

Thm: Pf: p 18.

Def: A language B is NP-complete if it satisfies two condition: 1. B is in NP 2. Every A in NP is polynomial time reducible to B (with only 2, it is called NP-hard) Thm: Pf: p 19.

Thm: Pf: p 20.

Def p 21.

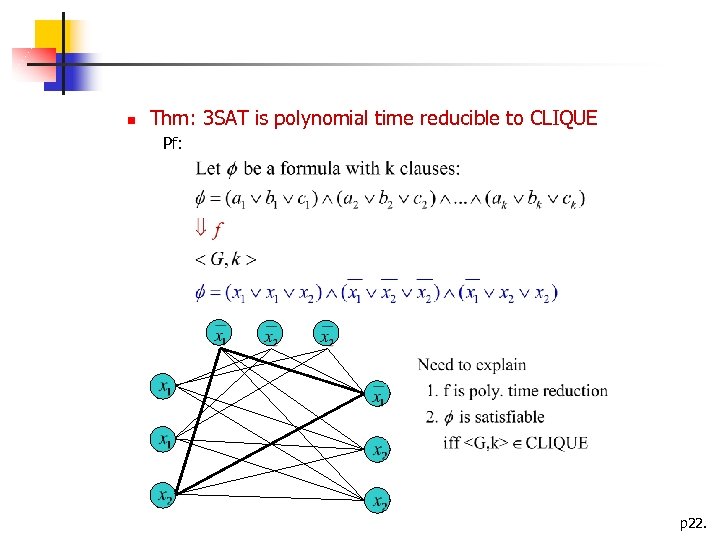Thm: 3 SAT is polynomial time reducible to CLIQUE Pf: p 22.

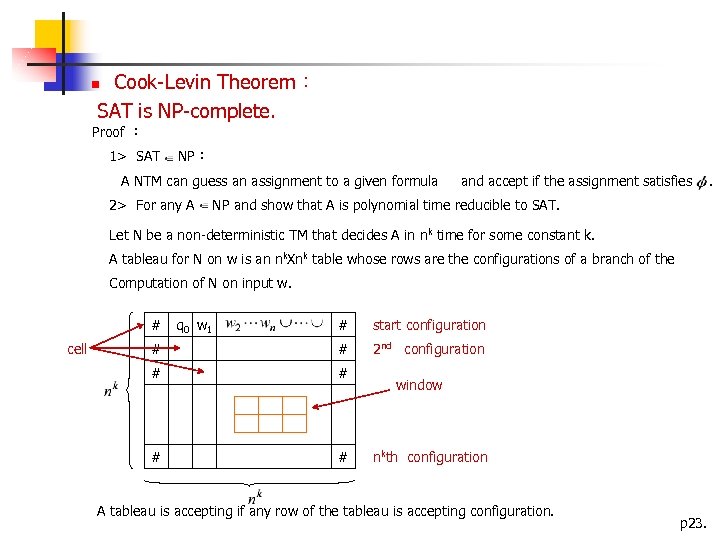Cook-Levin Theorem： SAT is NP-complete. Proof ： 1> SAT NP： A NTM can guess an assignment to a given formula 2> For any A and accept if the assignment satisfies NP and show that A is polynomial time reducible to SAT. Let N be a non-deterministic TM that decides A in nk time for some constant k. A tableau for N on w is an nk. Xnk table whose rows are the configurations of a branch of the Computation of N on input w. # cell q 0 w 1 # start configuration # # 2 nd configuration # # window nkth configuration A tableau is accepting if any row of the tableau is accepting configuration. p 23. .

Every accepting tableau for N on w corresponds to a computation branch of N on w. * Determine whether N accepts w is equivalent to determine whether an accepting tableau for N on w exists. f：polynomial time reduction from A to SAT. On input w, the reduction produces a formula Let Q and be the state set and the tape alphabet of N. Let If Design . For and each we have a variable such variables. , it means cell[i, j] contains an s. so that a satisfying assignment to the variable does correspond to an accepting tableau for N on w. (1) i s j

Ensure that the first row of the table is the starting configuration of N on w. (3) Guarantees that an accepting configuration occurs in the tableau. (4) This part is more complicated ! guarantee that each row of the table corresponds to a configuration that legally follows the preceding Row’s configuration according to N’s rules. a q 1 b a a c a a # b q 2 # b b q 2 a q 2 q 1 a (a) (d) # # b b a b c a a (b) a a q 1 b a q 2 (c) a a a q 1 a b legal windows (b) a a b q 2 (c) b c b b

Examples of illegal windows： (a) a a b a (b) a a a q 1 b q 1 a a (c) a q 1 a q 2 b q 2 Claim：If the top row of the table is the start configuration and every window in the table is legal, each row of the table is a configuration that legally follows the preceding one. a # b q 2 q 1 b a a # c a a # a is a legal window j a 1 a 2 a 3 j+1 a 4 a 5 a 6 i-1 i i+1 Size of ： Total number of variables Thus the reduction is poly.

Cor： 3 SAT is NP-complete. Proof ： 3 SAT is in NP. How about Cor： CLIQUE is NP-complete. p 27.

Vertex cover of G： If G is an undirected graph, a vertex cover of G is a subset of the nodes where every edge of G touches one of those nodes. 1 4 3 {2, 3} is a vertex cover. {1, 3} is not a vertex cover. VERTEX-COVER={|G is an undirected graph that has a k-node vertex cover}. p 28.

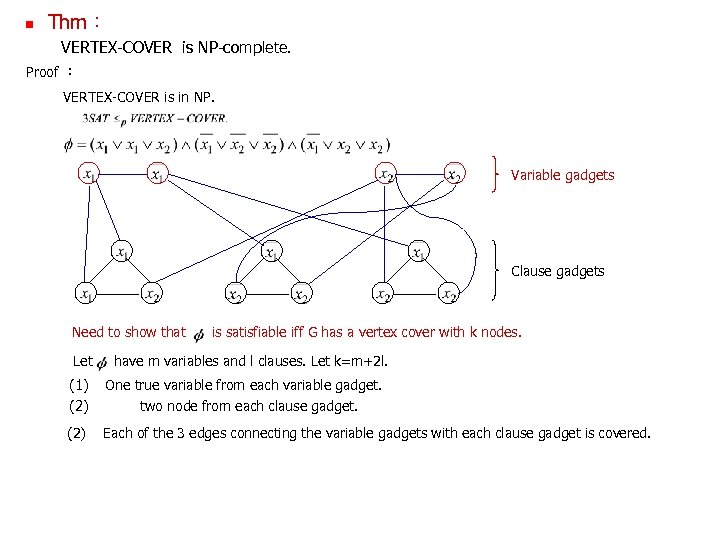Thm： VERTEX-COVER is NP-complete. Proof ： VERTEX-COVER is in NP. Variable gadgets Clause gadgets Need to show that Let is satisfiable iff G has a vertex cover with k nodes. have m variables and l clauses. Let k=m+2 l. (1) (2) One true variable from each variable gadget. two node from each clause gadget. (2) Each of the 3 edges connecting the variable gadgets with each clause gadget is covered.

SUBSET-SUM： p 30.

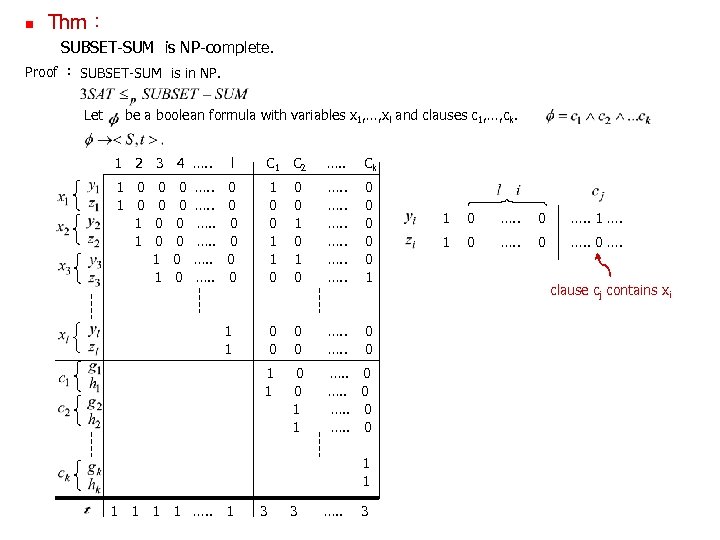Thm： SUBSET-SUM is NP-complete. Proof ： SUBSET-SUM is in NP. Let be a boolean formula with variables x 1, …, xl and clauses c 1, …, ck. 1 2 3 4 …. . l C 1 C 2 …. . Ck 1 0 0 1 0 1 1 0 0 0 1 0 …. . 0 0 0 1 1 1 0 0 …. . 0 0 1 1 …. . 0 0 0 0 0 …. . 1 1 1 …. . 1 3 3 …. . 3 1 0 …. . 1 …. 1 0 …. clause cj contains xi

(1) Suppose is satisfiable. Construct a subset S as follows. If xi is assigned TRUE, select yi else select zi. I. e. for each I, we select either yi or zi. Last k digits add up between 1 and 3. Select enough of g and h numbers to make each of the last k digits up to 3. (2) Suppose a subset of S sums to t. We construct a satisfying assignment to . If the subset contains yi , we assigned xi TRUE else assign xi FALSE. This assignment satisfied The table has size ! Why? ?

MAX-SAT: Given a boolean formula , and an integer k, is there a truth assignment that satisfies at least k clauses? Thm: MAX-SAT is NP-complete Pf: SAT p MAX-SAT = c 1 c 2 … cm k=m Thm: DOUBLE-SAT: Given a boolean formula , are there at least 2 truth assignment for ? DOUBLE-SAT is NP-complete p 33.

Def: Hamiltonian path in a directed graph G is a directed path that goes through each node once. HAMPATH: Given a directed graph and its 2 vertices s and t, is there a Hamiltonian path from s to t? Thm: HAMPATH is NP-complete Pf: (long…later) 3 SAT p HAMPATH UHAMPATH: Given a undirected graph and its 2 vertices s and t, is there a Hamiltonian path from s to t? p 34.

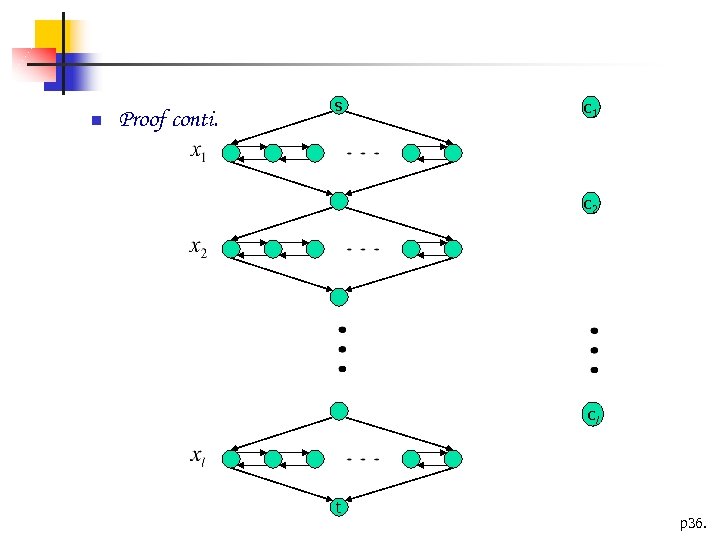
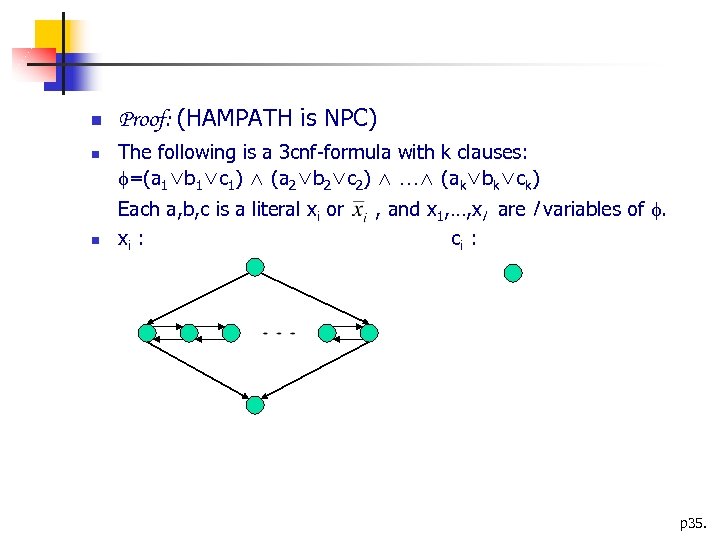Proof: (HAMPATH is NPC) The following is a 3 cnf-formula with k clauses: =(a 1∨b 1∨c 1) ∧ (a 2∨b 2∨c 2) ∧ …∧ (ak∨bk∨ck) Each a, b, c is a literal xi or xi : , and x 1, …, xl are l variables of . ci : p 35.

Proof conti. s c 1 c 2 cl t p 36.

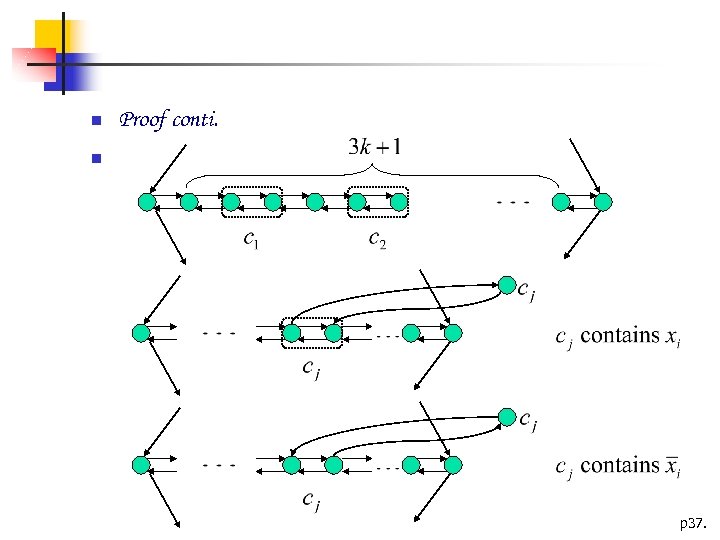
Proof conti. p 37.

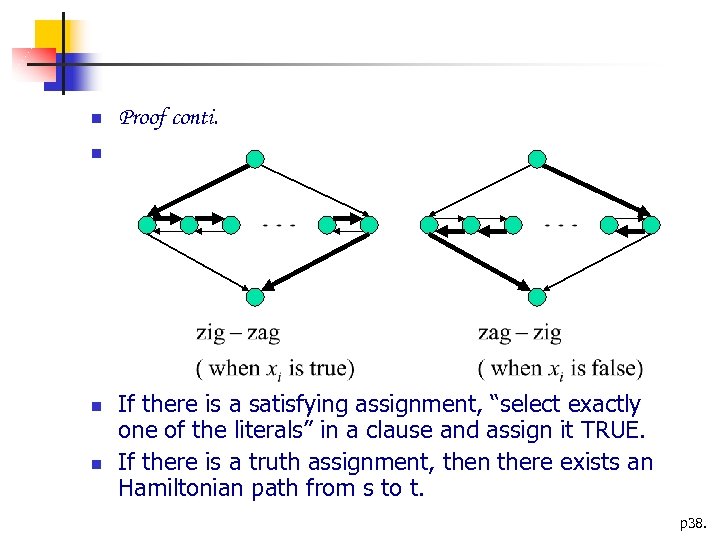Proof conti. If there is a satisfying assignment, “select exactly one of the literals” in a clause and assign it TRUE. If there is a truth assignment, then there exists an Hamiltonian path from s to t. p 38.

Proof conti. If the Hamiltonian path is normal, that is, it goes through the diamonds in order from the top one to the bottom one, we can easily get the satisfying assignment. Because each clause node appears on the path, by observing the diamond at which the detour to it is taken, we may determine which of the literals in the corresponding clause is TRUE. If the path zigzag, we assign corresponding variable TRUE If the path zagzig, we assign FALSE. p 39.

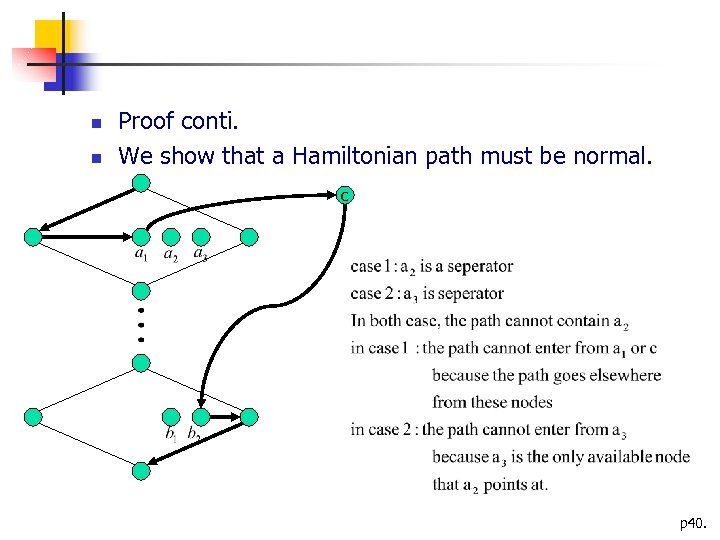Proof conti. We show that a Hamiltonian path must be normal. c p 40.

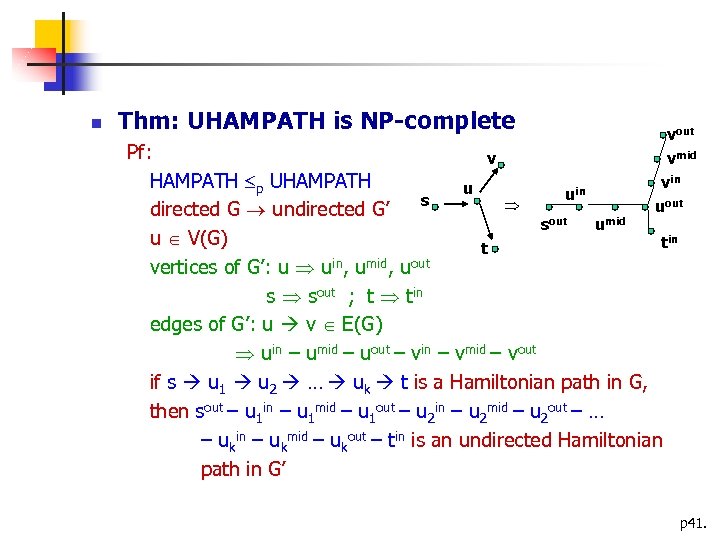Thm: UHAMPATH is NP-complete vout vmid vin uout Pf: v HAMPATH p UHAMPATH u uin s directed G undirected G’ sout umid u V(G) tin t vertices of G’: u uin, umid, uout s sout ; t tin edges of G’: u v E(G) uin – umid – uout – vin – vmid – vout if s u 1 u 2 … uk t is a Hamiltonian path in G, then sout – u 1 in – u 1 mid – u 1 out – u 2 in – u 2 mid – u 2 out – … – ukin – ukmid – ukout – tin is an undirected Hamiltonian path in G’ p 41.

Undirected Hamiltonian Cycle Thm: Undirected Hamiltonian Cycle is NP-comlplete Pf: UHAMPATH p UHAMCYCLE Traveling Salesman Problem: (TSP) Given an integer n 2, an n n distance matrix of some cities, and an integer B 0, is there a tour that visits every city exactly once and returns to the starting city by traveling within distance B? Thm: TSP is NP-complete Pf: UHAMCYCLE p TSP p 42.

Longest Cycle: Given a graph and integer k, is there a cycle, with no repeated nodes, of length at least k? Thm: LONGEST CYCLE is NP-complete SUBGRAPH ISOMORPHISM: Given 2 undirected graphs G and H, is G a subgraph of H? Thm: SUBGRAPH ISOMORPHISM is NP-complete p 43.

Coping with NP-completeness: Approximation algorithms: Let x be an instance of an optimization problem Opt(x): the optimum solution of x A: a poly. time algorithm for x : positive real number If A satisfies For all x, then we say A is an -approximation algorithm p 44.

Eg. The following is a 1 -approximation algorithm for the vertex cover problem. 4 C={2, 3} G: 2 3 1 Algorithm: 1. C : = ; 2. while there is an edge [u, v] in G add u, v to C and delete them from G Let be the optimum vertex cover c={ , , , …, } p 45.

Polynomial Time Approximation Scheme(PTAS) We say that an approximation scheme is PTAS, if for any fixed >0, the scheme runs in time polynomial in the size n of its input instance. Ratio bound: Inapproximable problem: If there is no -approximation algorithm for them with however large , unless P=NP p 46.

Thm: TSP is inapproximable unless P=NP Pf: Let G be a graph with n nodes. UHAMCYCLE p TSP If G has a Hamiltonian cycle, then the optimum cost of a tour is n; otherwise if G has no Hamiltonian cycle, then the optimum cost of a tour > n(1+ ) 1 2+3 1 p 47.

If TSP had an -approximation algorithm A, then we would be able to tell whether G has a Hamiltonian cycle. Run A for TSP: i> if the returned cost n(1+ )+1: No cycle ii> if the returned cost n(1+ ): has a cycle Unless P=NP, TSP is inapproximable. p 48.

Backtracking and Branch&Bound: A={S 0} while A is not empty do choose a subproblem S and delete it from A choose a way of branching out of S , say to subproblems S 1, S 2, …, Sr for each subproblem Si in this list do if test(Si) returns “solution found” else if test(Si) returns “? ” then add Si to A Return “no solution” p 49.

Eg. x=T y=F x=F z=T z=F p 50.

Branch&Bound algorithm: A: ={S 0} , best_so_far: = while A is not empty do choose a subproblem S and delete it from A choose a way of branching out of S , say to subproblems S 1, S 2, …, Sr for each subproblem Si in this list do if |Si|=1 then update best_so_far else if lowerbound(Si) < best_so_far then add Si to A Return best_so_far p 51.

Local improvement algorithm: S= initial solution while there is a solution S’ such that S’ is a neighbor of S and cost(S’) < cost(S) do S: =S’ Return S p 52.

Simulated annealing: S= initial solution; T: =T 0 repeat generate a random solution S’ such that S’ is a neighbor of S and let = cost(S’) cost(S) if 0 then S: =S’ else S: =S’ with probability e- /T update (T) until T=0 Return the best solution seen! T: temperature p 53.